年金的终值和现值

与单笔现金流量相比，系列现金流量是指在一定时期内会产生多笔现金流量，根据每次现金流量是否相等，可以分为等额系列现金流量与非等额系列现金流量。等额系列现金流量又称年金，其特点是，在一定时期内每隔相同的时间 （可以不是一年）连续发生相等的现金流量。例如人们退休后所得到的养老金、分期付款赊购、分期偿还贷款、存本取息存款、债券分期付息、股票每年分红，等等。

按照现金流量发生的时点不同，年金可分为普通年金、预付年金、递延年金和永续年金等形式。

1.普通年金

普通年金是指从第一期起，每期期末发生等额现金流量的现金流系列。每一固定间隔期，有期初和期末两个时点，由于普通年金是在期末发生现金流入或流出，故又称后付年金。以后凡涉及年金问题，如不作特殊说明，均指普通年金。

1）普通年金终值的计算

如图2－5所示为n期普通年金，每期期末现金流量A的复利终值之和，即为普通年金的终值，计算公式为：

F＝A＋A（1＋i）1＋…＋A（1＋i）n－3＋A（1＋i）n－2＋A（1＋i）n－1

将上式整理可得：

公式 （2－4）中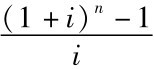，是年金A为1元、利率为i、期限为n的普通年金的终值，称为 “年金终值系数”，用符号表示为 （F／A，i，n），可通过直接查阅 “年金终值系数表”获得。例如，（F／A，10％，5）表示利率为10％的5期普通年金终值系数，查表可知该系数为61051。

图2－5 普通年金终值计算示意图

【例2－5】 小王是一位热心于公众事业的人，自1995年12月底开始，他每年都要向一位失学儿童捐款。小王向这位失学儿童每年捐款1000元，帮助其完成九年义务教育。假定每年定期存款利率为2％，则小王9年的捐款在2003年年底相当于多少钱？

分析：

小王1995—2003年每年年底捐款1000元，构成9期普通年金。

解：

F＝A（F／A，i，n）＝1000×（F／A，2％，9）＝1000×9.7546＝9754.6（元）

【例2－6】 某矿业公司决定将其西南部的一处矿产开采权公开拍卖，因此它向世界各国煤炭企业招标开矿。A公司和B公司的投标书最具有竞争力。A公司的投标书显示，该公司如取得开采权，从获得开采权的第1年开始，每年末向矿业公司交纳10亿美元的开采费，直到10年后开采结束。B公司的投标书表示，该公司在取得开采权时，直接付给矿业公司40亿美元，在8年后开采结束时，再付给60亿美元。如矿业公司要求的开矿年投资回报率达到15％，问该矿业公司应接受哪家公司的投标？

分析：

要解决上述问题，主要是比较两个公司给该矿业公司的开采权收入的大小。但由于两个公司支付开采权费用的时间不同，因此不能直接比较，而应比较这些支出在第10年终值的大小。试分析如下：

解：

A公司的方案对矿业公司来说是一笔年收款10亿美元的10年年金，其终值计算如下：

F＝A（F／A，i，n）＝10（F／A，15％，10）＝10×20.304＝203.04（亿美元）

B公司的方案对矿业公司来说是两笔收款，分别计算其终值，再求和：

第1笔收款（40亿美元）的终值＝40×（1＋15％）10＝40×4.0456＝161.824（亿美元）

第2笔收款（60亿美元）的终值＝60×（1＋15％）2＝60×1.3225＝79.35（亿美元）

合计终值241.174亿美元。

根据以上计算结果，矿业公司应接受B公司的投标。

【例2－7】 某人有一笔2年后到期的债务10万元，到期一次还清借款。为此他每月末向银行存一笔钱，年利率为12％，以备到期还债，问他每月应存多少元？

分析：

2年内每月末等额存款，构成普通年金，共24期，利率为12％／12＝1％，此题相当于已知终值10万元，求解年金A。

解：

F＝A（F／A，1％，24）

A＝F／（F／A，1％，24）＝100000／26.973＝3707.41（元）

例2－7的计算又称为偿债基金的计算，偿债基金是指为了在约定的未来某一时点清偿某笔债务或积聚一定数额的资金而必须分次等额形成的存款准备金。其本质就是已知F、i、n，解出年金A，这个A就是偿债基金。偿债基金和普通年金终值互为逆运算，其计算公式为：

公式（2－5）中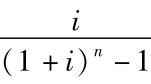，称为 “偿债基金系数”，用符号表示为 （A／F，i，n），该系数同普通年金终值系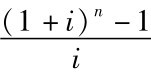数互为倒数。

在实际工作中，公司可能根据要求，在贷款期内建立偿债基金，以保证在期满时有足够的现金偿付贷款本金或兑现债券。

例如，一家公司在10年后要偿还面值为100万元的债券，假设利率为10％，那么，公司每年的偿债基金为：偿债基金A＝F／（F／A，10％，10）＝1000000／15.937＝62747（元）。

2）普通年金现值的计算

如图2－6所示，每期期末现金流量A的复利现值之和，即为普通年金的现值，计算公式为：

P＝A（1＋i）－1＋A（1＋i）－2＋A（1＋i）－3＋…＋A（1＋i）－（n－1）＋A×（1＋i）－n

将上式整理可得：

公式 （2－6）中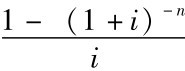，是年金A为1元、利率为i、期限为n的普通年金的现值，称为 “年金现值系数”，用符号表示为 （P／A，i，n），可通过直接查阅 “年金现值系数表”获得。

图2－6 普通年金现值计算示意图

【例2－8】 A公司以分期收款方式向Y公司出售一台大型设备。合同规定Y公司在10年内每半年支付5000元欠款。A公司为马上取得现金，将合同向银行折现。假设银行愿意以14％的利率、每半年计息一次的方式对合同金额进行折现。问A公司将获得多少现金？若折现率为8％，A公司将获得多少现金？

解：

年金A＝5000元，期数n＝20，i＝14％÷2＝7％

P＝A×（P／A，i，n）＝5000×（P／A，7％，20）＝5000×10.5940＝52970（元）

P＝A×（P／A，i，n）＝5000×（P／A，4％，20）＝5000×13.5903＝67951.5（元）

【例2－9】 某企业从银行取得1000万元的贷款，在10年内以年利率12％等额偿还，则每年应还的金额是多少？

分析：

此题相当于已知普通年金现值P、利率i、期数n，求解年金A。

解：

A＝P／（P／A，12％，10）＝1000／5.6502≈177（万元）

如例2－9，已知年金现值P、年利率i和期数n，求解年金A的问题称为年资本回收额的计算。年资本回收额是指在约定年限内等额回收初始投入资本或清偿所欠债务的金额。年资本回收额与普通年金现值互为逆运算，其计算公式为：

事实上，有些实际问题由于利率不是整数而无法通过查系数表的方法进行简便计算。例如，你准备抵押贷款400000元购买一套房子，贷款期限20年，每月偿还一次；如果贷款的年利率为8％，每月贷款偿还额为多少呢？其中，贷款的月利率为0.67％ （8％／12），期数n＝240，则抵押贷款的月支付额为：[

0.0067 400 000×

1－（1＋0.006 7）

－240]＝3355.72（元）

2.预付年金

预付年金是指从第一期起，每期期初发生等额现金流量的现金流系列。由于预付年金是在期初发生现金流入或流出，故又称先付年金、即付年金。图2－7为n期预付年金。

图2－7 n期预付年金示意图

1）预付年金终值的计算

每期期初现金流量A的复利终值之和，即为预付年金的终值，计算公式为：

F＝A（1＋i）1＋…＋A（1＋i）n－3＋A（1＋i）n－2＋A（1＋i）n－1＋A（1＋i）n

上式中各项为等比数列，整理可得两个计算公式：

或：

公式 （2－9）中的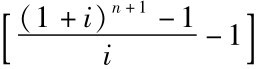n＋1是预付年金终值系数，同普通年金终值系数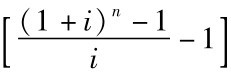相比，期数加1，而系数减1，可记作 ［（F／A，i，n＋1）－1］，并可利用“年金终值系数表”查得 （n＋1）期的系数值，减去1后，得出预付年金的终值系数。也可以采用公式 （2－8），直接利用n期普通年金终值计算公式乘以 （1＋i），即可计算n期预付年金的终值。

2）预付年金现值的计算

每期期初现金流量A的复利现值之和，即为预付年金的现值，计算公式为：

P＝A＋A（1＋i）－1＋A（1＋i）－2＋A（1＋i）－3＋…＋A（1＋i）－（n－1）

对上式稍作推导，可得下面两个计算公式：

或：

公式 （2－11）中的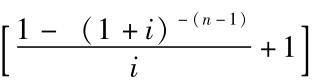是预付年金现值系数，同普通年金现值系数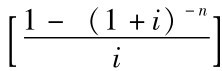相比，期数减1，而系数加1，可记作 ［（P／A，i，n－1）＋1］，并可利用“年金现值系数表”查得 （n－1）期的系数值，加上1后，得出预付年金的现值系数。也可采用公式 （2－10），直接利用n期普通年金现值计算公式乘以 （1＋i），即可计算n期预付年金的现值。

【例2－10】 政府对有突出贡献的青年科学家发放年金式的政府津贴，每年人民币10000元，从年初开始，共发放10年。假设10年期的银行存款利率为8％，这笔津贴的现值是多少？

分析：

本题中预付年金A＝10000万元，n＝10年，i＝8％

解：

P＝A（P／A，8％，10）（1＋8％）＝10000×6.7101×（1＋8％）＝72469（元）

或：

P＝A［（P／A，8％，10－1）＋1］＝10000×（6.2469＋1）＝72469（元）

【例2－11】 周教授是中科院院士，一日接到一家上市公司的邀请函，邀请他作为公司的技术顾问，指导开发新产品。邀请函的具体条件如下：

（1）每个月来公司指导工作1天；

（2）每年聘金10万元；

（3）提供公司所在A市住房1套，价值80万元；

（4）在公司至少工作5年。

周教授对以上工作待遇很感兴趣，对公司开发的新产品也很有研究，决定应聘。但他不想接受住房，因为每月工作1天，只需要住公司招待所就可以了，这样住房不用专人照顾，因此，他向公司提出，能否将住房改为住房补贴。公司研究了周教授的请求，决定可以每年年初给周教授补贴20万元房贴。

收到公司的通知后，周教授又犹豫起来。如果向公司要住房，可以将其出售，扣除售价5％的契税和手续费，他可以获得76万元，而若接受房贴，则每年年初可获得20万元。假设每年存款利率2％，则周教授应如何选择呢？

分析：

要解决上述问题，主要是要比较周教授每年年初收到20万元房贴的现值与售房76万元的大小问题。

解：由于房贴每年年初发放，因此对周教授来说是一个预付年金。其现值计算如下：

P＝20×［（P／A，2％，5－1）＋1］＝20×（3.8077＋1）＝20×4.8077＝96.154（万元）

从这一点来说，周教授应该接受房贴。

如果周教授本身是一个企业的业主，其企业的投资回报率为32％，则周教授应如何选择呢？

在投资回报率为32％的条件下，每年20万元的住房补贴现值为：

P＝20×［（P／A，32％，5－1）＋1］＝20×（2.0957＋1）＝20×3.0957＝61.914（万元）

在这种情况下，周教授应接受住房。

【例2－12】 某企业有一个投资项目，预计在2001—2003年每年年初投入资金300万元，从2004—2013年的10年中，每年年末流入资金100万元。如果企业的折现率为8％，试判断该投资项目是否可行。

分析：

首先画出现金流时间线。根据图2－8可知，该投资项目的前3年为投入期资金流出，后10年为产出期资金流入，只有产出大于投入，该项目才可行。将产出和投入的金额换算到同一时点，才能进行比较，第3年年末是作比较最简便的时点。

图2－8 投资项目的现金流时间线

解：

（1）将前3年的资金流出看作3期的预付年金，计算其第3年年末的终值：

F＝300×（F／A，8％，3）×（1＋8％）＝300×3.2464×1.08＝1051.83（万元）

（2）将后10年的资金流入看作10期的普通年金，计算其第3年年末的现值：

P＝100×（P／A，8％，10）＝100×6.7101＝671.01（万元）

（3）671.01＜1051.83，由于该项目的现金流出大于现金流入，所以项目不可行。

3.递延年金

普通年金和预付年金是年金的基本形式，都是从第一期开始发生等额现金流量，而递延年金是派生出来的年金，是指从第二期或第二期以后才发生等额现金流量的年金。图2－9为递延期2期的递延年金。

图2－9 递延年金示意图

递延年金终值的大小与递延期无关，只与年金共支付了多少期有关，它的计算方法与普通年金相同。直接利用普通年金终值的计算公式F＝A×（F／A，i，n）进行计算，在此式中，n表示A的个数。

递延年金现值的计算有多种方法，下面结合例题说明。

【例2－13】 某项年金前3年无现金流入，后5年每年年初流入500万元，若年利率为10％，其现值为多少？

分析：

首先正确画出现金流时间线，如图2－10所示，并据此判断年金类型为递延年金。在图2－10中，后5年指的是第4年到第8年，第4年年初即第3年年末，从第3年年末开始发生现金流量，所以递延期为m＝2年。

图2－10 该项年金的现金流时间线

方法1：先假设递延期也发生现金流入，则递延年金演变成7期普通年金，求出7期普通年金现值，再扣除递延期2期的普通年金现值。

P＝500×（P／A，10％，7）－500×（P／A，10％，2）＝1566.45（万元）

方法2：先求出5期普通年金的现值，该现值应在递延期末，即第2年年末，然后再将此现值调整到第1期期初，该方法共经过两次折现。

P＝500×（P／A，10％，5）×（P／F，10％，2）＝1566.36（万元）

方法3：先求出5期普通年金在第7年年末的终值，再将该终值折算为现值。

P＝500×（F／A，10％，5）×（P／F，10％，7）＝1566.57（万元）

三种方法所得结果的差异是由于系数四舍五入造成的。

请思考还有什么方法可以计算该项年金的现值。

【例2－14】 根据例2－12的资料和图2－8，试通过比较该项目投入和产出的现值，来判断该投资项目是否可行。

解：

（1）计算3期预付年金的现值：

P＝A［（P／A，8％，3－1）＋1］＝300×（1.7833＋1）＝834.99（万元）

（2）利用两次折现的方法，计算递延年金的现值：

P＝100×（P／A，8％，10）×（P／F，8％，3）＝100×6.7101×0.7938＝532.65（万元）

（3）532.65＜834.99，由于该项目的现金流出大于现金流入，所以该项目不可行。

4.永续年金

永续年金可以看成n趋向无穷大的普通年金，是普通年金的一种特殊形式。永续年金没有终止的时间，即没有终值。永续年金的现值可以通过普通年金现值的计算公式导出。

普通年金现值计算公式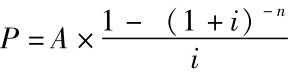，当公式中n趋向于无穷大时，由于A、i都是有界量，（1＋i）－n趋近于0，因此永续年金现值P趋向A／i。永续年金现值计算公式为：

P＝A／i（2－12）

由公式 （2－12）可知，当利率变化时，永续年金现值将变化很大。

【例2－15】 大通公司拟建立一项永久性的基金资助西南干旱地区，年计划资助50万元。若利率为8％，现在应存多少钱？

解：

P＝A／i＝50／8％＝625（万元）

假如例2－15中，每年资助的金额不是固定不变的，而是以每年3％的速度在增长，如果这种增长趋势会永远延续下去，这种现金流量序列就称为永续增长年金。假如增长率用常数g来表示，可以得出此类问题的计算公式：

P＝A（1＋i）－1＋A（1＋g）（1＋i）－2＋A（1＋g）2（1＋i）－3＋…＋A×（1＋g）（n－1）（1＋i）－n

该公式可简化为：

公式 （2－13）中，A为第1期期末的现金流量，而不是现在 （第0期）的现金流量；只有当折现率i大于增值率g的情况下，该公式才有意义。

回到例2－15中，如果大通公司每年资助的金额以3％的速度增长，则这笔永续增长年金的现值为：