贴现率和期数的计算

在资金时间价值的计算公式中含有四个要素，只要知道其中三个，就可以推导出第四个。在单笔现金流量终值和现值的计算中，已知P、F和n，可以推导出利率i，或已知P、F和i，可以推导出期数n。同样，在年金终值和现值的计算中，已知P（F）、A和n，可以推导利率i，或已知P（F）、A和i，可以推导出期数n。

【例2－16】 王先生现在有现金30000元，准备5年之后买一辆车，估计届时该车价格为48315元。假如将现金存入银行，那么在年复利率为多少时，王先生才能在5年后美梦成真呢？

分析：

本例已知P、F、n，求解i。

解：

F＝P（F／P，i，5）

48315＝30000×（F／P，i，5）

（F／P，i，5）＝48315÷30000＝1.6105

查复利终值系数表，在n＝5一行上找到复利终值系数1.6105，该系数对应的利率为10％。因此，当利率为10％时，才能使王先生5年后美梦成真。

在例2－16中，如果某一已知条件发生变化，如5年后车的价格不是48315元，而是48000元，那么例2－16中的系数 （F／P，i，5）则等于1.6，将无法在复利终值系数表中n＝5一行上直接查到，在这种情况下，应该采用内插法估算利率。内插法可以用来估计利率和期限，实际上就是比例法。求利率时，利率差之比等于系数差之比；求期数时，期数差之比等于系数差之比。利用内插法估算利率的计算公式为：

公式（2－14）中，所求利率为i，i对应的现值（或者终值）系数为B，B1、B2为现值（或者终值）系数表中与B相邻的两个系数；i1、i2为B1、B2对应的利率。如果利用内插法估算期数n，即把公式 （2－14）中的i换成n即可：

【例2－17】 老张年初借款20000元，每年年末还本付息额为4000元，连续9年付清。计算借款利率是多少？

分析：

本例是已知年金现值P、年金A和期数n，计算利率i。

解：

P＝A（P／A，i，9）

20000＝4000×（P／A，i，9）

（P／A，i，9）＝5

查年金现值系数表，在n＝9一行上无法查到刚好等于5的系数，因此需要采用内插法对利率进行估算。在n＝9一行上找到大于和小于系数5的临界系数值，分别为B1＝5.3282＞5， B2＝4.9164＜5，同时查出两个临界系数对应的利率i1＝12％，i2＝14％。代入公式（2－14）得：

老张的借款利率为13.59％。

【例2－18】 某企业计划购买新设备一台，可供选择的设备有甲、乙两种类型。甲设备比乙设备价格贵8000元，但每年的使用费低2000元，问：若该企业折现率为10％，甲设备使用寿命为多少年时，才应购买甲设备？

分析：

本例是已知年金现值P＝8000元、年金A＝2000元和利率i＝10％，计算期数n。

解：

P＝A（P／A，10％，n）

8000＝2000×（P／A，10％，n）

（P／A，10％，n）＝4

查年金现值系数表，在i＝10％一列上无法查到刚好等于4的系数，因此需要采用内插法对期限进行估算。在i＝10％一列上找到大于和小于系数4的临界系数值，分别为B1＝4.3553＞4，B2＝3.7908＜4，同时查出两个临界系数对应的期数n1＝6，n2＝5。代入公式（2－15）得：

甲设备至少使用5.4年才应购买。

此外，在复利终值和现值的计算中，利率i也可以直接通过公式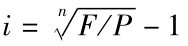计算得到。根据例2－16的资料，将数据代入公式可解出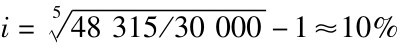。在永续年金现值的计算中，利率可以通过公式i＝A／P进行计算。