分析计算法又称定量预测法。分析计算法可分为两种：一种是时间序列分析法，或称历史延伸法，大多用于中期、短期预测；另一种是回归分析预测法，又称因果预测法，多用于中期、长期预测。
一、时间序列分析法
所谓时间序列，是观察或记录一组按时间顺序排列起来的数字序列。时间序列分析法用于预测的基本原理，是认为事物的发展具有连贯性和相似性，过去的发展趋势会延续到未来。时间序列分析法从本质上讲，是一种趋势外延法。它利用过去到现在为止的历史资料进行预测，其预测的可靠性与外推时间的长短有关，一般外推时间不长于原始动态序列的1／3。它适用于市场变化比较稳定的预测对象，作中期、短期预测的效果较好。
（1）移动平均法
移动平均法是时间序列分析法中较简单的一种，是在简单算术平均法的基础上发展起来的。移动平均法采用分段平均，并按数据点的顺序，逐点移动，求得下一个时间的预测值，用靠近预测期的各期实际销售额的平均数来预测未来时期的销售额。其基本公式如下：
式中：M t——t＋1期的预测值；
Xt——t期的实际值（t＝1，2…，t）；
N——移动资料期数。
在（5‐1）式中要注意，当N＝1时，Mt＝Xt，相当于数据点的自然分布；当N等于数据点的总个数时，Mt等于所有数据点的算术平均数。
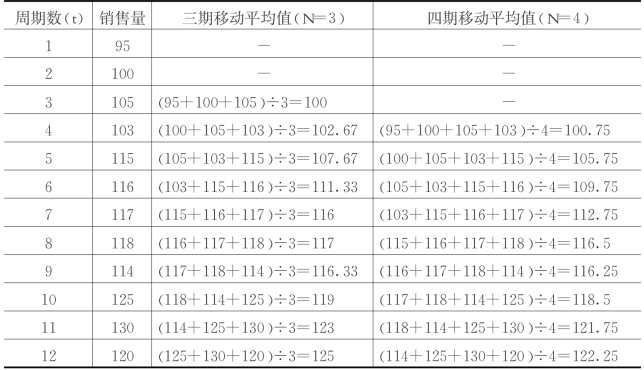
例如：某企业厂1—12月份的实际销售量和预测值，如表5．2所示。从表中可以发现，预测值同移动平均所用的移动期的长短有关。N＝4时的移动平均值比N＝3时的移动平均值的反应速度要慢，这是由于对参加移动的数据一律等同对待所致。在市场预测中，最新的数据更能反映销售趋势。为此，也可采用加权移动平均进行预测，其数学模型如下：
表5．2 移动平均法举例
且
式中：WM t——下一期预测值；
Xt——各期实际值；
Ct——各期权数。
在用（5‐1）式进行预测时，如果N增大，计算量也会加大。为计算简便，可采用递推算法，将（5‐1）式变为（5‐3）式。
根据上例资料，用（5‐3）式同样可以求出N＝3时，6月份的预测值：
采用移动平均法进行预测，一般可以消除在移动期内销售量的波动，能在一定程度上反映销售量变化的趋势，其反应灵敏的程度取决于N值的大小。N值过大，预测趋势的灵敏度较差，此时虽能消除季节性因素的影响，但“滞后现象”显著增加。N值过小，预测趋势的灵敏度较好，但由于波动过多，难于反映趋势变化。为此，一定要根据预测问题的特点，选择合适的N值。
（2）指数平滑法
移动平均法的优点是考虑新的数据比较容易，但它将每一个数据同等看待，并且需要储存较多的历史数据。实际上，远期的变化趋势和近期的变化趋势对预测未来的影响是不同的，一些新产品和时令性较强的产品往往也难于收集到较多的数据。而指数平滑法既具有移动平均法计算简便的优点，又能考虑到不同时期数据作用的大小。它只需要具备本期实际数、本期预测数和平滑系数三种资料就可以进行预测，从而大大减少数据存储量。
指数平滑法的基本公式如下：
或 St＝St－1＋α（Xt－1－St－1）（5‐5）
式中：St——第t期预测值；
Xt－1——第t－1期实际值；
St－1——第t－1期预测值；
α——平滑系数（0≤α≤1）。
式中：平滑系数α值的大小，可以按其在不同时期的因素在预测中所起作用的大小而定。α值越大，近期因素所起的作用越大，否则相反。当α＝1时，St＝Xt－1，即t期的预测值等于t－1期的实际值；当α＝0时，t期的预测值等于上期的预测值。
为了进一步了解指数平滑法的含义，现将指数平滑法的公式作如下推演：
用②式和③式代入①式：
以此类推，可得出：
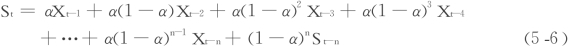
从上式可以看出，指数平滑法预测，实际上包含了所有的原始数据。只是随着时间的推移，离现时刻越远的数据加权越小，权系数分别为α，α（1－α），α（1－α）2，…由于权系数是指数的几何级数，指数平滑法也由此而得名。指数平滑法的具体应用，举例如下。
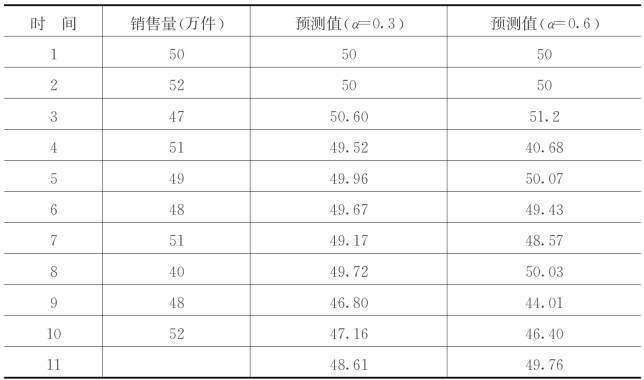
例如：某企业某种产品1—10月份的实际销售量和预测值，如表5．3所示。如果α＝0.3，则2月份和11月份的预测值分别为：
表5．3 指数平滑法举例
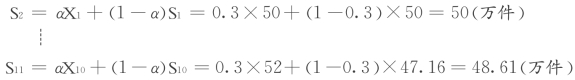
（3）季节性系数法
某些产品的市场需要量要受季节性变化的影响，呈现一种有规律的季节性波动，表现出很强的时令性。要想准确地预测这些产品的市场需要量，必须预测季节性因素影响的程度。季节性系数法预测，是对已有的历史资料进行季节性平滑，求出季节性系数，然后利用季节性系数对预测值进行修正。经过修正后的预测值，一般能较准确地反映产品的市场需要量。
例如：某饮料公司从1998—2001年各季度的销售量如表5．4所示，试预测2002年第一、二季度市场需要量。
表5．4 季节性系数法举例
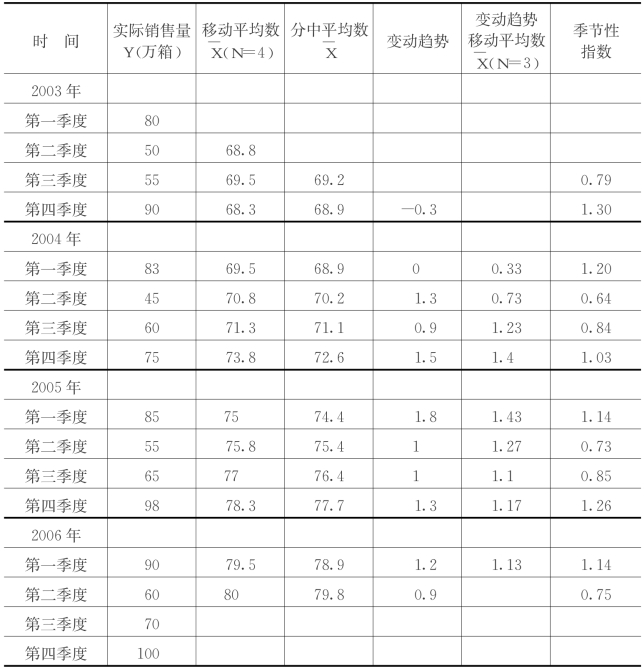
表5．4中的资料表明，该产品的市场需要量有明显的季节性波动，可用季节性系数法来进行预测。其步骤如下：
第一步，求消除季节性影响的历年分季平均数。
①计算实际销售量的移动平均数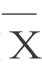
（N＝4）＝68.8＝（80＋50＋55＋90）÷4；
②计算分中平均数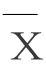
，如表5．4中第五行的69.2＝（68.8＋69.5）÷2，其余类推。
③计算变动趋势值，即下一个分中平均数与上一个分中平均数差的绝对值，如表5．4中变动趋势栏第六行的－0.3＝（69.2－68.9）。
④计算消除季节性影响的历年分季平均数，即计算变动趋势移动平均数X（N＝3）＝0.33＝（－0.3＋0＋1.3）。
第二步，求每年每季的季节性指数。
每年每季的季节性指数是分中平均数与实际销售量的比值。例如，2005年第四季度的季节性指数为：
98÷77.7＝1.26
第三步，计算季节性系数（表5．5）。
表5．5 计算季节性系数
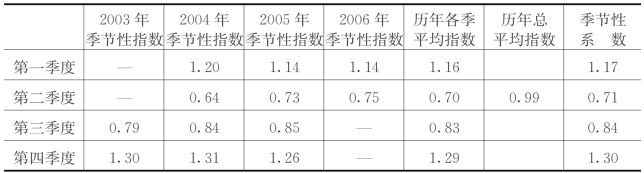
①计算历年各季节性指数的平均数。
历年第一季度的平均指数为：（1.2＋1.14＋1.14）÷3＝1.16
历年第二季度的平均指数为：（0.64＋0.73＋0.75）÷3＝0.70
历年第三季度的平均指数为：（0.79＋0.84＋0.85）÷3＝0.83
历年第四季度的平均指数为：（1.3＋1.31＋1.26）÷3＝1.29
②计算历年总平均指数，即历年各季度平均指数的平均数。根据上述数值，可求得结果为：
（1.16＋0.70＋0.83＋1.29）÷4＝0.99
③计算季节性系数，即用历年各季的平均指数除以总平均指数。
第一季度季节性系数为：1.16÷0.99＝1.17
第二季度季节性系数为：0.70÷0.99＝0．71
第三季度季节性系数为：0.83÷0.99＝0.84
第四季度季节性系数为：1.29÷0.99＝1.30
季节性系数等于1，表明市场需要量不受季节性影响；季节性系数大于或小于1，表明市场需要量受季节性影响；季节性系数愈是大于或小于1，说明受季节性影响的程度愈大。
第四步，进行市场需要量预测。
①预测消除季节性影响的市场需要量。其计算公式为：
y＝Xa＋（X）b・t
式中：y——市场需要量预测值；
Xa——移动平均数中的末项值；
（X）b——变动趋势移动平均数中的末项值；
t——间隔期（末项移动平均数距离预测期的间隔）。
例如：2007年第一季度的市场需要量是：80＋1.13×3＝83.39（万箱）
2007年第二季度的市场需要量是：80＋1.13×4＝84.52（万箱）
②预测考虑季节性影响的市场需要量。其计算方法是将消除季节性影响的预测值乘以该季的季节性系数。例如：
2007年第一季度的市场需要量是：83.39×1.17＝97.56（万箱）
2007年第二季度的市场需要量是：84.52×0.71＝60（万箱）
二、回归分析预测法
回归分析预测法，是通过处理大量的统计数据，从中寻求这些数据演变规律的一种数理统计预测方法。其过程是：首先对所收集的数据进行统计分析，导出自变量与因变量之间的关系式，即回归方程式；然后求解方程式中的未知系数，并根据自变量的取值来预测因变量的取值范围；最后对取值范围及可信区间进行估计。
回归分析预测法的基本公式是：
y＝f（x1、x2、…、xn）
式中：y——因变量；
x1、x2、…、xn——n个自变量。
根据数学模型中自变量的多少，自变量和因变量的关系，回归分析预测法可分为一元线性回归法，多元线性回归法及非线性回归法等等。
回归分析预测法，是在定量分析的基础上进行预测的，要得到理想的预测效果，预测对象应满足下列几个条件。
①预测对象与影响因素之间必须存在因果关系，而数据点以在20个以上为好。
②过去和目前的数据规律，能够反映未来。
③数据的分布确有线性或非线性趋势。
（1）一元线性回归法
一元线性回归法是处理两个变量间的因果关系的一种用途很广的方法。其基本数学模型如下：
式中：y——因变量，即预测值；
x——自变量；
a、b——回归系数。
确定回归系数a和b，一般可根据最小二乘法的原理求得以下方程组：
解方程得
式中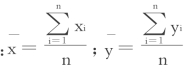
；n为资料期数。
回归分析预测法的因变量可以是时间，也可以是其他相关因素。回归分析预测法既可以用于时间序列分析，又可以用于因果（相关）分析。下面分别介绍回归分析预测法的这两种不同用途。
①用于时间序列分析。如果（5‐7）式中的自变量x代表取得统计数据的时间，则预测就属于时间序列分析。从（5‐8）式可见，∑xi是一个共同的因子。为了简化计算，可以设法使∑xi＝0。若n为奇数，则取t的时间间隔期为1，将t＝0置于资料的中央一期，其上为负值，其下为正值。若n为偶数，则取t的时间间隔期为2，将t＝－1与t＝1置于资料中央的上下两期，其上为负值，其下为正值。
当∑xi＝0时，方程组（5‐8）就成为：
解方程组可得：
例如：已知某企业1995—2001年的逐年销售额如表5．6：
表5．6 某企业逐年销售表
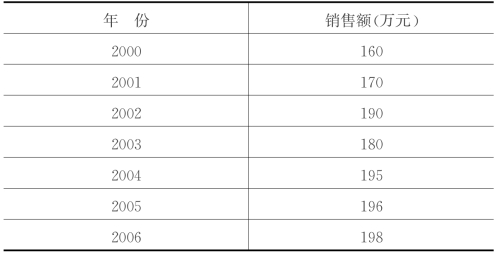
试运用这些数据，预测2007年和2008年的销售额。
根据回归分析预测法的要求，将数据加以整理分析，如表5．7所示。将表中数字代入（5‐12）式和（5‐13）式中，即可算出a、b值。
表5．7 一元线性回归法用于时间序列分析举例
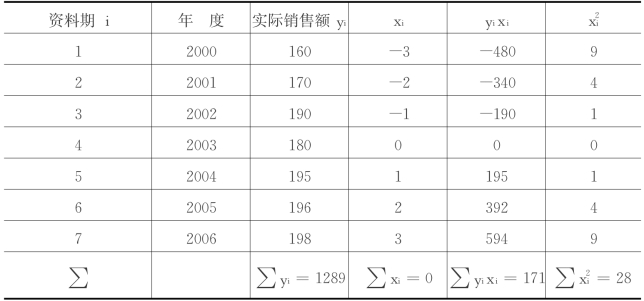
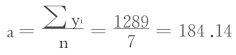
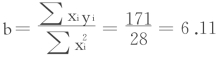
将a、b值代入（5‐7）式，就可求得2007年销售额的预测值为：
y＝a＋bx＝184.14＋6.11×4＝208.58（万元）
同理，可求得2008年销售额的预测值为：
y＝a＋bx＝184.14＋6.11×5＝214.69（万元）
②用于因果（相关）分析。产品的销售量不仅与时间有关，还与许多社会、技术、经济、心理因素有关。例如，纺织品的销售量与人口的多少，与人们可支配的销售收入的多少，与新产品的开发，都有明显的因果关系。这里，可以让自变量x代表某种社会、技术、经济、心理因素，因变量的变化取决于x的变化，因变量y就是所需要的预测值。
例如：某地区2000—2006年间，商品零售总额与人们用于穿着商品零售额的资料，如表5．7。令用于穿着商品零售额为因变量yi，商品零售总额为自变量xi；按表5．8所提供的资料，可以直观地判断人们衣着商品零售额与商品零售总额的相关关系，从而可以利用y＝a＋bx的直线回归方程进行预测。根据公式（5‐9）、（5‐10），可以求出回归系数a、b值。
表5．8 一元线性回归法用于因果（相关）分析举例
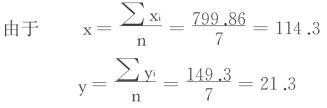
代入（5‐9）、（5‐10）式，可求得回归系数a、b值如下：
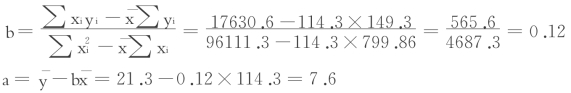
故 y＝a＋bx＝7.6＋0.12 x
即当商品零售总额每增加一亿元时，其中用于衣着零售额则增加0.12亿元。
表5．8中2006年的穿着零售额预测值：Y＝7.6＋0.12×152＝25.8
用回归分析预测法进行预测时，预测值和实际值之间总会有差异。为了确定预测值的置信程度及其可能的波动范围，应该估计预测值的置信区间。为了估计置信区间，必须计算标准偏差σ，σ是确定置信区间的参数。
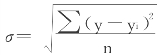
式中：yi——某期实际值；
y——某期预测值；
n——资料期数。
假如利用表5．7中的数据计算，则
如果该地区2007年商品零售总额为165亿元时，则预测用于衣着零售额为：
yi＝a＋bx＝7.6＋0.12×165
＝27.45（亿元）
如果要求预测值的置信程度为95%，落在正态分布中心值±2σ范围内，则2007年用于衣着零售额的置信区间应是：
27．45±2×0.59＝28.58～26.22（亿元）
也就是说，2007年用于衣着零售额估计为26.22亿～28.58亿元。
二、多元线性回归法
影响产品销售额的因素往往很多，有时要利用多元线性回归法来进行预测。多元线性回归法是根据两个或两个以上的自变量，来估计因变量。其基本数学模型是：
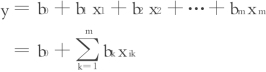
式中：y——因变量；
xik——自变量；
bk——回归系数。
多元线性回归法求系数的原理同一元线性回归法一样，也是用最小二乘法，使预测值与实际值之间的平方差之和最小，求出多元回归系数，实现回归方程与实际数据点的最佳拟合。
在多元线性回归法中，最常用的是二元线性回归法，它可以同时研究两个自变量对因变量影响的程度，其基本数学模型是：
式中：y——预测值（因变量）；
x1，x2——影响因素（自变量）；
a，b1，b2——回归系数。
根据最小二乘法和求极值的原理，可得以下方程组：
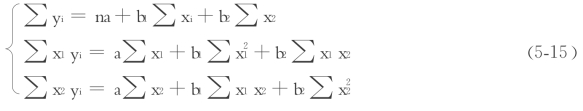
多元线性回归法的计算，用手工计算是很难完成的，一般必须利用矩阵方法和计算机运算。具体的计算过程就不一一列出了。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
