【摘要】:对具有三道相同工序的生产排序问题,如果符合下列两个条件中的任何一个,则也可用约翰逊-贝尔曼法则,将三台机床合并为两台加以求解。 5种零件在3台机床上的加工时间(小时)见表9.7所示。
对具有三道相同工序的生产排序问题,如果符合下列两个条件中的任何一个,则也可用约翰逊-贝尔曼法则,将三台机床合并为两台加以求解。两个条件是:
①min tAi≥max tBi
②min tCi≥max tBi
注:tAi、tBi、tci分别为三台机床的加工时间。
具体方法是:将第1、2道工序的加工时间相加,作为假想设备G的加工时间;将第2、3两道工序的加工时间相加,作为假想设备H的加工时间。再应用约翰逊-贝尔曼法则来安排加工顺序。
【例9‐2】 5种零件在3台机床上的加工时间(小时)见表9.7所示。
表9.7 5种零件的加工时间表单位:小时
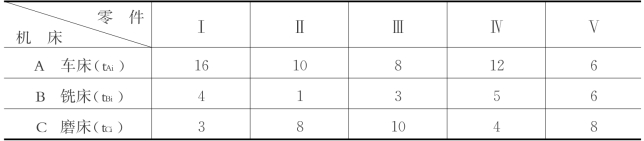
因为,m in tAi(=6)=max tBi(=6),符合条件(1),故可将3台机床变换为两台假想机床,并求出五种零件在两台假想机床上的加工时间,如表9.8所示。
表9.8 假设的加工时间单位:小时

依照约翰逊-贝尔曼法则,求出本例题加工顺序的最优解为:
Ⅲ-Ⅴ-Ⅳ-Ⅱ-Ⅰ
加工时间示意图见图9.11。5种零件的总加工周期为:
8+6+12+10+16+4+3=59(小时)

图9.11 用约翰逊法处理后的加工时间示意图
本例中,第Ⅱ个零件与第Ⅳ个零件的t Hi都是9,由此也可得出第二种排序:
Ⅲ—Ⅴ-Ⅱ-Ⅳ-I
其总加工周期也是59(小时),与第一种排序相同。
对于四种以上设备也可以按此法处理,得出的结果近似最优解。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。













