汽车召回决策已知条件

缺陷汽车的产品召回是一个随机决策问题， 政府对汽车召回的决策选择主要体现在如何进行决策选择能使政府的边际效益最大化。 而根据第7章政府和制造商的博弈来看， 政府的效益主要体现在： 发现更多的缺陷， 控制更多的事故， 降低更多的伤亡和损失。 对于政府的决策行为， 可以先分析不同条件时的决策行为， 求取此条件下的边际效益， 进而综合多属性来求解同时满足两条件下的政府行为决策。

10.2.1 已知汽车召回发生概率的策略选择

汽车制造商和所制造出的汽车品牌车型数量是庞大的， 以美国市场上出现的汽车品牌为例， 美国市场在售的汽车品牌有2000多种， 还不包括不同车型的汽车。 按照以往的统计数据来看， 几乎每一种汽车在美国都发生过召回。 为了使政府的资源效益最大化， 在资源——财政拨款b和人员d的限制下， 面对市场上所有可能出现的汽车缺陷， 如何分配人员和资金， 才能使政府所产生的效益最大——尽可能地消除缺陷， 减小交通事故带来的人民生命和财产的损失， 最大限度地保证社会公共安全。

假设市场上出现很多汽车缺陷，汽车缺陷的召回概率为pri，缺陷会造成事故损失为ki。首先要进行检测，确认哪些车辆存在缺陷，哪些不存在缺陷。检测某一个汽车缺陷需花费检测资金ci和配备人员ri。则求政府在有限资源——财政拨款b和人员d的条件下获得的最大效益。

政府资源的最大效益为： 消除了汽车缺陷所带来的效益－政府付出的成本， 即用公式表示为

下面建立政府资源的最大效益的数学模型。

目标是使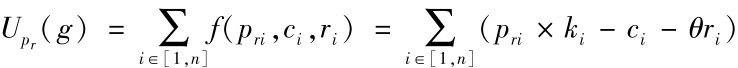最大， 条件是具有财政拨款为b和人员为d， 即需满足

式中，ci表示分配给第i个汽车缺陷的检测资金；ri表示分配给第i个汽车缺陷的人员；pri为第i个的召回概率pr；f（pri，ci，ri）表示为第i个汽车缺陷的政府有限资源的效益。

检测资金ci和人员ri与概率无关，即付出的成本和召回概率没有直接的联系， 但是每次召回的收益却是召回概率的函数。 因此， 汽车的召回概率越大， 潜在的交通事故的严重性或已经发生事故的严重性很大，如果不进行召回， 所带来的交通事故的数量或者严重程度， 以及造成的损失必将很大； 如果进行召回， 则所消除的交通事故的风险就大， 意味着交通事故的发生率和事故的严重性也大。 根据Bae的研究结果， 召回将降低交通事故的发生数量和事故的严重程度。 这些都是政府资源为维护公共安全所得到的效益。因此，可以推出，当汽车的召回概率pr越大时， 所消除的汽车缺陷的事故风险值越大， 政府有限资源效益也越大。因此，政府有限资源效益f（pri，ci，ri）为召回概率pr的正相关函数。

结论1：汽车召回的概率pr越大，每次召回的平均检测成本越小，平均效益越大， 政府有限资源的总效益也越大。

根据这个结论， 要使政府有限资源的效益最大化， 则政府应该着力于召回概率最大的那些缺陷汽车。

结论2： 政府所关注的缺陷汽车数目取决于政府的财政拨款和人员配备。

政府可能需要进行检测的汽车品牌有很多， 每次检测都要付出检测费用ci和配备一定的人员ri，政府的总财政拨款为b，人员总编制为d。

假设每次检测费用一样为c， 每次所需的人员也一样为r， 则可以得到

政府所能使用的资源取决于M和N中的较小值， 即min｛M，N｝。

根据推论，f（pri，ci，ri）是pr的函数，pr越大，f（pri，ci，ri）也越大。

政府有限资源的效益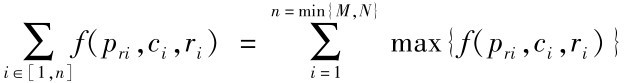为pr的函数。可见pr越大，政府有限资源的效益也越大。即

因此， 在已知召回概率的条件下， 政府有限资源的效益最大化的原则为：将所有缺陷汽车的召回概率pr进行从大到小的顺序排列，选择前N个召回概率的那些缺陷汽车。

10.2.2 已知汽车制造商的召回主动度的策略选择

根据第7章的分析可知， 在汽车召回的博弈中， 政府和汽车制造商是不完全信息的动态博弈。当市场信息失灵时，政府进行干预［68，151，152］。政府资源的有限性决定了政府只能在汽车制造商选择了召回行动之后，再进行召回的策略选择。 政府在了解了汽车制造商的行动意向后， 根据汽车制造商的行动意向做出相应的反应： 政府的决策行为应该和汽车制造商的决策行为互为相反数， 即汽车制造商的召回主动度大， 政府的投入资源应该相对较小； 而当汽车制造商的召回主动度小时， 政府的投入资源应该相对较大。 政府策略选择的问题其实也就是政府有限资源的最优化配置的过程。 因此， 可以用最优化的理论来进行分析。

从缺陷汽车召回博弈树 （图7.1） 中可以看出， 博弈分两阶段进行： 第一阶段T＝1， 汽车制造商1对汽车召回进行博弈， 第二阶段T＝2， 政府2对汽车召回行为进行博弈。 政府2因为财政投入有限， 在召回决策选择时， 会依照制造商1的行为结果来决定召回行为。 当制造商1发起召回时， 政府2的最优策略是不发起召回； 而当制造商1不发起召回时， 政府2的最优策略是发起召回。 制造商1主动发起召回的概率为t。

博弈过程通过反向归纳法来分析。 T＝2时， 政府2观测到制造商1的行动为召回， 选择策略 （召回， 不召回）， 政府资源效益最大化的期望为

当且仅当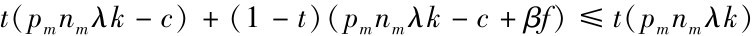，即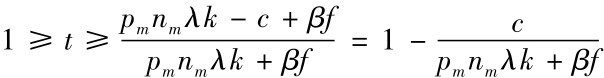时，政府2选择不召回。

T＝1时， 制造商1了解自己的类型， 并预期到政府的行为为 （召回， 不召回）， 因此制造商也进行 （召回， 不召回） 的策略选择， 最大化自己的支付函数。

②当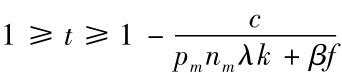时，制造商1预期到政府不召回，制造商1的最优化反应行为是max｛－pmnmrm－xmk－c，－pmnmλk｝，从而制造商1选择召回的充要条件是c＋pmnmrm＋xmk＜pmnmλk，即要使制造商1召回的充要条件是： 汽车召回所发生的成本 （检查费用、 缺陷部件的更换成本和对已经发生事故的赔偿费用之和） 小于汽车缺陷所引起的事故的赔偿成本。