第7章 投资组合分析的基本方法
投资新闻7
FT
基金经理人对无固定利息证券投资态度谨慎
一项调查发现,世界范围内的基金经理人都因为对伊战争可能带来的不确定情况而采取了“极端”的风险规避措施。Merrill Lynch公司表示,一项对基金经理人的月度调查显示,当前基金经理人的风险规避程度比“9·11”恐怖袭击之后还要高。这样一来,一些风险更低的投资项目,比如说现钞交易和长期国库券,就成了人们投资的热点,这些投资项目吸引的资金量也已有了很大的攀升;而与此相对照的却是那些无固定利息的证券,这些证券吸引的投资金额持续下滑,屡创新低,已是4年来的第三次了。
接受该公司调查的308位基金经理人中过半的人都认为,无固定利息的证券已经在全球范围内遭遇价值缩水,而持有这种看法的人总共控制了约7140亿美元的资金。自投资银行于2001年在全世界范围内开展此项调查以来,持有这种看法的经理人所占的比例是历届最高的。其中1/4的被调查者认为股票的市场价值缩水了15%以上。
马克·哈特奈特(Mark Hartnett)是该公司负责欧洲市场的首席策划,他说,宏观经济上的顾虑是会造成一些不确定的情况,但地缘政治的危机更能让大众绷紧神经。“最重要的因素是伊拉克。”哈特奈特先生说,如果现金持有量在过去已经增加了的话,投资者中的悲观主义情绪也许会跟着复苏。尽管如此,这个复苏能否维持到这场地缘政治危机得以解决的那一天还很难说。“当你作为一个投资人,在某一天看到报纸头条报道说,北约也许就要解散了,你一定也会想,这可是一个重要的地缘政治危机,应该把它的影响纳入投资的考虑范围之内。”
Merrill Lynch公司的调查还表明,有被调查者说,他们现在正在运用比正常情况稍低的风险规避策略来决定向什么项目投资。持有这种观点的受访者在1月份占所有受访者的25%,而在2月份已经上升到了34%。整整25%的受访基金经理表示,他们的现金持有量已经超过正常的持有量了。而在一个月以前,只有12.5%的受访基金经理做出这样的表示。每项资产投资组合中的平均现金持有量在2月份是4.9%;与此相对照的是,在1月份平均现金持有量还占到了4.2%。每6个基金中就有1个现金持有量超过12%。在所有受访基金中有11%的基金证券持有量不足,而这个数据也大大低于1月份的30%。与此同时,报告还说,证券持有量不足的资产配置者远多于股票持有量过多的投资者,这在4年中也是第三次出现。
投资者对无固定利息证券采取的审慎态度与他们对收入与经济增长的乐观形成了鲜明对比。62%的受访者预期,未来一年的世界经济将有一个较强的增长势头,七国集团成员国平均国民生产总值将有3%的增长。明年全年全球平均单股收益也预计会有7%的增幅。71%的受访者认为带动收益增加的主要因素是成本有所下降。戴维·鲍尔(David Bowers)是该公司的首席投资策略顾问,他说:“如果风险规避可以由于某种原因而得以解除,当前的一些条件就可以促成全球证券市场出现一个策略性的反弹。”
资料来源:托尼·泰斯尔:《基金经理人对无固定利息证券投资态度谨慎》,《金融时报》2003年2月19日。
学习目标
在完成本章的学习后,你应能够:
1.解释一些基本概念,比如什么是证券投资组合概率集,什么是收益概率分布以及效用函数。
2.解释证券投资组合中的最大预期效用标准。
3.解释什么是风险规避者。
4.解释为什么一个风险规避者一般都会使自己的证券投资组合多样化,以及为什么风险规避者会获得比无风险证券更高的风险酬金率。
5.解释为什么预期效用标准不是运营性的。与此同时,解释为什么这个标准仍然有其重要性。
2003年初,与2001年“9·11”恐怖袭击相关的地缘政治危机随之而来的“反恐战争”,以及生意圈内的不确定情况,都让投资者们很难有投资的勇气。的确《投资新闻7》报道的Merrill Lynch公司对基金经理人的调查,精彩地说明了风险规避的问题,而在这样短时期内能有如此规模的风险规避也着实让人难忘。同时,该报道也表明,尽管基金经理人有很强的风险规避情绪,但是他们中的大部分仍然对将来的收入和经济增长持乐观态度。
投资决策很大程度上取决于预期的投资风险以及风险规避,另外一个重要的决定因素就是投资限制。很多投资者都会遇到形形色色的限制。比如说风险投资(如股票、垃圾债券和衍生证券)中的投入资本量上限,以及社会和环境的屏护(投资应是负有一定社会责任的)。这些限制通过监督员、投资监管、工业中的道德行为准则以及诸如此类的方式而强加于投资者身上。
的确,金融经济学者一般都把投资模型设立为不确定情况下有限制的最优化组合(Constrained Optimisation Under Uncertainty)问题。这个问题由三个因素构成:最优化(Optimisation)、不确定性(Uncertainty)以及限制性条件(Constraints)。投资者尝试努力地在一种以不确定性为特征的环境下,最优化某个(自己的主观)客观功能,而又同时受制于强加在他身上的投资限制。简单来说,在金融经济学者看来,投资就是投资者在他们的预期、目标以及限制都一定的情况下尽可能地选择更加有利的投资策略。为了对这个笼统的研究方法做一个补充,他们常常会使用三个基本概念:描述投资者目的的效用函数(Utility Function);概率分布(Probability Distribution),用以描述投资者对将来投资回报的预期以及这些投资回报能实现的概率;投资组合概率集(Portfolio Possibilities Set),用以描述投资者面对的概率和各种限制。下面我们将更加细致地讨论这些概念。
为了便于展开,对这些概念的论述可以与上文介绍相反的顺序:从投资组合概率集开始到效用函数结束。在讨论完这些概念之后,我们会把这些概念都整合到预期效用标准里去,根据这个标准,投资者们会从众多资产投资组合中选择有最高可能预期值的那个,把这个预期值用效用函数表示出来。最后,用这个预期效用框架帮助我们理解两个重要的经济现象:一是资产投资组合多样化;二是为什么能获得比无风险证券收益率高得多的风险酬金。
7.1 投资组合概率集
假设一个投资者可以选择几种证券进行投资,而这些证券的收益率都不确定,分别用R1,…,Rn来表示。这个投资者选择了某一个资产投资组合,在这个组合中各个证券占有各种各样的比例,这些比例也可以称做投资组合权重(Portfolio Weights)。权重表示的仅仅是对每个单一证券投资的财产量在所有投资资金中的一个比重。在全书中我们都会用w1,…,wn来表示投资组合中各个单位证券的权重。如果投资组合不包括某个证券,那么这个证券在所有投资份额中所占的比重就是0,也就是说wi=0。回忆一下第3章中对“卖空”的讨论,就会发现:卖空就是指一个投资者继续出售自己已经没有所有权的证券。同样的,如果你对一种证券的持有量已经不足了,那么这个证券实际上就会在你的投资组合中占有一个负权重(wi<0),也就是说,你对这个证券的拥有量是负数。一个投资组合的收益率可以用各项单一证券的收益率的加权平均数来表示:
![]()
总的来说,这些组合权重的值并不是任意的,它们是受一些条件制约的。在这些制约条件中,最基本的一条就是一个投资者投资的总额不能超过他/她拥有的全部财产。这个制约条件在数学公式中体现为资产投资组合中的组合权重之和应当为1,或者说,100%。
一个投资者经常会遇到的问题就是卖空,这是不允许的。卖空在实际操作中一般很难实现,因为实际操作中最低保证金量和一些针对机构投资者们设定的显性或隐性的限制会杜绝卖空行为的发生。[1]在数学公式中,可以通过让所有的权重都大于等于0来把卖空行为排除到数学模型之外,也就是说
![]()
此公式中,i的取值范围是1,…,n。在投资组合要遵循的众多限制中,以上所述的仅仅是其中的两个例子。其他这方面的例子还包括某个证券与基本指数间的偏差度大小,或者从长期的证券分配来看,这些限制还包括对单个证券、投资领域以及投资国家、证券类型的限制。此外,在投资对象中还要排除那些涉及烟草、酒精和武器生产及(或)分配的企业。
假设一个投资者可以选择三支不同的股票来投资,这三支股票分别用股票1、股票2和股票3来表示,图7.1表示的是在这种情况下的投资组合概率集。图7.1中三角形OAB的各边即投资行为要受到的制约:一是投资组合中各单支股票的权重之和应该是100%(w1+w2+w3=1);二是不允许有空卖行为w1,w2,w3≥0。举例来说,从图中可以看出,投资组合F中有70%的资金投到了股票1上,有20%投资到股票2上,还有10%投资到股票3上。类似的,投资组合G有60%的资金投资到股票1上,有40%投资到股票2上,股票3无投资。值得注意的是,图中仅表示出了股票1和股票2的权重。因为所有权重之和必然是100%,故而股票3所占的权重就可以通过1-w1-w2得出。组合G中股票3的权重为0,这就可以解释为什么组合G会处在概率值OAB的斜边上了。同时整个组合G又要受到不得卖空的限制(w3=0)。如果我们再给投资者加上第三条限制,让各股票的组合权重只能小于或者等于50%,也就是说,w1,w2,w3≤0.5,那么图7.1中三角形CDE就正好体现了这条限制。请注意,组合F和G在概率集CDE之外。这是因为在这两个组合中,股票1所占的权重超过了50%。与此相对照的是,因为组合H中有40%的资金投资到股票1中,30%的资金投资到股票2中,还有30%的资金投资到股票3中,所以组合H处在概率集CDE中是有道理的。
总体说来,给投资行为强加诸多的限制,降低了投资的可能性,还会让投资者的境况变得糟糕,因为这些规定限制了他们的选择(当然,从整体上看,这些限制措施对于整个社会还是有利的,因为它们防止投资者使用非法或不道德的投资策略来牟取私利)。类似的,解除投资限制就可以扩展投资概率集,进而使投资者的境遇得以改善。
理论联系实际7.1
FT
养老金进入产权投资市场,为经济高涨带来动力
Birinyi联合公司是一家股市研究公司,根据它新近做的一项研究显示,在未来的10年里,用养老基金进行的产权投资会有一个“非同一般的增长幅度”,而这些新增投资中的大部分会流向国外市场。这项名为“养老金改革与全球产权市场”的研究表明:分析家们正试图量化当前41个国家推行养老金改革对于成熟股市以及正在发育的股市带来的影响。如果这些结论正确的话,在更长的时期内,机构投资者很可能会在支持产权价格以及弥补前两年的损失方面发挥更加重要的作用。他们同时也暗示,“世界”范围内的投资组合会更快地向更平静的方向转变,养老金的跨国境投资进程也会跟着加快。
该研究指出,在20世纪90年代的10年中,全球养老基金证券平均每年增加15%,从46000亿美元增加到159000亿美元。与此同时,养老基金的产权持有量由16000亿美元增加到80000亿美元,或者说由占总体证券量的35%增加到51%。到1998年底,养老基金的持有量在全球产权市场总资本量中的比重由1990年的17%上升到27.4%。但是在1999年,由于网络经济过热和市价的大幅上升,这个比重回落到了22.9%。达到这些增长的主要是养老金市场的三大巨头——美国、日本和英国,加在一起就占到了全球证券市场的80%还要多。单单美国就占到了世界证券市场60%的份额。从1995~1999年,美国养老基金证券年均增长率为21%,英国是16%,日本也达到近10%。此项报告预计由于以下三大因素的影响,养老基金持有量为期10年的增长势头在未来10年之内还会继续保持。
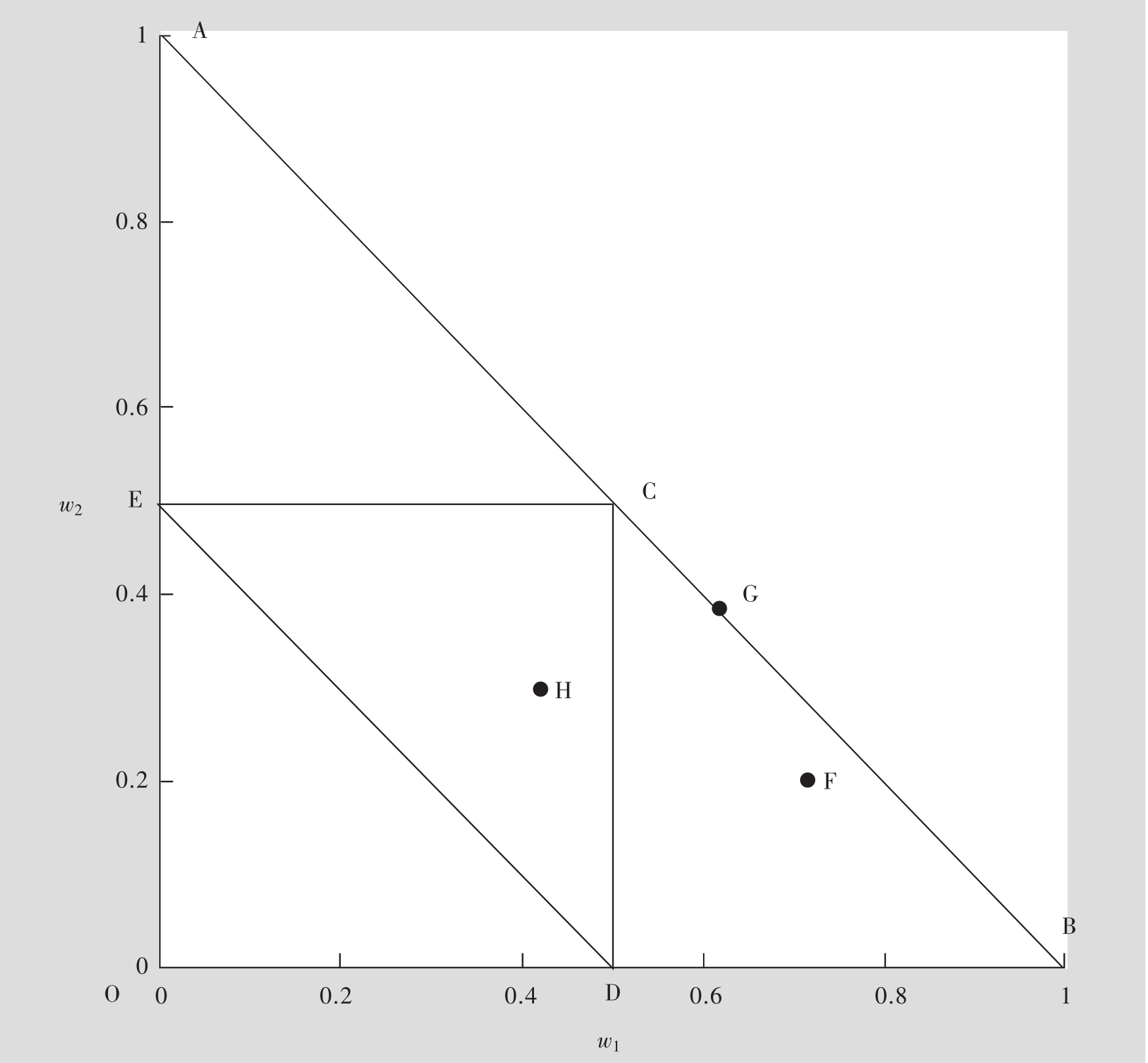
图7.1 两组投资限制下的投资组合概率集示例
首先,就是养老金改革。自20世纪90年代中期以来,欧洲、拉美以及亚洲的各国政府已经采取政策措施,逐步以“有充足资金保障的养老保障方案”来完善或代替原来的养老保障系统,因为以前以“能劳动就得参加保障”为特色的旧体系没有充足的资金支持。在这些国家的改革中,大多数国家的政府都在沿用美国的私人储蓄账户方式,比如说个人退休账户和401(K)计划。瑞典在东欧诸国中是推行养老金改革最快的一个国家,该国政府正在推行一项新的养老保障系统。这个新系统以强制性个人退休账户为基础,有望在推行的第1年里向产权资本基金注入160亿美元的资金。在德国,新的法规将在今年内促成建立一套以税收盈余为基础的养老金账户体系,通过这一新体系,养老金存储额有望在2008年之前新增300亿美元。中国的养老金计划同样是在财政赤字很严重的情况下推行的,将来这个计划很有可能面临更严峻的形势,因为会有更多的国有企业在经济改革中倒闭。为了应对这种情况,中国政府正在考虑推行一系列的改革来解决当前养老金体系问题,包括建立起一套以“强制雇主存储养老基金”为基础的养老金计划。如果这一揽子计划得以推行,中国的养老基金证券有可能在2030年之前新增16000亿美元。
与此同时,由于政府发行的中期债券回报额的降低,投资者们正越来越容易接受与产权投资相伴的风险。这样,对于用养老基金购得产权所有权的限制也就慢慢地放松了。在欧洲,更为宽松的投资限制和投资者试图多样化的融资组合,已经给股权分配带来了巨大的影响。如此一来,产权投资中这种标记性的趋势在欧洲就更为明显了。此外,世界范围内的政府储备基金都在把证券分配从政府债券向产权投资倾斜。这个倾斜当前正在日本发生,该国在2010年之前将有900亿美元的资金从政府债券流向产权投资市场。韩国、加拿大、爱尔兰、法国以及比利时都有相似的情形。
最后,随着金融市场的成熟和风险多样化带来的好处正在更大程度上被人们认可,政府决策者们正在重新考虑对外国养老金投资设定限制。这个趋势在爱尔兰、比利时、西班牙、冰岛尤为明显。在美国,一项对200个最好的养老金进行的调查显示:这些养老金计划中外国产权持有量所占的比重仅在1998~1999年一年间由12.1%上升到了14.2%。
Birinyi联合公司指出:“以养老基金购得产权所有权的现象正在增加,这有可能会对已成熟的和正在形成的资本市场产生影响,而这种影响有可能会持续一个较长的时期。”
资料来源:保罗·泰勒:《养老金进入产权市场,为经济高涨带来动力》,《金融时报》2002年3月5日。
7.2 概率分布
对大多数有价证券而言,将来的收益率是不确定的。也就是说,可能的收益率结果不止一个,但也有例外,这就是美国财政短期国库券(也就是所谓的T券)。在较长的一段时期内,T券的收益率的确是改变的,但是,当某一个人买了某个时期的T券,如果他/她能在国库券到期之日再卖出的话,所赚取的收益额是固定的(当然以上所说的要忽略通货膨胀因素或在美国爆发一场政治革命的可能性,才能成立)。同样,因为T券是一种短期证券,利益改变不会很显著地影响到国库券到期前的价格。因此,学者们通常把T券称做无风险证券(Riskless Asset),将其收益称做无风险利率(Riskless Interest Rate)。
其他的有价证券,比如说股票、长期债券、各类期权、房地产投资以及其他诸如此类的投资,将来的收益率都是高度不确定的(参见第2章第4节有关股票及债券投资者可能预见的各种风险的论述,及参见第6章第5节关于此类证券收益率演变的论述)。实际上,如果这些证券没有风险,那么它们的收益率水平应该与T券一样,否则投资者们就会抛售收益水平最低的债券,把投资资金转向收益水平高的。为了便于理解这个道理,假设有A、B两种证券,每一种的市场价格都是100美元。假如确切地知道A证券将来的市场价格为110美元,B证券将来的市场价格为120美元,且这两种证券都没有股息或利息可赚,市场是平衡的吗?结果并不是。既然A证券和B证券的现价都同为100美元,且B证券将来肯定能获得比A证券更高的市场价格,那么,一个现在持有A证券的投资者应当卖掉A证券以购进B证券。这样一来,这个投资者不用做什么投资就肯定可以多赚10美元,也就是B证券预期市价与A证券预期市价的差:120美元减110美元。这种贸易策略叫套利(Arbitrage),指的是不用承担风险也不用投资就可以获利的现象。套利行为会使A证券的市场价格降低(因为市场上将会供给很多A证券),同时也会让B证券的市价提升(因为市场上将会需求大量的B证券)。这种状况要一直持续到这两种证券收益率都达到某个相同的特定值为止。因此,股票和债券从历史上来看总有比无风险利率更高的收益率,这一事实从一个角度证明了股票和债券是有风险的。
从较为正规的角度而言,我们必须得区分“不确定性”和“风险”这两个概念。如果投资者们知道每个可能出现的结果有多大的概率,那么他们面对的是风险(Risk)。如果投资者们并不知道每个可能出现的结果各有多大的概率,那么他们面对的是不确定性(Uncertainty)。[2]请注意,不论是不确定性还是风险,都意味着将来可能的取值都不止一个。客观概率(Objective Probabilities)指的是可以知道的实际概率(比如说在抛硬币实验中哪面向上的概率)。在投资者实际的投资决策中,很少有确切知道真正的概率是多少的。一般而言,为了评估某公司股票未来某个收益率出现的概率,投资者可以先收集一组该股票历史收益率的数据;或者收集一组与该股票有可比性的证券(比如说,同产业同等规模公司的股票)在各历史时期里收益率的数据。以这些数据为基础,投资者就可以预测收益率出现的概率了。同时,他/她也可以根据该公司的相关信息,以及未包括在过去收益水平的产业及经济情况,对已评估的历史概率作出修正。这样经过修正得出的概率称为主观概率(Subjective Probabilities)。因此,就算是客观概率未知,投资者仍然可以把主观概率与某证券各种未来可能出现的结果联系在一起。如此一来,他/她面对的情况就可以用风险而非不确定性来定义了。既然一个投资者经常可以将主观概率与各种各样可能出现的结果联系起来,在本书余下的章节里,“风险”和“不确定性”这两个术语就可以互相换用,以表明有多种可能的结果出现。
投资者对未来可能回报的主观期望以及这些收益实现的概率都可以用一个概率分布(Probability Distribution)来描述。概率分布就是一个数理函数,它可以给出一个随机变量或一组随机变量出现某种结果的概率。证券收益概率分布有时也称收益产生过程。一个单变量概率分布(Univariate Distribution)是单独的考虑单个随机变量可能出现的结果。相反的,一个多变量概率分布(Multivariate Distribution)则是考虑几个随机变量的联合分布情况。
在选取投资组合的时候,考察所有可能投资的证券有什么样的概率联合分布是很重要的。单变量分布只是孤立地考察一个证券可能出现的收益情况。与此相对照的是,多变量概率分布可以一起给出所有证券可能有的收益结果。为了衡量评价一个由多个证券构成的投资组合有什么样的概率分布,我们必须得考虑联合分布。比如说,如果某个单一证券很可能在其他证券震荡时也随之震荡,这个证券就能给投资组合带来更大的多样化可能性。因此,为了衡量投资组合中的单一证券,我们得在了解它的概率分布的同时,解释它对该组合中其他证券的依存度。单变量概率分布不能给出投资组合中各证券间相互依存的信息,多变量分布则确实能给出这些信息。
此处我们将把多变量概率分布表示成一组有m个不连续的随机事件。比如说,我们生活的世界中可能有的一个随机事件就是:一方面美国经济在扩张,而世界其他地方的经济却处在一种停滞状态。与这些随机事件相联系的是一组概率P1,…,Pm。这些概率的值都是正数(P1≥0),它们之和为1,或者说是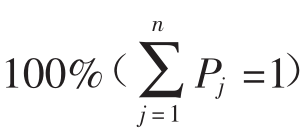 1。[3]在第j个随机事件中,各证券的收益率用R1,j,…,Rn,j表示。[4]
1。[3]在第j个随机事件中,各证券的收益率用R1,j,…,Rn,j表示。[4]
图7.2展现了以股票1、股票2、股票3三支不同股票为例的概率分布。在这个例子中,有10个不同的随机事件,每个事件的概率相同都是10%。图7.2(a)是这三支股票的多变量概率分布,而图7.2(b)则用直方图表示了每支股票的单变量概率分布图,图7.2(c)表示了每两对股票之间的相关度(如股票1和股票2、股票1和股票3、股票2和股票3)。[5]
图7.2(a)包含两种用来归结(单变量)收益分布的一般统计数据:均值(Mean)与方差(Variance)。预期收益值(Expected Return)或者说平均收益值(Mean Return)是用来计量收益分布的集中趋势的,或者说是用来计量分布在什么地方集中的。[6]第i个证券的收益均值是这个证券在所有可能的随机事件中获得的收益的加权平均数:
![]()
在这个公式中,E表示期望操作者注意E(Ri)计量的是预期收益,也就是说它指的是未来的收益。与此相对照的是,前一章所讲的是样本均值Ri,计量的是过去的收益,它是从历史收益中抽样计算出来的。未来区分这两个统计指标,一般把E(Ri)称做总体均值(Population Mean)。在这个例子里,所有三支股票的均值都是一样的(0.080)。
总体方差(Population Variance)表示的是集中趋势周围的离散程度,用来计量风险高低。[7]可能收益的方差用σ2表示,σ2的算法如下:
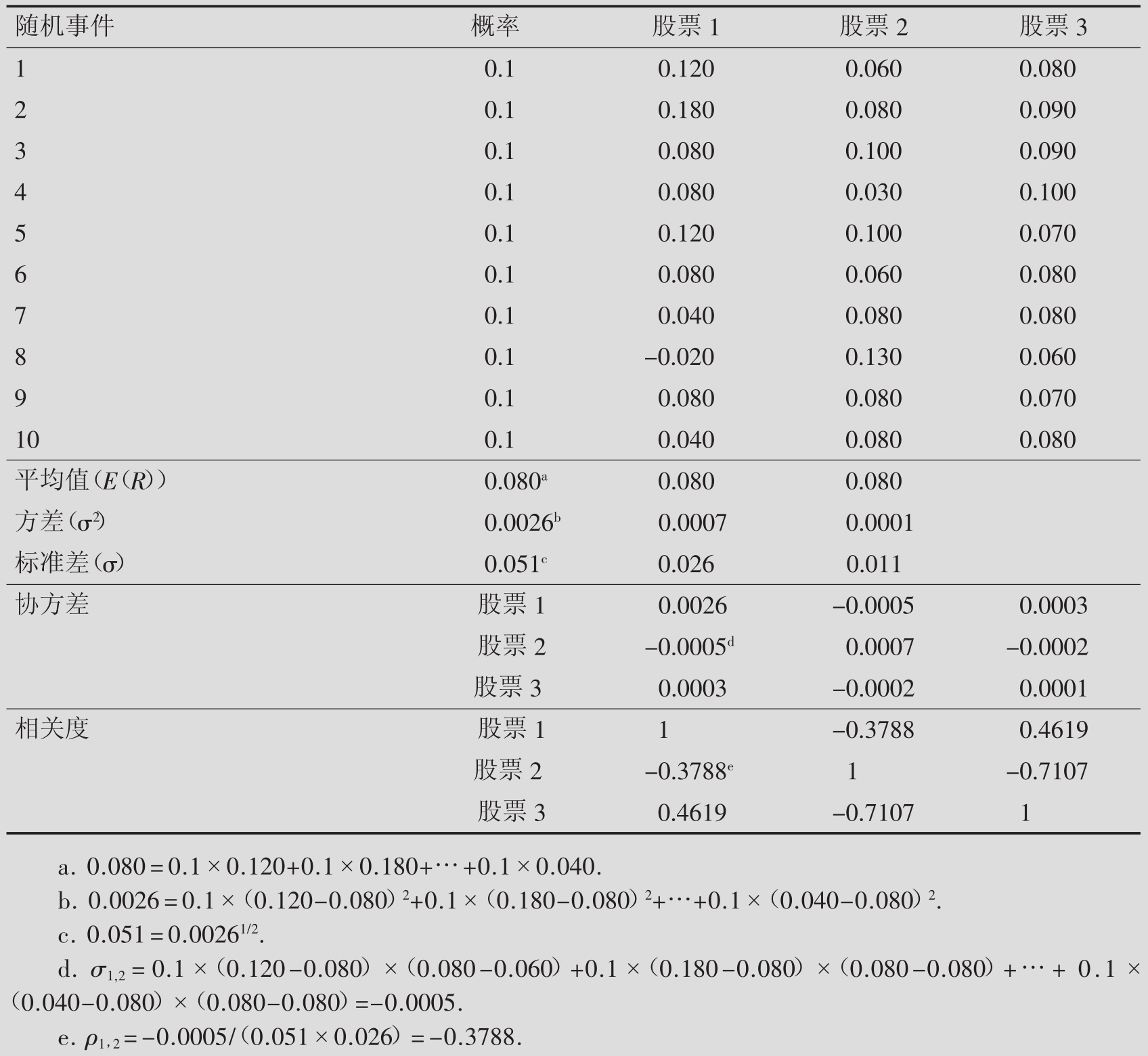
图7.2 (a)股票1、股票2、股票3的多变量概率分布
![]()
因此,这个方差就是所有概率之和乘以均值的平方差所得的积。正如可以从这个公式看出来的,不确定性是用与均值的偏差来计量的。这样,不确定性越高,方差越大。有时,如下所示的一个等效表达式可能会更方便:[8]
![]()
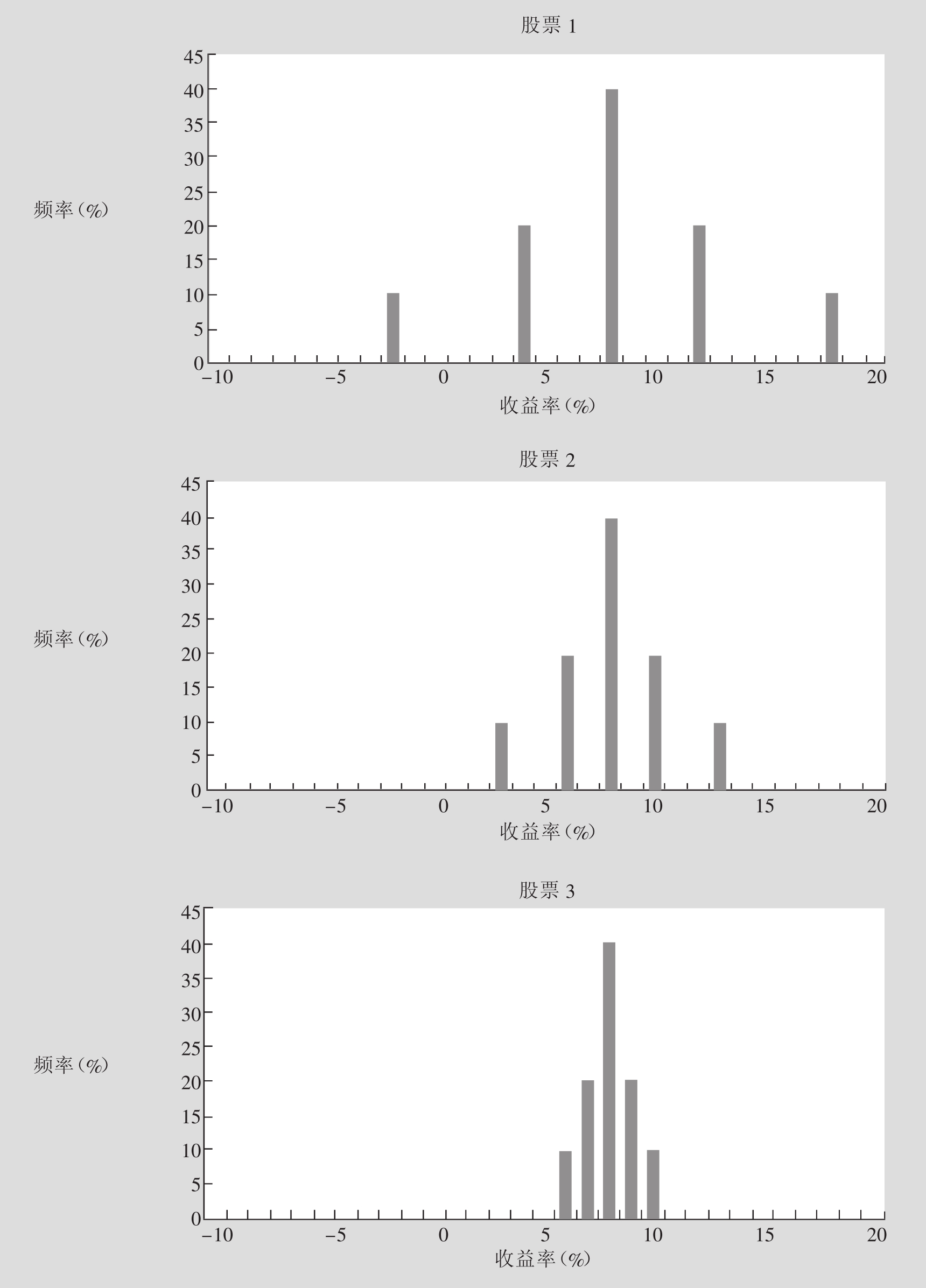
图7.2 (b)股票1、股票2、股票3的单变量概率分布
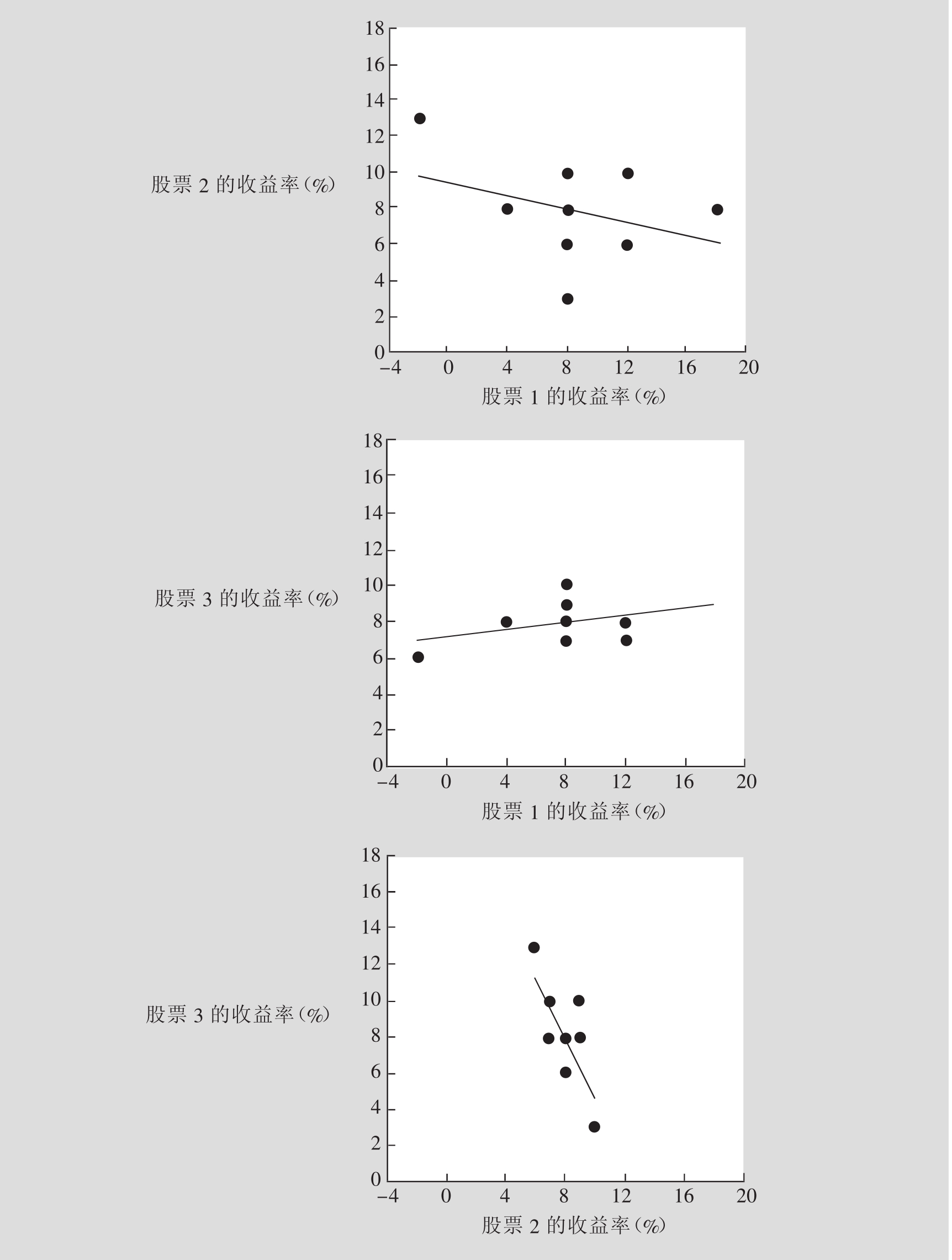
图7.2 (c)股票1、股票2、股票3间的相关度
由于收益率以百分数或美元金额来表示,方差的单位就是百分数的平方或者美元金额的平方。鉴于这些术语可能难以解读,经常把方差的平方根,也就是σi,称做总体标准差(Population Standard Deviation)。这个计量工具是用百分比或美元来表达的。注意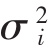 计量的是预期风险,即它描述的是将来的情况。与此相反的是,样本方差
计量的是预期风险,即它描述的是将来的情况。与此相反的是,样本方差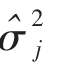 计量的是既往收益的离散性。在此例中,股票1的方差最大(0.0026),股票3的方差最小(0.0001)。
计量的是既往收益的离散性。在此例中,股票1的方差最大(0.0026),股票3的方差最小(0.0001)。
再次说一下,单变量分布只提供单个股票的风险和收益信息。这些信息对一个只想单独购买上面三支股票中任何一支的投资者来说就已经足够了。然而,一个想要同时投资三支股票的投资者,则还需要这三支股票间的相互依存度的相关信息。第6章已经介绍了两个常用来归结一对随机变量间依存度的统计工具:协方差和相关系数。本章说明了这些统计工具能如何从历史数据中计算出来。由此得出的 和
和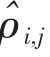 就是样本协方差和样本相关系数。与此相反的是,图7.2(a)包含了总体协方差(Population Covariance)和总体相关(Population Correlation),这二者的计算方法都和未来的收益分布相联系。
就是样本协方差和样本相关系数。与此相反的是,图7.2(a)包含了总体协方差(Population Covariance)和总体相关(Population Correlation),这二者的计算方法都和未来的收益分布相联系。
第i个证券至第j个证券间的总体协方差可以用下面给出的数学公式求得:
![]()
这个等式表明,协方差是一个表示对均值偏离程度大小的预期值。如果两支股票的收益都同时高于或低于均值,那么它们互相运动的结果就是一个正值,所以协方差也会是一个正数。然而,如果一支股票的收益高于均值,而另一支股票的收益却低于均值,那么它们的结果就会是一个负数。如果这种情况发生,那么协方差也就会变成一个负数。有时以下的这个公式会更方便:[9]
![]()
类比第6章中对样本协方差的讨论,我们就知道,某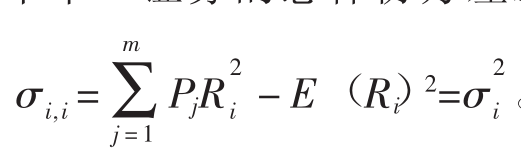 个单一证券的总体协方差就是它本身的总体方差。由公式7.6a,用i代换s就可以得出:。同时,σi,s=σs,i。这样,证券i与证券s的协方差就等于证券s与证券i的协方差了。
个单一证券的总体协方差就是它本身的总体方差。由公式7.6a,用i代换s就可以得出:。同时,σi,s=σs,i。这样,证券i与证券s的协方差就等于证券s与证券i的协方差了。
图示7.2(c)显示了所有这三支股票收益率的情况,同时,它们之间以协方差计量的依存度也可以从中看出来。图中每一个点都表示一对股票在某个特定态势下的收益。很明显,股票1和股票2之间呈现出一种负向移动的关系,或者说它们之间存在负的协方差。在这两支股票中,当其中一支走势较好的时候,另一支在大多数情况下都走势较差,反之亦然。比如说,在第八号态势中,股票1的收益率为负的2%,股票2的收益率则达到正的13%。反过来,当股票1的收益率较高时,股票2的收益率则普遍很低。注意,在你从左看到右的时候,会发现表示依存关系的图像逐渐向坐标系的下方靠拢。这种向下靠拢的图像是负协方差的特征。与此相反,股票1和股票3两者之间则呈现出正协方差的特征。
协方差是正值还是负值,暗示同一组的单个证券不是走势一致就是走势相反,但是正协方差和负协方差却无法表示这个证券组合中各单个证券间依存性的强度。用协方差除以各单个证券的标准差,就可以判定它们之间的依存性或者说它们的相关程度。这样计算出来的结果称之为总体相关度系数(Population Correlation Coefficient):
![]()
与抽样相关度系数一样(有关抽样相关度系数的论述参见第6章),总体相关度系数的取值范围是在-1~1之间,同时它也可以直接与不同的证券对进行比较。比如说,股票1和股票2的收益率相关度系数是-0.3788,而股票2和股票3两者之间的收益率相关度系数是-0.7107,所以,我们可以说,股票2和股票3两者之间的负相关度强于股票1和股票2之间的负相关度。在图示7.2(c)中,直线旁的小离散点群反映了股票2和股票3两者之间的强相关度,而股票1和股票2之间较弱的相关度则通过直线旁边更多的离散表现出来。如果某两支股票的收益率之间存在完全的正相关,那么它们的相关系数是+1;如果两支股票的收益率之间存在完全的负相关,那么它们的相关系数就是-1。如果两支股票的收益率毫无相关(也就是说无相关性),那么此系数的值为0。如第6章所述,某个投资组合中的单一证券与其自身的总体相关系数值为+1,因为: ρi,i=。同样,ρi,s=ρs,i,也就是说,证券i和证券s之间的相关系数与证券s和证券i之间的相关系数是一样的。
ρi,i=。同样,ρi,s=ρs,i,也就是说,证券i和证券s之间的相关系数与证券s和证券i之间的相关系数是一样的。
正态分布
图7.2中所示的是:在可数的随机事件(m=10)中,概率分布的情况。这样的分布被称为离散分布(Discrete Distribution)。与此相反的是,我们不能计量一个连续分布(Continuous Distribution)里可能出现的结果有多少。对这样的一个分布,不能用一组可数的集合R1,…,Rn来描述所有可能出现的结果,因为(R1+R2)/2这个结果很可能会出现,但是却没有包括在上面那个集合中。这就暗示了每个可能出现的结果都只有无限小的可能性。与此相关的,连续分布一般都用它们的概率密度函数(Probability Density Functions)来表示。某个结果的概率密度,就是经过重新换算后,在概率密度函数的图像中面积为1的那个概率。由于重新换算的缘故,概率密度表现的不是绝对的,而是相对的。比如说,如果R=0的概率密度是0.397,而R=1的概率密度是0.242,这并不是意味着R=0有39.7%的概率成为现实,或者R=1有24.2%的概率成真。相反,这只是说R=0的概率(这个概率本身就是无限小的)是R=1的概率(这个概率本身也是无限小的)的39.7/24.2= 1.64倍。
大部分情况下,投资组合中各项单个证券的收益分布可以用离散分布来模拟,因为我们常常并不需要不计其数的态势。同样,态势的数量一般都很大,以至于由此而来的信息处理和运算负担过重。特别是当考虑到成千上万个证券时,这个问题将会变得尤其严重。在这种情况下,某些连续分布会比较有用。因为它们可以用几个几何图形参数描述出来。投资学著作中最重要的连续分布就是双参数正态分布。[10]这个分布在均值—方差分析(Mean-Variance Analysis)中有着重要的地位(关于均值—方差的分析可参见第8章的相关内容),而均值—方差分析又是很多证券定价理论和实际投资工具的基础。
R的正常概率密度可以用以下公式给出:
![]()
在这个公式中,E(R)表示均值,σ表示标准差,exp表示幂,即底数的e次幂。
图示7.3(a)表示的是三个(A、B和C)正态分布的例子。与这三个例子一样,正态分布就总体而言,具有一些特定的属性:
■该分布完全以其均值和方差(其平方根也就是标准差)为特征。比如说,A分布对应的是E(RA)=0和σA=1。B分布有同样的集中趋势(E(RB)=0),但是它的标准差却比A的标准差高(σB=2)。很明显,B分布比A分布更加分散。最后,在C分布中,其均值是E(RC)=2,方差为σC=2。这个分布除了它的集中趋势比B分布更高以外,其他方面都与B分布一样。A分布(均值为0,有单位方差)被称为标准正态分布(Standard Normal Distribution)。其他的正态分布都是这个标准正态分布的简单线性变形或转化。更具体地说,如果一个随机变量遵循一个平均期望为E(R),标准差为σ的正态分布,那么这个标准化后的随机变量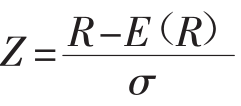 (或者说Z分数)就也会遵循标准正态分布。
(或者说Z分数)就也会遵循标准正态分布。
■正态分布可能出现的结果,范围在+∞~-∞之间,所以正态分布曲线的两个尾端向左向右都无限延伸。
■分布曲线以均值尾轴,左右两边对称。E(R)+x这一结果出现的概率密度和E(R)-x这一结果出现的概率密度完全相同。正态分布曲线的这种对称性可以从图7.3(a)中看出来。同样,式7.8也能体现这种对称性。这个公式表明,R=E(R)+x和R=E(R)-x在(fR)中的取值是一样的,在两种情况下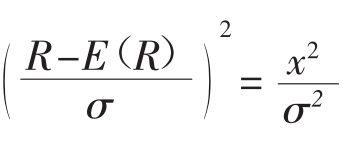 都成立。
都成立。
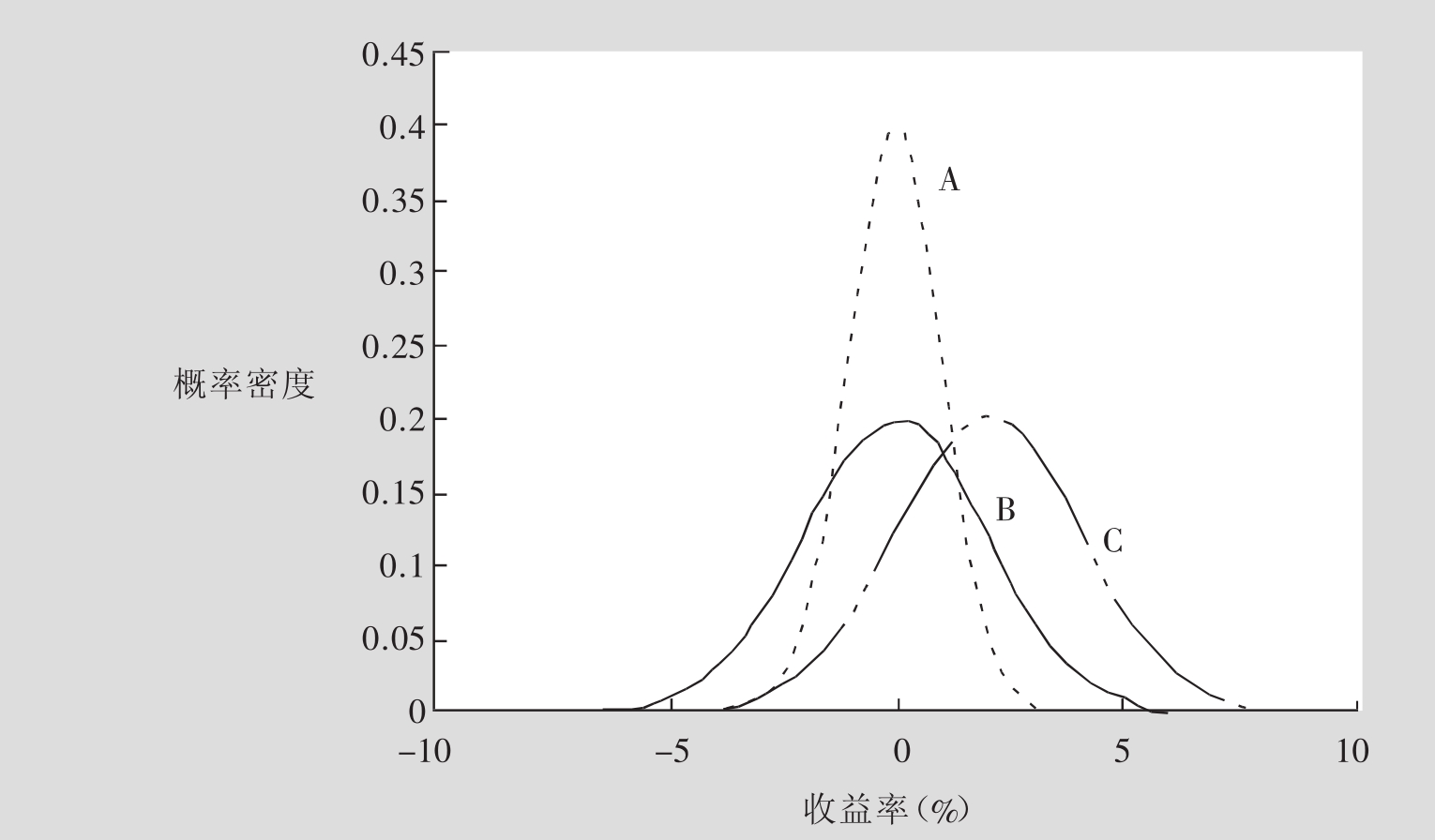
图7.3 (a)正态概率密度函数
■某个结果距均值越远,分配到它上面的概率密度就越小。此外,对于与均值相差较小的变量,其概率密度就会加速下降;而对于与均值相差较大的变量,其概率密度就会减速下降。这样一来,概率分布的曲线就成为一个钟形。
再次说一下,对一个连续型随机变量而言,每个可能出现的结果,概率都是无穷小的,我们一般也不会对这样小的概率感兴趣。相反,通常更愿意知道一个变量在某个范围内出现的概率,以及这个变量比某个关键值低或超出某个瓶颈的概率。为此,就需要考虑积累分布函数(Cumulative Distribution Function)。积累分布函数可以给出一个随机变量取一个小于或等于某个值的概率。从数学的角度而言,它在概率分布函数的图像中表示的是,从负无穷到那个特征值之间的面积。回忆一下,密度函数所有的面积(从负无穷到正无穷)是1,因此大部分的特征值在积累分布函数中的值也就接近1。图7.3(b)展示了图7.3(a)中那三个正态密度函数的积累分布函数。对A分布而言,收益低于-1%的概率是15.9%。对B分布而言,因为它的方差较大,其收益低于-1%的概率是30.9%。对C分布而言,因为它的均值较大,出现这种情况的概率是6.7%。
不幸的是,还没有完善的解法可以用来计算积累正态分布函数的概率。尽管如此,还是可以通过电脑模拟技术或者数值积分的方法,得到一个近似值。附录7包含了一张标准正态分布概率的表格。如果一个正态随机变量有非零均值或非单位方差的话,这个变量的值就可以通过把它转变成一个标准随机变量而得到。为了达到这个目的,我们又要计算标准化分数Z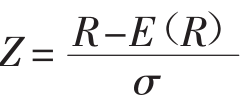 =。所以,如果某个证券遵循C分布,而C分布的E(R)=2,σ=2,那么,收益低于R=-1%的概率就可以通过标准化分数公式求得为:
=。所以,如果某个证券遵循C分布,而C分布的E(R)=2,σ=2,那么,收益低于R=-1%的概率就可以通过标准化分数公式求得为: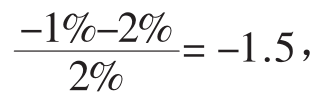 然后在附录7所示的标准正态分布表格中寻找与此值相对应的概率。在这个例子中,查得的概率结果是0.0668,也就大约是6.7%。
然后在附录7所示的标准正态分布表格中寻找与此值相对应的概率。在这个例子中,查得的概率结果是0.0668,也就大约是6.7%。
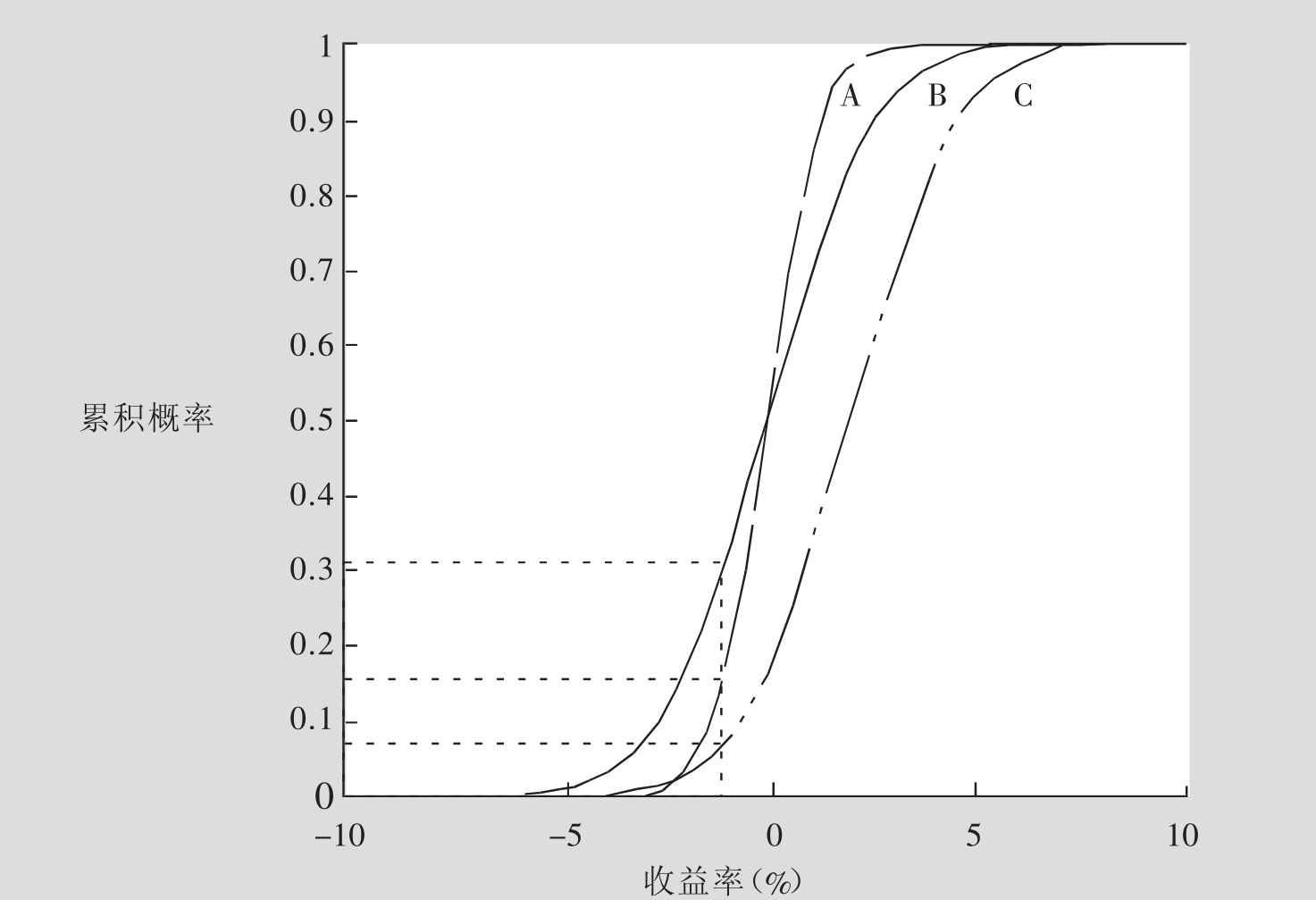
图7.3 (b)累积正态分布函数
注意,上面所讲的例子都只是单变量正态分布。要描述多个正态随机变量的联合分布情况,就得考虑多变量正态分布。除了单个变量的均值和方差,多变量正态分布同样能描述单个证券间的依存度。就正态分布而言,协方差用来计量相互间的依存度(也有用相关系数来计量的,相关系数是协方差的一个标准化版本)。因此,多变量正态分布不仅是用所有证券变量的均值和方差来描述的,还同时用所有证券间的协方差(或相关系数)来描述。
有趣的是,正态分布中,两个或多个随机变量的加权平均数也呈正态分布。因此,当一组证券变量有一个(联合)正态分布时,由这些证券变量构成的投资组合也呈正态分布。第8章将讲述如何由单个证券变量的均值、方差和协方差(或相关系数)计算出一个投资组合的均值和方差。
7.3 效用函数
投资者们的目标常常用效用函数来描述。效用函数可以给所有可能出现的投资组合收益分配一个效用值。在全书中用u(R)表示与收益R相对应的效用值。这个效用值计量的是与收益R相对应的主观满足感。主观满足感可能会来源于几个不同的方面。这种满足感最基本的来源,就是部分或全部卖出投资组合后,可能带来的追加商品或服务消费(或者与相联系的社会地位)。同样,一些投资者也可能从投资博弈的兴奋感,或者超越其他投资者所处的境遇带来的感觉中获得满足。
效用函数总体而言有以下四个重要的特征:
■效用是逐渐增加的,也就是说收益水平越高,投资者就越满足。原因很简单:因为更高的收益水平让他/她有能力支付更多的消费开支。就算投资者不想追加消费,他/她也可以把这些额外收入给他/她的亲属,或者把这些钱捐献给慈善事业。换言之,边际效用(Marginal Utility),或者说从一个额外收益中获得的额外满足感总是一个正值。效用函数的图像是凹的,也就是说,效用函数的图像向收益值轴弯曲。[11]
■换言之,边际效用水平是渐渐降低的。[12]也就是说,随着收益水平的升高,投资者会变得更加富有,但是从单位收益中获得的满足感的增加值则会降低。效用函数的图像之所以是凹的,是因为消费者一般都是先满足他的最基本的需求,而每个单位的增加财产都会用来支付不那么关乎生存的商品和服务。
比如说,如果你知道毕业后的年薪将由3万美元翻一番,达到6万美元,这是否意味着个人的满足感也会翻一番呢?答案很可能是否定的。你必须用前一个3万美元来买最重要的商品和服务(比如说,食品、服装和住房),而后一个3万美元则用来支付不那么重要的商品和服务(比如说,1辆车或1次度假)。因此,工资提高会增加满足感,却不会使这个满足感翻倍。换一种说法,如果在一顿丰盛的午餐后,再来一次有5道菜的丰盛晚宴,那么这顿晚宴带来的满足感,一定还不如在饥饿时享用同样的丰盛晚宴带来的满足感那么多。
正如我们下面要看到的,逐渐降低的效用水平一般来说,都会暗示投资者的风险规避倾向。如果投资者面前有两个收益水平相同,但是风险水平不同的投资组合,投资者肯定会选择向那个风险水平低的投资组合投资。另外一个高风险的组合会有更大的可能,获得高收入,也同时有更大的可能遭受损失。如果投资者亏了钱,他/她就得牺牲一些商品或服务,而这些比如果赚钱就能支付的商品或服务要重要得多。这又一次因为投资者得先满足他/她的生存需要。总之,亏钱的痛苦比赚取同等数量的钱带来的快乐要大得多。这样的结果就是,投资者会更加喜欢风险最低的那个选择,也就是说他/她采取了风险规避措施。换言之,边际效用水平逐渐降低的投资者不要蜂蜜(较高的收益),并不是因为他们不喜欢蜂蜜,而是因为他们知道他们可能因此而被蜂蜇!效用函数图像的弯曲度,或者说边际效用水平降低的比例,决定了风险规避的水平。
■不同的投资者有不同的效用函数,在众多因素中,这些函数决定于诸如投资者财产、收入、教育程度和年龄这样的因素。比如说,如果一个中等收入的投资者,亏损了占他/她财产一定份额的资金,那么他们也许就得放弃一些关乎生计的基本商品或服务(比如说,出卖住房,或者削减食物和衣物支出)。与此相反的是,一个有雄厚资金的投资者在亏损了相同份额的财产时,可能就不会那么痛苦,因为他/她还可以满足自己最基本的生活需要。类似的,某个投资者的效用函数会随着时间的推移而改变,人生的不同阶段或经济形势改变时,都会有不同的效用函数。
■某个特定投资者在某个特定时间内的效用函数也不是独一无二的。实际上,如果我们在效用函数中加入一个常量,以及/或者以一个正常量乘以效用函数,就可以得出刚好与所有可选项相同的排序。[13]由于这个原因,加上效用函数是与不同投资者或不同时间点相对应的,因而我们不能直接比较效用水平和由不同效用函数给出的边际效用值。
图7.4(a)表示了两个效用函数的例子,这两个效用函数也许是两个投资者的,或者就是同一个投资者在两个不同的时间点上的。第一个效用函数用uA(R)=1-exp(-6R)给出。这种效用函数被称为负指数效用函数。指数-6决定了效用函数图像的曲度(因此也决定了投资者风险规避的水平)。如果我们用一个更极端的数值,比如说-10,那么函数的凹曲程度就会加大。与此相对照的是,一个不那么极端的指数值,比如说-2,会让函数的凹曲程度变小。第二个效用函数是线性的,其表达式是:uB(R)=10R。图7.4(b)表示的是与这些效用函数相联系的边际效用函数,边际效用函数通过求效用函数的一阶导数得出。在第一个效用函数中,边际效用或者u′A(R)=6×exp(-6R)是逐渐下降的。[14]与此相对照的是,第二个函数的边际效用也就是u′B(R)=10是一个恒定不变的值。[15]
7.4 预期效用标准
至此,我们已经讨论了三个重要的投资构成因素:概率集、概率分布以及效用函数。预期效用标准把这三种构成要素都结合到一条决策规则中了。[16]具体而言,预期效用标准陈述的是:投资者会选取一个能给效用函数带来最高可能预期值的投资组合。预期效用就是各种情况下,投资组合收益之效用的加权平均数,这个公式里每种可能的情况都是其概率的加权:
![]()
因此,期望效用规则可以归结成如下的表达式:
Maxmise E(u(Rp))
以上表达式遵从所有关于投资权重w1,…,wn的投资限制。
表7.5及三个图示中描述的投资元素说明了这些投资规则:图7.1中描述的那两组概率集(其中一组是无卖空行为下的概率集,另一个是在没有卖空行为且投资权重为50%时的概率集),图7.2中描述的概率分布,还有图7.4中描述的两个效用函数(其中一个效用函数是风险中性的效用函数,另一个是风险规避的效用函数)。
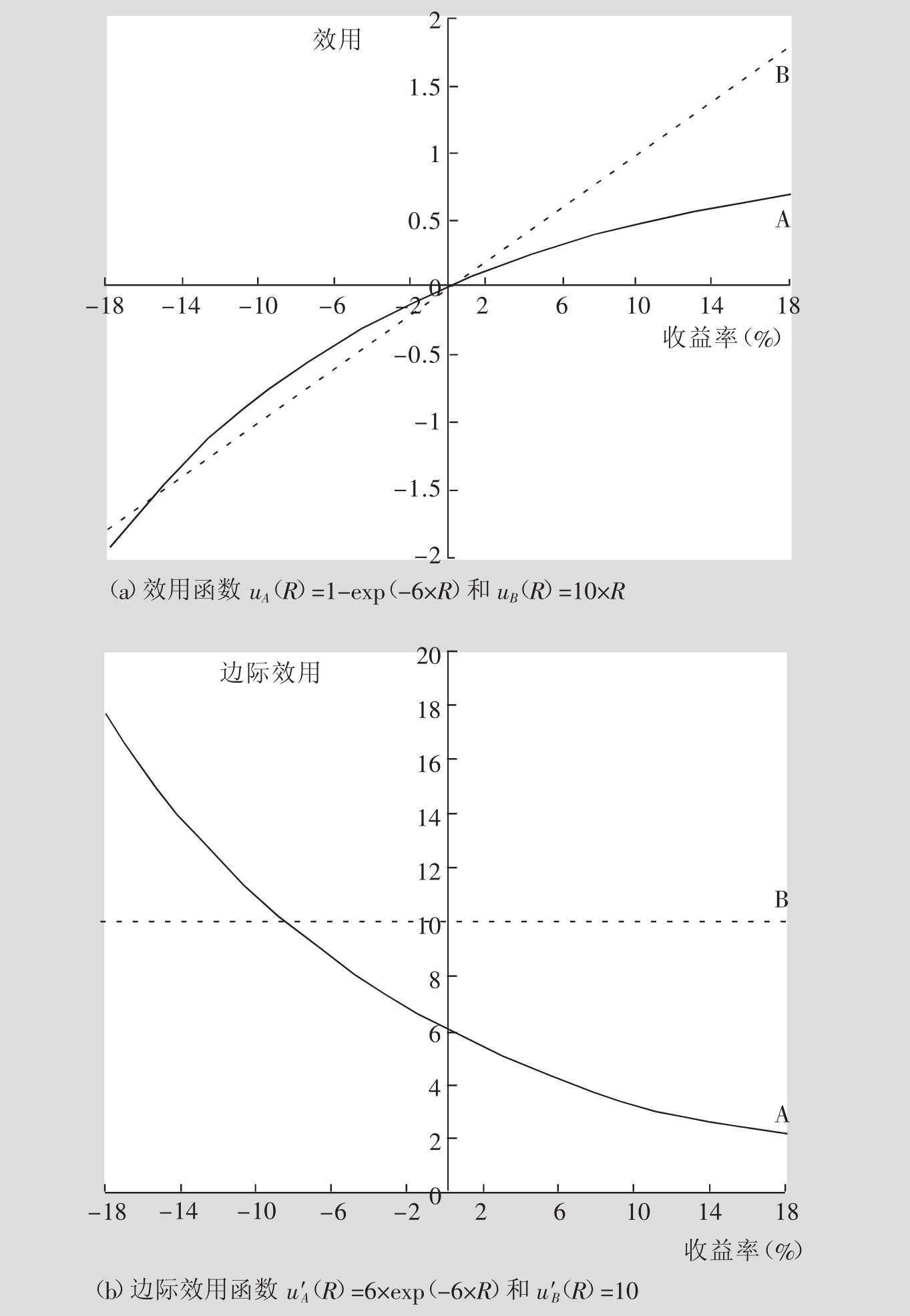
图7.4 效用函数及边际效用函数示例
表7.5中(a)~(c)诸部分给出了与股票1、股票2、股票3中投资相关的预期效用。这些预期效用是第二列中所有概率之和,在第四和第五列中的预期效用分别对应图7.4(a)中的那两个效用函数。从弯曲的效用函数图像(效用函数A)来看,股票1的预期效用最低,而股票3的预期效用最高。出现这种情况的原因很简单。回想一下。图7.2(b)中显示出,其中所有的股票都有相同的预期值:8%,尽管如此,股票1的离散程度最高,而股票3的离散程度最低。这样的结果再一次表示,亏损带来的痛苦要远比赚得等量收益带来的乐趣强烈得多,因为投资者首先得满足他们最根本的生存需要。举例来说,从表7.5(a)中,我们可以推断,8%的收益率对应的效用值为0.381,而如果增加4%的收益率(这样一来收益率达到12%),这个效用值就会增加0.132(0.513-0.381)。尽管如此,如果抽去4%的收益率(这样一来收益率降至4%),[17]效用值就会降低0.168(0.381-0.213)。这样,投资者就会采取风险规避(Risk-averse)措施。在其他条件相当的情况下,他/她会更喜欢均值离散度最小的那个选择。[18]与此相对照的是,就线性效用函数(效用函数B)而言,三支股票的预期效用水平都一样。一个投资者更倾向于选择不确定风险(Risk-neutral);股票的投资者只以预期收益为基础来作决定,他/她对有相同均值的各个备选投资项不感兴趣。
表7.5 预期效用的计算
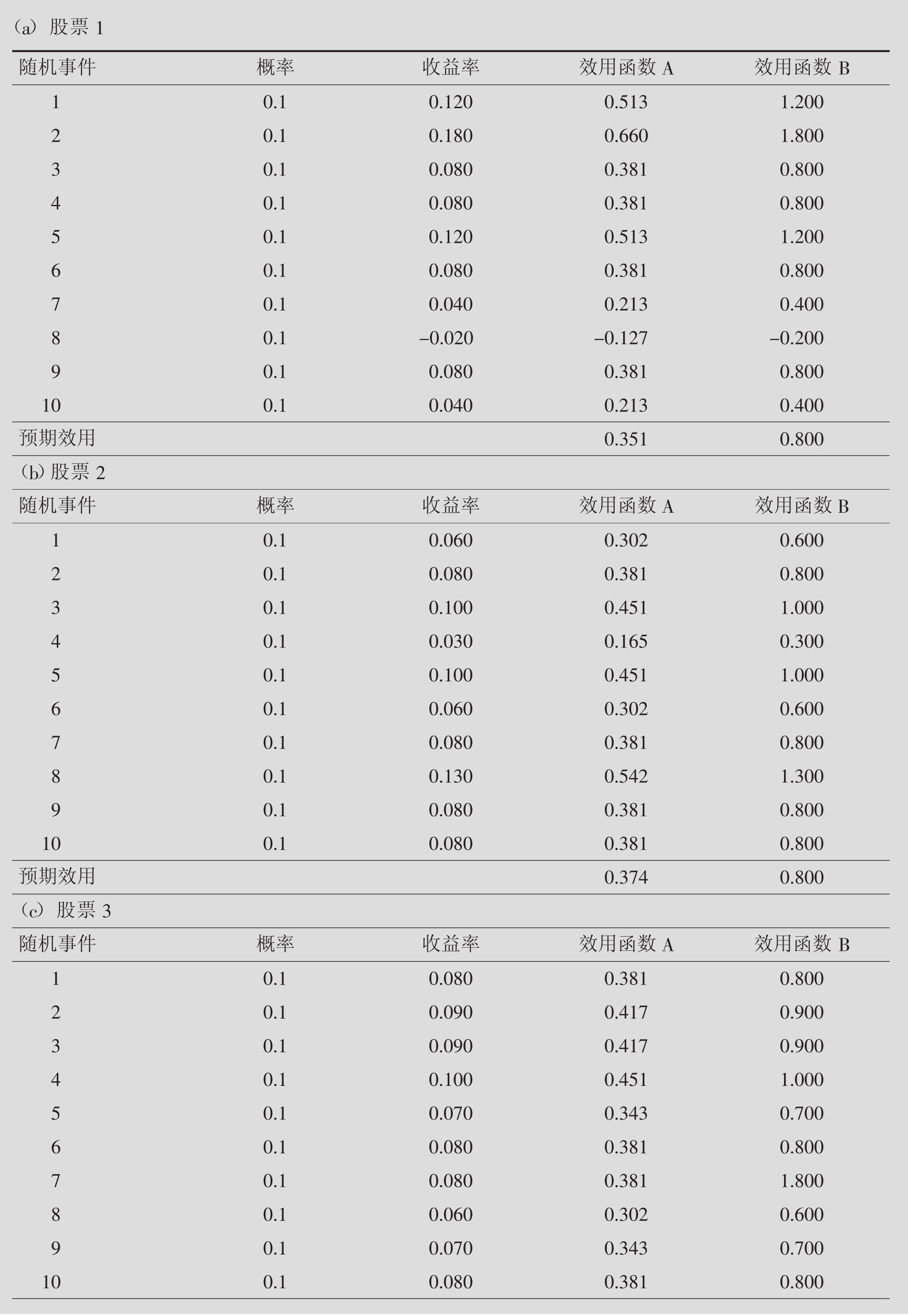
续表
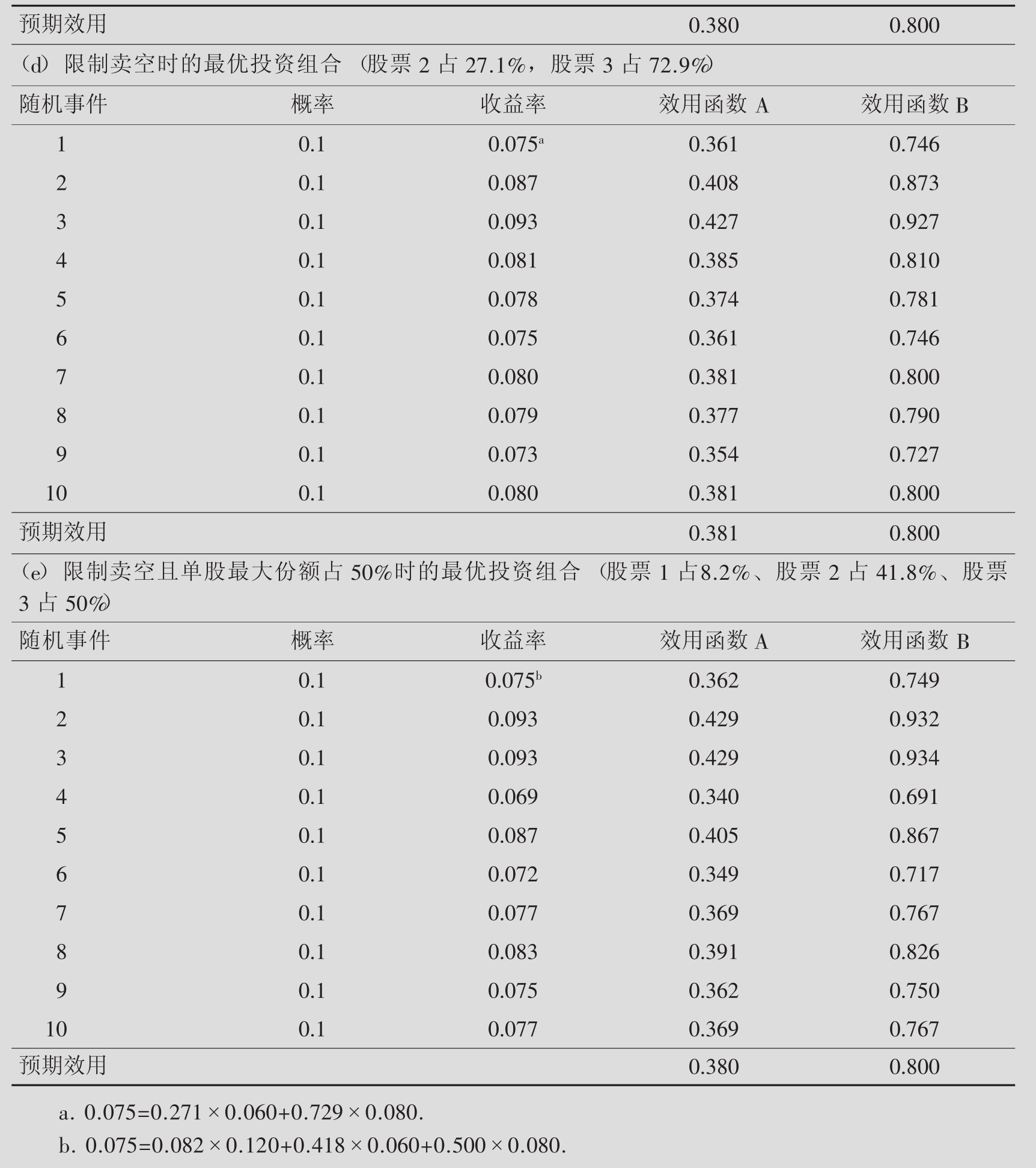
到目前为止,我们已经比较了股票1、股票2和股票3的预期效用,并得出结论说,风险投资者相对于股票1和股票2,更加倾向于投资股票3。尽管如此,这并不是说股票3是预期效用最大化者的最佳选择。毕竟投资组合概率集除了包括单独持有股票的情况外,还包括同时持有三支股票的情况。正如7.1中已经讨论过的,概率集取决于投资者所受的投资限制。正如最终表现出来的结果那样,如果对投资者设定第一组投资限定(权重之和为100%且各权重皆为正数),那么对于一个风险规避者而言(如效用函数A所示),在最佳投资组合中应向股票2投资27.1%,再把剩下的(72.9%)资金投向股票3。[19]表7.5表明,这个最优化组合(0.381)的预期效用,的确比向股票3投入全部资产(0.380)带来的预期效用要高得多。因而,尽管股票2(0.374)的预期效用比股票3的预期效用低,股票2还是被包括在最优组合中。这样做的原因在于,如果股票3的收益水平较低的话,股票2还可以表现得相对好些。比如,在股市行情8中,股票2的收益率为13%,而股票3的收益率只有6%。因此,风险规避者可以通过向股票2投资部分资金,来降低风险进而提高预期效用。比如说在随机事件8中,最优投资组合的收益率为7.9%而不是只有6%。值得再次说明的是,对风险反应中性的投资者对所有可选投资组合间的风险差异毫无兴趣,因为这些组合的预期回报都是8%,由此而来的预期效用也都是一样的(0.800)。
表7.5(e)表示第二组限制条件下(各权重之和应为100%,且各权重的大小应介于0~ 50%之间)的结果。在这个条件下,对于风险规避者而言,他的最优组合应该是:向股票1、股票2和股票3分别投资8.2%、41.8%和50%的资金。注意在这种情况下,预期效用要比没有附加限制条件下的预期效用低(0.380对0.381)。说明了这样一条投资原则:投资限制普遍地会让投资者处境窘迫(当然这得忽略投资限制给整个社会带来的好处:这些限制阻止了非法或不道德的投资行为)。需要再次指出的是,不确定风险的投资者,对以上各个可能的投资组合都没有任何兴趣。
7.5风险规避、组合多样化以及风险酬金
在前一节中,我们看到递减的边际效用在预期效用框架中会引发风险规避行为。风险规避者,在其他条件都相同的情况下,指的就是那些不喜欢风险或离散的投资者。在两项预期收益水平相当的投资中,他们总是更倾向于向一个确定的项目投资,而非向一个不确定的项目投资。对不确定风险的投资者,会完全忽视一项投资的风险,并只根据证券的预期收益来作出投资决定。如果投资者喜欢风险或离散,他们就是所谓的风险追逐者(Risk-seekers)。
大量的证据证明:有些人是风险追逐者,至少在某些时期,同时涉及的资金数额较少时是如此。举例来说,很多博彩活动,比如说国营的彩票事业,其成本远比收入要高,但是人们却仍然会购买彩票。[20]类似的,如果不解释追逐风险行为的原因,就很难解释为什么很多人会持有多样化严重不足的投资组合。[21]毕竟,投资组合多样化会降低风险(如果该组合中的单个证券有较低的依存度的话),同时,降低风险会提升风险规避者的预期效用水平(在其他条件相等时,也同样如此)。同样,也很难理解个人投资者的过量交易行为(这会导致更多与附加风险调整收入不协调的交易成本)。[22]
尽管如此,风险规避仍旧是标准假设,其原因如下:第一,有很多原因(除风险追逐外)可以解释赌博、多样化不足和过度交易,这些解释包括判断失误和第12章中讨论的错误投资偏好错误。第二,很多(机构)投资者在寻求多样化其投资组合的同时,也运用一些风险管理手段(比如说衍生金融工具)来降低投资风险。同样,在过去的20年中,向共同基金投资的家庭数量以及共同基金的数量都有了明显的增加。这个增加可以假定为是由追求低成本多样化带来的。第三,有风险的证券类别(比如说股票和垃圾债券),从历史上看,其收益水平都包括有相当的风险酬金,而这个风险酬金高于无风险债券(如T券)带来的平均收益(相关论述参见第6章)。这又是另一个金融市场中风险规避者占主导地位的表征。
证券定价理论试图解释不同证券的风险酬金水平以及风险酬金随时间推移而变化的情况。第10章和第11章将会讨论两个基本的定价理论:资本资产定价理论(CAPM)和套利定价理论(APT)。这些理论都能运用到本章所讲的一个重要观点。具体说来,为了评估证券的风险,除了要知道单独持有证券的风险以外,还应该考虑这支证券与投资者投资组合中其他单个证券间的相互依存关系。总的说来,这个证券与其他包括在投资组合中的证券依存度越高,此证券就越有可能使该投资组合的风险提高,对投资者也就越没有吸引力。因此,投资者就会对与其他证券同步变化程度强的证券要求有更高的风险酬金,而对于依存度低或者是有负依存度的单个证券要求较低的风险酬金。
如上所述,历史文献表明,有风险的证券会带来比无风险证券收益率更高的酬金比率。在这个方面,证券定价理论从定性上来说是正确的。尽管如此,大量的风险酬金依然难以理解。比如说,“链接7.2”就讨论了所谓的股本溢价难题(Equity Premium Puzzle)。
股本溢价(Equity Premium)是股票与中期国库债券预期收益之间的差额(有时也用中期国库债券充当这个比较的标准)。这个数字对投资组合配置的决定以及评估资本成本有着重要的意义。同样,它也是“应不应该向股市投资社会救济保障基金”这场争论中的核心问题。有足够的证据可以支持,在一个多世纪里,股票的收益比国库券带来的要高很多。美国股市的年均真实收益率(即排除了通货膨胀因素之后的收益率),在过去的110年中大约是一直7.9%。在同一时期内,国库券带来的收益率仅为1%不到。股本溢价——也就是此二者间的差额——是6.9%。这个差额在第二次世界大战之后甚至更大,那个时期几乎达到了8%。更进一步地说,持有有价证券带来的这种多出的收益并非为美国资本市场所独有。其他国家的有价证券收益也呈现出相同的历史规律。比如说,英国第二次世界大战后是股本溢率4.6%,同样也有著作表明,类似的差别在法国、德国、意大利以及西班牙也存在。[23]
股本溢价的规模表明,风险规避是市场中占主导地位的投资偏好。如果所有的投资者不是不确定风险,就是追求风险,就不会有大于零的风险酬金了。我们可以假设股票风险和投资者的风险规避是风险酬金的产生原因。尽管如此,历史上风险酬金的规模似乎比这些假设能说明的规模要大得多。甚至在1929~1939年的经济大萧条中,一个能较好地多样化其投资组合的投资者,如果保持把股票股息重新投资到股市,那么他/她的股票投资组合也只会下跌18%。这就暗示了,对于一个充分多样化的持股人而言,他/她就不大有可能在什么行情下遭受到灾难性的损失。如果股票的风险有限,那么就需要一个高的不合理的风险规避程度,来解释历史上大量的股本溢价。由于这个原因,其规模已经困扰了学术界和实际证券交易者们好几十年了。[24]
有人声称,现有的定价理论模型不能适当地解释投资者的风险认知和对风险的态度。[25]也有人声称历史平均收益率有被夸大的嫌疑。比如说,在计算收益率时,总是假设股票的股息会被重新投资且不用缴纳相关税费。还有人声称,历史观测的平均收益率,不能代表过去投资者对实际收益的预期(比如说,由于一些没有预见到的诸如战争之类的灾难性事件),同时它们也不能代表现在投资者对将来收益的预期(比如说,因为诸如指数化证券投资资金和ETFs这样的投资工具,使得低成本、低风险的证券投资组合甚至能为小额个人投资者所用)。这个争论很可能会在以后相当长的时期内存在。
理论联系实际7.2
FT
有价证券的中心谜题
过去三年对于那些从事证券交易的人来说,可不是什么好年头。随着全球熊市的继续,他们的“模型”显示各证券都相继一跌到底。过去16年中政府债券的表现都优于有价证券。以“道·琼斯36000点”或“道·琼斯100000点”为题的好时光已经过去多年了。
股市行情低落,而经济学家们却正努力解释为什么有价证券能产生如此高的投资收益,这可真是有点奇怪了。但是数据很清楚地表明:在长达40年的时期里,有价证券的表现都远远好于其他证券。评估的具体结果可能有出入,但是不管你选取多长的时间段,什么样的测量手段或者什么样的国家和地区,有价证券的总体收益都会大大超出无风险证券(比如说政府的国库券)带来的收益。也许由埃尔罗伊·迪姆森(Elroy Dimson)、保罗·马歇(Paul Marsh)和麦克·斯滔顿(Mike Staunton)(见其由普林斯顿大学出版社出版的《乐观的胜利》一书)提交的分析是最谨慎的了。这个分析表明在过去的一个世纪中,美国的风险酬金率为4.9%,全世界在同一时期的酬金率为4.6%。复利在很长时间内发挥的作用暗示,尽管有价证券市场在过去的3年多时间里,已经差不多缩水了一半,可计算出的股本溢价依然很高。比如,美国政府债券收益自1900年起,仍然大大高于4%。
自20世纪80年代中期以来,让经济学家们吃惊的不是有价证券会带来更高的收益——他们的理论认为,有价证券是比国库券风险更高的证券,故而投资者要求获得更高的收益——而是不能用附加风险来合理化股本溢价的规模。
拉基尼斯·梅拉(Rajnish Mehra)任职于加州大学,他是20世纪80年代初那本著作的作者之一。他最近发表了一篇论文,论述了经济学理论在“股本溢价难题”被广泛讨论以来的20年之后,是否已经能够尽如人意地解释这个问题了。因为有价证券和国债在各种不同的经济行情下表现得极为相似,他计算得出,有价证券只应比无风险证券多得1%的年酬金。他的答案是,没有一个经济学理论能充分地解释这种差异。有的学者建立的模型可以反映数据,但是他们对人类行为的假设,尤其是关于风险规避和谨慎态度的假设,“不合适的被夸大了”。这点在有价证券收益数据上就成了一个潜在的上升偏见,因为美国股市在过去的一个世纪中挺过来了;这也是一种失败,因为政府国债也会由于战争或革命带来的金融动荡而变得脆弱。在梅拉教授看来,其他解释没有触及股本溢价难题,因而也是失败的。最后他得出结论:既然经济学理论不能解释这个谜题,且长期有价证券的数据比其他任何经济学的数据系列更好,那么没有理由不认为,在下个世纪,有价证券的收益仍然会继续优于政府国债。
其他人则不同意。他们倾向于认为:既然股本溢价规模是一个彻头彻尾的谜,就没有理由期待它会继续保持高收益水平。在去年的金融分析杂志上,罗伯特·阿诺特(Robert Arnott)和皮特·伯恩斯坦(Peter Bernstein)撰文探讨了无风险国债的历史真实股市收益与投资者投资时可能预期的风险收益之间的区别(注:原文刊于由AIMR发行的金融分析杂志,2002年3~4月刊,原题为:《什么样的股本溢价才合理?》)。他们争辩道:第一,20世纪早期的有价证券投资者,从未预期过比政府债券高5%的长期酬金,仅仅是碰巧这些证券表现的比较好罢了。这样好的表现不可能在当时就被预测到。经济政策的改变,导致第二次世界大战后通货膨胀的重新出现,这就降低了国债的真实收益,却没有降低有价证券。第二,与股息相关的有价证券价值上升,尤其是80年代中期以来,这不可能在20世纪初就被预测到。第三,20世纪以后公司管理的改善,有助于有价证券收益的提升。如果证券投资者只是运气好,而不是由于附加风险得到补偿,那么就没有理由根据阿诺特和伯恩斯坦的文章,来预期将来还会有相同水平的酬金。此外,近期与有价证券相关的股息支付价格较高,这使他们相信,未来短期股本溢价“很可能接近,甚至也许会小于零”。
对有价证券投资者而言,好消息就是:如果股本溢价的“正常”水平较低,那么股息水平及其可能的上升就可以用来更好地使当前的市值正当化。但是坏消息是:21世纪有价证券不大可能表现的像20世纪那样好了。如果梅拉教授是对的,历史上高达5%的股本溢价将会在相当长的时期内得以保持,那么投资者的前景将会更加明朗。但关键是在于“在相当长的时期内”。当前,较高的股本溢价表明,美国的有价证券价值水平过高,因为只有在股价较低的时候,有价证券才可以带来比政府国债高5%的风险酬金。
资料来源:克里斯·盖尔斯:《有价证券的中心谜题》,FT.com网站,2003年3月18日。
7.6 展望:从预期效用到均值—方差分析
预期效用标准提供了一个优雅而又比较符合理论的方法来建立投资决策模型。尽管如此,寻求投资建议的个人或公司,可不会为了建议让他们预期效用最大化而心存感激。预期效用标准不是运营性的,一般而言,我们并不知道效用函数的形状,也不知道收益概率分布的形状,因而我们也就无法计算预期效用。此外,一个公司一般有几个股东,每个股东可以假设为都有不同的效用函数。结果,预期效用标准一般而言都不能应用于实践。但这个标准依然有用,因为它从理论上正确地表明了投资者的目的、预期以及限制之间的关系。同时,很多运营性的投资工具都要遵循预期效用框架中的原则。
第8章将讨论均值—方差分析,它可以看做是一个接近预期效用分析的理论框架。在均值—方差分析的框架中,投资者在预期回报或者说均值,以及以方差和标准差(方差的平方根)计量的风险,二者之间进行替换。这就在很大程度上简化了对投资者偏好以及证券概率分布的评估。在对效用函数和概率分布作出某些假定的前提下,均值—方差分析是一个很好的与预期效用分析近似的理论框架。在更加宽泛的假设前提下,它是一个有用的近似理论。与预期效用分析不同,均值—方差分析是运营性的,有较强的可操作性。实际上它是当前最流行的投资决策模型,被广泛地应用于投资组合选择申请、表现评估和风险管理等诸多方面。此外,均值—方差分析构成了多个证券定价模型的基础,比如说资本性资产评估模型(资本资产定价模型,其详细讨论参见第10章)。同时,我们强调它是预期效用理论框架的近似体,且也试图捕捉描述本章讨论的投资者目的、预期和限制三者之间的理论联系。要了解均值—方差分析的局限,发现更多均值—方差分析以外的可操作模型,就要求掌握预期效用框架的相关知识。[26]
总结
解释以下基本概念:投资组合概率组、收益概率分布和效用函数
金融经济学家一般把投资模型转化为一个在不确定的情况下,有限制的最优化的问题。三个重要的基本概念被用来补充这个宽泛的研究方法:以效用函数来描述投资者的目标,以概率分布来描述投资者对未来收益的主观期望以及这些收益实现的概率,用一个投资组合集来描述投资者面对的概率和限制。
解释投资组合选择中的预期效用标准最大值
预期效用标准说的是,一个投资者是通过解决以下有限制的最优化问题,来选择他/她的投资组合的。
![]()
上公式要受到关于权重w1,…,wn的所有投资限制。投资者各有不同,表现在以下几个方面:
■他们有不同的目标或效用函数u(R),一些人比另外一些人更讨厌风险。
■他们对未来收益分布的期望不同,此处以概率P1,…,Pm来表示。
■他们面对不同的权重w1,…,wn的限制。投资者可能受到的限制包括,比如说,卖空限制,与标准指数或长期债券分配间差异度的限制,向单个股票、经济领域、国家和证券类型投资的最大额的限制,或者还有来自社会和环境的屏障,等等。
解释什么是风险规避者
一个风险规避者,在其他条件相当的情况下,厌恶不稳定性。只要两项投资产生的预期回报是一样的,风险规避者总是更倾向于向那个确定的项目投资,而不是那个不确定的项目。在预期效用框架中,递减的边际效用产生出风险规避行为。投资者首先要通过购买最重要的商品和服务(比如说,住房、食品和衣物),来满足最基本的需要。每一附加的美元带来的效用都会更少,因为它是花在不那么重要的商品和服务上的。因此,亏损带来的痛苦,超过了赚得相当数额的收益带来的快乐。于是,投资者在其他条件相当的情况下,更倾向于投资一项确定的项目,而非不确定的。
解释为什么风险规避者一般都会多样化其投资组合,以及他/她要求获得比无风险证券收益率高的股本溢价
一个风险规避者会选择多个不同的证券以多样化其投资组合,因为投资组合多样化可以降低投资组合的风险,只要其中的证券之间没有很强的相关性。投资者的风险规避行为同样会带来比无风险证券收益率高的股本溢价。股本溢价是由于投资者冒险购买风险高的证券而获得的附加平均收益。之所以需要有股本溢价,是因为如果风险债券与无风险债券预期收益水平相同的话,风险规避者就会选择无风险债券而非风险债券进行投资。
解释为什么预期效用标准不是操作性的,同时解释为什么这个标准还是有用的
我们一般都不能在实践中应用预期效用标准,因为无法知道效用函数图像和概率分布的确切形状。然而这个理论框架依然捕捉到了投资的基本原则(投资组合概率集、收益分布以及效用函数)。许多投资工具,比如均值—方差分析框架,都要遵从预期效用框架中的原则。
关键词
套利201
不确定情况下有限制的最
优化组合196
限制性条件196
连续分布207
积累分布函数209
离散分布207
股本溢价218
股本溢价难题218
预期收益值202
边际效用211
均值202
平均收益值202
均值—方差分析208
多变量概率分布201
客观概率201
最优化196
总体相关206
总体相关度系数207
总体协方差206
总体均值202
总体标准差206
总体方差202
投资组合概率集197
投资组合权重197
风险规避215
概率密度函数207
概率分布197
风险201
无风险证券200
无风险利率200
风险追逐者217
标准正态分布208
主观概率201
不确定性196
不确定风险216
单变量概率分布201
效用函数196
方差202
练习题
1.经济学家常常借用以下三个概念来模型化投资者行为:效用函数、概率分析和投资组合概率集。
a.效用函数描述了投资者目标,给出效用函数的三大特征。
b.概率分布的目标是什么?
c.对投资组合概率集的限制有何影响?
2.假设一个投资者的效用函数是u(R)=E(RP)0.5。其中E(RP)表示投资组合P的预期收益。该投资者希望由图7.2(a)中所示的那3只股票组成一个投资组合,并进行投资。他/她是否会倾向于不持有股票1,而只持有股票2和股票3,并且让股票2的权重达到1/4,股票3的权重达到3/4?
3.假设一个投资者有这样一个效用函数对数:u(RP)=expRp投资者最开始持有1000欧元的资金,投资后盈利10%的概率为25%,而亏损5%的概率为75%。
a.风险规避者会接受这样的投资概率吗?
b.假如投资者不是盈利10%就是亏损5%的投资额,那么投资者选择冒险而不是放弃投资的概率有多大?
4.尽管证券酬金的规模表明风险规避是市场中处于主导地位的投资行为(也就是说,如果所有的投资者不是对风险反应中性就是追逐风险,那么就不可能有正的股本溢价了),历史上证券酬金的规模,似乎比能用“关于股票风险和投资者风险规避行为的假设”来说明的股本溢价规模大。经济学者和从业者已经给出了很多解释来说明历史上的股本溢价规模为什么会那么大,试着给出几条这样的解释。
5.尽管预期效用标准不是运营性的,这个标准仍然是有用的,解释为什么会这样。
若想获得练习题的参考答案,请访问Levy-Post投资网站,网址为:http://www.booksites.net/levy
参考文献
Arrow,K.J.,1951,‘Alternative Approaches to the Theory of Choice in Risk-Taking Situations’,Econometrica,19(4),404-437.
Arrow,K.J.,1964,‘The Role of Securities in the Optimal Allocation of Risk-Bearing’,Review of Economic Studies,31(1),91-96.
Barber,B.M.and T.Odean,2000,‘Trading is Hazardous to Your Wealth:The Common Stock Investment Performance of Individual Investors’,Journal of Finance,55,773-806.
Bazaraa,M.S.,H.D.Sherali and C.M.Shetty,1993,Nonlinear Programming Theory and Algorithms,2nd edn,New York:John Wiley&Sons.
Benartzi,S.and R.H.Thaler,1995,‘Myopic Loss Aversion and the Equity Premium Puzzle’,Quarterly Journal of Economics,110,73-92.
Bernouilli,D.,1738(trans.L.Sommer,1954),‘Specimen Theoriae Novae de Mensura Sortis’(Exposition of a New Theory on the Measurement of Risk),Econometrica,21(1),23-36.
Blume,M.E.and I.Friend,1975,‘The Asset Structure of Individual Portfolios and some Implications for Utility Functions’,Journal of Finance,30,585-603.
Cramer,G.,1728,Letter to Nicolas Bernouilli;extracts printed in Bernouilli(1738)and in Sommer’s(1954)translation.
Fama,E.and K.French,2001,‘The Equity Premium’,working paper 522,Chicago: University of Chicago,http://bwww.uchicago.edu/fac/finance/papers/newequity.pdf.
Friedman,M.and L.J.Savage,1948,‘The Utility Analysis of Choices Involving Risk’, Journal of Political Economy,56,279-304.
Good,R.W.,1994,‘Yes,Virginia,there is a Risk Premium,But...’,Financial Analysts Journal,50(1),11-12.
Hadar,J.and W.R.Russell,1969,‘Rules for Ordering Uncertain Prospects’,American Economic Review,59,25-34.
Hanoch,G.and H.Levy,1969,‘The Efficiency Analysis of Choices Involving Risk’, Review of Economic Studies,36,335-346.
Hartley,R.and L.Farrell,2002,‘Can Expected Utility Theory Explain Gambling?’, American Economic Review,92,613-624.
Hirshleifer,J.H.,1958,‘On the Theory of Optimal Investment Decision’,Journal of Political Economy,66,329-352.
Ibbotson Associates,2001,Stocks,Bonds,Bills and Inflation:2000 Yearbook,Chicago: Ibbotson Associates.
Knight,F.H.,1921,Risk,Uncertainty and Profit,Boston,MA:Houghton Mifflin.
Kocherlakota,N.R.,1996,‘The Equity Premium:It’s Still a Puzzle’,Journal of Economic Literature,34,42-71.
Levy,H.,1992,‘Stochastic Dominance and Expected Utility:Survey and Analysis’, Management Science,38(4),555-593.
Levy,H.,1998,Stochastic Dominance,Norwell,MA:Kluwer Academic Publishers.
Levy,H.and A.Cohen,1998,‘On the Risks of Stocks in the Long Run:Revisited’, Journal of Portfolio Management,24,60-69.
Markowitz,H.M.,1952,‘The Utility of Wealth’,Journal of Political Economy,60,151-158.
Mehra,R.and E.C.Prescott,1985,‘The Equity Premium:A Puzzle’,Journal of Monetary Economics,15,145-162.
Post,G.T.,2003,‘Empirical Tests for Stochastic Dominance Efficiency’,Journal of Finance,58(5),1905-1932.
Rothschild,M.and J.E.Stiglitz,1970,‘Increasing Risk I:A Definition’,Journal of Economic Theory,2,225-243.
Sharpe,W.F.,1965,‘Risk Aversion in the Stock Market:Some Empirical Evidence’, Journal of Finance,20,416-422.
Sharpe,W.F.,1991,‘Capital Asset Prices With and Without Negative Holdings’,Journal of Finance,64,89-509.
Von Neumann,J.and O.Morgenstern,1944,Theory of Games and Economic Behavior, Princeton,NJ:Princeton University Press.
Whitmore,G.A.,1970,‘Third-Degree Stochastic Dominance’,American Economic Review,60,457-459.
附录 累积标准正态分布
续表

要查一个均值为E(R),标准差为σ的随机变量所对应的累积概率值,首先得计算出标准分Z的值,其公式如下:Z=(R-E(R))/σ。然后,在上表中的横行中寻找对应的Z分数小数点前的首位数,再在纵行中寻找对应的Z分数小数点后的第二位数。比如说,如果一个变量的Z(R)=2,且标准差为σ=4,那么与之对应的Z分数就是(6-2)/4=1,累积概率为0.8413,或者说84.13%。上表以微软公司出品的ExcelTm软件制作。
【注释】
[1]See,for example,Sharpe(1991).
[2]This distinction was first proposed by Knight(1921).
[3]This requires that the states of the world are exhaustive(all possible scenarios are covered)and exclusive(the scenarios do not‘overlap’).
[4]In practice,the number of scenarios typically is too large to apply this approach.Section 7.2.1 discusses how this problem can be circumvented by using a continuous distribution that is described by only a few shape parameters.
[5]A histogram is the graphical representation of a probability distribution.The advantage is that we can see quickly which outcomes are most likely.The probability of an outcome is represented by the height of the corresponding bar.Many return levels have a zero probability and,hence,they do not have height in the histogram.
[6]Other measures of central tendency include the mode and the median.
[7]Variance is not the only measure of risk,but it is the most widely used.Other risk measures include the range,mean absolute deviation,skewness,kurtosis,probability of loss,expected loss and semivariance.
[8]The following equalities show that these expressions are equivalent: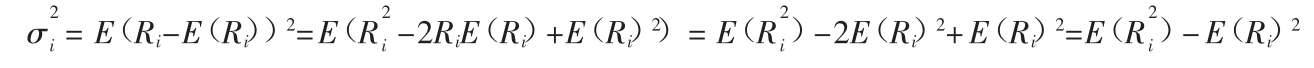
[9]The following equalities show that these expressions are equivalent:σi,s=E((Ri-E(Ri))(Rs-E(Rs)))=E(RiRs-RiE(Rs)-E(Ri)Rs+E(Ri)E(Rs))=E(RiRs)-E(Ri)E(Rs)-E(Ri)E(Rs)+E(Ri)E(Rs)=E(RiRs)-E(Ri)E(Rs)
[10]The normal distribution was first introduced by a French mathematician,Abraham de Moivre(1667-1754).Much of the appeal of the normal distribution comes form the so-called central limit theorem(CLT),which states that the sum or the mean of a large number of independent random variables is approximately normally distributed,provided the random variables obey the same probability distribution(which need not be normal).The CLT is one of the cornerstones of econometrics;it is used to derive the large-sample properties of various statistical estimators.However,despite the usefulness of the CLT,we need to be careful in applying it to real-life economic data,because real-life data frequently do not obey the assumptions underlying the CLT.For example,the return on a well-diversified portfolio of assets is a weighted average of the returns on a large number of individual assets.Still,we cannot apply the CLT and conclude that port-folio returns obey a normal distribution,because the individual assets are not independent and they do not have the same return distribution.Similarly,the portfolio return over a long period of time is a weighted average of the portfolio returns over many short time intervals.Still,we cannot apply the CLT and conclude that the portfolio returns obey a normal distribution,because the return distribution may change over time(for example,the variances and the correlations may increase during a crisis situation)and the returns may be correlated through time(for example,if asset prices do not immediately and completely adjust when new information arrives).This does not mean that portfolio returns do not obey a normal distribution;rather,it merely means that we cannot use the CLT to justify normality.The portfolio returns are still distributed normally if the indidivual assets obey a normal distribution.
[11]Formally,marginal utility is defined as the first-order derivative or u′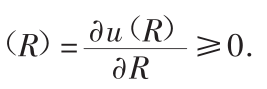
[12]In other words,the second-order derivative is negative or u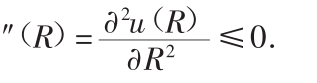
[13]Formally,utility is invariant to linear transformations;a+b×u(R)gives exactly the same ordering as u(R),for all a and b>0.
[14]The rules of differential calculus imply that the first-order derivative of u(R)=a+b×exp(c×R)is given by u′(R)= b×c×exp(c×R).In our case,we have a=1,b=-1 and c=-6.
[15]The rules of differential calculus imply that the first-order derivative of u(R)=a+b×R is given by u′(R)=b.In our case,we have a=0 and b=10.
[16]The maximisation of expected utility was first proposed as a criterion for decision-making under uncertainty by Cramer(1728)and then Bernouilli(1738).Much later,the axiomatic justification for this criterion was provided in an appendix to the classic work by Von Neumann and Morgenstern(1944).
[17]Specifically,1-exp(-6×0.12)=0.513,1-exp(-6×0.08)=0.381 and 1-exp(-6×0.04)=0.213.
[18]We use a loose definition of risk and we use the terms‘risk’and‘dispersion’interchangeably.In general,we may define a risk-averter as somebody who dislikes so-called mean-preserving spreads.A mean-preserving spread transfers weight from the centre of the density function to its tails without changing the mean.For example,consider two lotteries.The first lottery gives a 10%probability of winning$1000 and the second lottery gives a 1%probability of winning$10000.In this case,the latter lottery is a mean-preserving spread of the former.In both cases,the mean is$100.However,the second lottery has more probability mass in the tails than the first one.All investors who follow the expected utility rule and have a concave utility function will choose the first lottery,for the simple reason that the probability of winning is ten times higher, while the utility of$10000 is less than ten times higher than the utility of$1000(marginal utility is diminishing).Interestingly,the second lottery can be seen as a compound lottery where the lottery player first plays the first lottery(a 10% probability of winning$1000)and,if he or she wins the$1000,he or she then plays a follow-up lottery with a 90%probability of losing the$1000 and a 10%probability of winning an additional$9000.The follow-up lottery has a zero-mean and all risk-averters will choose to avoid it.
[19]The proof that this is the optimum is beyond the scope of this book,as it requires non-linear constrained optimisation.The interested reader is referred to Bazaraa et al.(1993).The reader who is already familiar with optimisation should note that objective function(expected utility)is concave(provided the utility function is concave)and the feasible set(the portfolio possibilities set)is convex(provided we include only linear equalities and inequalities,such as in Equations 7.2 and 7.3).Hence,the first-order optimality condition is necessary and sufficient to determine the optimum.
[20]See,for example,Friedman and Savage(1948),Markowitz(1952)and Hartley and Farrell(2002).
[21]See,for example,Blume and Friend(1975).Chapter 8 discusses underdiversification further.
[22]See,for example,Barber and Odean(2000).This study found that the average household turns over 80%of its common stock portfolio each year.The associated transaction costs,such as commissions running and a spread between the bid and ask prices,substantially reduces the average net return below the levels of a passive strategy of holding an index fund.20%of the households sported a 283%average annual turnover rate;investors in this group basically swapped out their entire portfolios three times a year.Adjusted for risk,the net return of this high-turnover group lagged the market by as many as 10.9 percentage points per year.
[23]See,for instance,Ibbotson Associates(2001).
[24]See,for instance,Mehra and Prescott(1985)and Kocherlakota(1996).
[25]See,for instance,Benartzi and Thaler(1995).
[26]If mean-variance analysis is considered too restrictive,then the framework of stochastic dominance offers an alternative. In contrast to mean-variance analysis,stochastic dominance analysis does not require a quadratic utility function or normally distributed returns.Rather,stochastic dominance analysis relies on a general set of assumptions about the preferences of the investor and the statistical distribution of asset returns.The following classic works provide the theoretical foundation for stochastic dominance analysis:Hadar and Russell(1969),Hanoch and Levy(1969),Rothschild and Stiglitz(1970)and Whitmore(1970).Since its conception,stochastic dominance analysis has seen considerable theoretical development and empirical application in various areas of economics.Useful surveys of the topic can be found in Levy(1992)and Levy(1998).Finally,an empirical methodology for applying stochastic dominance analysis to portfolio selection and portfolio evaluation is found in Post(2003).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














