均值—方差分析

第8章　均值—方差分析

投资新闻8

FT

与不确定性斗争的启发

风险年表

■1654年法国数学家布莱斯·帕斯卡（Blaise Pascal）和皮尔·德·费麦（Pierre de Fermat）对赌博游戏进行了分析，第一次正式提出了概率理论的数学基础。

■1662年英国商人约翰·格朗特（John Graunt）应用具有革新意义的样本方法公布了伦敦出生和死亡的数据，并用统计推断的方法估算出了伦敦的总人口。

■1687年爱德华·劳埃德（Edward Lloyd）在伦敦塔街开了一家咖啡馆，并在1696年列出了关于欧洲信件运输情况的清单（Lloyd’s List）。

■1696年英国数学家、天文学家埃德蒙·哈利（Edmund Halley）说明了寿命数据如何用于确定不同年龄的人寿保险价格。

■1713年瑞士数学家雅各布·贝努力（Jacob Bernoulli）的“大数定理”在其死后发表。该定理表明了，如何从有限的信息中识别概率和统计显著。

■1733年法国数学家亚伯拉罕·德·莫伊乐（Abraham de Moivre）提出了正态分布——一系列变量以其均值为中心的分布形式，并从中得出了标准差的概念。

■1738年雅各布·贝努力（Jacob Bernoulli）的外甥丹尼尔（Daniel）引入了效用概念：风险不仅决定于概率的计算，而且决定于风险承担的结果价值。

■1885年英国科学家弗朗西斯·卡顿（Francis Galton）发现了均值回归——存在恢复到均值的趋势。

■1944年美国学者约翰·冯·纽曼（John von Neumann）和奥斯卡·摩根斯坦（Oskar Morgenstern）在《博弈论与经济行为》一书中应用策略博弈的理论（而不是概率赌博游戏）在商业和投资中做出决定。

■1952年美国经济学家哈里·马科维兹（Harry Markowitz）在数学上证明了期望收益和风险是直接相关的，但是投资者可以通过分散化的投资来降低收益的方差且不改变原来的期望收益。

■1970年美国学者菲舍尔·布莱克（Fischer Black）和迈伦·斯科尔斯（Myron Scholes）发表了一个用于计算期权价值的数学模型。

资料来源：彼德·L.伯恩斯坦：《与不确定性斗争的启发》，《金融时报》2000年4月25日。

学习目标

在完成本章的学习后，你应能够：

1.归纳均值—方差标准

2.解释均值—方差理论的经济意义

3.讨论计算均值—方差的两种方法

4.区分有效和无效投资战略

在投资新闻8中给出了对风险的理解、测量以及评价其影响的科学发展年表。第一次大突破来自布莱斯·帕斯卡和皮尔·德·费麦，他们运用数学工具分析简单的赌博游戏，并创建了概率论基础。这一章将主要介绍由诺贝尔奖得主哈里·马科维兹开创的均值—方差理论。

在第7章中，我们介绍了金融学家如何把投资决策转化为不确定条件下的有约束最优化问题。期望效用理论（Expected Utility Framework）表明了这个问题各个部分（资产组合可行集，资产收益的概率分布——描述投资者对未来的主观期望，投资者的效用函数——刻画投资者的投资目标）之间的理论关系。正如上一章所说，一般我们不能在实际中应用期望效用理论，因为我们并不知道效用函数的具体形状和具体的概率分布。均值—方差理论（Mean-variance Framework）则是期望效用理论的一个很好的近似，它是目前分析投资决策最常使用的模型。该理论已经被广泛应用于资产组合选择、业绩评估以及风险管理，并帮助投资者选择优化的分散（均值—方差）组合。

简单地概括一下均值—方差分析的主要思想将有利于读者理解。在均值—方差理论中，效用函数和收益分布将由两个参数（期望收益或投资组合的平均收益；方差或标准差——方差的平方根）来描述，投资可能性由均值—方差可行集代表。在给定个人投资收益分布和投资者面临的投资限制情况下，它给出了可行的资产组合的均值—方差集。而且，均值—方差无差异曲线还刻画了投资者在风险与收益之间的替代选择关系，它是在同一期望效用水平下所有均值与方差的组合。正如在期望效用理论中一样，我们并不知道均值—方差无差异曲线的具体形状，但是知道投资者是风险规避的，即他们偏好更多的收益（见第7章）。所以，无论个人的无差异曲线如何，每个投资者都会偏好高均值和低方差。这使得我们能够建立均值—方差有效标准——如果不存在一个可以获得更高均值和更低方差的资产或资产组合，那均值—方差就是有效的。运用这一准则，我们可以得到一个有效的均值—方差边界，它是均值—方差可行集中包括有效资产组合的部分。无论投资者的无差异曲线形状如何，他们都会从有效边界上选择投资组合。该理论使投资者不用考虑所有可行的投资组合，而仅仅需要考虑有效的资产组合即可，从而大大地简化了投资问题。

这一章的结构安排如下：8.1节介绍均值—方差分析与一般期望效用理论（第7章讨论的）之间的关系，并详细解释了均值—方差无差异曲线和均值—方差标准。8.2节转入投资组合均值和方差的计算。投资组合的均值能够简单地通过对组合中单个资产均值的加权平均来计算，但计算其方差则要复杂得多，还必须考虑单个资产之间的依赖程度。最后，8.3节将讨论均值—方差资产组合可行集和均值—方差有效边界。

8.1　均值—方差分析的基本原理

在均值—方差理论中，投资者仅关心他们投资组合的均值和方差。均值—方差投资者的期望效用能表示为均值和方差的函数。由于假设投资者偏好高收益和低风险（见第7章），那么期望效用就是均值的增函数、方差的减函数。于是第一个问题自然是，我们能否使均值—方差分析与一般期望效用理论相联系呢？基本上有两个维护均值—方差分析的理由：

■收益分布可以近似看成是正态分布（Normal Distribution）。^[1]

■效用函数能由二次函数（Quadratic Function）来近似。

8.1.1　正态的收益分布

正如第7章所述，如果资产的收益服从正态概率分布（Normal Probability Distribution），那么资产组合的分布仅用均值和方差就可以刻画，但是在现实中正态分布的假设是非常苛刻的。^[2]例如，在大多数收益序列中存在肥尾问题，即在给定均值和标准差（Standard Deviation）的情况下，出现极高或者极低收益的概率比根据正态分布得出的概率要大很多。也就是说，分布的“尾巴”比正态分布时要“肥”。^[3]例如，在1994年11月19日的那一周内，墨西哥比索贬值了40%。假设一个正态分布，并给定比索的历史均值和方差，我们将能够预测比索在整个存在时期内的数量变动。但即使是在相对较短的时期内——过去20年，一些所谓的“万分之一概率事件”已经发生：1987年美国股市的崩盘；1992年欧洲汇率机制（ERM）的失败；1996年铜价骤跌；1994年比索贬值；1997年泰铢、菲律宾比索和马来西亚元的贬值以及2001年土耳其里拉的贬值，等等。其中一个可能的解释是，在这段时期内资产的收益呈现出正的相关性：如果一个负的收益可能伴随着另一个负的收益，那么出现一个更大的负收益的概率要比它们之间不相关时要高得多。^[4]另一个解释是，在该时期内资产收益的方差实质上是变动的，如果我们忽视这些变动而假设方差不变，那么极端的收益将会比预期发生得更频繁。^[5]

在大多数资产收益序列中，另一个使之不断偏离正态性的原因是收益的不对称。许多资产具有“正的偏度”，即高收益的发生概率要高于同样损失的概率。^[6]具有较高增长潜力的公司股票、可转换债券和多头期权都是具有较高正偏度的例子。相反，负偏度是指高收益的概率低于同样损失具有的概率。例如，买权的卖者将面临巨大的损失风险和有限的收益（可参见第19章）。即使投资组合中的单个资产都是正偏度，一个较好的分散投资组合仍然能有很高的负偏度（这是一个悖论，因为投资者通过分散投资可以规避遭到巨大损失的风险或负偏度）。一个合理的解释是，在危机时期，相关性将趋于增加，当需要分散化的时候这种相关性却减少了分散的效力。这意味着很大的负收益将比巨大的正收益更频繁的出现。例如，图8.1对从1939年12月～2003年11月S&P 500的月收益历史分布与具有同样均值和方差的正态分布作了对比，^[7]很明显可以看出，实际分布的左尾“太肥”，且较高负收益率发生的频率比根据正态分布得出的要大很多。

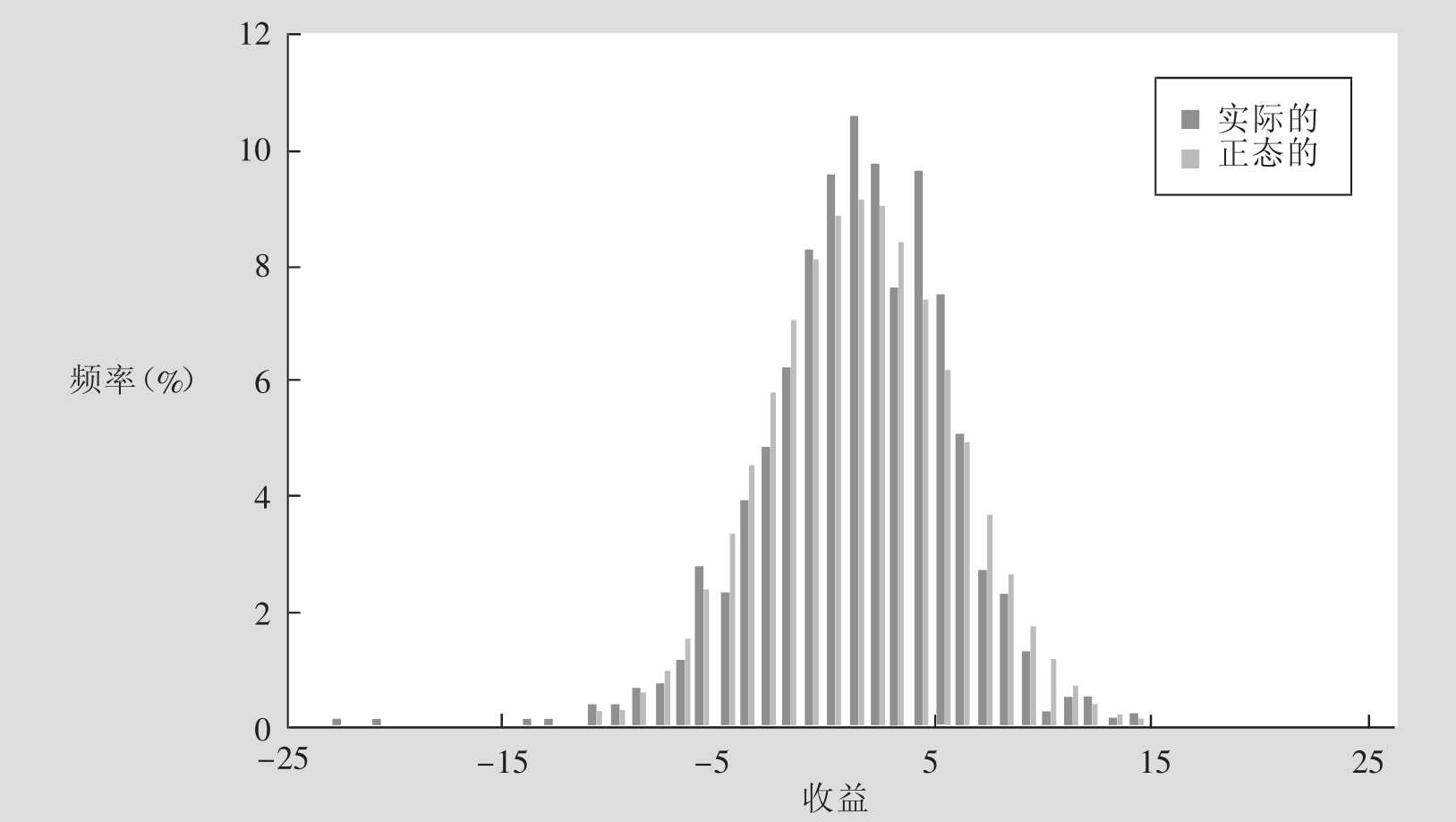
图8.1　S&P 500指数的月度收益率柱状图（1939年2月～2003年10月）

出于以上原因，正态分布一般并不能完全刻画资产和资产组合的风险和收益。

8.1.2　二次效用函数

如果投资者的效用函数是“平滑的”（即不存在任何“扭结”或边际效用不存在“跳跃”）和凹状的（边际效用递减），那么在典型的投资收益范围内，我们可以用二次效用函数（Quadratic Utility Function）来近似代替投资者的效用函数。^[8]二次效用函数采用如下的形式：u（R）=a+bR+cR²，其中a，b>0和c<0，a、b、c共同决定效用函数的形状。^[9]对这一效用函数形式，其期望效用为：^[10]

它仅仅是均值和方差的函数。另外，期望效用随着均值的增大而增大，随着方差的增大而减小。^[11]为了说明这一性质，图8.2给出了一个效用函数，它是图7.4中的负指数效用函数u_A（R）=1-exp（-6R）的近似。^[12]很明显二次函数在一个相对范围内给出了一个很好的近似（在图7.2中，-2%是最小值，18%是最大值），所以在这种情况下，我们可以踏实地假设投资者仅关注均值和方差。对比图7.2和表7.5，我们可以看到均值和方差标准与期望效用标准具有精确的一致性。一个资产或组合的方差越低，其期望效用就越高。值得注意的是，当图7.2（b）中的概率分布不满足正态假设时，这一性质仍然成立。

该图显示了负指数效用函数u_A（R）=1-exp（-6R）和二次效用函数u_C（R）=1+4R-8R²。

在许多情况下，这些条件（收益率分布近似呈正态或投资者效用函数近似为二次函数）中至少有一个能近似满足，所以均值—方差分析是一般期望效用理论的一个很好近似。^[13]

图8.2　一个效用中数的二次近似

8.1.3　均值—方差无差异曲线

在均值—方差理论中，投资者仅需要关注其投资组合的均值和方差，而且他们将偏好更大的均值和较小的方差。这使得投资问题得到大大的简化。接下来我们要做的是，如何具体化投资者在均值和方差之间的主观替代关系。胆小的投资者具有更高程度的风险规避，他们只有在期望收益率很高时才会接受一定的风险，而更具冒险精神的投资者则有较低的风险规避，他们只需要较小的风险补偿就愿意接受较大的方差。均值—方差无差异曲线（Mean-variance Indifference Curves）是表示投资者在风险和收益之间主观替代关系的有用工具。

图8.3说明了无差异曲线的概念。假设一个投资者持有资产A，该资产的期望收益率是E（R_A），标准差为σ_A，那么投资者在资产A与A₁间作交换是否明智呢？我们可以肯定，相对于资产A投资者将不会选择A₁，因为资产A₁与A具有同样的期望收益，但却具有更高的风险（σ_A1＞σ_A）。由于投资者喜欢高收益和低风险，所以资产A₁比A代表更高的效用水平。现在让我们来对比一下资产A与A₂，看看投资者是否愿意用资产A来交换A₂？回答是肯定的，因为资产A₂提供了更高的期望收益E（R_A2）＞E（R_A），而风险却与A相同。所以，资产A优于A₁，资产A₂优于A。在图8.3中，如果我们沿着曲线从资产A₁移动到A₂，那么表示该投资者从一个劣于A的资产移动到一个优于A的资产。但在沿这一路径移动时，经过一点A₃，其中资产A₃与A对于投资者而言是无差异的。同样可以得出B₂资产优于A，而资产B₁劣于A，所以必存在一点B₃，使得它与A是无差异的。我们可以对那些接近或者远离A的点重复上述操作，那将得到一条包括所有无差异点的曲线，如，A与A₃。由于投资者认为该曲线上的每一点在风险和收益上都是等价的，并认为在曲线上任两点之间交换是无差异的，所以称曲线I为无差异曲线（Indifference Curve）。在无差异曲线上任何投资点都代表了同样的期望效用水平。沿着这条曲线移动，投资者要么获得高风险、高收益；要么获得低风险、低收益。在同一无差异曲线上无论怎样移动，投资者对这些资产都具有同样的偏好。

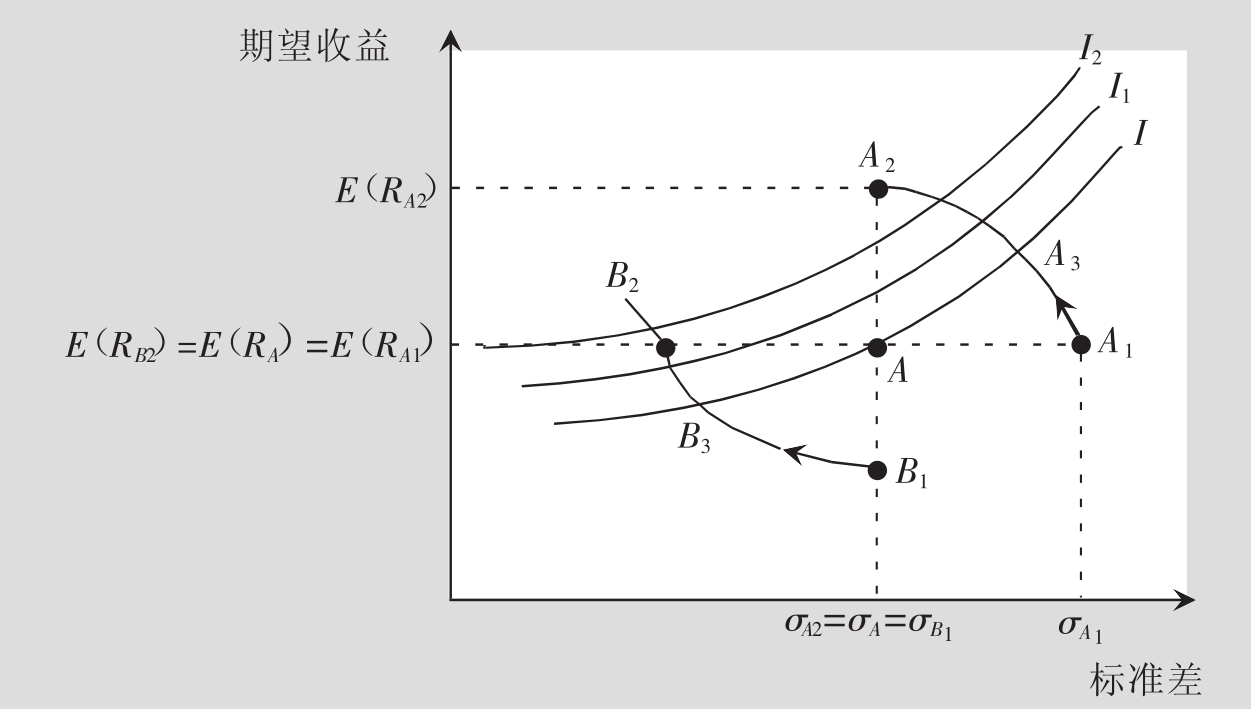
图8.3　无差异曲线

资料来源:利维：《投资学入门》第二版。

如果以垂直于A的点开始重复上述操作，就可以得到另一条高于I的无差异曲线。无差异曲线越高，则代表了越高的期望效用水平，投资者将更偏好它，因为他们在给定的风险水平下能够得到更高的期望受益。同样，无差异曲线I₂代表的期望效用水平比I₁高。

无差异曲线的基本特征如下：

■在一条给定的无差异曲线上的所有点对投资者来说都具有同样的期望效用水平。

■投资者偏好高均值和低方差，所以无差异曲线是向右上方倾斜的。如果我们增加方差，就必须也增加均值以获得同样的期望效用。曲线的斜率反映了风险和方差之间的替代关系，或者说表示了承担额外一单位的风险所要求的风险补偿。

■无差异曲线是凸的，即它是向期望收益的坐标轴弯曲的。也就是说，用于补偿额外单位风险的期望收益是递增的。即使风险补偿很低，大多数的投资者仍准备接受一定的风险，但是即使在风险补偿很大时，也没有投资者愿意接受非常巨大的风险。^[14]

■移动到更高的无差异曲线（如从曲线I移动到I₁，或者从I₁移动到I₂），将增加投资者的期望效用。所以试图达到最高可能的无差异曲线就等于获得最高可能的期望效用。

■像效用函数一样，无差异曲线也是主观的，它们在不同的投资者之间具有不同的形状。对于一个给定的投资者，在不同的时间，其形状也可能不一样。

8.1.4均值—方差的有效性

正如在期望效用理论中一样，我们一般不知道无差异曲线的具体性状（代表投资者的目标）。要改进投资工具，以适用于所有的投资者，而不是仅仅适用于具有特殊效用函数的特殊投资者。幸运的是，我们知道一些适用于所有投资者的一般性质：偏好更高的收益，厌恶较低收益，且规避风险（无差异曲线向右上倾斜）。也就是说，投资者①在同样（或更高）期望收益情况下偏好最低方差；②在同样（或更低）方差下偏好最大的期望收益。这使得我们能够扩展均值—方差效率标准（Mean-variance efficiency Criterion），如果以下两个条件的其中之一得到满足，则称投资A优于投资B：

E（R_A）≥E（R_B），σ²_A＜σ²_B

或者

E（R_A）＞E（R_B），σ²_A≤σ²_B

如果投资A优于B，则所有风险规避的投资者相对于B而言将会更偏好A。一个投资不劣于所有其他的投资，则称之为均值—方差有效（Mean-variance-efficient）。对于任何有效投资，我们可以得到一个风险规避者的最优投资（该投资使得投资者处在最高的无差异曲线上，或它最大化了投资者的期望效用）。相反，一个无效的投资被定义为至少有一个其他的投资优于它，它对于风险规避者来说不是最优的。

表8.4列出了图8.3中的7个资产之间的占优关系和有效性分类。从表中可以看出，只有资产A₂和B₂是有效的，这两个资产都不被其他任何资产占优。而另外的5个资产都是无效的，因为存在至少一个资产比它具有更高的均值和更低的方差。

表8.4　均值—方差占优关系和有效分类

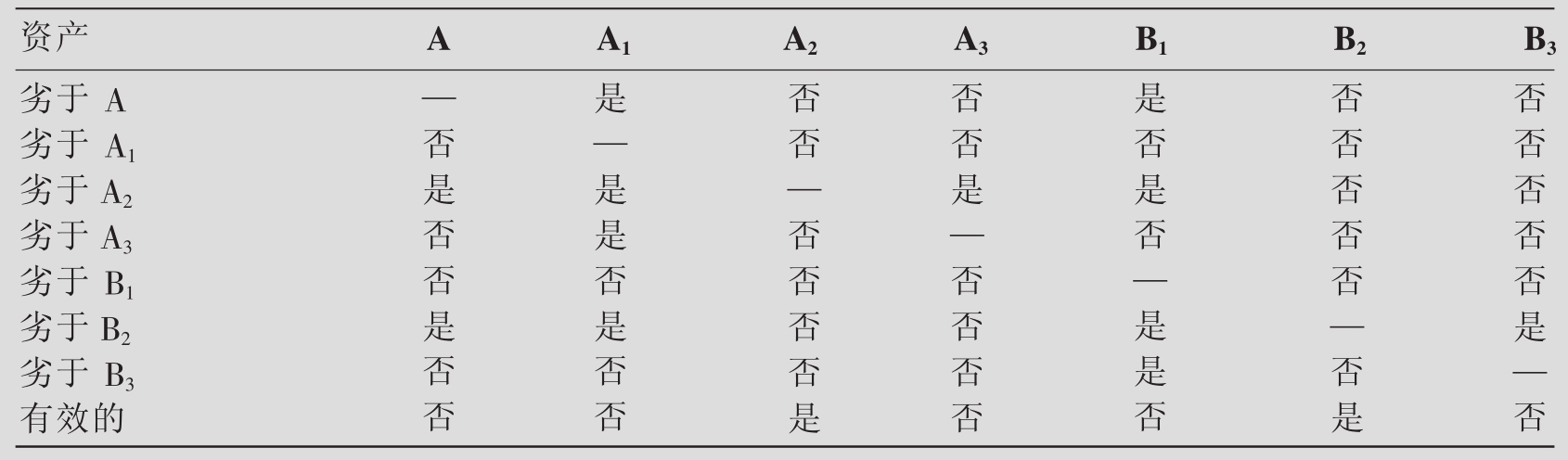
必须注意，均值—方差效率标准仅能给出各种选择之间的局部排序，而不能获得对所有投资选择的等级评定，且不能够判断出“最好的”（或“最坏的”）的投资。而且效率标准只能够区分有效资产（不被所有其他资产占优的资产）和无效资产（至少被其他一个资产所占优的资产）。该标准的长处是：能够应用于所有的风险规避者；而短处是：一般不能够得出最优的投资。为了能够从有效资产中选出最优的，还需要关于投资和偏好的更多信息（投资者在均值和方差之间的主观替代关系）。

8.2　资产组合的均值和方差

通过以上的分析，我们已经知道了均值—方差标准是如何起作用的，以及它的经济意义，下面将解决资产组合的均值和方差的计算问题。有两种方法：直接法和间接法。从概念上看，直接法是最简单的，但是它要求必须知道各种可能情况下所有单个资产的全部信息；而间接法仅需要知道单个资产收益的均值和单个资产之间的协方差，所以它能够避免直接法面临的困难。从上述讨论可知，用间接法计算资产组合均值比较简单，我们仅需要计算单个资产均值的加权平均即可，但是用间接法计算组合方差就比较麻烦了。并不能仅仅通过计算单个资产方差（Variances）的加权平均来得到组合方差，还必须考虑组合中单个资产之间的依赖关系，这需要用协方差（Covariances）或相关系数来度量。尽管计算有些复杂，但其要求的信息不多（不需要单个资产收益的各种具体观测值），而且间接法能使我们对资产组合方差的决定因素以及分散投资有效性有更深入的理解。

8.2.1计算资产组合均值和方差的方法

计算资产组合均值和方差最简单的方法是，对每一个可能的状态计算资产组合收益，即个人资产收益的加权平均

其中，w_i是组合中资产的权重；R_i,j是j状态下i资产的收益。根据方程7.4和方程7.5（见第7章）能够得到资产组合均值（Portfolio Mean）和资产组合方差（Portfolio Variance）：

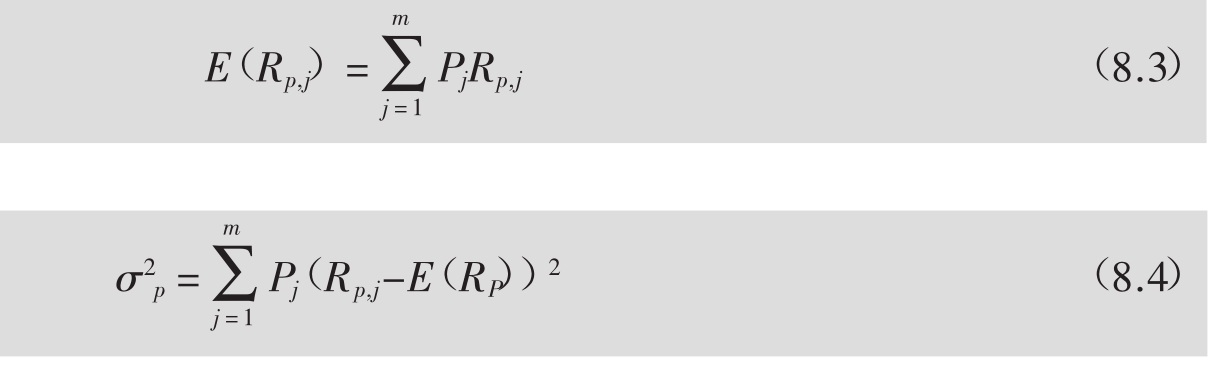
这一方法就是计算资产组合均值和方差的直接法（Direct Approach）。在这一计算中，资产组合被看成和其他的单个资产类似，所要求的计算是直接的。表8.5给出了表7.5（d）中优化组合的计算。

这一组合的投资权重分别是w₁=0，w₂=0.271，w₃=0.729。

在这个例子中，仅有很少的状态（m=10），且知道相应的收益和概率，所以直接法是很简单的。但是，个人的状态以及相应的收益往往是不知道的，或者状态的数量可能非常大（对于一个连续的收益分布，状态数量是无限大的）。为了避免这一问题，我们可以采用间接法（Indirect Approach）。

8.2.2　间接方法

计算资产组合均值的间接法很简单。把8.2式代入8.3式，可以得到:

所以资产组合的均值是个人资产均值的简单加权平均。很显然，投资于w_i资产的财富比例越大，它对资产组合均值的影响就越大。在极端的情况下，当把所有的财富（100%）都投资于一种证券时，资产组合的收益率均值就等于该证券的均值。

例如，表8.5中（0.080）的资产组合均值可以由其单个资产均值的加权平均得到：

w₁E（R₁）+w₂E（R₂）+w₃E（R₃）=（0×0.080）+（0.271×0.080）+（0.729×0.080）=0.080

综上所述，资产组合的期望收益率可以用下面两种方法计算：

■首先计算所有可能的资产组合的收益（用资产组合的权重作为计算的权重），然后用状态的概率作为其权重计算所有状态的加权平均。

■先计算所有单个资产的均值（用状态的概率作为其权重），然后再用资产组合的权重作为其权重计算所有资产均值的加权平均。

用间接法计算资产组合的方差要复杂得多。原因是我们不能把单个资产方差的加权平均作为资产组合的方差，必须考虑组合中单个资产之间的依赖性。但是由于它并不要求单个资产收益的观测值，所以间接法仍然非常有用，并且它还能使我们更好地理解资产组合方差的决定因素和分散组合的好处。

首先，把8.2式代入8.4式，得到：

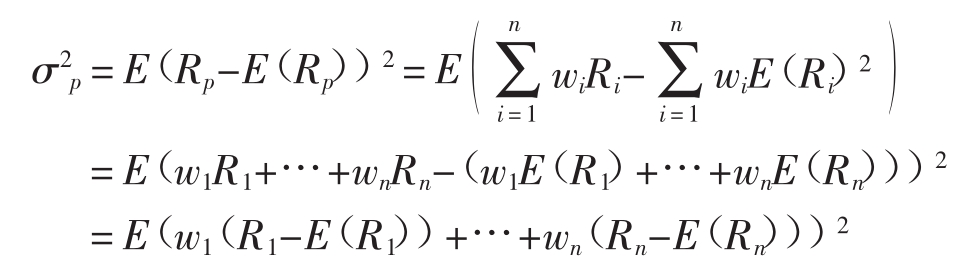
打开括号，它包括括号内任意一对因素的乘积以及每一因素与自己的乘积，即：

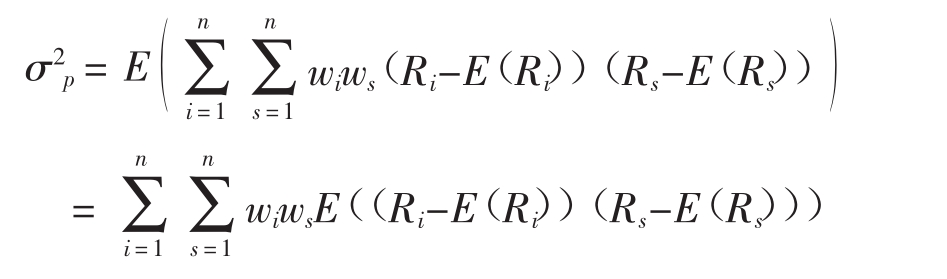
其中最后一个等式的和都是常数，而不是随机变量的事实得出，所以E（w_iw_s（R_i-E（R_i））（R_s-E（R_s）））=w_iw_sE（（R_i-E（R_i））（R_s-E（R_s）））。又由于σ²_i=E（R_i-E（R_i））²，σ_i,s=E（（R_i-E（R_i））（R_s-E（R_s））），得到：

表8.5　计算一个由27.1%股票2和72.9%股票3组成的资产组合的均值与方差的直接方法

有时资产组合的方差也写成另外一个等价形式——把方差分成两部分：

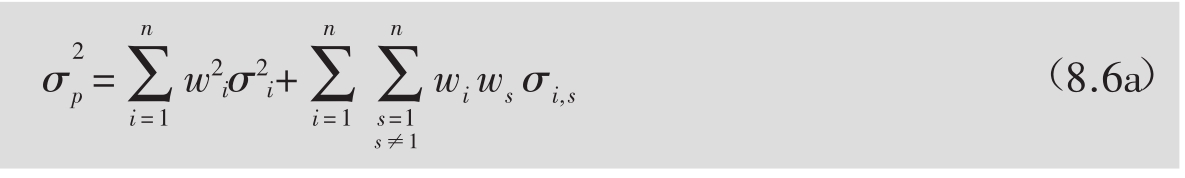
第一部分是所有单个资产方差的加权之和，第二部分是所有协方差之和。为了保证没有对方差因素重复计数，在第二部分中加上了限制条件，也就是说，对除了方差以外的所有协方差加总（注意此时的协方差就是方差）。值得注意的是，在第二部分每一个因子又出现了两次，比如w₁w₂σ_1,2和w₂w₁σ_2,1，而σ_1,2=σ_2,1，即它们是相等的。这一事实对于所有的协方差都是这样。所以方差方程也可以写成：

对方差的第二部分乘以2，表明该部分出现了两次，但在第二个求和操作中必须加上限制。比如s＞i，当i=1，s=2，有因子w₁w₂σ_1,2，加上了限制条件s＞i，我们就不用计算w₂w₁σ_2,1了，因为在因子w₁w₂σ_1,2上乘了2，已经把w₂w₁σ_2,1考虑进去了。

由于ρ_i,sσ_iσ_s=σ_i，s，在公式8.6、8.6a和8.6b中，用ρ_i,sσ_iσ_s替代σ_i，s，那么资产组合的方差的计算就不依赖协方差σ_i，s而依赖相关系数ρ_i,s了。例如，在方程8.6中，做这样的代换，可以得到：

在仅有两个单个资产（n=2）的简单情况下，考虑公式8.6、8.6a和8.6b，则有：

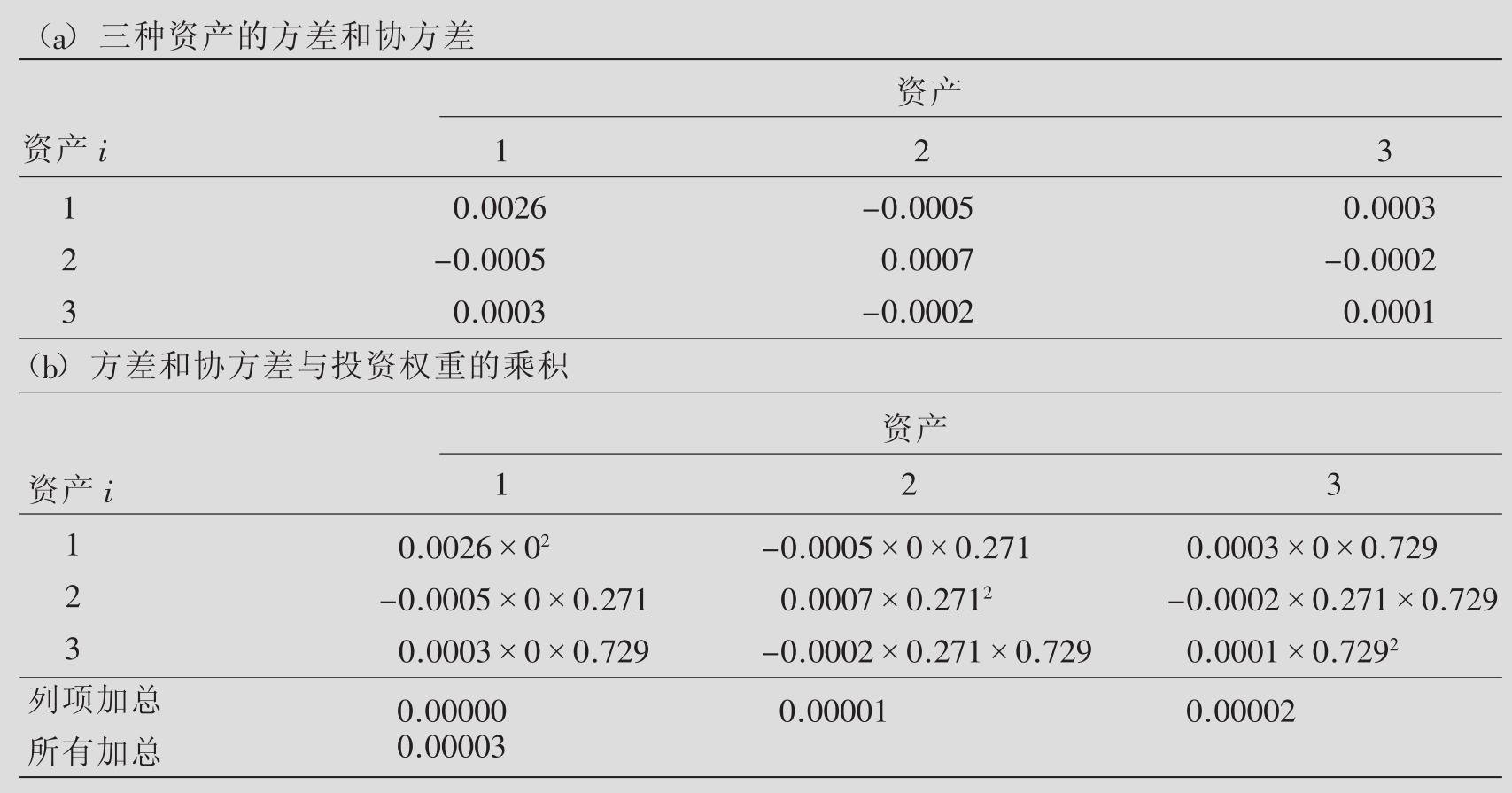
表8.6就用间接法来计算表8.2中的资产组合的方差。这一资产组合由图7.2（a）中的3只股票加权平均得到；投资的权重分别是w₁=0，w₂=0.271，w₃=0.729。表8.6（a）列出了各个资产的方差——协方差矩阵σ_i,s，数据直接来自图7.2（a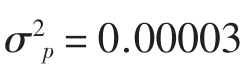）。表8.6（b）把这些因子乘以相应的权重，或者那么资产组合的方差就是这些乘积之和，即。正如预料的一样，这一结果和在表8.5中用直接法计算的一样。利用表8.6（a）的基本信息，我们可以用表8.6（b）的方式来计算具有任意权重（w_i）的资产组合的方差。

表8.6　计算一个由27.1%股票2和72.9%股票3组成的资产组合的均值与方差的直接方法

8.3　有效与无效投资战略

上一节中介绍了两种计算投资组合均值和方差的方法——直接法和间接法。下面将要介绍均值—方差概率组（Mean-variance Possibilities Set）。均值方差概率组的形状是由组合权重或者组合概率组这些限制性条件决定的（参见7.1节），限制越多，均值方差概率组越小。该组合包括所有可能的投资组合。一般地，我们不能得到单一的“最优组合”，因为不同的投资者具有不同的无差异曲线，而且无差异曲线的具体形状我们也并不知道。在8.1.4节中得到的均值—方差标准指出：投资者①面对同样（或更高）的期望收益，将会偏好最低的方差；②而面对相同（或更低）的方差时，将偏好最高的期望收益。应用这一标准，投资者将会选择那些来自均值—方差概率组子集中的投资组合。这一子集我们就称之为效用均值—方差边界（Efficient Mean-variance Frontier）。因为面对同样（或更高）的期望收益，投资者会选择最小方差，那么他们将仅关注那些在给定均值下具有最小方差的投资组合，或仅关注均值—方差边界（Mean-variance Frontier）。均值—方差边界可分成两部分：有效边界（Efficient Frontier）和无效边界（Inefficient Frontier）。有效边界是指那些在给定方差下具有最高均值的投资组合。为了更好地介绍这两个概念，本节将首先考虑仅有两个不相关的资产构成的组合，然后再扩展到由n个资产组成且它们之间相关的复杂情况。

8.3.1　两资产情况下的有效与无效边界

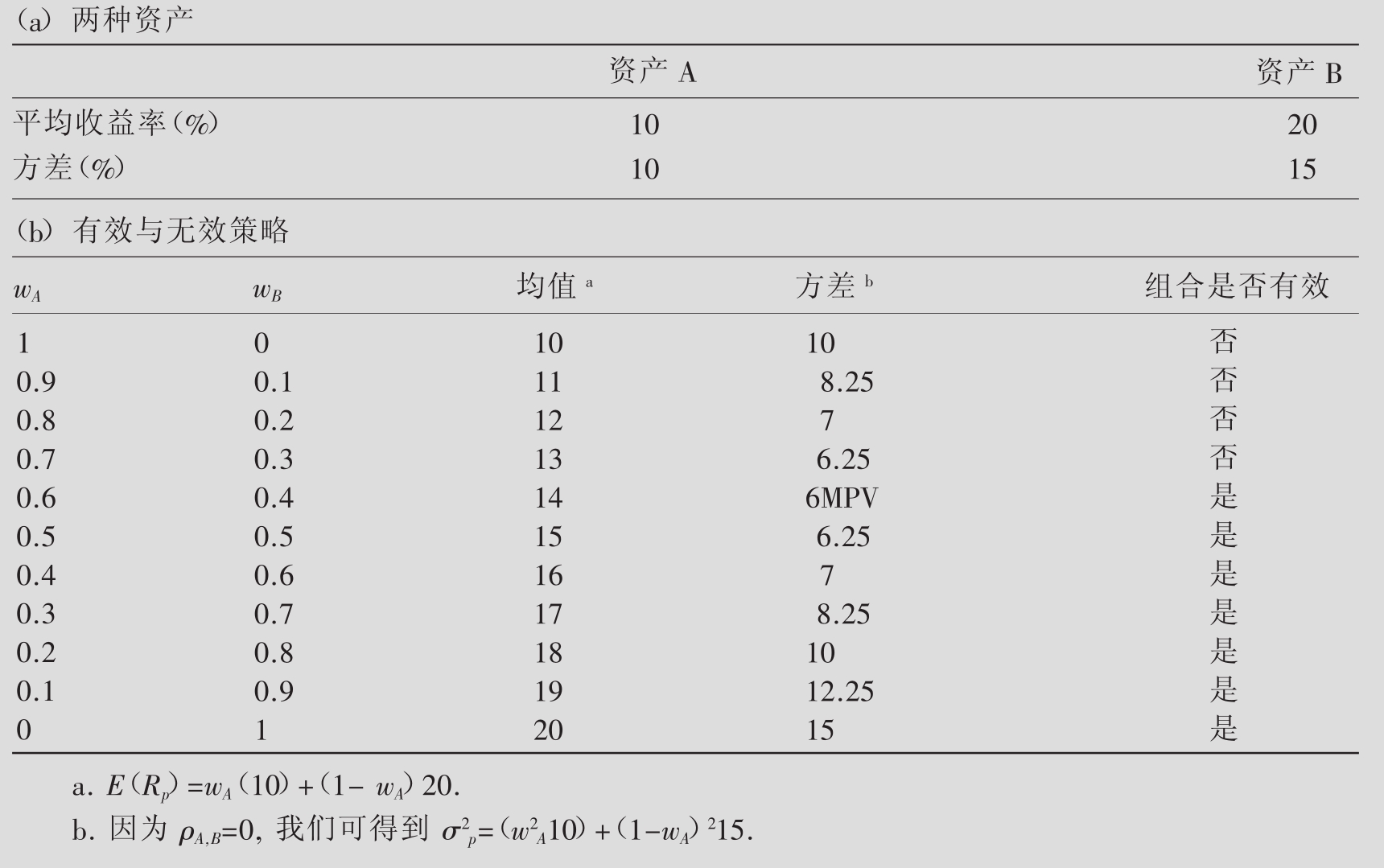
表8.7列出了两个不相关的资产A、B的均值和方差。它们都可以用直接法计算（用方程8.5和8.6）。而当个人的各种可能状态下的收益并不知道时，就不能应用直接法了。如表8.7所示，随着资产组合中具有较低期望收益的资产A的比例的下降，资产组合的期望收益率将增加。这一结论是很显然的，因为对高期望收益的资产将投入更大的比例，所以减少对资产组合的均值影响是明显的：投资于资产B的比例越高，资产组合的期望收益就越大。在w_A=0，w_B=1的极端情况下，资产组合仅由资产B组成，其平均收益率是20%。

表8.7　资产相关系数为零时的有效和无效边界

资料来源：利维：《投资学入门》第二版。

方差的变化就没有这么直观了。首先，当减少（增加）时，资产组合的方差先是下降，并在w_A=0.60时达到其最小值，然后才开始增加。对应于w_A=0.60的资产组合称之为最小方差投资组合（MVP，Minimum Variance Portfolio）。该组合是在均值—方差边界上具有最小方差的资产组合。资产组合的方差和投资比例之间的关系一般向纵轴弯曲（除了ρ_A，B=-1，ρ_A，B=+1，或其中一个资产是无风险的极端情况）。结合均值与方差，可见并非所有的分散化投资都是有效的。特别地，当w_A>0.60时的投资战略是无效的，因为可以通过w_A≤0.60的战略获得更高的期望收益及更低的方差。例如，w_A=0.70、w_A=0.80、w_A=0.90以及w_A=1.00的投资战略都比w_A=0.60的最小方差投资组合具有更低的均值和更高的方差。

图8.8用图形说明了表8.7的结果。曲线AB描述了由资产A和B的不同比例构成的投资组合的均值和标准差，其中点B对应于100%投资于资产B，点A对应于100%投资于资产A。随着投资于资产A的比例不断下降，资产组合的均值将增加，然而方差则在到达点MVP之前不断减少，然后开始增加。该图明显表明，没有投资者会选择低于点MVP的投资组合，因为对于这些投资组合，至少存在点MVP以上的一个投资组合比它更好——该组合具有更高的期望收益和更低的方差。考虑资产组合p，因为组合p′与p具有同样的方差，而其均值却更高，所以组合p′优于组合p。对于具有无差异曲线（更为陡峭的无差异曲线）的投资者，组合p是最优的；对于一个胆小的投资者，投资于组合p比p′使之处在一个更低的无差异曲线上，所以情况变差。

图8.8　两证券的资产组合

资料来源：利维：《投资学入门》第二版。

虽然AB是均值—方差边界，但仅有一部分是有效边界。低于点MVP的部分则是无效边界（Inefficient Frontier），它对应于无效的投资战略。也就是说，至少存在一个处于点MVP之上的投资组合能获得更高的期望收益及更低的方差。高于点MVP的部分称之为有效边界（Efficient Frontier），它对应于有效的投资战略。任何处在点MVP以上的投资组合都有可能成为投资者的选择，因为不存在其他的组合优于它。例如，我们对比p′和p″，p″比p′具有更高的均值和更高的方差，所以p′与p″都不优于对方。但是对于具有无差异曲线I_t的投资者而言（胆小的投资者），投资组合p′是最优的；对于具有无差异曲线I_t（更平坦的无差异曲线）的更具冒险性的投资者而言，投资组合p″是最优的。处在点MVP之上的所有资产组合都具有这样的特点。

我们常用实线来表示曲线的有效部分，虚线来表示无效部分。没有投资者会选择虚线上的投资组合，因为对于这些资产组合，总存在另一个与之具有同样标准差，并具有更高均值的更为有利的组合（处在虚线上方的实线上）。值得注意的是，100%由最高均值和最低方差资产（资产B）构成的资产组合是有效的，而100%由最低均值和最低方差资产构成的资产组合一定是无效的。风险规避的投资者一般持有分散化的投资组合——同时包含资产A和B。然而一个具有极低风险规避的投资者将会仅投资于具有较高均值的资产或资产B。

8.3.2　具有不同相关性的两资产组合

本节将说明，在两资产情况下，其相关系数是如何影响均值—方差边界的。表8.9除了分别对比了四种不同相关性，ρ_A，B=-1，-0.5，+0.5和+1的资产A和B外，基本上与表8.7一致。ρ_A，B=-0.5和ρ_A，B=0.5得到的结果与ρ_A，B=0时非常相似，唯一不同的是，从ρ_A，B=+0.5情况下的分散投资比ρ_A，B=0时获利更多，而当ρ_A，B=-0.5时将比ρ_A，B=0时获利更少。例如，在一个均值为12%的资产组合中，当ρ_A，B=-0.5时，其方差是5.04；当ρ_A，B=+0.5时，其方差是8.96；当ρ_A，B=0时，方差是7。一般地，在其他条件不变的情况下，ρ_A，B越大，从分散化投资中所得就越少。

表8.9　当两资产相关系数处于不同水平时，资产组合的均值和方差情况

资料来源：利维：《投资学入门》第二版。

图8.10根据表8.7和表8.9描绘了普遍存在的资产相关性对有效边界和无效边界的影响特征。当ρ_A，B=+1时，有效边界是一条直线——AB——所有处在这条直线上的投资战略都是有效的。当ρ_A，B=-1时，从点B到点MVP的线段是有效投资战略集，而从点MVP到点A的线段则是无效的。这两条直线交于纵轴，表明通过安排适当的投资比例，我们可以获得无风险（零方差）的资产组合。当相关系数处在-1与+1之间时，将得到一条弯曲的有效边界。然而，随着相关系数的下降，曲线越向左凸，这意味着分散化越能降低风险。

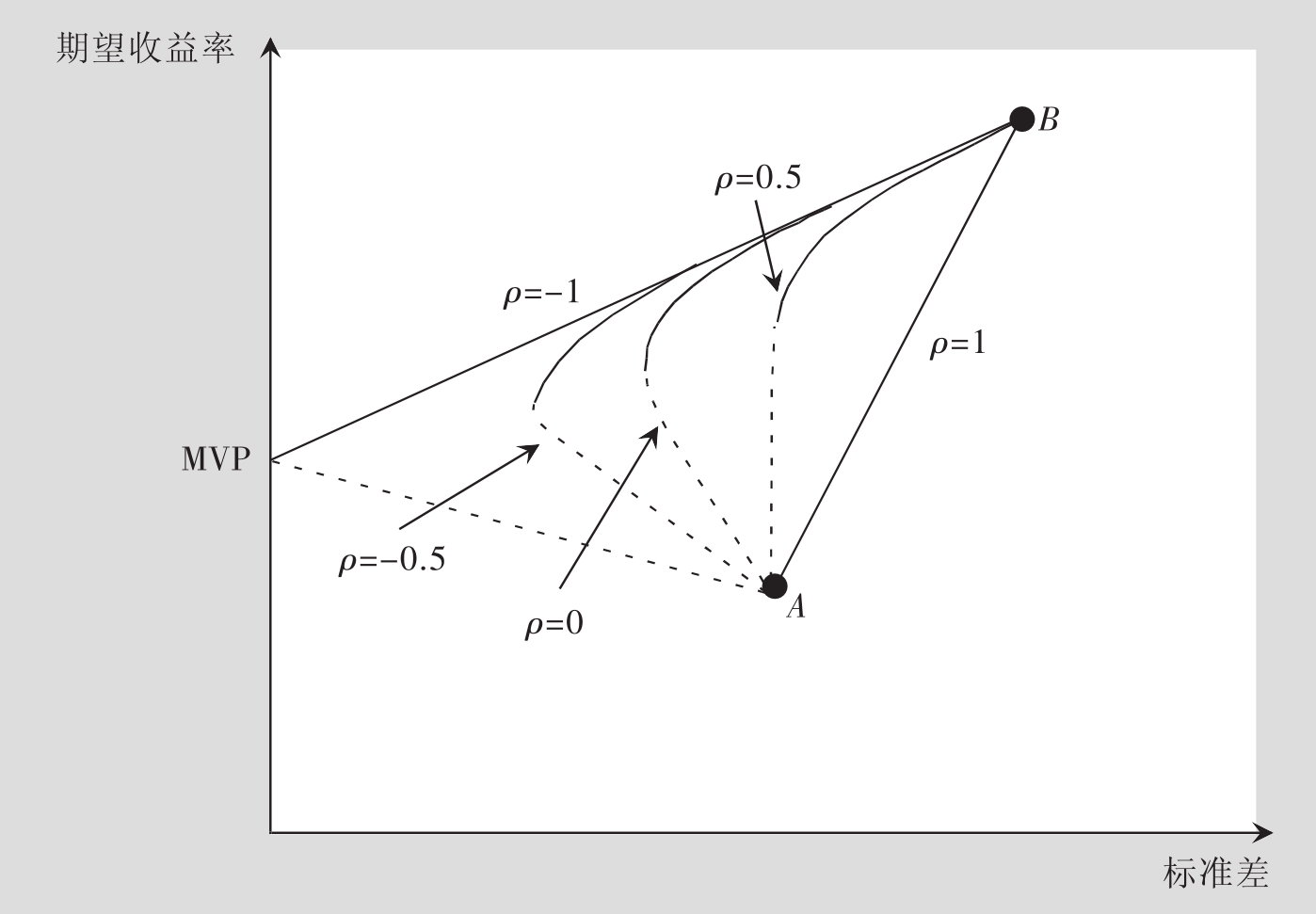
图8.10　相关系数对有效和无效边界的影响

8.3.3　多资产情况下的有效和无效边界

至此，从两个资产的分析中已显示出分散化投资带来的好处。该分析得出，均值—方差边界就是所有均值—方差概率组合之集（或均值—方差概率组）。任何可能的投资组合都能从均值—方差边界上找到。由于在实际中，投资组合所含的资产数目一般大于两个，那么投资组合选择就复杂些。我们首先要找出其均值—方差边界，然后再区分边界的有效和无效部分。

在多资产的情况下，投资者可以找到处于均值—方差边界上的投资战略和处在边界内的投资战略——在边界右方的投资战略。图8.6标出了A～E五种资产。投资者可以用至少两种资产的组合来进行分散化投资，从而获利。图形上显示了三个这样的分散战略AB、CD和DE，它们都用“2”标出，表明这些组合都是由两个资产构成的。当然还有其他的一些两资产投资组合（如，AE），但是为了简单起见，它们都没有在图中标出。同样的，分别标以“3”、“4”、“5”的曲线则分别表示由三、四或五个资产组成的投资组合。所有这些可能的分散化投资战略数目是无限的。^[16]

在给定平均收益率的情况下，曲线5相对其他的曲线具有更低的标准差，所以它是均值—方差边界。应当注意，对于任意的一点p，在曲线5上总存在一点p′，使得它获得与p同样的均值和更低的标准差。只有曲线A—MVP—E的一部分是均值—方差有效的：从MVP到E的这一部分是均值—方差无效的，而从MVP到A的部分才是有效的。

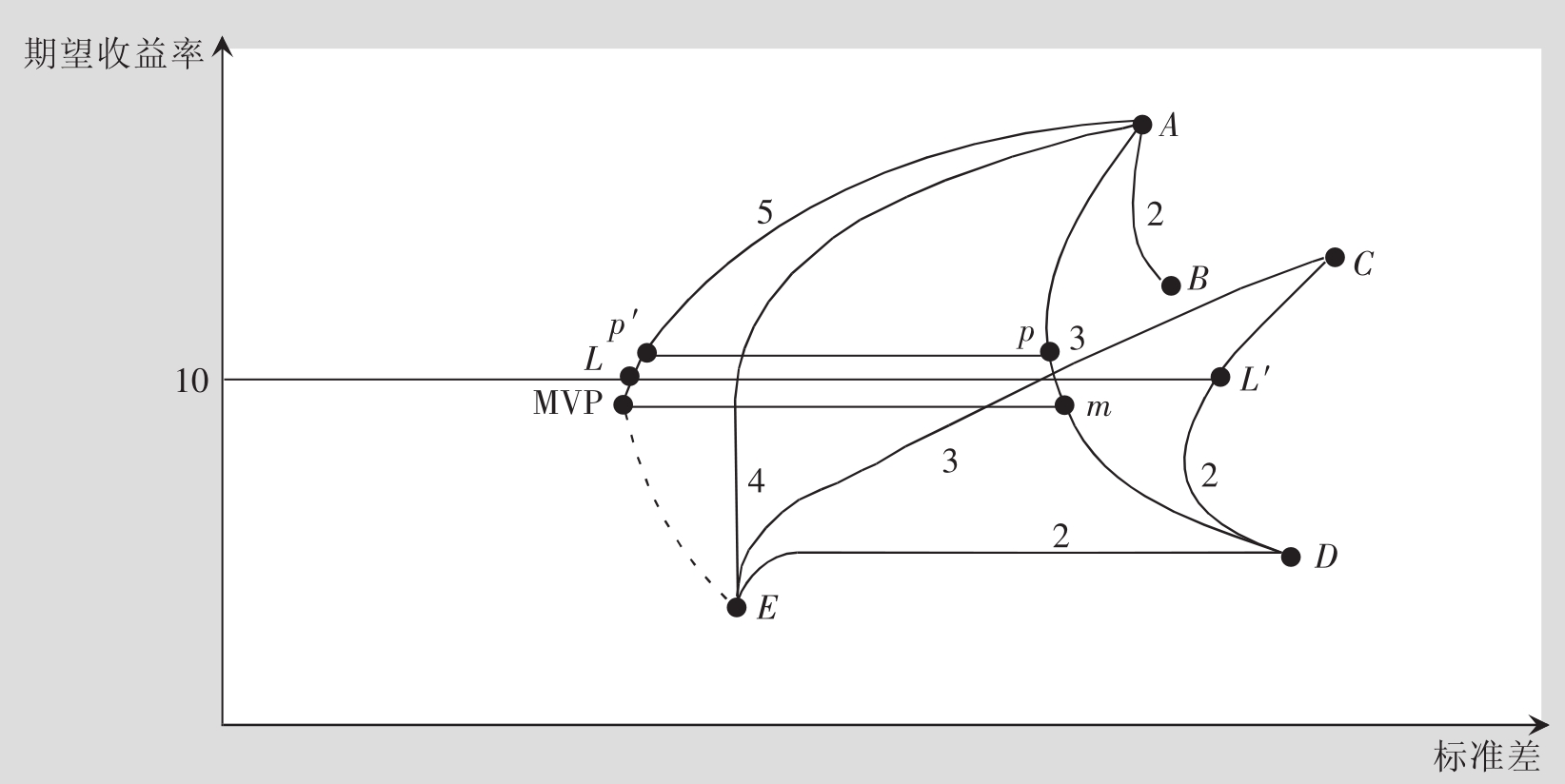
图8.11　多资产情况下的有效和无效边界

与只有两种资产的情况不同，由多种资产构成的一些投资组合虽然是可行的，但并不一定处在均值—方差边界上。比如点D，曲线2、3、4等，都处在边界内部。由于没有投资者会选择均值—方差边界内部的资产组合，寻找最优资产组合的最好方法是：首先确定均值—方差边界，然后再区分边界的有效和无效部分。

8.3.4　寻找均值方差边界

在本章中，用图形表示有效边界虽然很简单，但是要找到对应的边界组合中各种资产的权重就不是一件简单的事情了。计算要借助于标准的电子数据表格软件才能完成。

要确定有效边界需要解决下面的问题：求出组合权重w₁，w₂，…，w_n，使得资产组合的方差

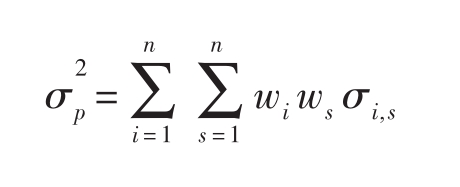
在约束条件

和

下，达到最小。当然，约束条件还可能增加，比如卖空限制（见下面）。^[17]

假设一个投资者希望通过一个资产组合获得E（R_p）=10%的平均收益，所有处在LL′（见图8.14）上的分散化投资战略都可以达到这一目的。通过使资产组合的方差σ2 _p最小，可以求出对应于均值—方差边界点L的投资战略。也就是说，不存在具有平均收益为10%且具有更低方差的投资组合，所以点L代表了一个边界组合。

对于另一个E（R_p）=11%，重复上述的求解过程，我们可以得到另一个边界点p′。不断改变的值，可以得到均值—方差边界和投资战略的有效集。在一个特殊的情况下，有效边界就是从点MVP到A的这部分（见图8.11）。

必须清楚，均值—方差边界的形状依赖于各个投资的均值、方差及协方差，而且也依赖于施加在投资组合权重的限制条件，例如，在7.1节讨论的资产组合可能集。如果对其限制条件越多，投资者能选择的投资战略就越少，那么边界情况就会恶化。例如，（在给定方差下）最大的可能均值减少，（在给定的均值下）最低的可能方差会增大。同样的，减少投资的限制条件可以获得更多可行的均值—方差组合，从而使均值—方差边界得到改善。第10章将证明，在允许投资者以无风险利率借贷的情况下，如何扩大投资机会。表8.12、表8.13、图8.14表明了，解除卖空限制（允许投资者卖空资产），对均值—方差边界的影响。

表8.12对五个主要资产组（大盘股票、小盘股票、长期公司债券、长期政府债券和中期政府债券）的期望收益、标准差以及它们之间的相关系数作了历史的估计。

表8.12　五大类美国主要资产的历史估计（基于1926～1996年的年度收益率）

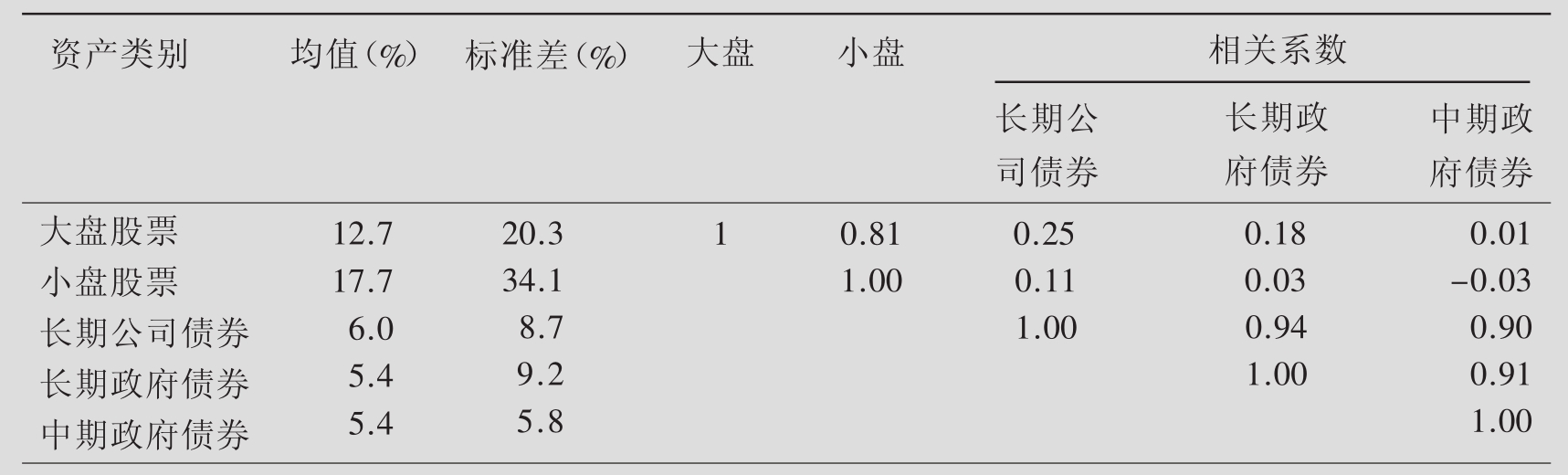
资料来源：Ibbotson协会：《股票、债券、票据和通货膨胀年报》，1997年。

表8.12常用来确定在有卖空或没有卖空情况下的有效边界。正如7.1节所述，可以增加w_i≥0的条件来排除存在卖空的情况，而表8.13（b）说明了不存在卖空时，几种有效资产组合的构成，图8.14则用图形说明了存在卖空与不存在卖空的均值—方差边界的差异。如图所示，存在卖空的有效边界优于没有卖空时的情形。因为当w_i为负时（投资者当然也可以取得w_i≥0）投资者将获得更多的投资机会，所以卖空边界在非卖空边界的左面。例如，当存在卖空且均值为7.1%时，最小可能标准差为5.7%；相反，当卖空不存在时，最小可能标准差增加到6.7%，可见卖空可以改善有效边界。

表8.13　有效边界：存在和不存在卖空

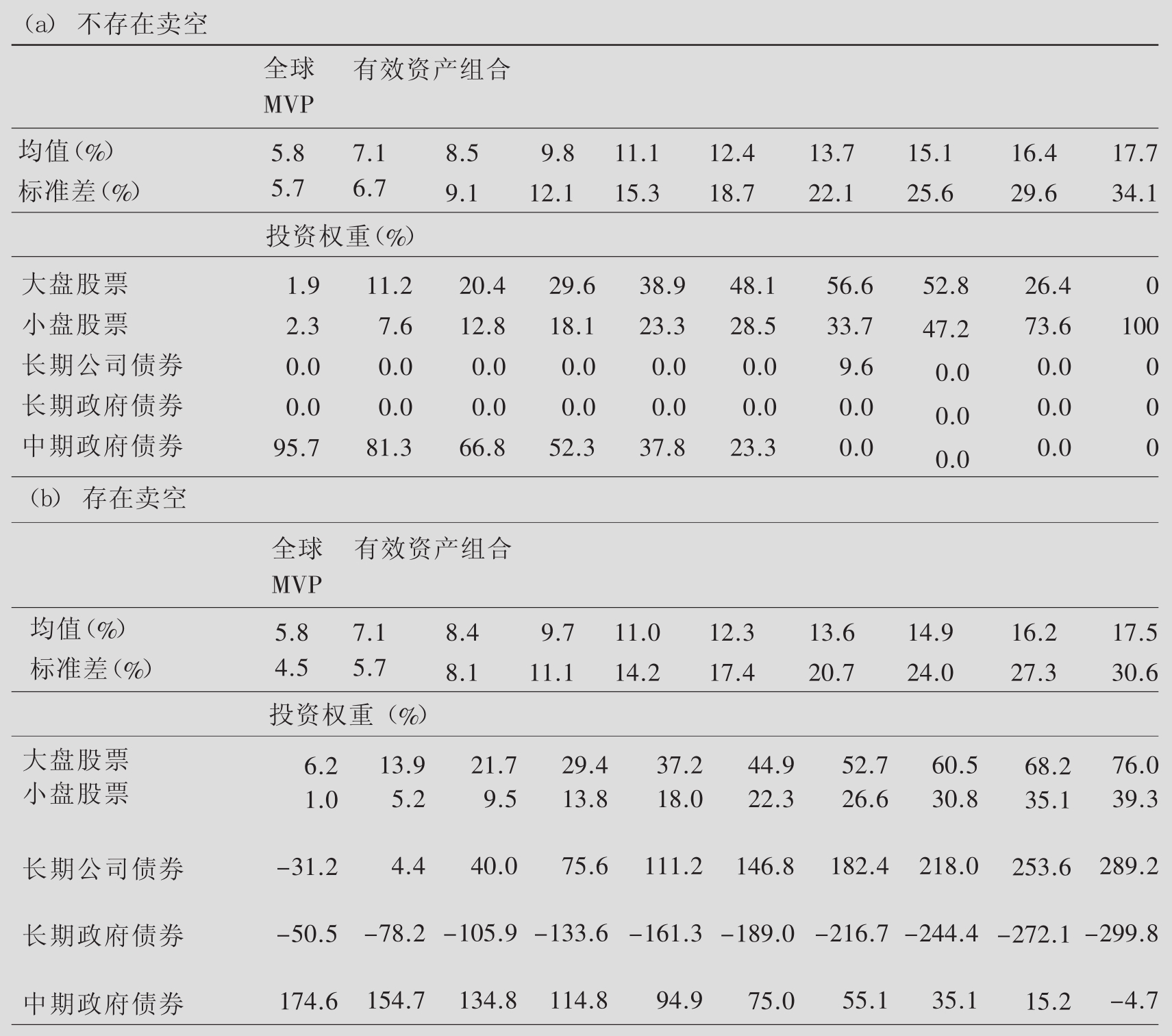
资料来源：利维：《投资学入门》第二版。

上面的例子表明，均值—方差边界的具体形状依赖于对资产组合权重的限制条件。也就是说，只要低收益资产与其他高收益资产之间相关性弱或负相关，它们仍能成为很有吸引力的投资对象。表8.12就列出了在历史上具有很低平均收益的债券，投资者同样应当对这些证券给予重视，因为这有助于分散化投资。例如，在表8.13（a）中，假设没有短期买卖，考虑目标回报率为11.1%，除38.9%投资于大盘股，23.3%投资于小盘股外，另外，37.8%的资金要投资于中期政府债券，它的平均回报率为5.4%。表8.13（b）说明在卖空存在时，也将得到同样的结果。

最后必须注意到，例子中得到的有效边界是基于对均值、标准差和相关系数的历史估计。在未来，实际的均值、标准差及相关系数有可能与之发生很大的变化，所以真正的有效资产组合的构成可能与表8.13，图8.14显示的有很大的不同。下一章将更为精确地讨论参数估计问题。

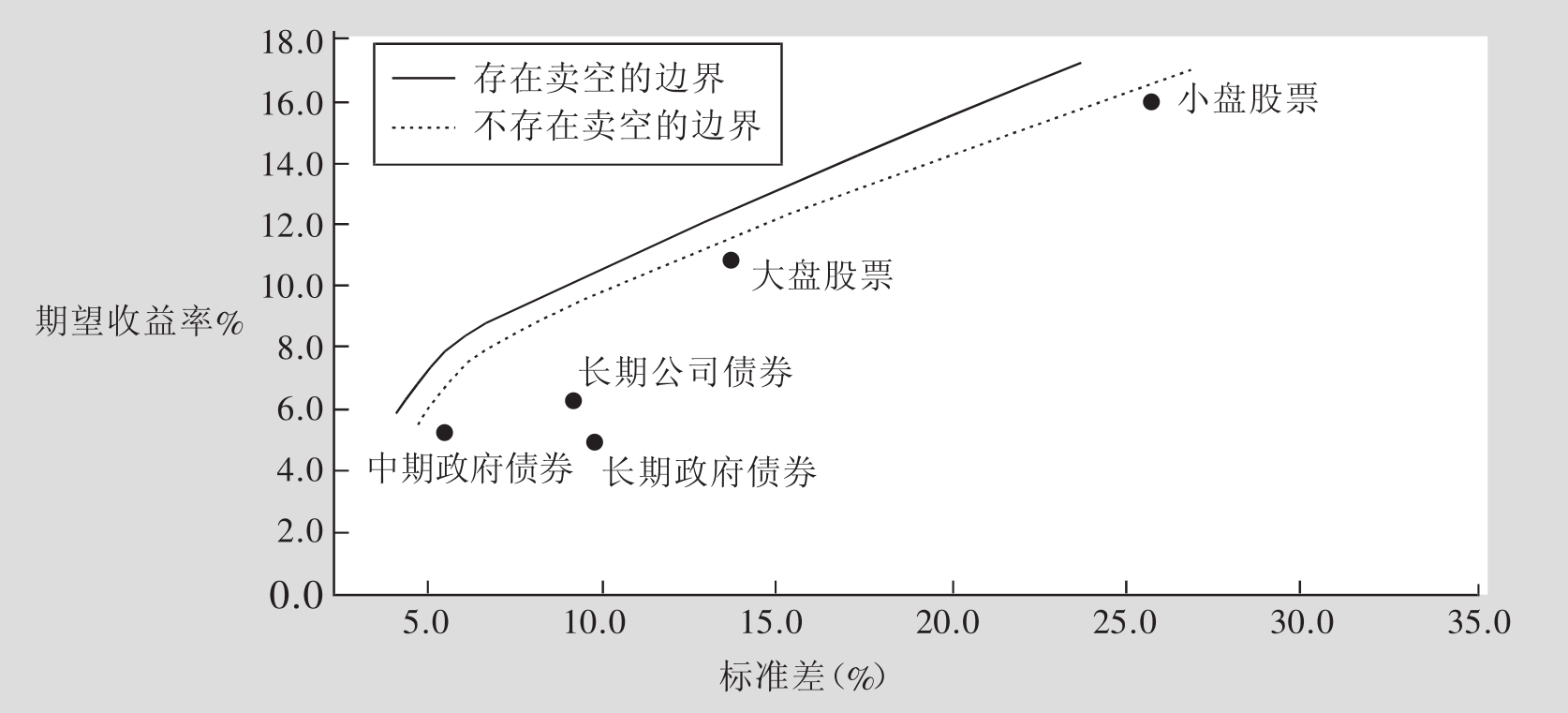
图8.14　存在卖空与不存在卖空时的有效边界

资料来源：利维：《投资学入门》第二版。

总结

资产选择中的均值—方差标准

均值—方差标准（MVC）提供给我们在风险资产间做出选择的一个简单方法。MVC认为投资者①在具有相同（或更高）的期望收益时，会偏好最低的方差；②在具有相同（或更低）方差时，偏好最高的期望收益。

均值—方差理论的经济意义

均值—方差理论是一般期望收益理论的一个近似。期望收益理论说明了资产组合可能集、资产收益概率分布和投资者效用函数之间的一般关系。但在实际中，期望效用理论不具有可操作性，而均值—方差理论则提供了一种可操作的近似方法。如果收益近似服从正态分布或者效用函数能用二次函数近似，那么均值—方差则是一种较好的近似方法。在这两种条件下，投资者仅需要关注资产组合的均值和方差。一般来说，在实际中至少有一个条件是满足的，所以均值—方差分析是一般期望效用理论的一个很好的近似。

计算资产组合的均值及方差的两种方法

直接法是计算资产组合均值和方差的最简单的方法，该方法用单个资产的收益和权重来计算各种可能状态下的资产组合收益，然后利用与计算单个资产同样的方法来计算资产组合的均值和方差。然而，除非我们拥有在各种可能状态下所有单个资产的收益，否则该方法就行不通。间接法却可以避免这个问题，通过计算单个资产均值的加权平均得到资产组合的均值，并利用单个资产方差及协方差来计算资产组合方差。虽然用间接法计算方差比用直接法复杂得多，但是其对信息的要求较低——不需要知道单个资产收益观测值，并且间接法还使我们能更深入地理解资产组合方差的决定以及分散化的影响。

确定有效和无效投资战略

运用均值—方差标准，投资者将会选择均值—方差可能集子集中的资产组合。该集合就称为有效均值—方差边界。因为面对相同（或更高）的期望收益，投资者偏好最低的方差，他们仅关注在给定均值下具有最小方差的资产组合，或均值—方差边界。均值—方差边界可分为两部分：有效边界和无效边界。有效边界是指在给定方差下具有最高均值的资产组合。而为了得到有效边界，必须利用电子数据表格程序解一个二次优化问题。

关键词

协方差237

均值—方差有效236

正态概率分布231

直接法237

均值—方差理论230

资产组合均值237

均值—方差边界241

期望效用理论230

效用均值—方差边界241

资产组合方差237

无差异曲线234

均值—方差无差异曲线234

二次函数231

间接法238

均值—方差概率组241

二次效用函数233

有效边界241

最小方差投资组合（MVP）242

标准差231

均值—方差效率标准236

方差237

无效边界241

正态分布231

练习题

1.a.总结均值—方差有效标准。

b.这一标准与均值—方差有效边界的关系是什么?

2.a.如何计算资产组合的期望收益率和方差？

b.说明资产组合中单个资产的风险。

c.解释协方差。

d.相关性在资产组合中所起的主要作用是什么？

3.计算资产组合均值和方差的两种方法是什么？这两种方法分别在什么情况下适用？

4.下表中给出了股票H和I的收益概率分布。

考虑投资5000美元于股票H，且投资15000美元于股票I的资产组合，运用直接法和间接法计算该资产组合的标准差。

5.在下列条件下，有效边界将如何变化：

■存在卖空（开始假设不存在卖空）；

■额外资产的引入；

■资产间相关性提高。

若想获得练习题的参考答案，请访问Levy-Post投资网站，网址为：http://www.booksites.net/levy

参考文献

Arditti，F.D.，1971，‘Another Look At Mutual Fund Performance’，Journal of Financial and Quantitative Analysis，6，909-912.

Bawa，V.S.and E.B.Lindenberg，1977，‘Capital Market Equilibrium in a Mean-Lower Partial Moment Framework’，Journal of Financial Economics，5，189-200.

Bera，A.K.and C.M.Jarque，1981，‘An Efficient Large-Sample Test for Normality of Observations and Regression Residuals’，Australian National University Working Papers in Econometrics，40，Canberra，Australia.

Bigelow，J.P.，1993，‘Consistency of Mean-Variance Analysis and Expected Utility Analyses:A Complete Characterization’，Economic Letters，43，187-192.

Chunhachinda，P.，K.Dandapani，S.Hamid and A.J.Prakash，1997，‘Portfolio Selection and Skewness:Evidence from International Stock Markets’，Journal of Banking and Finance，21，143-167.

Fama，E.F.，1965，‘The Behavior of Stock Market Prices’，Journal of Business，38，34-105.

Hanoch，G.and H.Levy，1970，‘Efficient Portfolio Selection with Quadratic and Cubic Utility’，Journal of Business，43，（2），181-189.

Kraus，A.and R.Litzenberger，1976，‘Skewness Preference and the Valuation of Risk Assets’，Journal of Finance，31，1085-1100.

Levy，H.and G.Hanoch，1970，‘Relative Effectiveness of Efficiency Criteria for Portfolio Selection’，Journal of Financial and Quantitative Analysis，5（1），63-76.

Levy，H.and H.Markowitz，1979，‘Approximating Expected Utility by a Function of Mean and Variance’，American Economic Review，69，308-317.

Markowitz，H.M.，1952，‘Portfolio Selection’，Journal of Finance，7（1），77-91.

Markowitz，H.M.，1959，Portfolio Selection，New York:John Wiley&Sons.

Markowitz，H.M.，1987，Mean-Variance Analysis in Portfolio Choice and Capital Markets，New York:Basil Blackwell.

Samuelson，P.A.，1970，‘The Fundamental Approximation Theorem of Portfolio Analysis in Terms of Means，Variances，and Higher Moments’，Review of Economic Studies，37，537-542.

Simkowitz，M.A.and W.L.，Beedles，1978，‘Diversification in a Three-moment World’，Journal of Financial and Quantitative Analysis，13，927-941.

Singleton，J.C.and J.Wingender，1986，‘Skewness Persistence in Common Stock Returns’，Journal of Financial and Quantitative Analysis，21，335-341.

Tobin，J.，1958，‘Liquidity Preferences as Behaviour Toward Risk’，Review of Economic Studies，25，65-86.

Tsiang，S.C.，1972，‘The Rationale of the Mean-Standard Deviation Analysis，Skewness Preference and the Demand for Money’，American Economic Review，62，354-371.

【注释】

[1]More generally,mean-variance analysis is consistent with expected utility analysis for all so-called elliptical distributions;such distributions can be expressed in terms of their mean and variance alone.The normal distribution is one example of an elliptical distribution.

[2]The Jarque-Bera statistic is one way of testing the null hypothesis that a series is distributed normally（i.e.has skewness of zero and kurtosis of three）;see Bera and Jarque（1981）.

[3]A selection of studies of the statistical distribution of actual asset returns includes Fama（1965）,Arditti（1971）, Simkowitz and Beedles（1978）,Singleton and Wingender（1986）and Chunhachinda et al.（1997）.

[4]This phenomenon is called‘leptokurtosis’.Kurtosis is a statistical measure for the thickness of the tails.This measure is defined as E（R-E（R））⁴.For extreme returns（far below or far above the mean）,the term（R-E（R））⁴takes very large positive values.Hence,if a distribution has a high probability of such returns,then it will have a high kurtosis.

[5]The central limit theorem does not apply if the random variables are not independent.

[6]The central limit theorem does not apply if the random variables have a different distribution.

[7]The skewness of a distribution is measured as E（R-E（R））³.For returns far below the mean,the term E（R-E（R））³takes very large negative values.Hence,if a distribution has a high probability of such returns,then it will have a negative skewness.

[8]The shape of the return distribution depends on the investment horizon and the graph looks different if we use,for example,daily returns or yearly returns.One obvious reason is the effect of compounding returns.To see this,consider the hypothetical case where there is a 50%probability of a negative return of-10%and 50%probability of a positive return of+10%for a stock in each and every period.This return distribution is perfectly symmetrical around the mean of zero.If we consider the total return over two periods,then there is a 25%probability of two negative returns,yielding a total return of 0.9×0.9-1=-0.19,a 50%probability of one positive return and one negative return,yielding a total return of 1.1×0.9-1=-0.01,and a 25%probability of two positive returns,yielding a total return of 1.1×1.1-1=0.21.Clearly,this distribution is not symmetric around the mean of zero（0.25×（-0.19）+0.5×（-0.01）+0.25×0.21=0）;the maximum upside deviation of 21%is larger than the maximum downside deviation of-19%.Similarly,over very many time periods,the minimal possible return is-100%,while there is no upper limit.

[9]See，for example，Tsiang（1972）and Levy and Markowitz（1979）.

[10]It is common to refer to the mean and the variance as the first two central moments of the return distribution.If the range of returns is very wide，then higher-order central moments（such as skewness and kurtosis）may become relevant in addition to mean and variance.See，for example，Kraus and Litzenberger（1976）.If the utility function exhibits kinks，then the investor cares about lower partial moments（such as expected loss and semivariance）in addition to the central moments. See，for example，Bawa and Lindenberg（1977）.

[11]The parameter determines the intercept of the utility function;b determines the slope at R=0;and c determines the curvature of the function.To guarantee that the utility function is increasing（over a range），we must have b>0.（Notice that the function is increasing for R<-b/2c and it is decreasing for R>-b/2c.）Also，we need c<0 so as to impose risk-aversion.

[12]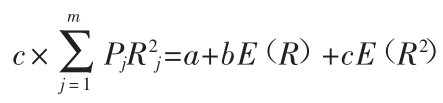④To see this，we first use the following chain of equalities: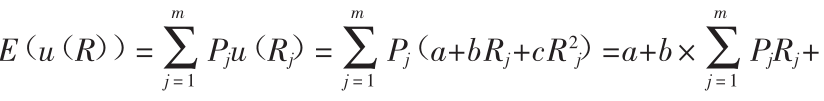.Next，using σ²=E（R）²-E（R）²，the last equality can be rewritten as E（u（R））=a+（b+cE（R））E（R）+cσ².

[13]We assumed c<0 in order to impose concavity.Hence，expected utility in Equation 8.1 is decreasing in variance. Also，we assumed that utility is increasing or u′（R）=b+2cR>0.Taking the expectation of both sides of the equation，we find E（u′（R））=b+2cE（R）>0 or c>-b/（2E（R））.This implies that the term b+cE（R）in Equation 8.1 is greater than b/2. Hence，expected utility is increasing in the mean.

[14]This particular quadratic utility function is obtained by a second-order Taylor series approximation around R=0. Specifically，we set a=u_A（0）=1，b=u′_A（0）=4 and c=u_A″（0）/2=-8.

[15]Again，if these conditions are considered too restrictive，then the framework of stochastic dominance offers an alternative to mean-variance analysis.See the references in Section 7.6 for more information.

[16]To understand this，it is useful to rewrite Equation 8.1 as σ²=-E（u（R））/c-a/c-（b/c）（E（R）-E（R）²）.If we fix the level of expected utility E（u（R）），then this expression gives the variance σ²as a function of the mean E（R）；it gives the indifference curve for E（u（R））.By taking the first-order derivative of σ²with respect to E（R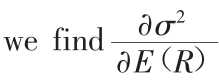），w=-b/c-2E（R），which is the slope of the indifference curve or the additional units of variance that the investor will accept for a unit of additional expected return.By taking the first-order derivative of σ²with respect to E（R），we find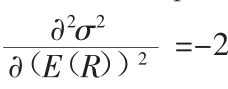，which is the curvature of the indifference curve.The curvature is negative，which means that the additional units of variance that the investor will accept for a unit of additional expected return decrease.Put differently，the additional units of expected return required to compensate for a unit increase of variance increase.Note that variance is a concave function of mean return（the second-order derivative is negative），or the mean is a convex function of the variance（the second-order derivative is positive）.