投资组合资产收益率

第10章　资本资产定价理论

投资新闻10

FT

估算预期收益比重的模型博弈

要高估预期收益在投资中的重要性是一件困难的事情，对货币基金经理人而言，对证券的预期收益是重要的投资决策依据；对公司经理而言，该公司股票的预期收益则是公司资本成本的核心问题，公司资本成本进而又会影响到公司的投资决策。预期收益的估算对消费者同样有影响。公用事业公司索要的费用是用来确保这些公司可以“赚取合理的收益”，这个向消费者索要的费用被管理者们界定为公共事业资本成本。我们收到的能源使用费账单中，就有一部分是取决于管理者是如何估算公用事业股票的收益水平的。不幸的是，预期收益很重要，但也很难以捕捉。金融领域的专业人士，对于应当如何估算公用事业股票的预期收益值意见不一，这篇文章将比较各种计算预期收益值的一般方法具有的优点，并最终认为，只有把能描述历史收益水平数据的理论和自己的判断联系到一起，才可以做出最好的预期收益评估。

向历史看齐

美国独立战争时期的革命者帕特里克·亨利（Patrick Henry）曾经说道：“我只知道历史是判断未来的唯一方法。”一种简单的预期收益评估指标就是历史收益的样本平均数。除非我们怀疑预期收益值会随着时间的推移而发生不小的变化，否则历史收益的样本均值仍然是一个客观而没有偏差的预期收益估算指标，也就是说，这个指标不会系统性地高于或低于真实的预期收益。然而，用均值来预测未来可不是唯一的目标。你可能曾经听到过一个笑话，说的是有三个经济学家一起去打猎，遇到了一只鹿。第一个经济学家放了一枪，没有打中，因为向左边偏了10米。第二个经济学家又开了一枪，也没有打中，因为向右偏了10米。第三个没有开枪，他以胜利的语气大声喊道：“我们打中了！”样本均值最主要的不足就是它还不够精确。假设我们要预测GM公司的股票将会是什么样的预期收益，该股票在纽约证券交易所交易。用1991年1月～2000年12月期间的月度收益来计算，该公司股票的样本平均收益是每年14%，标准误差是用来计量不准确性的指标，在这个结果中，标准误差的值很大，达到了每年10%。用95%的置信区间来衡量，真正的预期收益应该是在样本均值的两个标准误差之间，也就是说每年的真正收益率应该在6%～34%。需要比这个数值区间更加让人信服的精确数据！如果用周收益数据而非月度收益数据来计算的话，结果会不会更加精确呢？答案是不会的。尽管更高的数据收集频率对估算收益的方差和协方差会有帮助，但是它却不能帮助估算预期收益。凭直觉就知道，就预期收益而言，重要的是某一段时期的初始价格和收尾价格，而非是这段时间内发生了什么样的价格变动。要得到更精确的平均数，唯一的办法就是收集更多的数据。比如说，在上面那个例子中，如果我们用的数据是从1925年12月开始记录的，历史平均收益就是15.5%，这个数值的95%置信区间也会缩小到8.7%～22.3%之间。尽管如此，这个区间仍然太宽泛了。此外，今天的GM公司和70年以前已经有了很大的差别。所以，这个估值可能会被旧数据污染。一般来说，当加入旧数据时，都会提高估算的精确度，但这样做的代价就是，可能由此而引入潜在的偏见。打破平衡是一件难事，而且需要靠得住的判断。尽管有很多的局限，长期平均收益值仍然是最常用来评估总体市场指数预期收益值的评估指数。不幸的是，我们还没有理论可以说明，预期市场收益应该是怎么样的。幸运的是，对大多数投资组合以及单支股票而言，可以用理论性证券定价模型来做出预期收益评估。这样得来的估算值会大大精确于用样本均值得出的值。

资料来源：罗伯斯·帕斯特：《估算预期收益比重的模型博弈》，《金融时报》2001年5月21日。

学习目标

在完成本章的学习后，你应能够：

1.理解资本市场界限，它包含有效投资组合。

2.解释分离原则。

3.理解为什么证券市场界线描写了资本证券和预期收益间的平衡关系。

4.解释用来检测资本证券定价模型的双重传递回归法。

5.理解为什么检测资本政权定价模型是否能很好地描写资本市场是一件很困难的事情。

6.理解证券交易从业人员是如何运用资本证券定价模型的。

第8章讨论了如何以平均方差分析作为投资决策的理论框架。在那章里，讨论了在预期收益、方差和单证券间协方差一定的情况下如何制定投资策略的问题。然而，却没有怎么谈到预期收益率是如何决定的。资产定价理论（Asset-pricing Theories）试图理解为什么有些证券的预期收益会比其他证券的高，以及为什么同一个证券的预期收益在不同的时间点上会有不同的值。比如说，回忆一下第6章里讲到的：历史上股票带来的收益高于同一时期内长期国债和短期国债带来的收益。我们如何解释这种差异呢？

各种资产定价理论都试图解释各种各样的均衡收益率（Equilibrium Rates of Return）。“均衡收益率”指的是什么呢？首先，它只是一种方便的表达方式，用来表示各证券间的相对价格。比如说，和实际价格不同，预期收益不会受绝对价格水平的影响，也不受该公司未结清的股票数目多少影响。比如说，一支股票一分为二，股票价格在这种情况下典型地也会下跌50%，但是预期收益却不会变。与其他一切商品和服务的价格一样，资产的价格和预期收益决定于供求关系的情况。如果有很多投资者决定售出某支股票，那么在其他条件都相同的情况下，这支股票的价格就会降低（而预期收益则会升高），以便适应供求关系的对应状况。如果所有的证券价格（或者预期收益）刚好能让所有的证券供求相等，那么资本市场就处于平衡状态了。换一种说法，如果所有的投资者都持有最佳投资组合，进而没有理由再进一步交易，那么市场平衡就会大行其道了。如果某些投资者，比如说因为他们适应新经济环境的速度比较缓慢，可能就没有办法持有最优投资组合。那么，他们依然想要购进或者卖出证券，从而改变了证券供求关系，进而也改变了证券市场价格（以及预期收益率）。

资产定价理论可以帮助人们理解资本市场中一些最重要的力量。此外，这些理论也被广泛地运用于投资组合选取、证券表现评估、风险管理以及资本预算等领域。在《投资新闻10》中，罗伯斯·帕斯特作为芝加哥商业研究院的一名副教授，解释了理论性的证券定价模型是如何被用来估算股票预期收益的。用这种方法得出的结果会大大精确于用平均历史收益得出的评估结果。

学术界有很多种不同的资产定价理论，这些理论都建立在一套各自不同的假设基础之上。本章主要讨论资本资产定价模型（CAPM，Capital Asset-pricing Model），这个模型是最基本的资产定价模型。这个模型是夏普（Sharpe，1964）、林特勒（Lintner，1965a，b）和莫辛（Mossin，1966）独立研发的。资本资产定价理论是建立在几个非常简单化的假设之上的。基本上，这个理论提出了以下几个问题：如果所有的投资者都把均值方差标准运用到一个完全相同的均值方差效率集上，收益均衡收益率又会是什么样呢？

现在，学者们正在争论这个理论是否精确地描述了收益均衡收益率，以及其他理论是否会作出更加合适的描述，这个争论还会持续下去。此外，很多其他的资产定价模型（包括一般资本资产定价模型（GCAPM）和多时间段资本证券定价模型（ICAPM），都可以被看成是对资本资产定价模型的综合概括。因此，资本资产定价模型就成了一个学习资产定价理论的自然出发点。

我们对资本资产定价模型的讨论将会用到均值方差里用过的术语，其中均值方差分析已经在第8章中介绍过了。此外，我们还会用到两个附加的概念：无风险资产（Riskfree Asset）和市场投资组合（Market Portfolio）。

资本资产定价理论向投资过程里加入了无风险资产这个因素。投资者可以无风险利率借出或贷入资金，此处的无风险指的是归还借出的资金是必然的。股市从业人员通常以短期国债的收益率作为无风险利率。此处我们用r表示无风险利率。当投资者借出资金的时候，他们就可以有效地持有一种证券的长期账务，也能从投资中赚取比率为r的收益。类似地，当他们贷入资金时，就能有效地清空无风险资产，并且付给债权人比率为r的利息。既然r肯定能按时给付（或支付），那么该证券的预期收益E（r）＝r，此外，无风险资产的方差以及它与其他资产间的协方差都是0。^[1]

市场投资组合是一个包含资本市场里所有能接纳投资的风险资本资产的组合，在这个组合中，各资产的权重是按照它们各自相对的市场价值来分配的（相对市场价值也就是用单支资产的市场价值除以所有市场中资产的总市场价值而得到的数值）。市场投资组合有以下三大属性：

■市场投资组合中包含有世界资本市场里所有的风险资本。它不仅包括股票和国债，还包括非金融性资产，比如说房地产、商品和人力资源（也就是未来劳动收入的当前价值）。当然，在实际操作中，我们并不是总能完全知道全世界所有资产的预期收益和市场价值是怎样的，因而需要一个样本来代表市场投资组合。一般而言，这种代表就是一个市场投资组合，比如说S&P500指数。需要强调一下：这种股指是一种狭义的市场组合，因为它不包括，比如说低封顶的股票，被投资者偏爱的股票、国债、房地产、商品、非金融性证券以及非美国证券。

■既然投资的市场价值不能小于0，市场投资组合中的所有资产都应有一个正的权重。因此，为了重复市场投资组合，一个投资者不用卖空任何资产。

■既然每一资产都有可能出现在某些投资者的投资组合中，市场投资组合也就可以被视为所有投资者的投资组合之和。具体而言，资产的相对市场资本等于该资产在所有资产组合中所占的比例。当然，既然世界上所有的资本资产都包括在市场组合中了，术语“投资组合”与“投资者”从更宽广的意义上说，就应当能互相换用。实际上，就算是一个婴儿，尽管他从来没有读过金融方面的报纸，也从未留意过电视里的商业新闻，同样会在人力资本投资组合中被划分为一个投资者。

本章接下来的内容安排如下：10.1节介绍了资本资产定价模型背后的理论基础。10.2节讲的是有关检验资本资产定价模型效度的一系列实证研究。资本资产定价模型是否能准确地描述历史收益率呢？或者这个理论的效度到底是不是可以检验呢？10.3节讨论了资本资产定价模型的实际运用。

10.1　理论基础

这一节将介绍资本资产定价模型的理论依据。为了便于分析，在此列出了资本资产定价模型三个最重要的理论暗示：

■在市场均衡的状态下，所有投资者都持有风险性资产市场组合，而不论他们的投资偏好是怎样的。但是，不同的投资者会用不同的方式联合持有市场组合和无风险性资产。资本资产定价模型的这个属性称为“分离原则”（Separation Principle）。

■既然每个投资者都持有市场投资组合，单独的资产有什么样的风险水平特征，就将由它与市场间的协方差决定。剩余的风险可以通过多样化投资组合来消除。计量该资产与市场间协方差的计量工具称为市场β值。β值既是用来表征单支资产风险的正确计量工具，也是用来表征投资组合风险的正确计量工具，无论这个投资组合是否有效都是如此。然而，对有效率的投资组合（市场组合与无风险资产的组合）而言，投资者用β值或者方差（或标准差）来计量这个投资组合的风险都是可以的，这两种计量方法都不会影响投资组合的风险排序。

■既然非系统性风险可以通过多样化来消除，投资者就应当为承担系统性风险（可以由市场β值来衡量），而不是非系统性风险获得补偿。证券市场界线（SML）就是这个原则的公式化体现，这个界线将该资产的预期收益和其市场β值联系到了一起。

10.1.1　资本资产定价模型背后的理论假设

■资本市场以完全的竞争为特征。资本市场中有大量的投资者，每个投资者拥有的财富相对于所有资本资产的总市场价值而言是很小的。因而，单个投资者的投资组合选择并不会给产权市场价格带来明显的效果，投资者只有接受这个价格。

■所有的投资者都依据均值—方差标准来选择自己的投资组合，也就是说在他/她对均值、方差和证券间协方差期望一定的情况下，以及他/她的投资偏好一定的情况下（这个情况可以通过个人均值方差无差别曲线来表示），每个投资者都会根据最优的均值方差效率来选择最优的投资组合。注意，均值方差标准忽略了很多实际的因素，比如说交易成本和税收。

■就均值、方差和协方差而言，所有的投资者对未来的期望都是一样的（同源性预期）。因此，每个投资者都会面对相同的均值方差投资组合概率集和相同的均值方差效率集。这个假设要求所有的投资者都有办法获取相同的信息。同样，所有投资者的投资时间跨度也都被假定为是一样的。因为一般而言，不同的投资时间跨度，会使得收益分布的曲线形状也不同。

■投资者可以无风险利率贷入或借出资金。同样，无风险证券的方差以及与其他资产间的协方差都是0。正如我们将要看到的，这个属性以无风险借贷大大地简化了均值—方差效率边界的形状。

在这些假设条件下，所有的投资者都会面对一个完全一样的效用边界。投资者间唯一不同的就是，他们必须投入的资金金额以及在投资组合均值和投资组合方差（通过平均方差无差别曲线来表示）这二者之间的个人选择。

10.1.2　机会界线

回忆一下第8章，在预期收益—标准差空间中，风险债券的均值—方差效率集一般而言都是一条曲线。曲线弯曲的程度取决于单个资产的方差以及与其他资产之间的协方差。如果有可能实现无风险借贷，那么效率集就会变成一条直线，而不再是一条曲线了。所有的有效率组合都是无风险资产和单个风险债券组合的混合体。

为了能看清楚投资者在无风险借贷时效率集会如何变化，先假设投资者只有一支风险资产可以进行投资。用A来表示这支资产，其预期收益为E（R_A），标准差为σ_A。除了证券A以外，投资者还可以无风险利率r进行借贷。那么，证券A与无风险资产的混合体将会带来的收益比率（R_p）就是：其中w_r代表投资组合中无风险资产占有的权重。期望收益可以写成：R_p的方差可以用以下公式得出：

无风险证券的方差（σ²_r）和它与证券A之间的协方差（σ_r，A）都是0。在等式的两边同时开平方，这样得出的平方根就是标准差。就得出：

因此，通过向某个资产加入一支正量的无风险资产，就可以降低资产的风险水平。加入的无风险证券占有的比例越高，投资组合的风险水平就越低。不幸的是，在我们降低一个投资组合的总体风险水平之时，也同样降低了它的预期收益水平。等式10.2和10.3可以被用来解释为什么投资组合风险与预期收益是相联系的。从公式10.3中，可以通过运算得出投入到风险债券中的资金在所有组合资金中占有的比例。这样得出：

在等式10.2中代入资产，就得到：

或者：

因此，投资组合预期收益，也就是E（R_p），是与投资组合的方差，也就是σ_ρ正相关的。此外，这种关联是线性的，因为很明显，等式10.4可以产生另一条直线。这条直线就叫做机会线（Opportunity Line）。机会线描述了通过糅合r和A得出的所有投资组合［见图10.1（a）］。向证券A中加入无风险资产可以产生出无穷多个投资组合，这些组合都在直线ra上，也就是都在机会线上。投资者可以根据个人喜好改变无风险资产在投资组合中的比重，这样一来，投资组合在这条线上与之相对应的位置也会改变。

图10.1（b）显示出，无风险资产允许投资者在一个范围内选择风险水平不同，预期收益特征各异的众多投资组合，而这些不同的预期收益特征又允许投资者达到更高的无差别曲线水平之上。没有无风险资产，只能选择证券A；有了无风险资产的加入，所有在机会线ra上的投资组合都成了可以保持的了。当加入无风险借贷这个条件时，这一点就会扩展到整条直线ra上。更有冒险精神的投资者会贷入资金，以便于在风险债券A上加大投资。更谨慎的投资者以无风险利率借出他们投资组合中大比例的资产，只向风险债券投资组合投入小比例的资金。图10.1（b）描述的就是这两类投资者，在该图示中，无差别曲线I_t表示的是谨慎的投资者，无差别曲线I_a代表有冒险精神的投资者。注意，无差别曲线表示的是以下情况：一个投资者在向其投资组合中加入无风险资产时，其投资偏好依然不变。然而，随着概率集的改变，切点也改变了［见图10.1（b）］。通过追加一支无风险资产，以上两种类型的投资者都可以达到更高的无差别曲线水平——有冒险精神的投资者通过贷入资金，谨慎的投资者通过借出资金。因而，无风险利率的可用性提高了投资者的效用水平。投资者也可以一直拒绝借贷，在这种情况下，他们就把自己的投资目标局限在证券A一支上了。然而，除非无差别曲线正好由A点切入，才能通过借贷资金达到更高的效用水平。

图10.1　一个无风险资产的投资机会

资料来源:利维:《投资学入门》第二版。

机会线有以下一些特征：

■机会线的截距是r。因此，如果一个投资者想要一个风险水平为0（σ_p＝0）的投资组合，那么这个收益就是r。要达到这个结果很简单，只要向无风险资产投入100%的组合资金，就可以了（w_r＝1），这样所有的风险就都被排除了。

■机会界线的坡度用［E（R_A）－r］/σ_A来表达，其中E（R_A）和σ_A分别是风险债券投资组合的平均收益值和标准差。很明显，预期投资组合收益率越高或者是投资组合标准差越低，机会界线的坡度就越陡。这个坡度也叫夏普比率（Sharpe Ratio），它被广泛地运用于投资组合表现评价领域中（相关内容见第22章）。

■如果用一个与σ_A相同的风险水平（σ_p＝σ_A），那么等式10.4表达的预期收益就是E（R_p）＝E（R_A）。在这种情况下，如图10.1给出，这个投资组合的均值就是E（R_A），风险是σ_A。

■通过借出（向无风险资产投资）一部分资金（也就是说0<w_r<1），并把剩余的权重，也就是（1－w_r）划分到证券A上，就可以构建一系列的投资组合。在图10.1中，这些投资组合就处在线段ra上。假设E（R_A）>r（因为投资者的风险规避），那么这样的投资组合能带来的平均收益就将少于E（R_A）。此外，标准差（1－w_r）σ_A（见等式10.3）也会小于σ_A。因此，通过持有正权重的无风险资产，我们在降低平均收益的同时也就降低了投资组合的风险水平。

■通过贷入（也就是说w_r<0，（1－w_r）>1）并且把原有的资金加上贷入的资金一道投入风险债券投资组合中，一个投资者就可以构建线段Aa上的投资组合。这就是负债投资策略。在图10.1（a）中，点A右边的部分代表了这些负债投资组合（Levered Portfolios）。负债投资组合中的部分资金是借来的，它有相对较高的收益水平和风险水平。

10.1.3　资本市场界线

在图10.1的分析中，假设只有一支风险资产，且投资者将该资产和无风险资产混合持有。在更接近于实际的场合中，存在很多风险资产，而非只有一支这样的资产。现在，分析一下投资者在这个更实际的场合中会如何选择。因此，投资者可以把每一支可选的风险资产都和这个无风险资产混合到一起构成投资组合，从而得到许多如等式10.4给出的那种直线。然而，一切有风险规避倾向的投资者，不论他们的投资偏好是什么，都会选择那个同样的投资组合，并把它和无风险资产混合到一起。他们会选择的投资组合就是那个能让等式10.4给出的那条直线产生最大坡度的组合。正如在本章中稍后部分将要看到的，这个选择很重要，因为这可以让一个投资者找到计量每一个资产风险水平的计量工具［也就是β值（beta）］，有了资产风险的计量手段，就能让一个投资者得出均衡收益率。

图10.2代表了在有很多风险证券和一支无风险资产时投资者能做出的所有选择。曲线LZ代表的是只由风险证券组成的效率边界。^[2]假设构建曲线LZ可以包括所有可能的投资组合。在曲线ALZ右边的那个小点以及标记为A和Z的那两个小点（这两个点都在直线ALZ上）代表的是单个风险证券。点A和点Z分别对应的是平均收益最低和最高的两支证券。这个曲线上所有其他的点代表的都是投资组合。正如图10.1表示的，投资者可以把图10.2中任意一资产或任意一个投资组合与一支无风险资产混合到一起，进而得出如图10.2中1号线和2号线那样的机会线。当然，问题是：哪支机会线会将投资者置于那条最高的无差别曲线上呢？

在图10.2中，直线ra的坡度最陡。一旦选择这条线，投资者就可以达到最高的可能性无差别曲线（比如说无差别曲线I₂而非无差别曲线I₁）。直线ra与曲线LZ相切。落在直线ra上的投资组合可以通过把投资组合m和无风险资产混合到一起而得到。投资组合m在机会界线的坡度最大化，通常情况下把它称为相切投资组合（Tangency Portfolio），或者是最优市场可交易性风险债券组合。不论投资者的投资偏好是什么，相切投资组合都会向所有的投资者提供其在允许借贷时能达到的最高效用水平。注意相切投资组合是一个投资组合，而不是资产，把它和无风险资产混合，最终得到的是一个风险债券投资组合和那支无风险资产的混合体。

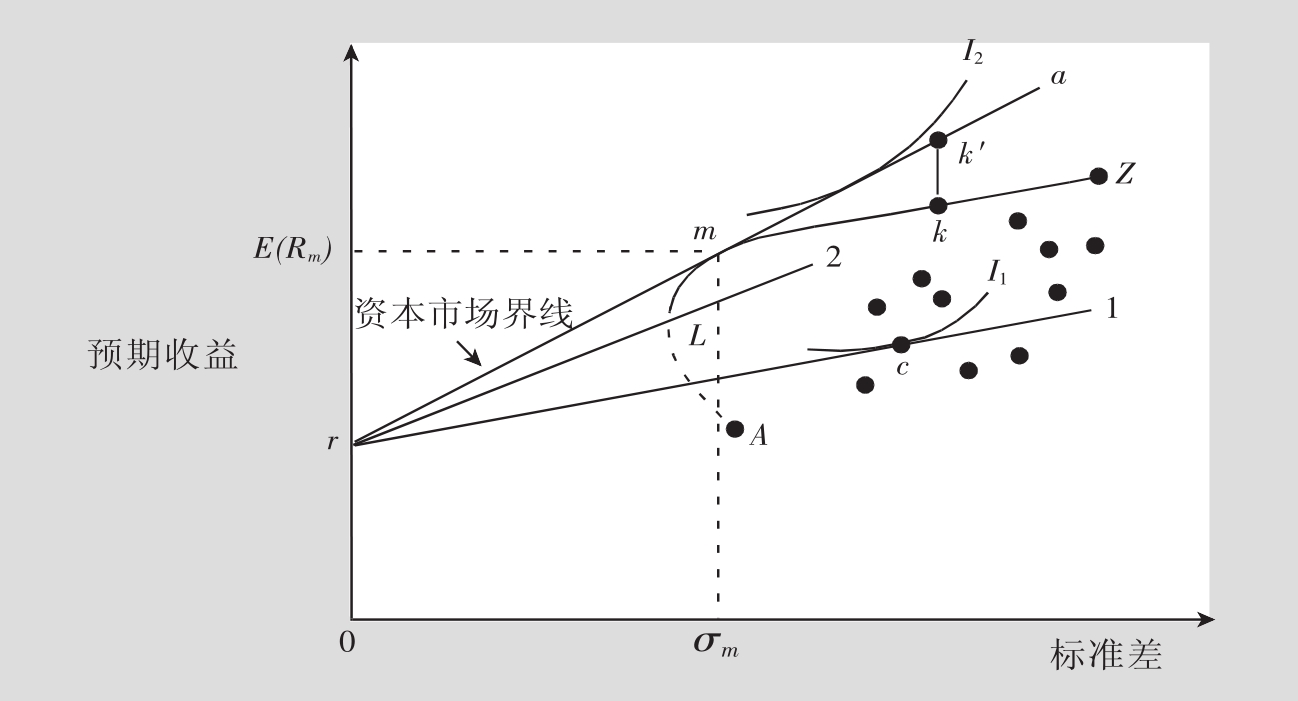
图10.2　一个无风险资产借贷的效用边界

资料来源：利维：《投资学入门》第二版。

直线ra由相切投资组合（图10.2中的m点）和无风险资产（r）间所有可能的联合形式构成。可以得出m投资组合的等式10.4来求出这条直线的平面几何公式：

这条直线称为资本市场界线（CML，Capital Market Line）。在没有借贷的情况下，均值—方差边界由曲线LZ给出（见图10.2）。如果加入借贷的可能性，那么现在这个效率边界就变成了直线ra，也就是资本市场界线了。很明显资本市场界线支配了风险债券集LZ，因为就一个在曲线LZ上投资组合而言，都可以在直线ra上找到一个更好的投资组合（除了m投资组合，因为它是曲线LZ和直线ra的交点）。比如说，直线ra上的k′投资组合就优于曲线LZ上的k投资组合，因为它在风险水平一致的情况下，有更高的收益水平。因而，一旦允许以无风险利率r借贷，利率边界就被扩展了，或者说是被改进了。同样，记住没有任何一个在直线ra上的投资组合会支配与其同在这条直线上的投资组合。因而，直线ra包括了所有有效率的投资组合。以平均方差标准（MVC）来衡量，所有资本市场界线上的投资组合都是有效率的组合，除此以外的所有其他组合（以及单个证券）都是没有效率的。

总结一下，通过把相切投资组合（m）与借贷无风险资产混合到一起得出的就叫做资本市场界线。任何像这样把m和r混合到一起的做法都会构建出一个新的投资组合，它将包含所有构成相切投资组合的风险债券。因为所有在直线ra上的投资组合都是有效率的，由等式10.5给出的线性风险—收益关系只适用于由各式各样的r和m联合体构成的有效率的投资组合。

10.1.4　投资组合分离原则

资本资产定价理论假定所有的投资者都面对相同的无风险利率以及同样的风险债券效率集。因此，所有的投资者都面对一条相同的资本市场界线。正如上面讨论的，资本市场界线产生的机会线比所有通过混合无风险资产与其他投资组合得到的直线都更陡峭。通过混合相切投资组合和无风险资产，投资者们在某一风险水平上能取得最高的可能收益。结果，所有的投资者，不论他的投资偏好是什么，都会选择资本市场界线上的投资组合，或者选择同时混合持有相切投资组合（m）和无风险资产（r）。

图10.3描述了3个潜在投资者的无差别曲线。投资者1是一个资金借出者，他/她向无风险资产投入了一定比例的资金，另外一部分则被投入到有风险的相切投资组合中。投资者3贷入资金，把他/她自己的所有资金，连同贷入的资金，都投入到投资组合m中。投资者2很明显是受了“绝不要借钱给别人，也绝不要向别人借钱”这句格言的影响：不借贷任何资金。所有3个投资者有一条共同的投资策略：都向同一个风险债券投资组合m投资。

图10.3　三个不同投资者的无差别曲线

资料来源：利维：《投资学入门》第二版。

既然所有的投资者都持有相切投资组合，那么这个组合一定和市场投资组合相等。毕竟，市场投资组合是所有个人投资者持有的投资组合之和。

以利息r借贷的可能性允许投资过程分为以下两个阶段：

第一阶段，寻找投资组合m。它位于资本市场界线和风险债券组合效率边界相切的那个切点上。既然所有的投资者都持有一个相同的投资组合，这个投资组合就应该对应于市场投资组合。因此，同样也可以根据各资产的相对市场价值来分配它们在投资组合中应占的权重，进而确定m投资组合的位置。注意，这个阶段是客观的，是每个投资者都要经历的阶段。没有必要为了确定m投资组合而去搞清每一个投资者的投资偏好（也就是它们的无差别曲线）。

第二阶段，投资者会根据自己的投资偏好，把从第一阶段得出的市场投资组合与无风险资产混合到一起，以调整这个新投资组合的风险和收益特征，最终达到最大化其效用的目的。如果想要获取比市场投资组合带来的收益多得多的盈利（通过承担比市场投资组合大的风险就可以达到这个目的），一个投资者可以贷入资金，并且把借来的资金连同他/她拥有的资金全部投入到投资组合m中。类似地，如果想把风险水平降低到市场投资组合的风险水平以下（只要接受低于市场投资组合预期收益水平的收益就可以达到这个目的），一个投资者可以把他/她的资金借出一部分，然后把剩余的部分投入投资组合m中。这个阶段是主观的，需要知道每一个投资者的投资偏好，取决于依投资者而异的无差别曲线。

把投资决策分为以上两个阶段的做法叫做分离原则。这个原则直接来源于10.1.1节所述的那些假设。具体说来，所有的投资者都面对同样的均值—方差效率边界。这个边界以一条直线体现出来，这条直线从无风险资产出发，贯穿相切投资组合（资本市场界线），且它只包含唯一一个风险资产投资组合（也就是相切投资组合）。既然每个投资者都从这个边界选择一个投资组合，每个投资者都同时持有一个相同的投资组合中的那些风险债券（也就是相切投资组合中的权重）。因此，市场投资组合作为所有单个投资组合的加权平均数，也应当与相切投资组合有相同的组成。

10.1.5　市场风险和非市场风险

回忆一下第7章，投资组合中有一种债券的风险决定于它对整个投资组合风险的贡献大小。接着，这个贡献的大小又取决于该债券的方差以及这支债券与投资组合中其他债券之间的协方差的大小。在第7章中，最优投资组合是未知的。实际上，为了描述均值方差效率集，必须考虑整个方差—协方差矩阵，然后投资者才能从均值方差效率集中选取他/她的最优投资组合（还要取决于他/她对风险和收益二者之间的个人选择）。与此不同的是，在资本资产定价模型的假设中，最优投资组合是已知的，分离原则暗示所有的投资者都持有市场投资组合。很自然地，在这个框架中，与单个资产相关的风险计量方法就是该资产对市场投资组合风险的贡献大小或者是该资产收益与市场投资组合收益之间的协方差。

市场投资组合的方差由以下公式给出（见第7章）：

在这里，w^*_i表示的是第i个资产所占的市场投资组合权重或者说是它的相对市场价值，而σ_i,s＝E（R_iR_s）－E（R_i）E（R_s）代表的是第i个资产与第s个资产间的协方差。第i支单个资产对市场投资组合方差的贡献大小取决于该资产收益与市场投资组合间的协方差：^[3]

σ_i，m=E（R_iR_m）-E（R_i）E（R_m）

既然市场投资组合是所有风险资产的混合体，也就是说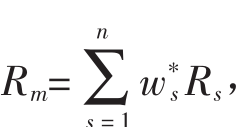：，协方差σ_i，m就准确而有效地描述了所有投资组合中资产间的协方差。具体而言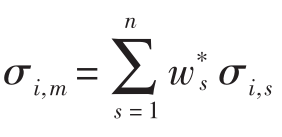，。^[4]在普遍的均值方差框架中，必须一一考虑所有单个的协方差σ_i，s。与此不同的是，在资本资产定价模型中，最优投资组合（市场投资组合）中的权重是已知的，逐一地衡量每一个单个协方差，并最终得到市场投资组合的协方差。

对于一个持有市场投资组合的投资者而言，市场投资组合的协方差是一个相关的风险计算值，因为剩下的风险都通过投资组合多样化而被消除了。而且，投资者需要因为承担系统性风险而不是非系统风险而得到补偿。稍后还要讨论这个问题，在这里要介绍一下市场间协方差的标准化版本。

在实际生活中，市场的协方差一般都会除以市场投资组合的方差，以达到标准化的目的。

这个值就叫做市场β值（Market Beta）。市场β值测量的是资产与市场投资组合相对的（系统）风险。市场投资组合的β值又是什么呢？回忆一下第7章，投资组合中一支证券与其自身的协方差就是它的方差。因而，市场投资组合的β值就是1，因为：

因而，如果β_i>1，那么该资产就有比市场更高的（系统）风险水平。这样的证券一般称作旺盛资产（Aggressive Assets）。比如说工业技术股票就倾向于有较高的β值，很多工业技术基金的β值都是2.0，甚至更多。相似地，防御资产（Defensive Assets）的（系统）风险水平就低于市场的风险水平（β<1），而中性资产（Neutral Assets）的市场β值则为1。_i

除了计量相对风险，市场同样也测量资产对市场运动的敏感度。记住β_i仅仅是下列公式给出的回归线坡度：^[5]

在这里，α_i是回归线的截距，或者说是该资产的“阿尔法”，e_i是对回归线的偏离程度，称为误差项（Error Term）。这个误差项是一个随机变量，其均值E（e）_i＝0，方差是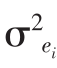。^[6]描述R_i和R_m之间关系的回归线被称为特征线（Characteristic Line）。^[7]这条回归线用的是无风险利率盈余收益（Returns in Excess of the Riskless Rate），或者说就是盈余收益（Excess Returns）。这并不影响β值的定义，然而，的确会影响到对α值的界定。使用盈余收益的原因稍后就会明白，那时，α值将会被解读为“定价误差”。^[8]

图10.4　特征线示例

因此，β值计量的是第i个资产或投资组合收益率对市场投资组合收益率变动的敏感度。β值越大，对市场的变动就越敏感，对持有市场投资组合的投资者也就越有风险。比如说，如果β_i＝2（旺盛资产），且市场收益率增加1%，那么该资产的预期收益率平均会上扬2%。然而，如果市场收益率下跌了1%，该资产的收益率预计就会下跌2%。该资产波动的幅度是市场投资组合波动幅度的2倍。相似地，如果β_i＝0.5（防御资产），那么该资产的波动幅度就只有市场投资组合波动幅度的一半了，相对而言就是比较安全的。防御资产帮投资者避开巨大的损失，但同时也不允许投资者获得高水平的预期收益。最后，中性资产（β_i＝1）一般来说与市场的走势完全一致。

图10.4描述了与旺盛资产以及中性资产相对应的特征线。计算机公司的股票，比如说Apple电脑公司和Microsoft公司的股票，都可以看做是旺盛资产。当市场上扬x%时，它们上扬的幅度通常会大于x%；当市场下跌x%时，它们下跌的幅度通常也会大于x%。公用事业公司的股票，比如说佛罗里达天然气公司和佛罗里达电力电气公司的股票，则可以看做是防御资产。当市场上扬x%时，对天然气或电力的需求量就会上升，但是升幅不大。当市场下跌x%时，对天然气或电力的需求量也下跌，但是跌幅没有其他产品总体的跌幅那么大，所以，这些公司的股票在市场下跌x%时，下跌的幅度会小于x%。

有趣的是，一个投资组合的β值仅仅就是其中各单一证券β值的加权平均数，如果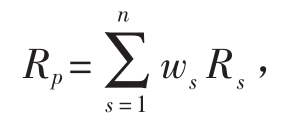那么：^[9]

β值允许同一种有用的方法来解构资产（或证券投资组合）的方差。特别是R_i的方差可以解构成：^[10]

因而，方差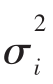可以被分解成两项。第一项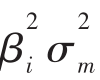是该公司的系统风险（Systematic Risk），或者说市场风险（Market Risk），代表的是来源于整体市场波动性的那部分风险。第二项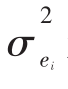是该公司的非系统风险（Unsystematic Risk）成分，或者说非市场风险（Non-market Risk），代表的是来源于整体市场波动性以外的那部分风险。非系统风险和公司的具体波动性相联系。如果一个资产的价格波动和市场运动相联系，那么该资产的误差项就是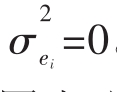。与公司相关的具体因素越多，误差项的值就越大，因为误差项计量的是回归线周围点群的离散程度。

如果在等式10.8的两边同时除以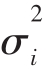，就能得出下列等式：

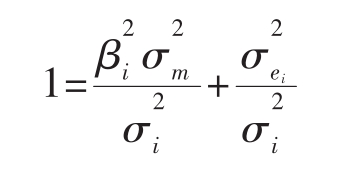
其中，第一项是一个资产（Proportion）系统风险在总体风险中所占的比例，第二项是非系统风险所占的比例。

表10.5表示的是把5支证券的方差分解成系统和非系统风险的情况，此处所用的数据是在20多年的时间里按月收集的。注意道琼斯工业股指的β系数是1.17，CWE的β系数是0.55。该表也表明了系统和非系统风险的比例（此处，当然这两个部分之和为1）。像CWE那样的专业电力公司（本身就是高度制度化的）有较低的非系统风险。然而，GE公司是一个多样化的大公司，对市场的变化情况很敏感，因而有较高比例的系统风险。

表10.5　月度方差分解（市场标准差为0.047）

在表10.5中，GE公司股票的标准差是0.067，CWE公司股票的标准差则是0.055。因此，就总体风险水平而言，GE公司的股票风险水平更高。然而，该公司股票标准差的误差项（0.041）比CWE公司股票的（0.049）要低。因而，CWE公司股票中可以通过投资组合多样化去除的风险在总体风险水平中占有的比例，要高于GE公司股票能通过投资组合多样化来消除的风险在总体风险中所占的比例。

10.1.6　证券市场界线

正如上面讨论的，在资本资产定价模型的假设中，所有的投资者都持有市场投资组合。此外，对持有市场投资组合的投资者而言，资产的相关风险就是市场风险，这个风险用市场β值来衡量（其本身是市场协方差的标准化版本）。剩余的非市场风险没有关系，因为它可以通过投资组合多样化来消除。与此相联系的是，一个投资者因为承担了系统风险（而不是非系统风险）而得到补偿，这个补偿的具体形式就是α值高于无风险利率的风险酬金。再具体点说，在资本资产定价模型的假设中，下列线性风险—收益关系应该是成立的：

这个线性关系称作证券市场界线（SML，Security Market Line）。^[11]证券市场界线断言：证券i的预期收益率等于无风险利率加上风险酬金[E（R_i）-r]，也就是投资者要求获得的比投资无风险资产带来的更高的预期收益[E（R_m）-r]。这个风险酬金等于市场风险酬金乘以该资产的β值。^[12]既然，[E（R_m）-r]＞0（假设投资者会进行风险规避并因而要求正量的风险酬金），就可以得出β_i值越高，风险就越大，而风险酬金也就越多。回忆一下，β_i只反映市场风险，只有该公司方差中的系统性部分才与风险酬金，进而与预期收益率的决定有关。与此不同的是，资本资产定价模型并不能解释非系统风险，这种风险可以通过持有市场投资组合来消除。

我们强调，证券市场界线是从以下事实中直接得出的：市场投资组合是位于效率边界上的。为了让市场投资组合有平均方差效率，单个资产都应该落在证券市场界线上，相似地，如果至少有一个资产位于证券市场界线的上方或者下方，那么该市场就是没有效率的。换言之，证券市场界线是市场投资组合效率性的充要条件。附录10给出了以上这个论断的公式化证明。我们已经讨论过了这些证明背后的经济直觉。在市场均衡的条件下，所有的投资者都持有市场投资组合，因而投资者会因为承担市场风险（以β值衡量）而要求得到风险酬金，但是非市场风险却没有酬金（因为这种风险已通过投资组合多样化而被消除了）。

记住证券市场界线可以用特征线（等式10.7）来表达。具体说，减去该等式两边的预期并让E（e_i）＝0，我们就可以得到：

E（R_i）-r=α_i+β_i[E（R_m）-r]

接着，把E（R_i）代入等式10.9，得出：

[E（R_m）-r]β_i=α_i+β_i[E（R_m）-r]

或者：

α_i=E（R_i）-r-[E（R_m）-r]β_i

总结一下，在某资产β值一定的情况下，α值（Alpha）计量的是此资产期望收益E（R_i）与均衡收益率之间的差异。因此，α值计量了高于资本资产定价模型预测的预期收益率（或者说正常收益r+[E（R_m）-r]β_i的异常收益（Abnormal Return），也就是定价误差（Pricing Error）。证券市场界线暗示，落在其上面的所有投资组合的α值都应该为0：

如果有一资产的α′_i值大于0，那么该资产就应该位于证券市场界线之上，而且其估量误差应该为正数。换句话说，对该资产的估计低于其实际的价格，其预期收益水平太高了，价格应该上升些。与此相反的是，如果α′_i值小于0，那么该资产就应该位于证券市场界线的下方，它的价格被高估了。

图10.6表示的是证券市场界线，如果β_i＝0，那么就可以得到E（R_i）＝r。因而，正如预料的一样，对于无系统风险的资产，其收益水平应等于无风险联系r。如果β_i＝1，那么可以得出E（R_i）＝E（R_m）。这时，这一资产的价格一般会随着市场的波动而一前一后地波动。因此，该资产的风险水平与市场风险一样大，所以一般而言，其收益水平就应该等于市场投资组合的收益率水平。当β_i>1时，这一资产就是旺盛资产，也就是说它比市场投资组合有更高的系统风险水平。因此，在市场平衡的状态下，旺盛资产就有一个标志性特征，就是它有比市场预期收益水平高的预期收益水平。如果资产是防御型的，那么它的预期收益将少于市场投资组合的预期收益。注意，图10.6并没有表示出β值小于0的资产将会有什么样的预期收益。这样的资产很少有，很多资产都会与市场正相关。然而，我们还是可以通过卖空或运用其他衍生金融工具（比如说出卖期货契约）来得到负的β值。证券市场界线暗示，负β值的证券能带来的预期收益率比无风险利率r低，因为［E（R_m）－r］>0，这个结果甚至还可能是负数。这样说有什么意义呢？当然，如果一个风险投资组合的收益率低于无风险利率r，持有一个有负β值的投资组合就毫无意义。然而，向投资组合中加入一支负β值的证券却是有意义的，因为这样的资产可以稳定整个投资组合的收益（也就是说可以降低投资组合的风险），并且投资者会因此而接受一个相对较低的收益。因此，证券市场界线同样适用于β值为负的情况。

图10.6　安全线（SML）

资料来源:利维：《投资学入门》第二版。

证券市场界线代表的是市场平衡状态，在这种状态下，所有的投资者都持有他们的最优投资组合，因而没有理由提供也不需要买入资产。如果一些资产偏离了证券市场界线，那么市场就处于不均衡的状态。比如说，在图10.6中，A证券处在证券市场界线的下方，也就是说它的收益率相对于它的β值而言太低了，与此同时，资产的预期收益又太高了。各资产与证券市场界线之间的垂直距离描述的是该资产的α值，也就是定价偏误。定价偏误是平衡收益率与实际预期收益率之间的差异。在这种情况下，投资者可以通过卖出A证券（其α值为负数，也就是说定价过高），买进B证券（其α值为正数，也就是说定价过低）来改善他们投资组合的风险—收益特征。通过卖出A证券，投资者会降低A证券的价格，并提高其预期收益水平。而通过卖出B证券，投资者则会抬高B证券的价格，并且同时会降低B证券的预期收益水平。这种买进和卖出会一直持续到进一步的交易已经不能改善投资者的投资组合风险—收益特征为止。这时，所有的证券都会落到证券市场界线之上，α值为0，市场处于平衡状态。

10.1.7证券市场界线和资本市场界线之间的联系

证券市场界线描述了均值和β值之间的关系，它可以适用于所有的资产以及一切投资组合，而不论这些组合是否是有效率的。相反，资本市场界线描述的是均值与标准差之间的关系，适用于有效率的投资组合。资本市场界线不适用于无效率的资产和投资组合，因为投资者不会要求获得非系统风险补偿。为了便于理解这一点，把公式10.8重写成下列等式是很有用的：

将这个等式代入证券市场界线的表达式（等式10.9）得出：

有效率的投资组合没有非系统风险，也就是：

因此，上面的这个等式就化简为资本市场界线（CML）的表达式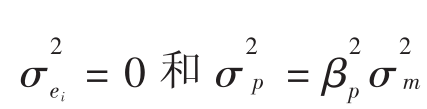：。总结一下，一个有效率的投资组合中包括系统风险，也就是：σ2＞0。因此，我们可以用β值（证券市场界线）、方差或者标准差（资本市场界线）来描述风险。然而，这不适用于无效率投资组合，只适用于证券市场界线。

图10.7表示的是资本市场界线。注意其坡度是：[E（R_m）-r]/σ_m，而证券市场界线的坡度是E（R_m）-r。如果向一个标准差为σ_m的有效率的投资组合（市场投资组合）投资，通过运用资本市场界线，就得到一个预期收益E（R_m）。这一点与证券市场界线是一致的，因为市场投资组合的β_m＝1，预期收益是E（R_m）。同样，因为所有的投资组合和资本市场界线都仅仅是m与无风险资产的混合体，一个投资者在增加投入投资组合m的资金比重时，也同样会提高β值。^[13]

为了能与本章中稍前的图10.6相互联结，图10.7中依然包括有证券A和证券B。记住，在市场均衡的状态下，2支证券（证券A′和证券B′）都会位于资本市场界线的下方。表面上，这两支证券都是有效率的。这2支证券到资本市场界线的水平距离（A′A″和B′B″）计量的是这2支证券的非系统性风险。要强调的是：这种对资本市场界线的偏离并不是暗示——市场正处于不平衡状态。这仅仅意味着这两支证券是没有效率的，投资者不应该单独持有它们。尽管如此，投资者应该在投资组合中给这些证券分配与其市场价值相适应的权重。为了检验市场是否正处于不平衡的状态，要看是不是所有的证券都落在证券市场界线之上。当然，在市场平衡的状态下，证券不会位于资本市场界线以上的地方。比如说，在图10.7中，证券B就位于资本市场界线以上的地方。这意味着投资者可以通过买入证券B，来改善他们投资组合的风险——收益特征。一旦买入证券B，投资者将会在提升证券B的价格的同时降低其预期收益水平。在市场均衡时，证券B′位于证券市场界线之上，资本市场界线的下方。

图10.7　资本市场界线（CML）

10.1.8　以历史数据评估特征线

回忆一下10.1.5节：β值表示的就是特征线的坡度，

R_i-r=α_i+β_i[R_m-r]+e_i

此处，α_i是回归线的截距，e_t表示的是一个与公司相关的因素，其均值为E（e）_i=0，方差是σ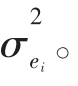在实际生活中，α_i与β_i这两个系数都是未知的，因为不知道未来的收益分布。然而，我们一般都会知道单个证券的T形历史收益（一个时间序列数据集）样本。比如说，对每个证券来说，我们可以通过总共120次的观测，来获得1993年1月～2002年12月之间的月度收益样本。在全书中，将以R_i，t来表示第i个证券在t时期内的收益，同一时期的市场组合收益以R_m，t来表示，以r_t来表示无风险证券的收益。这样的数据允许以回归分析（Regression Analysis）来评估特征线。回归分析这一统计工具在本书末尾的附录A中将有详细的介绍。这个统计工具在许多统计软件包和空白表格程序里都有，甚至更为先进些的口袋计算器里也包含有统计工具。

粗略地说，用回归分析来衡量特征线，就是要找出一个能从统计的角度描述R_i，t和R_m，t之间关系的评估指数。学术界现在有好几种不同的回归方法，哪一个才是最佳的拟合，要取决于观测的统计学分布。一个最常见的假设就是：真正的（未知的）收益分布（截距α_i，β值β_i，以及非市场性风险）不会随着时间的改变而改变，以至于所有的观测都遵循同样的一根特征线，也就是说：

R_i，t-r_t=α_i+β_i[R_m，t-r_t]+e_i，t

附录A更详细地介绍了如何计算标准误差以及R平方。通过用（R_i，t－r_t）来代换y_i，用（R_m，t－r_t）来代换x_1，i，就可以得出适合评估第i个证券特征线的统计数据。比如说，估算的β值由以下公式得出：

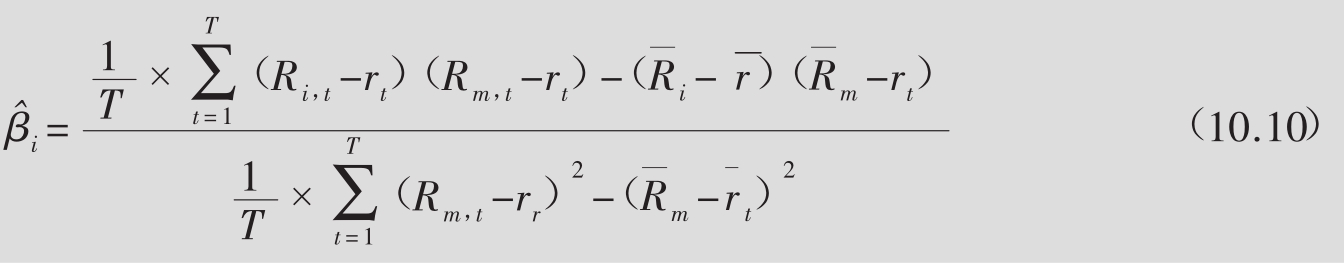
此公式中，r代表的是作为样本的那个时期里的平均无风险比率。类似地，估算的α值可以从以下公式中得出：

附录A说明的是如何用月度盈余收益计算Microsoft公司股票的各种相关统计数据。这个计算中的数据是在1991年1月～2000年12月这一时期，通过120个月的观测得来的。图10.8总结了这些计算结果。这个图是一个散射图，比较了Microsoft公司股票收益和CRSP全股指数的收益。CRSP是所有在纽约证券交易所、美国证券交易所以及纳斯达克交易的股票的价值加权平均数。同样，图10.8包含了估算的回归线，或者说是最佳拟合线。评估指数、标准误差和R平方在右下方的角落里给出。这时，估算的α值为1.248%（一个正量的异常收益），估算的β值为1.535（说明是旺盛资产）。不幸的是，这些估值非常不准确，这一点可以从标准误差值（括号里的数值）看出：两个值的标准误差都很高（分别是0.877和0.216）。附录A显示，可以用95%的无置信区间来说，Microsoft公司股票真正的α值在-0.506～3.002（1.248±2×0.877）之间，这是一个很宽的区间了。相似地，β值的95%无置信区间在1.103～1.967（1.535±2×0.216）之间。正如在附录A中讨论到的，在评估资产的特征线时，有这个程度的不准确性是典型的。问题是，单个资产收益在很大程度上取决于与资产有关的因素，而这些因素使衡量该资产对于市场风险的贡献变得困难了。比如说，Microsoft公司股票的R平方是0.299，这个数据意味着只有30%的收益波动可以归因为市场收益的波动；剩余的70%全都要归因为非市场性因素的作用。对投资组合而言，问题一般都没有那么严重，因为单支资产与具体资产相关的收益抵消了投资组合环境的影响。

图10.8　估算Microsoft公司股票的特征线

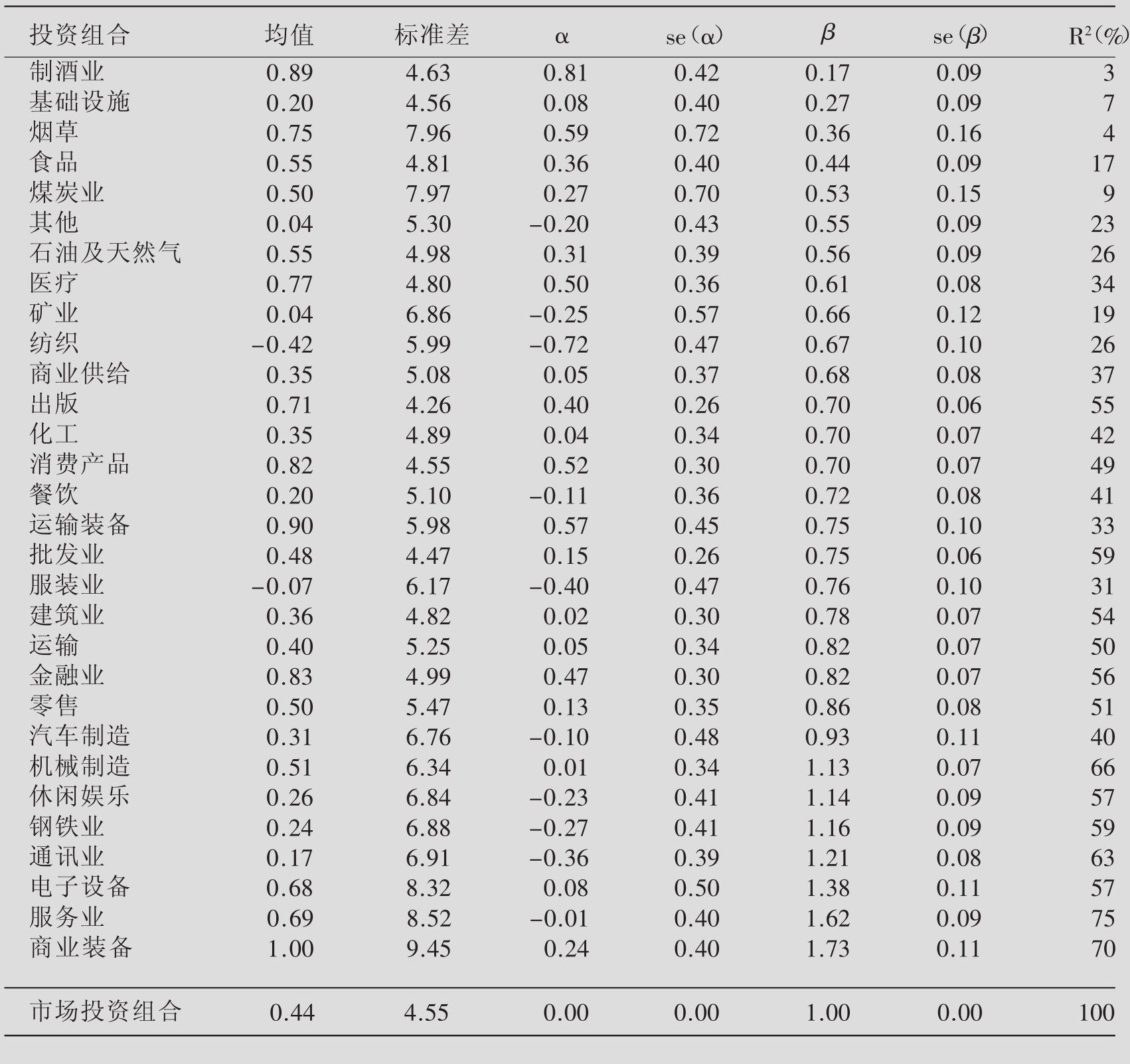
图10.9包含了30个工业投资组合在1993年1月～2002年12月这120个月里的α值和β值。^[14]这个图同样包括了那些系数的标准误差和R平方。那些结果以β值的大小排列。β值最高的工业部门是商业装备业，β值最低的工业部门是啤酒和白酒制造业。留意烟酒工业的良好表现。在20世纪90年代中，这两个工业有很高的风险调整收益，这一点可以从α值看出来：分别是0.81和0.59。

以历史数据来评估特征线也会受到限制。α值和β值可以随时间的推移而变化。比如说，一家公司股票的α值会升高，如果该公司开始向比现在正在投资的项目风险更大的项目投资，或者如果该公司发布新的债务声明（这对资产声明是很重要的）。甚至对于整个产业而言，以上论断也是适用的。比如说，工业技术产业在近年来已经变得难以辨认了：出现了崭新的工业，各公司在其发展的更早阶段（也更危险）阶段就进入了公共市场。因为有这些原因，业内人士经常建议不要用近10年以前的数据来评估特征线。同样的，正如在《理论联系实际10.1》中解释的，只有把历史收益的相关理论与自己的判断结合起来，才可以得出最好的评估。

表10.9　各行业的β值

10.1.9　资本资产定价模型的理论扩充

在10.1.1节，归纳了资本资产定价模型最重要的一些理论假设。通过放宽这些假设条件，得出了对资本资产定价模型的各种概括性模型：零β模型、一般资本资产定价模型、多时间段资本资产定价模型和基于消费的资本资产定价模型。本书不会涉及关于这些模型的详细讨论，有兴趣的读者可以参阅本章末尾提到的那些相关书目。

这些概括性模型放松了关于以无风险利率借贷资金可能性的各种假设。它们不处理有关卖空的假设。注意10.1.1节没有提到任何有关卖空的假设。然而，该节中的例子已经含蓄地暗示了如下假设：卖空行为是不允许的。有趣的是，卖空限制并没有影响资本资产定价模型。回忆一下，在资本资产定价模型中，所有的投资者都持有市场投资组合，并且市场投资组合根据其中各资产的相对市场价值向各资产分配组合权重，而相对市场价值总是为正的。因此，没有投资者会卖空证券，就算他们被允许这样做。换句话说，卖空限制不是约束性的。

零β模型

资本资产定价模型假设投资者能以无风险利率借贷资金。正如10.1.3节讨论过的，这个假设暗示了如下事实：在平均标准差空间中，均值—方差效率集是一条直线。与此相联系的是，所有的投资者都会持有相同的风险债券投资组合（也就是市场投资组合）。在实际生活中，投资者的确可以通过购买政府国债来以无风险利息借出资金，只要他们购买的政府国债的到期日与他们投资的时间跨度的最后一天一致就可以了。然而，投资者一般不能以无风险利息贷入资金。比如说，投资者们如果要向银行贷的一笔无保险贷款（没有担保的贷款），他们一般会向银行支付高于无风险利息的酬金率，以补偿银行承担的信用风险。因此，投资者一般都只能以无风险利率借出资金，而不能以无风险利率贷入资金。由布莱克（Black，1972）构建的零β模型就是以这个事实为基础的。

在零β模型（Zero-beta Model）中，效率集不再是一条直线。相反，它由以下两个成分构成：一是从无风险资产到相切投资组合之间的线段；二是自相切投资组合开始的一条曲线。这意味着不同的投资者一般不会持有相同的风险债券组合（市场投资组合）；资本资产定价模型中两基金分离原则在这里不再适用了，所有的投资者都会联合持有无风险资产、相切投资组合和市场投资组合。然而，所有的投资者都会选择持有一个有效率的投资组合，没有投资者会选择持有一支其均值和方差被支配的投资组合。

有趣的是，如果所有的投资者都持有一个有效率的投资组合，那么市场投资组合——其本身就是市场中所有单个投资组合的加权平均数——也是有效率的。^[15]类比附录10中的分析，投资组合最优化的最优条件中暗示：在市场平衡的条件下，资产的预期收益率和市场β值之间有一种线性关系。此处的市场β值类似于等式10.9中的证券市场界线。尽管如此，与最初的资本资产定价模型相反，截距或者零β值比率可能会超过无风险利率r，坡度或者β值风险酬金可能会比证券酬金少。

一般资本资产定价模型

资本资产定价模型没有考虑交易成本的问题。一般而言，买进股票的数量越多，交易成本在交易额中所占的百分比就越低。投资者，特别是小投资者，在他们的投资组合中只持有数量较少的股票，因而并不向市场投资组合投资。在最优组合中只有少量股票的情况下，为了解释资产的定价问题，利维（Levy，1978），马科维兹（Markowitz，1990），默顿（Merton，1987）和夏普（Sharpe，1991）提出了一个与资本资产定价模型相似的模型，但是在这个模型中投资者却被允许只在投资组合中持有相对较少的资产。这个模型就称为一般资本资产定价模型（GCAPM，General Capital Asset-pricing Model），说它是“一般的”，是因为一旦交易成本从这个模型里被排除出去而不再考虑，资本资产定价模型就成了GCAPM的一个特例了。在这个模型中，所有的投资者都持有不同的投资组合，因此每个投资组合也就都有一个不同的β值（这个β值是与所持有的投资组合相逆）。第i个资产的β值就是所有这些β值的加权平均数，而这些β值取决于不同投资者向资产中投入的资金多少。^[16]

多时间段资本资产定价模型

资本资产定价模型是一个单时间段模型，也就是说它假设投资者们在某时间段开始时选择了某个投资组合以后，就等着时间慢慢过去，不确定性变小，最后在该时间段的末尾结清该投资组合。现实生活中，很多投资者的这一问题可以用一个多元模型来更好地描述，在这个模型里，收益分布（均值、方差和标准差）以及由此而来的均值—方差效率边界会随着时间的推移而改变，而投资者也会相应的对投资组合作出修正。默顿（Merton，1973）提出的多时间段资本资产定价模型（ICAPM，lntertemporal Capital Asset-pricing Model）就是用多维视角来描述这种金融市场平衡的。默顿基本上提出了以下三个问题：投资者如何在有时间段的一开始就选择一个投资组合，以便这个投资组合不仅在某段时期内是最优的，而且在该投资者整个的投资时间跨度里也是最优的呢？用学术性的话来说，就是投资者如何确定一支动态性最优投资组合？ICAPM的宗旨就是：最开始选择的投资组合不仅要处于效用边界上，而且这种最优性还要能保证不被未来投资机会集中那些不如意的变化（比如说利率和风险酬金水平下跌，或者方差和协方差增大）所影响。对单个产权而言，这个理论的暗示就是资产是带有两种风险酬金的。第一种风险酬金，是投资者因承担市场投资组合价值在各个时期内波动的风险，而得到的补偿。这和资本资产定价模型中的β酬金很相似。第二种酬金补偿了投资者承担的效率边界恶化风险。如果某资产在投资机会集中发生不好变化的情况时仍然趋向于获得高收益，那么投资者们就会想要持有该资产，并把它当作一种保障。这种需求上的增长可能会导致该资产更高的平衡价格（在其他情况相同时）。ICAPM的一个主要思想就是要在定价等式中反映这种保障需求。

ICAPM可以被视为是对资本资产定价模型的概括。因为如果投资者都是单期投资者，且不会在效率边界发生变化时修正他们的投资组合，或者如果收益分布和效率边界不会随着时间的变化而变化，资本资产定价模型就成了ICAPM的一个特例了。^[17]

基于消费的资本资产定价模型

资本资产定价模型假定投资者的预期效用可以用他们投资组合收益的均值与方差来公式化。在现实生活中，投资者一般都不是从投资中直接获得满足感，而是从当时或未来的商品以及服务的消费中获得这种满足感（相关内容见第7章）。当然，一个金融投资组合可能会是支持将来消费的资金来源之一，因此投资者可以间接地从投资组合的收益中获得满足感。但是，因为种种原因，我们不能简单地把投资组合与消费等同起来。除了投资组合的收益，投资者还有其他的消费资金来源，如人力资本和私有财产。同样，消费者的生活计划不会只局限于某一时期内遭受的亏损，无论那个亏损的灾难性有多大，也不意味着消费就会马上随着被调整，以适应这种灾难性损失带来的影响。比如说，对股民而言，1987年10月是近代历史上最为糟糕的一个月。然而，股市下跌对于消费的影响从总体上来说，小得惊人。与此相对照的是，20世纪70年代持续的熊市的确曾经对消费有过重大的影响，尽管这个时期的月度收益损失并没有1987年10月的损失那么有灾难性。因此，只看股票收益可能会对涉及投资的消费风险产生错误的印象。在布瑞顿（Breeden，1979）提出的基于消费的资本资产定价模型（CCAPM，Consumptionbased Capital Asset-pricing Model）中，证券酬金是和单个β值成比例的，这个β值是与人均消费增长而非市场投资组合收益之间的协方差。在这个模型中，如果某资产在消费降低的同时，收益也变少了，那么该资产就更有风险。有风险规避倾向的投资者会选择预期收益最高的资产，而这个预期收益是用投资者在其他附加基金中的收益值来衡量的。这个模型直接构建于以下一些直觉之上：在总体消费水平很低的时候，每多1美元所能满足的消费需求在消费者的眼中，都会多于那1美元的实际价值。而当市场行情很好的时候，很多人都有能力维持舒适的生活水平，此时每多1美元所能满足的消费，就不会让一个人觉得，会使他自己的生活水平得到多大的改善。但是，在市场环境不好的时候，能多出几美元来满足商品消费需求则是一件令人高兴的事情。基于这个递减的边际消费效用，在总体消费水平较低的时候，有高收益的证券就会受到股民的青睐，进而抬高其价格（与此同时降低其预期效用水平）。与此相对照的是，与总体消费水平同步正向变化的股票则会要求有更高的预期收益，因为它们在高收益最没有价值的经济形势之下仍然可以带来较高的收益。

如果人均消费增长等于市场投资组合的收益，标准的资本资产定价模型就成了CCAPM的一个特例。^[18]

三矩资本资产定价模型

资本资产定价模型是基于均值—方差框架的定价模型。在均值—方差框架中，投资者的预期效用会随着预期收益的增长而增长，随着市场投资组合方差的降低而降低。均值和方差以外的矩，比如说偏度，被假定为是和投资者不相关的。然而，既然金融资产在收益分布中表现出了非对称性和函数图像的“肥尾”（参见第8章），对更高的矩的偏好也许会变得相关。在其他条件相当的情况下，投资者一般喜欢正偏度（大额盈利的几率高于等额亏损的几率），而不喜欢负偏度（大额盈利的几率小于等额亏损的几率）。比如说，彩票之所以有人买，就是因为它的收益形式有正偏度。克劳斯和立曾博格（Kraus和Litzenberger，1976）把以均值方差框架为基础的资本资产定价模型扩展成了一个，三矩或均值—方差—偏度资本资产定价模型（3M CAPM，Three-moment or Mean-variance-skewness Capital Asset-pricing Model）。在这个框架中，选择1只股票要以其均值、协方差和共偏度（也就是该股票对市场投资组合偏度的影响）为基础来考虑。在标准的资本资产定价模型中，1只股票的价格取决于该股票对市场投资组合风险的影响。而在现在这个模型里，这个风险就取决于方差和偏度了。在这个框架中，具有较高的负共偏度值的股票会没那么有吸引力，因而会有较高的预期收益水平。比如说，小股票偏向于有较高的负共偏度值，这使得它们拥有比相等协方差计量出的更高的风险水平（哈维和西迪克，2000）。以偏度为基础的预期风险调整可能会帮助我们解释为什么这些股票在历史上会有较高的收益水平。如果股票收益呈正态分布，或者如果投资者不关心偏度值的大小，资本资产定价模型就成了3M资本资产定价模型的一个特例。

理论联系实际10.1

FT

评估预期收益的模型博弈理论是好的

金融理论说，风险水平较高的资产一定会带来高水平的预期收益，资产定价模型就是用来量化这种风险和预期收益之间的关系的。资本资产定价模型（CAPM）说，一种资产的风险水平越高，它的价格在总体上就会越紧密地随着市场中其他股票的价格而波动。因此，衡量一支股票风险的适当方法就是计量这支股票与整个市场的联动程度，这个程度可以用一个称为β值的计量工具来描述。某支股票的预期收益E（r）与该股票的β值之间有线性的关系。具体而言，股票预期收益超过无风险利率的那部分（预期盈余收益）可以用下列等式来表达：E（r）-rf=b×E（rm－rf）。在这个等式中，E（rm－rf）的比例是恒定不变的，它描述的是相对于总体市场而言的预期盈余收益。这个收益常常被称作资产酬金。选择多高的无风险利率取决于我们的预期目标。为了预测下个月的股票预期收益，与此目的相适应的无风险利率就应该是一个月就可以到期的T券的收益率。如果想要估算一个公司的资本成本以判断该公司进一步可能会有的现金流价值，无风险利率就应该选择到期时间更晚的T券所能带来的收益率。这支国债到期以前的时间跨度应该接近于该公司现金流的时间跨度。应当避免把长期国库券的收益率作为无风险利率，因为这些国库券的收益率可能同样会反映其他与风险——比如说通货膨胀风险——相关的酬金。

上面的等式解决所有的问题了吗？不全如此。等式左边的各项，也就是β值和资产酬金，都是需要估算的。β值的估算法，通常是通过将股票的月收益回归到最近5～10年的市场收益上来估算的。比如说，如果用1996年1月～2000年12月之间的数据来估算GM公司股票的β值，其结果就是1.11。要用多少数据来估算β值呢？这里牵涉的取舍与样本均值里涉及的很相似：用的历史数据越多，估算也就会越准确，但是引入旧数据带来的偏差和几率也就会越大。与样本平均数不一样的是，这里使用的数据如果是通过更加频繁的观测得到的，那么估算值的准确度就会有所提高。比如说，如果以月度数据为基础来估算该公司股票的β值，其95%的置信区间就是0.65～1.57之间。然而，如果用以周为单位得出的数据来估算这个值，其95%的置信区间的范围就更窄了，为0.69～1.08之间。用这种数据得出的β值为0.88。然而，只有对流动性和波动性水平都最高的股票，我们推荐用以周为单位得出的数据来代替月度数据的方法，来提高β值估算的准确度。对于其他股票而言，一周的价格变动只是买卖差价围绕着真实价格的上下波动而已，这种情况会带来附加的估算误差。同样，整个市场的行情信息也许要花费一些时间才可以影响到清偿股票的价格，因为一般的β值估算方法都会低估清偿股票的β值。传统上，由麦荣·斯格内斯（Myron Scholes）和约瑟夫·威廉斯（Joseph Williams）提出的一套估算方法就可以被用来估算清偿股票的β值。

从以上GM公司股票的例子中就可以看出，β值的估算有很大的误差。要降低这些误差，一个很有用的方法就是把通常的估算结果“缩小”到一个合理的值，比如说是1。这个数值之所以是合理的，是因为所有股票的平均β值都是1。这个缩小的β估算值是平常样本估值和被缩小的那个值的加权平均数。比如说，在Merrill Lynch公司发布的“调整后”的β值中，有2/3的权重分配给了样本估算，1/3的权重分配给了估算值是1的估算方法。因此该公司股票调整后的β估算值就是：（2/3）×0.88＋（1/3）×1＝0.92。有理由说，把缩小后的β值当作“贝氏评估指数”是不错的，该评估指数以18世纪英国数学家托马斯·贝叶斯（Thomas Bayes）的名字命名。这样得出的β值不仅反映数据，也反映了先验的知识，即判断。和其他许多统计学者运用的评估指数不同，贝氏指数在统计学和决策理论方面都有稳固的理论基础。在评估GM公司的股票以前，我们知道它是1只股票，因此，根据先验的知识，可以猜测到一个较好的β值为1。同样，我们还知道该公司更多的情况，比如说，知道这个公司属于哪一个工业门类。既然汽车制造企业股票的平均β值约为1.2，那么可以合理地依据先验知识，把它的股票的β值猜测为1.2。应该向猜测值分配多少权重，以及应该向估算值分配多少权重，取决于样本评估的精确度以及对先验知识的信任程度。这种信任，举个例子来说，可以建立在汽车制造商β值离散程度这一基础之上：这些企业股票的β值越是集中在1.2附近，就给依靠先验知识得出的猜测值分配越大的权重。如果向依据先验知识得出的结论和每周的数据为基础得出的估算值分配相同的权重，它的β值经过工业门类调整后就是：（1/2）×0.88＋（1/2）×1.2＝1.04。

不幸的是，资本资产定价模型没有涉及预期市场收益的算法，而估算资产酬金比估算β值可又要难得多了。时间间隔更短的数据也无法帮助我们估算这个值，同时也没有什么先验知识可以依据，进而得出一个猜测值。最常用的方法就是求出很长的一系列盈利市场收益的平均数，这个方法得出来的资产酬金是每年5%～9%，具体的酬金率取决于作为样本的时期有多长。最近，罗伯特·斯坦博（Robert Stambaugh）做了一项关于资产酬金率的研究。作者在该研究中，把美国现在的资产酬金率定为每年4.8%。这一估算结果的依据是一个考虑过去165年间资产酬金率变化的模型。把这个公司结果和GM公司股票的工业门类调整后的β值以及6%的无风险利率放到一起考虑，资本资产定价模型该公司股票的年预期收益（其证券资本成本）为6%，加上（1.04×4.8%），也就是11%。

资料来源：罗伯斯·帕斯特：《估算预期收益比重的模型博弈》，《金融时报》2001年5月21日。

10.2资本资产定价理论的实证性检验

资本资产定价模型的实际效度可以从以下两个方面来检验：

■通过检验其中哪些基础性假设是不是现实的、是不是符合投资者们的实际行为。

■从实证的角度来检验资本资产定价模型解释实际证券价格现象的程度。

资本资产定价模型以一些极其简单化的假设为基础。很明显，在现实生活中，很多这样的假设（比如说，没有交易成本、对未来的同源性预期，以及投资者之间完全一致的投资时间跨度，等等），都是站不住脚的。然而，不能仅仅以这些原因来否定资本资产定价模型。有可能这些关于现实生活的偏离并不是至关重要的，以至于资本资产定价模型仍然可以有效地解释证券价格波动。正如弗里德曼（Friedman，1953）早已强调过的，只能由一个理论提供的解释，以及一个预测达到一个什么程度的有效性和重要性，来判断这个理论的真实性，这就要求检验该理论与已经观察到的事实之间存在着什么样的逻辑顺序。实际上，一个理论为了提供更有意义、更有用的解释，就必须在某种程度上作出一些描述性不那么现实的假设：这些理论必须从纷繁的事实中抽象出最重要的部分。很少有人会争论说，纽约证券交易所主席的头发是什么颜色，会与解释证券的价格现象有关。但是，问题是那些假设到底有多么不现实呢？要回答这个问题，除了实证地检验这个理论给出的预测是否属实之外别无他法。

回忆一下前几节的内容：资本资产定价模型的主要预测结果，就是市场投资组合是在均值方差效率边界上的。再一次的，这个预测等同于如下预测：所有的证券都在等式10.8给出的那条证券市场线上。大量有关资本资产定价模型有效性的研究都集中在这个预测上。

注意：资本资产定价模型是以投资者对将来收益的预期，或者说未来收益分布来公式化的。如果未来收益分布是已知的，就可以通过检验市场投资组合是否的确刚好位于效率边界上来直接检验资本资产定价模型的效度。然而，在实际生活中，未来收益分布是未知的，因为我们不可能读出投资者脑袋里到底在想什么。在实证研究中，一般都用一组证券的历史或者说既往收益来得出近似的未来收益分布。通过既往收益，可以计算历史均值、方差和协方差，进而构建一个历史效率边界，从而确定市场投资组合相对于该边界的位置。

不幸的是，数据组总是不能完美地表示未来收益分布，这个问题被称为样本误差（Sampling Error）问题。这个问题可能会特别严重，尤其是当时间序列观察的数目相对于证券数目较小的时候。因为有样本误差，既往效率分类（有效率的或是无效率的）不会在逻辑上给出任何真正预期收益分布分类的指标。实际上，从既往的均值—方差来看，市场投资组合都是无效率的，就算这个组合在将来是有效率的。相对于向表现好的超过预料的证券分配高额权重的投资组合，以及向表现得不如预料的证券分配低额权重的投资组合而言，市场投资组合从既往的角度来看，会是无效率的。

为了处理样本误差带来的问题，研究者可以运用统计检验的方法。首先假设市场投资组合是有效率的，这种统计测试一般都会用到一个测试统计数据，以描述数据组违反那个前提假设的程度。一个例子就是，如果把既往均值回归到既往β值时所得的R平方的数值。这个测试数据可以用来测定对无效假设的统计推论（Statistical Inference），也就是说，用来计算市场投资组合是有效率的还是无效率的，这两种情况出现的概率。如果这个P值低于想要达到的重要性水平，比如说5%，那么市场组合就很缺乏效率了，故而就应当拒绝承认资本资产定价模型是一个有效的理论。

我们不可能收集并处理投资市场中所有资产的相关信息。同样，如果用数量很大的一批资产来检测这个理论的效度，就需要大量的观测，以获得可靠的联合收益分布评估。为了达到这个目的，我们常常会根据众多资产的某个共同特征，把它们分成若干个小的基准投资组合（Benchmark Portfolios）。市场资本量或者说规模、估算的β值、账面对市场证券的比率、动量以及工业门类分类，都是在给证券分类时最常用的特征。实证研究通常会包括10～100个基本投资组合。

30多年来，资本资产定价模型一直都在受到严格的实证检验。这些实证研究的动力之一，就是研究人员可以在研究中，运用大规模、高质量的美国股市数据库。这些数据库中最值得注意的，就是证券价格研究中心（CRSP）拥有的数据库。这个金融研究中心位于芝加哥大学商业研究院，该中心建立并一直维护着美国股市的历史资料数据库。在这个数据库里，研究人员可以找到美国股市里单支股票（纳斯达克、美国证券交易所、纽约证券交易所），股市指数，国库券和共同资金产权的相关历史数据。这个高质量的数据库一直在更新，并且没有任何存在资格或者是取消上市（自1999年以来）方面的偏见。

我们在此不能介绍所有的实证研究，因为这些研究在数据集和研究方法方面有很大的差异。这些差异反映了实证研究者们所做的很多选择。其中必须做的有如下几项：

■分析中包括的证券（比如说，所有在纽约证券交易所交易的一般性美国股票）；

■将各种证券归入投资组合的方法（比如说，以账面对市场证券比率为标准进行分类）；

■市场投资组合的代表（比如说，S&P 500指数）；

■收益频率（比如说，月度收益）；

■作为样本的时期（比如说，1926～2003年）；

■统计方法（比如说，下面将要讨论的双传递回归法）。

我们打算简短地讨论一下一种经常被采用的实证研究方法：即所谓的双传递回归法。接下来我们会转而讨论几种股市历史收益系列中反复出现的收益类型，这些类型似乎都与资本资产定价模型不一致。有时，这些类型被称为股市异常（Stock Market Anomalies）。接下来，还将会谈论一些实证检验资本资产定价模型效度的相关研究中存在的一些固有问题。这些问题使得人们会怀疑，以实证的方法来检验资本资产定价模型的效度，到底意义何在，并且又提出了一个问题：到底是不是能用实证的方法来检验资本资产定价模型的效度。

10.2.1　双传递回归法

有很多不同的方法，都可以用来检验资本资产定价模型作出的预测是否能成立。亚洲颇受欢迎的方法就是所谓的双传递回归法。这个方法基本上涉及以下四个步骤：

1.确定样本数据。第一步就是要为基本组合收集一组历史收益数据，给市场投资组合找一个代表（比如说，S&P 500指数），再给无风险利率找一个代表（比如说，1只T券的收益率）。这些数据得在某一个样本时期内，以某一频度（比如说每日、每月或每年）收集得来。这就得出了对n个基本投资组合，市场投资组合和无风险利率的T时间序列观测。

2.估算特征线。第二步就是要用时间序列回归分析单独地估算出每个基本投资组合的特征线（见公式10.7）。用时间序列回归分析估算特征线的做法有时称为第一传递回归，因为它们得出的结果会在第二传递回归（见下）中用到。通常情况下，会用到公式10.10给出的OLS回归评估指数。

3.估算证券市场线。第三步指向对证券市场线的实证评估。具体而言，这一步就是要评估既往市场β值（由上文中的时间序列回归得出）和既往平均盈余收益之间的交叉关系。既往盈余收益被视为未来预期盈余收益的评估指数。为了达到这个目的，就要用到下列的回归模型：

为了检验资本资产定价模型得出的预测是否准确，也同样可以在投资组合中包含不会影响预期收益的因素。这种例子之一就是β值的平方，即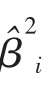。如果资本资产定价模型是一个有效的理论，那么这个变量就应该没有解释效力，因为资本资产定价模型预测到了在均值和β值之间存在一种线性关系。这样的例子包括非市场风险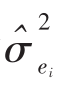，也就是源于非市场因素或因具体公司的具体情况而不同的风险。按照资本资产定价模型，非市场风险应该没有解释力，因为只有系统风险才能被定价：

在此公式中，γ₂计量了β值平方的影响，γ₃计量了非市场风险的作用。

4.检验资本资产定价模型作出的预测。最后一步就是要决定估算的证券市场界线的属性是不是与资本资产定价模型预测到的相一致。如果资本资产定价模型是有效的，那么证券市场界线的截距就应该为零，也就是说γ₀＝0，并且证券市场界线的坡度应该等于资产酬金，也就是γ₁＝［E（R_m）－r］。我们可以通过查看，估算的回归系数与资本证券定价模型所预测的值之间是不是有很大的不同，来检测这一点。^[20]更进一步的，资本资产定价模型要求β值是唯一一个可以解释预期收益的变量，也就是说均值和β值之间应该存在最佳拟合关系。如果所有的预期收益对子和β值都落在证券市场界线之上，那么市场就处于平衡状态。然而，当历史数据被用来估算预期收益和β值时，一般而言有些证券会落在证券市场界线的上方或者是下方，这就表示市场处在不平衡的状态，或者就是一种从统计学上而言对于该线不重要的偏离（这种偏离的原因是样本误差）。测试实质性证券市场界线的R平方是不是大大低于效用。

此外，与非线性市场风险相联系的术语，比如说β值平方，或者说非市场风险应当没有解释力，并且，回归系数不应当大幅度地偏离零。

应用这几个分析步骤的例子

为了说明以上谈到的这个分析流程，我们把这个流程应用到美国股市中的1只样本股票上。具体说来，用权重CRSP全股票指数作为市场投资组合，以1个月就到期的美国T券作为无风险证券。整个投资界都被总结成10个基于市场β值的价值权重基本投资组合。每年的12月底，所有的证券都以它们的历史β值为标准进行排序，进而形成了10个β值投资组合。在所有的股票中，有10%拥有最低的β值，把这些股票放到一起就构成了投资组合1。依此类推，一直到投资组合10，在这个投资组合中，有占所有股票10%的股票，它们的β值是最高的（见表10.10）。收集这些投资组合在1935年1月～1968年6月之间的所有月度收益数据，这个时间段和法玛与麦克白（Fama&Macbeth，1973）所用的数据时间段是一致的。^[21]

图10.11以图形的形式说明了这些结果。图10.11（a）是均值—标准差点阵图。该图包括了单个基本投资组合（图中所示的那些空心的点），以及市场投资组合（M）。这个点阵图是以样本均值、方差和协方差构成的。虚线代表风险债券的效率边界（没有无风险证券）。很明显，市场投资组合与效率边界离得很近。与此不同的是，市场投资组合离无风险证券（黑线）的效率边界却比较远。利用以无风险利率贷入的资金，并把已经有的资金投资到相切投资组合（T）中，似乎有可能达到较高的风险收益选择效果。

图10.11（b）是均值—β值点阵图。图中直线代表的是回归线，也就是那条给出均值和β值之间最佳拟合的直线。回归线有三个重要的属性：

■正如β值描述的，预期收益与市场风险之间存在一种积极的正向关系，也就是说，高风险是和高收益相联系的。

■这种关系是线性的，也就是说β值每增长一个单位，预期收益也就有相同的增长。在估算的证券市场界线中，其截距为0.463，这反映了相对于零β值投资组合，每月多出的预期盈余收益为0.463%，也就是说每年为5.5%。在实证得出的证券市场界线中，其

表10.10　10个以β值分类的投资组合的描述数据

图10.11　10个以β值分类的投资组合的实证性结果

坡度为0.489%，这反映了每月0.489%的市场风险酬金率，也就是每年5.9%的酬金率。

■这种关系近乎于确切的，也就是说除了β值以外，没有其他东西可以决定预期收益了。调整后的R平方大致是90%，也就是说存在一个近乎完美的拟合。几乎所有投资组合平均收益之间的交叉性差异，都可以用它们市场β值之间的差异来解释。

这三个属性反映了如下事实：市场投资组合距离风险债券组合效率边界很近。然而，注意回归线的截距是0.463%。这个截距从实证的层面估算了超过零β值投资组合收益的那个预期盈余收益。在这种情况下，这个截距就大大高于0。意味着零β值投资组合带来的预期收益率大大地高于无风险利率。此外，回归线的坡度（0.489%）大大低于超过市场投资组合的平均盈余收益（0.953%）。它反映了以下事实：在无风险利率存在的情况下，市场投资组合将会远离效率边界。如果无风险借贷是允许的，那么打点的那条线代表的就是这种条件下预期到的证券市场界线。

总结一下，以这个数据组为基础，平均收益与市场β值之间就表现出了一种近乎完美、积极的线性关系，因为截距在很大程度上与无风险利率不同，并且坡度也比资产酬金要低。

10.2.2　与资本资产定价模型不一致的异常情况

很多研究者都已经做了类似的测验。早期的检验结果似乎与资本资产定价模型是一致的。^[22]然而，在这些测验中，代表二者关系的截点太高了，坡度又太平了，这些都与最初的夏普—立特勒模型不一致。但是，如上所述，这些结果却与布莱克的零β值模型相一致，在该模型中不允许无风险的贷入资金。在他们的结果发布之后，资本资产定价模型得到了学者们和股票交易从业者们的一致支持。尽管如此，此后不久就发现了许多似乎与资本资产定价模型并不一致的经济学现象。下列三种股市中的异常情况就是这些现象中被讨论得最多的。

规模效应

市场资本规模（低封顶）小的公司似乎会赚取正量的异常平均收益，而高封顶的却会赚取负的异常收益。^[23]如果仅以资本规模来对投资组合分类，规模效应（Size Effect）一般不会很强烈。这是因为资本规模和β值之间的联系很紧密，小公司典型地都会高估β值。然而，如果我们给投资组合做一个二次分类，第一次以β值来分，第二次以资本规模来分，那么规模效应一般都会出现。在β值可比的情况下，低封顶的公司股票一般会比高封顶的公司股票表现得更好。据估算，低封顶的公司股票带来的异常收益在每一宗生意的2%～4%之间。在20世纪60～70年代，资本规模酬金是讨论最多的话题。

价值效应

第15章讨论了一些股票估价中经常会用到的估价形式，比如说，价格对收入的比率（P/E），股息对价格的比例（D/P），以及账面对市场证券的比率（B/M）。相对于与公司相关的基本条件（比如说收入、股息和账面价值）而言，有较高市场价值的股票被称为“上涨股”。注意：股票基金有较高的P/E值，较低的D/P值以及B/M值。与此相反的是，“有价证券”相对于与公司相关的基本条件而言，有较低的市场价值，也就是说有较低的P/E值，较高的D/P值以及B/M值。价值效应（Value Effect）并不表示以下情况是真实的：有价证券似乎会赚取高水平的异常平均收益，而上涨股只会赚取负的异常收益。^[24]据估算，有价证券的异常收益比率一般都在每宗4%～6%之间。

趋势效应

正如第12章中讨论的，根据效率市场理论的原理得出的预测说明，我们不能预测异常收益。然而，似乎却可以从既往的收益中预测到异常收益。粗略地说，在短期内，也就是说在1年之内，遭受损失的投资者还会继续遭受损失，而获利的投资者仍然会继续获利。^[25]趋势效应（Momentum Effect）甚至比规模效应和价值效应更强，据估算，每宗交易带来的异常收益在4%～6%之间。然而，在某种程度上，趋势效应也可能会被夸大。

试考虑以下事实：

■纯趋势策略要求有很高的周转率。结果交易成本和税收可能会大大削弱趋势效应带来的好处。

■大多数“盈利者减亏损者”趋势组合的收益都是由于亏损者表现得太差所致。所有为了描述一大堆趋势效应带来的结果，就需要用到短缺头寸。这对于一般投资者而言是不太现实的。

■趋势效应在低封顶股票中会表现得比较强，这就趋向于使这些股票不那么容易转成现金。试图把高周转率策略运用于低封顶的股票是不现实的。这几点表明，也许趋势效应并没有给投资者带来一个赚取异常收益的真正机会，至少最近的结果是这样显示的。

有趣的是，趋势效应在较长的时期内，也就是说在几年的时间里，会逆转过来。具体而言，在长时期内表现得都很好的股票会趋向于在接下来的一段时期内表现得较差，而长期以来表现不佳的股票则会趋向于在稍后的时期内价格上扬。^[26]

总结一下，相对于包含有较多低封顶股票、有价证券和既往盈利者，而只含有较少高封顶股票、上涨股以及既往亏损者的投资组合而言，一般用来代表市场的投资组合在均值—方差层面上，似乎是非常没有效率的。与此相联系的是，市场协方差似乎只解释了平均收益中的一小部分较差变化，而资本规模、BE/ME值以及动量似乎表现出了更有实质性意义的解释力。

可以用基于资金规模的BE/ME值组成的美国股票投资组合带来的历史收益来说明这些问题。具体而言，我们又一次会用到CRSP全股指数代表的市场投资组合，用1个月就到期的美国国库券来代表无风险证券。至于单个的风险债券，用所谓的法玛和弗伦奇组合来代替，这个组合是基于资金规模和BE/ME值而构建的。具体做法是把所有在美国证券交易所、纽约证券交易所以及纳斯达克上市交易的单支股票，按照资金规模大小归入5个类别之中，从规模最小的到规模最大的股票进行排序。同时，再把所有在以上交易所交易的单支股票按照BE/ME值归入5个类别之中，从低BE/ME值（上涨股）到高BE/ ME值（有价证券）进行排序。如此，一共得出了25个投资组合，用的是1963年7月～2002年12月期间的474个月度收益数据。^[27]

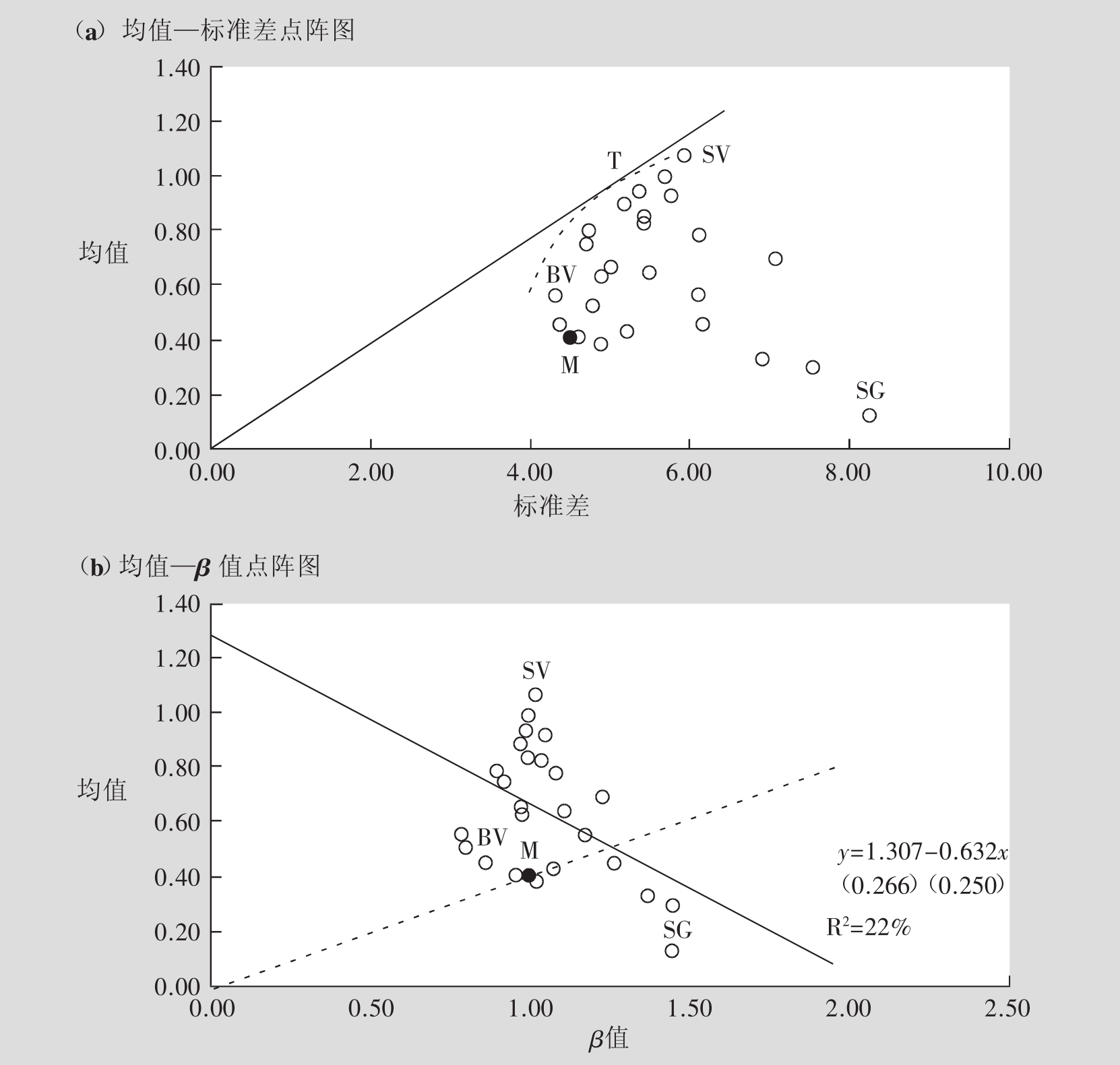
图10.12　对规模和价值异常的描述说明

图10.12（a）是这个数据集的均值—标准差点阵图。很明显，从均值—方差分析的结果来看，市场投资组合是极其没有效率的。这个结果违反了均值—方差资本资产定价模型的中心预测：市场投资组合在均值—方差分析中的有效率性。图10.12（b）是那25个基本投资组合的均值—β值点阵图。均值和β值之间的关系很弱。R平方只有22%，也就是说只有22%的方差可以用β值来解释。如果资本资产定价模型是有效率的，那么我们就可以预测到R平方值应该不会比整体小得太多了。然而实际得出的R平方值却似乎并不比0大多少！同样，均值和β值之间存在一种负的而非正向的关系。因此，可以有很高的置信度来否定资本资产定价模型的有效性。注意：对于证券市场界线的偏离程度直接与资金规模和BE/ME值有关，低封顶的股票和有价证券位于证券市场界线以上的区间之内，而高封顶的股票以及上涨股则有系统地位于其以下的区间内。

10.2.3　研究方法问题

几个研究方法方面存在的问题引发了以下的两个问题：现存的测验（也就是既包括那些支持资本资产定价模型的，也包括那些对于资本资产定价模型不利的测验）是不是真实地检测了资本资产定价模型的有效性；以及资本资产定价模型的有效性是不是一开始就是可以测验的。

基准误差

在被称为“罗尔批判”的作品中，罗尔（Roll，1977）列举了一系列的逻辑问题，对于那些旨在测验资本资产定价模型有效性的实证研究本身是不是有效而提出了质疑。正如本章前面讨论的，市场投资组合包括了世界上所有的资产，而这些资产各占有与其市场价值相适应的组合权重。在实际生活中，一般我们并不知道市场投资组合的确切构成，相反，我们只用了一个具体的组合来代表市场投资组合。这种代表典型的只含有一个下级分支证券群组。比如说，很多研究都用美国一般股票指数（比如说，S&P 500指数）来代表市场投资组合。这样一来就排除了，受投资者青睐的股票、美国股市以外的股票、国债、房地产、商品贸易以及人力资本等。同样，这些研究中，分配给投资组合各证券的权重，也常常与该证券的市场价值不相适应。比如说，有几个研究用的就是等权重投资组合，而不是市场价值权重投资组合。罗尔指出，在研究中用到一个下级分支证券群组可能在资本资产定价模型本身就是错误的情况下，仍然会得出测验数据来表明它是正确的，也可能在它本身是正确的情况下，得出测验数据说它是错误的。如果在分析中给各资产分配的投资组合权重不适当的话，也会发生这样的错误。

再次重复，资本资产定价模型预测到，市场投资组合在均值—方差分析中是有效的，或者，这个预测的等效预测，也就是说均值和市场β值（证券市场界线）之间存在最佳的拟合关系。针对这个预测，罗尔做出了以下两点重要的说明。

第一，假设不论真正的市场投资组合是否是有效的，都用一个在均值—方差分析中有效率的、包括所有单支证券的投资组合来代表它。如果β值是相对这个代表市场投资组合的投资组合而计算出来的，那么可以发现均值和市场β值之间一直存在着最佳拟合关系。因此，发现市场β值和均值之间有最佳拟合关系的实证研究只能表明，一个有效率的投资组合（落在效率边界上的投资组合）在该研究中被选为市场投资组合的代表。与此相反，有的实证研究发现，此二者之间没有那么完美的联系，这也只能说明，在研究中，代表市场投资组合的那个组合是无效率的投资组合（位于效率边界以内的投资组合）。

第二，为了要检验市场投资组合是否是有效的，需要包括所有的资产，并以它们的市场价值为基础，分配各自的投资组合权重。既然我们不知道市场投资组合确切的构成情况，资本资产定价模型就是不能检测的。现有的对资本资产定价模型效度的测验，其实是在检验代表市场投资组合的那个组合是不是有效的，而不是在检测真正的市场投资组合是否是有效的。总结一下，上面的论述也就是说如果资本资产定价模型不是真的，我们也有可能会接受它，把它当成一个有效的理论（如果用来代表市场投资组合的那个投资组合是有效的话）；如果资本资产定价模型本身是真的，我们也有可能不承认它，把它当成一个无效的理论（如果用来代表市场投资组合的那个组合本身是没有效率的话）。因此，只有在市场投资组合的构成情况是已知的前提下，才可以检验资本资产定价模型是否是一个正确的理论。

不幸的是，就算是资本资产定价模型是有效的，而且真正的市场投资组合也是完全有效的，对市场投资组合的些许偏离，比如说，排除某些证券或者给投资组合中的那些证券分配了错误的组合权重，就已经足够使均值和β值之间的拟合程度变得很差了。相反，就算资本资产定价模型是一个无效的理论，并且真正的市场投资组合也极其没有效，对市场投资组合的极小偏离也已经足够产生一个均值和β值间的最佳拟合了。问题就是投资组合权重里的小变化会带来单支证券β值的巨大改变。罗尔和罗斯（Roll&Ross，1994），坎德尔和斯坦博（Kandel&Stambaugh，1995）以及格劳尔（Grauer，1999）都指出与此类似的现象在收益分布中也时有发生。

要点就是：我们不能符合逻辑地从一个代表市场投资组合的组合是不是有效的这一事实推导得出市场投资组合的效率性分类是怎样的，因为有效性分类对投资组合的构成情况极其敏感。因此，需要知道市场投资组合的确切构成情况（包括其中所有证券的确切身份以及每一支证券各自确切的相对市场价值）。不幸的是，在实际生活中，我们从来不知道市场投资组合的确切构成是怎样的。对于可以交换贸易的证券而言，也许还可以从该证券投放到市场中的数量和市场价格方面的信息来计算市场价值。然而，对于那些非交易性的证券，比如说人力资本，一般都没有数量和价格方面的确切信息。因为这个原因，它们在市场投资组合中到底占有多大的权重还是很不确定的事情。因此，资本资产定价模型在实际操作层面上来说是一个不能被验证的理论。

我们强调：对于代表市场投资组合的那个敏感性问题的讨论是一个逻辑推理问题，而不是一个统计学推理的问题。问题不是我们观测的数据不够多，从而不能从统计学的角度很好地估算β值，而是投资组合权重的细微变化都会导致β值的巨大改变。所以，就算是在真实总体均值和β值都是已知的情况下，或者就算样本数目足够大，进而准确地估算出了β值，罗尔的批判还是适用的。

罗尔批判对实证检验资本资产定价模型的研究提出了很大的质疑。举例说，假设某些实证研究并不反对如下的一个无效假设：S&P 500指数在均值—方差分析的层面上来看是有效的，因为该指数中各单支证券的均值和方差之间有很强的联系。这个假设并不能证明市场投资组合是有效率的，因为S&P 500指数排除了一些像低封顶股票，不在美国股票市场交易的股票、国债、房地产、人力资本、商品货物、现钞这样一些证券，而只要把上述的这些证券类型包括在内，结果就会有不同了。类似的，如果否认S&P 500指数的有效性也不会提供反对资本资产定价模型的有力证据。

对于基本偏误问题，一种可能的反应就是试图找出那些被省略掉的证券类型，再找出其中一个相适应的收益来代表它们的总体收益情况，最后把这个代表运用到分析中去，从而解决这个问题。比如说，贾纳森和王（Jagannathan&Wang，1996）曾以总体劳动收入变化比率为基础得出了一个代表人力资本变化的量，并把这个量运用到研究中，在他们的模型里除了价值权重股票市场指数的β值以外，还包括有劳动收入增长的β值。

类似的问题也会发生，因为研究中用到的是基本投资组合而不是单个资产。具体而言，就算是能够给基本投资组合都正确地定价，我们还是不能保证每一个资产都会因此而被正确地定价。此外，如果单个资产的定价是正确的，但是这些资产在基本投资组合中的权重并不是和它们各自的相对市场价值相互适应的，那么这个基本投资组合仍然可能会被错误地定价。不幸的是，还没有简单的方法可以解决这个问题，因为我们不太可能可靠地估算出数目众多的单个资产会有什么样的联合收益分布。

收益分布随时间推移而发生的改变

再一次重复，我们一般都不知道预期收益分布的情况，因此只能用既往的观测数据来代表未来的分布情况。能从既往数据中得出什么样的结论取决于这些观测的统计学分布情况。一种可能的假设就是把这些观测都当成是从预期分布中随机得来的，并且假设市场投资组合不会随着时间的推移而改变。在这种情况下，历史收益分布情况从统计学上来说是预期收益分布的良好评估参照。然后通过检验既往均值和既往β值之间的关系来确定时常的效率性。这个关系允许用统计学的原理来推断那个真正的关系（预期均值和β值之间的真实关系）。

程和格劳尔（Cheng&Grauer，1980，1982）提出了一个有力的观点，他们认为就算资产收益分布是恒定的也不能据此假定β值也是恒定的。我们知道不同的资产有不同的既往收益情况。这些差异会转变成相对市场价值的变化或者市场投资组合构成情况的改变。此外，市场投资组合构成的改变又会导致β值的改变。我们已经知道就算是市场构成只有些微小改变也足以引发β值的巨大改变。

进一步地说，有大量的证据显示：收益分布（预期收益、方差和协方差）会随着时间的推移而发生改变。收益分布中的部分改变是和商业循环联系在一起的。比如说，经济衰退时期的风险收益水平都较高。这也许反映了一个简单的事实，就是说在生活艰难的时候还要花钱来支付商品消费主观上会遭受很大的痛苦。与此相反，风险酬金水平在经济扩张时期都较低。同样，资产的相对风险水平也会随时间的推移而改变。比如说，一些公司如果大幅举债收购，也就是说这些公司有比较高的负债产权比例，那么它们的股票就会更有风险，在经济衰退时期，这些股票之间的相关度水平也会提高。如果忽略无风险利率随时间推移而发生的变化，市场风险酬金和β值就可能会严重地影响到回归结果，降低拟合程度。

如果收益分布会随着时间的推移而发生变化，这种变化又会带来什么实际的问题呢？如果这个分布会随时间的推移而变化，那么每一对市场投资组合的观测代表的都是一个与不同条件性分布相联系的最优化问题。然而，市场投资组合一般不代表与无条件分布相联系的最优化解决方法。换句话说，如果允许投资者随着经济情况的变化而更改他们投资组合的构成，那么一般而言就不会在所有的经济情况下都选择一种固定不变的投资组合构成。如果投资者利用他们掌握的有关经济形势的信息，并且以无条件分布为基础来做出投资决策，那么他们的生活就会比忽视所有的信息并且以无条件分布为基础来做出投资决策所能过上的生活更好，也就是说可以做出更好的风险—收益选择。与此相类似的是，如果我们在离家外出前听了天气预报，一般都会做出更好的决定；然而如果忽视了天气预报提供的信息，那么也许我们一年到头都得随身带着外套和雨伞了，就算是可以预测到明天将有一个万里无云的高温天气也是如此。这肯定不是一个问题的最优化解法。如果市场投资组合都代表与无条件分布联系的最优化解法，那么就没有理由去预测无条件均值和无条件β值之间存在一个确切的正线性关系。实际上，我们可以发现均值和β值之间的任意一种关系类型——或弱或强的关系，正关系或者负关系。如果我们把讨论集中在无条件分布上，市场风险酬金与β值正相关的资产，也就是说市场风险酬金高时β值也高的证券，会倾向于赚得正量的异常收益。比如说勒陶和路德维格森（Lettau&Ludvigson，未发表的论文）表示，有价证券在经济衰退中（此时市场风险收益水平也高）有较高的β值，而且这种衰退，由于商业循环的变化，会带来超常的价值效应。关于这个问题更细致的讨论可以参见第17章的相关内容。

对于这种随着时间的推移而发生的变化，一种可能的反应就是想用一个由少量观测构成的移动窗口来收集数据，以便解释收益分布随时间的推移而发生的机构性改变，最终达到解决这个问题的目的。比如说，法玛和麦克白（1973）通过每月单独观测得出了基本投资组合的盈余收益。在一个回归模型中，他们把这个盈余收益值回归到通过前60次月度观测估算出的β值上。这个方法留给人一个很难做的选择。如果流动窗口的规模过大，那么随时间的推移而产生的变化也许不能被排除。比如说，如果以5年为期的话，观测到的数据也许会同时包括经济衰退和经济扩张时期。相反，如果窗口的规模较小，那么就不能得到足够的观测数据进而可靠地估算收益分布了。

另外一个可能的方法就是建立一个模型分析收益动态。具体说来，可以一方面估算β值和市场风险之间的关系；另一方面建立一个商业循环评估指数。这里有几个经常用来说明这些评估指数的例子，包括T券收益率、信誉差以及期限差，等等。这种方法有效地尝试着去恢复条件投资组合概率，还允许检测市场投资组合是否在每一个时间点上相对于条件分布而言都是有效率的。

这个理论的缺点之一就是：经济学理论只是在很小程度上对具体化汇报动态具有指导意义。这些理论给出了一些预测，比如说在经济衰退期里会出现低风险利率和高市场风险酬金。然而，没有一个模型可以确切地描述收益动态。另外一个问题就是，描述或者预测商业循环的宏观经济学变量数据在质量方面不及金融市场数据那么高：这种变量数据不是能那么经常地收集得到的，并且这些数据也因为对它定义常常会改动而易于变化。实际上，吉赛尔（Ghysels，1998）在大多数情况下具体化不良的证券定价模型相对于无条件性模型而言都会产生更大的估价偏误。

与预期收益函数图像相关的另外一个问题和相关投资时间跨度的选择有联系。雷夫哈瑞和利维（Levhari&Levy，1977）表示，用月度数据估算出来的β系数和用年度数据估算出来的β系数不太一样。既然它们不一样，那些实证研究的结果就取决于研究中用的是哪种估算传统得出的数据了。科萨瑞等人（Kothari et al.，1995）认为年度β值比月度β值更合适，因为一个投资者的投资时间跨度较之一个月而言更接近于一年。他们表示用年度数据估算β值时，β值和收益间的关系会更强。

测试方法中的统计问题

要检验资本资产定价模型的预测是否正确，有许多种统计技术可以用。在这些统计技术中，首先都有一套对观测得来的收益数据统计学分布情况的假设。每一种统计技术都是在这些假设条件之下，试图找到一些最好的统计学评估指数。如果这些假设都不正确，那么估算的结果也许就会是完全不可靠的了，尽管这个模型本身表明了这些结果是完全可信的。某些检验资本资产定价模型效应的实证结果——既有支持资本资产定价模型的证据，也包括反对资本资产定价模型的证据——也许会反映出在实验中运用了不适当的统计技术。

我们在先前曾经粗略地介绍过，双传递回归法至少可能有两个计量经济学上的失误。首先，它的步骤依靠OLS回归法。这种回归法向每一个观测分配相等的权重。从计量经济学上讲，如果所有的误差项都有相同的方差（同源偏差性），并且这些误差项之间都是相互独立的（没有序列相关性），那么这种处理数据的方法就还是有意义的。用经济学的术语来讲，第二传递回归的意思就是必须假定所有的证券都有相同的非市场性风险，并且每一支证券的非市场性风险都与其他所有证券的非市场性风险相互独立。在很多情况下，这些假定都被推翻了。比如说，市场风险（β值）高的证券一般都会有高水平的非市场性风险，而不同证券的非市场性风险，又都包括了来自于工业发展潮流、汇率、利率和商品价格变动对于证券价格带来的影响。在这些情况下，我们就不能向所有的观测者分配相同的权重。相反，统计技术应该向非市场性方差小，并且与其他证券之间非市场性协方差小的证券分配较高的权重。反过来，我们应该向非市场性方差大，并且与其他证券之间非市场性协方差大的证券分配较低的权重。

另一个问题就是，我们独立地对待了在第一传递回归中的β值估算与第二传递回归中的实际证券市场界线估算这两个环节。这样一来，第二传递回归就忽略了从第一传递回归中得来的误差。从计量经济学的角度而言，这种做法很有问题，因为这个测试流程会混有计量误差和定价误差以及对证券市场界线的偏离这三个不同的概念。可以通过这两种误差之和最小化的那条线一般都不会使定价误差之和降到最小，也就是不能给出证券市场界线的最佳近似值。实际上，我们可以证明这个问题导致了第二传递回归的截距偏离0，导致估算出的坡度偏向0，而偏离的程度取决于误差在变量中的相对重要性。同样，如果β值的测量有失误，以及如果非市场性因素与真正的（未知）β值相关，那么这些因素可能会表现得很有影响力。米勒和斯科勒斯（Miller&Scholes，1972）通过一个控制得很好的模拟试验说明，如果我们在研究中用的是单支证券，这个问题就会引发非常具有欺骗性的估算结果。这就是要用充分多样化的基本投资组合而不是单支证券的一个重要原因。在充分多样化的投资组合中，很多对单支证券β值估算的失误都互相抵消了，因而投资组合的β估算值会更加准确。

忽视这些重要的问题可能会导致偏差严重的估算结果。为了绕过这些问题，我们可以用更为先进的统计技术，比如说汉森（Hensen，1982）的归纳型矩方法（GMM）。归纳型矩方法技术有效地考虑了同时估算β值和证券市场界线的问题。此外，这个方法还可以解释非市场性风险中的差异和依存关系。

不幸的是，合适的统计技术取决于我们对观测到的收益数据的统计发布有什么样的假定。不幸的是，资本资产定价模型没有提出关于这个分布的有力预测，因为这个模型没有详细地指出那些观测的方差—协方差项，以及这些项是如何随着时间的推移而演进的。

数据筛选、数据窥探和样品选择偏好

数据筛选（Data-mining）指的是通过广泛的搜索模型和数据集而找出数据类型的方法。在实证研究中，可能都得接受错误地否定一个假设的概率。显著性水平给出了错误地否定一个对某个模型和数据组的假设接受的概率。如果尝试了足够多数量的模型和数据集，那么肯定有些主要的模型会碰巧出现。当一个研究者不说明在最终报告那个成功的类型之前，检测了多少个不同的模型和数据集时，数据筛选中的问题就出现了。同样，数以百计的研究者，为了要发表论文，就花费大量的时间去寻找股票收益和其他变量之间的关系。只有那个成功的测验被提交和发表，而没有成功的测验则再也不能重见天日。

数据窥探（Data-snooping）就是查看过去的实证研究结果以指导未来的研究。其结果就是在数据中，只是随机类型的组合可能有意义。数据窥探可以是追逐数据类型的协调活动，这种活动在几个分析者共同研究同一数据时，会变得不那么准确。解决这个问题的办法就是研究新数据。

因为经验性研究是建立在历史数据基础上的，而且资产市场是彼此高度相关的。因此，所有研究员本质上都是在考虑完整的数据集或非常相似的数据集，这些数据在时间上相互交迭，并包含与先前研究的资产高度相关的资产。一些研究已经表明，从数据调查方面产生的偏离的数量可以是很大的。具体来说，基准投资组合建立在公司特征这一先决条件（公司规模以及BE/ME）上，我们知道公司特征是与预期利润相关。例如，公司规模以及BE/ME的影响作用在重要的法玛和弗伦奇研究之前是很知名的。此外，将这些投资组合按公司特征分类反过来人为地增大了个总投资组合间的不同。

如果数据的可获得性导致某些资产从分析中被排除，就可能产生样品选择偏好（Sample-selection Bias）。例如，众所周知，Compustat数据库遭受了生存偏好，由于企业被增加到数据库的方式的原因，就如由本兹和布林（Banz&Breen，1986），布林与格拉吉兹克（Breen&Korajczyk，1994）和克瑟雷（Kothari et al.，1995）^[28]等描述的。企业被典型地放入Compustat文件中，带有几年的历史数据。因为在某一指定年期间增加到数据库的企业是仍然存在的企业，再一次填写先前几年的历史数据就对那些在这些年一直存在的企业产生了偏离。那些在这些年中破产的和没有在数据库中出现的企业从没有包括进来。这一依过去经济发展形势分析的选择偏离会对股票收益交叉选择研究产生重大作用。许多有关财务的研究发现与公司基础有关的核算方法的低市场价格股票能带来反常的高于平均收益。如果使用收集账户数据的数据集排除那些失败的公司，那么就可能出现样品选择偏离。克瑟雷等调查了这个问题并认为，失败的股票会被预计有低收益和高的B/M比率。如果排除失败的股票，那么那些具有高B/M比率的股票是包括在内的。他们表示这种偏离是形成对早先关于平均收益和B/M比率关系的研究结果的原因。增加从Compustat被排除的企业到数据库中会减弱B/M的解释力，并且甚至可能消灭它。

一个公司股票从一个交易中移出（将股票名称从交易所上市股票名单中除去）也可能使一个样品产生偏离。例如，芝加哥大学的证券价格研究中心（CRSP）是学术研究领域中利润数据的主要提供者。当股票名称移除发生时，CRSP尝试收集从表上删除公司的收益，但CRSP经常无法收集到这些收益并且必须将它们列为丢失。一项由苏伟和瓦尔特（Shumway&Wharter，1999）开展的最新研究用文件为CRSP纳斯达克回归数据记录了由股票名称移除产生的偏离。作者表示，与劣绩公司（例如破产）联系在一起的股票名称移除往往比与佳绩或中性公司相关的股票名称移除（例如合并或转向其他交易）丢失率更高。另外，股票名称移除更频繁地发生在小公司上。

10.3　结论：有效还是无效

许多研究员设法测试资本资产定价模型的有效性。研究大多数集中于这一预期：由价值衡量决定的市场投资组合是平均变化有效的，也就是说，所有单个资产都取决于证券市场界线（其中资产手段与β值之间具有精确的、正相关线性关系）。早期关于美国股市的研究显示的确存在这样一种关系。对于这一关系所截取的部分太高并且斜率太小，因此与原始的夏普—立特勒模型并不相一致。然而，其结果与布莱克的零β值资本资产定价模型是一致的，这一模型中没有考虑零风险借款（见10.2.1节）。但是，在过去30年中，许多研究结果涌现出来对以上发现产生质疑。首先，一定数量的经验主义的股市反常现象被发现；看起来我们能通过增加小额资本、价值股票和相对于市场价值而言过去的优胜者来击败市场（在风险和收益之间达到一种更加有利的交易，见10.2.2部分）。其次，有几个方法学上的问题开始质疑当前的测试是否当真是对资本资产定价模型的测试，以及它到底是不是可测试的。这些方法学上的问题包括合适的市场投资组合和基准投资组合的选择，利润分配的时间变化，以及适当地对统计方法的选择，还包括一些数据处理问题，譬如数据筛选，数据窥探和样品选择偏好（见10.2.3节）。根据这些新发现，我们不能对资本资产定价模型的经验主义的有效性得出一个毫不含糊的结论。一些研究员认为，资本资产定价模型是没有生命力的，并且他们转向了其他的资产定价模型，包括一般资本资产定价模型、多时间段资本资产定价模型、基于消费的资本资产定价模型、套利价格理论（APT）（见第11章）以及行为财政学的模型（见第12章）。而有一些人则认为，要是资本资产定价模型，考虑了市场投资组合中的人力资本并且对利润分配的周期变化做出说明，这一模型还是适用的。其他人等待更有意义的测试，仍然有人认为资本资产定价模型根本不具有可测试性，因为它没有指定譬如市场投资组合的成分以及随时间变化的动态利润这些关键因素。

看起来这场论战不会很快结束。尽管如此，资本资产定价模型始终是投资理论的基础之一，并且它成为获得许多选择财产定价的模型的依据，并且是许多可选择的资产定价模型的基础，也是计量其他可选模型的经验主义的有效性基准。

并且，资本资产定价模型在选择投资组合、业绩评估、风险管理和资本预算等方面得到广泛应用。本书中有关这些主题的章节将阐明从业者赋予资本资产定价模型的重要性。例如，α值和β值被广泛应用于投资组合选择。β值是一个普遍的衡量市场时机（Market Timing）的值。如果一个投资者要买进股票，而又担心股市会在短期内滑坡，那么最佳的方案就是投资低β值的股票。相反，在股市上扬时，高β值会给投资者带来高于平均的利润收益。α值对于证券选择（Security Selection）很有用，因为它表明哪些股票可能带来反常利润收益和对介入风险的合理补偿。

同样，α值和β值对于业绩评估（Performance Evaluation）很有用。投资组合选择是把眼光投向未来，而业绩评估则是着眼于过去。在共有基金情况下，基金的α值和β值使投资者能够评估资金管理者是否称得上他们赚得的薪资（高α值），还是仅仅跟着市场的尾巴走（牛市期间的高α值或熊市期间的低β值）。

β值常被用作风险管理（Risk Management）的（系统）风险措施，例如第21章讨论的价值风险框架。β值的吸引力之一是它能凭借一个数值来判断一种资产对其他可获得资产的依赖程度。相反，在第8章谈到的平均变化框架中，这种依赖度要通过（n-1）协方差来求得。β值通过与其相关的市场价值来判断每种资产的协方差，对于一个很好的多变投资组合来说，这是一件很敏感的事情。从这个角度来说，资本资产定价模型是减少信息负担以及全面平均变化框架估算的有效工具。

除了投资组合选择，业绩评估和风险管理，资本资产定价模型在社团财政决定方面也很有用。企业需要估测其资本成本来评价新投资方案［资本预算（Capital Budgeting）］。财务经理可以采用资本资产定价模型来计算资产净值成本，它是资本成本的一项主要成分。此外，在没有市场估价的机构中，很需要有资本成本预测。不管是因为资产净值成本是由个人持有还是因为所指的公共交易实体还没有成型（例如：IPOs，吞并或将子公司股票分配给母公司股东）。

总的来说，从业者认为资本资产定价模型是有用的。而大部分从业者也认为资本资产定价模型不够完善；他们知道要获得可靠的α和β估计值是很难的（评估误差），也清楚资本资产定价模型只是一个排除了许多现实的可能因素的简单模型。因此，尽管资本资产定价模型用途广泛，作为风险衡量的β值和作为额外收益衡量手段的α值的用途，在本书的后面部分还将看到，从业者们在选择、监控、管理他们的投资组合方案时还是会采用其他的辅助工具。

理论联系实际10.2

FT

估算预期收益的模型权衡

不完善模型

资本资产定价模型仅仅是一种模型，它并不对现实情况进行完善的描述。实际上，许多学术研究都否认了它的有效性，因为一些股份收益模式看起来与资本资产定价模型这一模式很不协调，甚至二者互相矛盾。但是这难道就意味着我们应该完全摒弃这种模型，去依赖于那种无模型可言的评估方法吗，比如说按样品的平均盈利？不！无论哪一种模式根据定义或者说是概念都是“错误”的，因为它们仅对我们这个复杂的世界做了较为简单的推测。但是尽管如此，就算是一种不确切的模式，它在某种程度上也是有用的。对于我们采用贝叶斯（Bayesian）观点并用预先猜测的方法来综合得到的数据是非常有用的。因为通过对这种样品的平均收益的分析，这些数据可以告知我们预期收益（在GM每年14%），预先猜测可建立在像资本资产定价模型这样的金融理论上（在GM每年11%）。估算的结果是这两个数字的加权均值。这一度量取决于对这一模型的信任程度以及这种模型同数据相比所具有的优越性。这种贝氏估算方法被罗伯特·斯坦博（Robert Stambaugh）在其研究中得到了发展。研究发现，就算对某种定价模式比如资本资产定价模型信心不大时，资本成本的估算也应该依赖于这一模型。平均股份收益的估算方法不太准确，所以还是少用为好。也就是说在估算预期股份收益时，理论比数据更重要，更有说服力。

更为复杂的是，资本资产定价模型并不是仅有的一种估算预期收益的理论模式。与其共存的还有一种多因素模式。根据这一模式，预期收益取决于股票的β值，而这又和除了市场因素以外的许多因素有关。这些相关因素可以是宏观经济变量（比如，由陈南福，理查德·罗尔和史蒂芬·罗斯［Nai-fu Chen，Richard Roll&Stephen Ross）发展起来的一种5个因素的模式］，或者是建立在公司性质上的［比如，尤金·法玛和肯·弗伦奇（Eugene Fama&Ken French）的3个因素的模式］，甚至也可能是使用统计技术，比如因素分析得出的收益级数。究竟哪种模型最好，大家还各持己见，没有最后的标准。鉴于这种情况，我们又该怎么做呢？有一种较为明智的解决方法就是通过对各种模式估算得出的结论分析建立一种平均预期加权收益值，这些模式包括那种产生样品平均估算的“无理论”模式。而无论哪种估算方法都是建立在一种可能性上的，那就是它们的母体模式必须是正确的。那么将如何得到这种可能性呢？它能帮助我们注意到相关的研究，但其结果还是一种判断问题。作者认为，尽管资本资产定价模型有其不尽如人意之处，但它具有最强的理论依据，应当引起最广泛的关注。其他各种模式应当根据其理论依据和使用结果来评判其好坏。

不确定性

尽管定价模式通常来说产生的是预期收益，而且这种预期收益比起样品平均收益也更为准确，但它仍有其不确定性。法玛和弗伦奇的研究表明每年有3%以上的错误都产生在对资产净值的工业成本的估算上，而在这一过程中采用的模式就是普通定价模式。而这些不确定性又是如何产生的呢？而我们不知道这种不确定性的根源是否又比其他一些情况更为重要呢，比如说，我们不清楚真正的β值和资产额外费用的真正价值，我们也不确定究竟哪一种是正确的模式。

有趣的是，总体上来说，不清楚每种模式内部的参数竟然比不知道哪种模式正确更为重要。这是作者通过对上述资产成本研究得出的结论。因此应该把时间更多地用在努力去改善各种模式上，而不是把时间都浪费在试图寻找一种正确的模式上去。另外，对额外费用的不确定性要大于对β值的不确定性，这种情况使这一无形的资产额外费用成为公司资产估算成本中不确定因素的最大根源。

尽管资产估价模式在经济上应用较为广泛，但它并不是估算资产仅有的选择。另外一种模式在美国被经常应用于调节效用上，它是以戈尔丹（M.J.Gordon）增值模式为基础的（戈尔丹于1962年对这种模式进行了描述）。这样资产成本就等于当前的股息收益与长期的股息增值率之和。由于很多原因，并不为学术界青睐。这种方法做了一个假设，即股息将永远以同一种比率进行增值。另外，也不存在一种理论来估算股息增值率，而这种情况是非常不幸的，因为资产成本估算对股息增值率非常敏感。因此，这一估算方法能够很好地反映一个公司的前景。

移动目标

最近，学术界正兴起一种意见，即预期收益将随时间的变化而变化。例如，预期股份收益看起来和商业周期相关，即在商业不景气时较高，景气时较低。在所有这些迄今为止发现的有助于解释预期股份市场收益中随时间而变化这一现象的不定因素中，就有D/P比率和E/P比率的综合因素。如果这些比率低，就将预示着收益低。也就是说，当估价相对较高时，未来的收益总体上就会较低，尤其是从长远来看未来的10年内都将保持这种低收益的状态。去年出现了这样的情况，即当D/P比率和E/P比率降到最低时，S&P 500指数降低了10%，因此，D/P比率和E/P比率的预测能力也得到了增强。但是，这种预测在1990年表现得并不准确，因为当时出现了较低的D/P与E/P和较高的股份市场收益共存的情况。

“如果你对数据进行了充分的研究，你最终能从中得出规律”，诺贝尔奖获得者经济学家罗纳德·考司（Ronald Coase）这样说道“如果能寻找到多种不定因素，将能从中发现一种能够预测收益的不定因素”。但是，这种表面上的可预测性的存在是偶然的，而且像这种重视数据的不定因素在将来也是不起作用的。一个非常有趣的例子就是由彼德·科伊（Peter Coy）提供的一篇文章，他在文章中引用了一家货币管理公司的经理大卫·雷爱伯（David Leinweber）的一句话。雷爱伯曾说：“通过对联合国软盘记录的仔细审查以及对历史的分析，S&P 500指数中最好的预测者就是孟加拉国的黄油生产。”如果你想以此发财，那就祝你好运。

幸运的是，经济学家们已找到了D/P和E/P比率具有预测能力的原因。但是难题依然存在。那就是，这种预测关系是线性的吗？估算这种关系中的未知参数的最佳方式是什么？以及还要考虑的其他的预测方法是什么？

如果在预期收益较为稳定时对它的预测还有困难的话，那么当它随时间而变化时预测就更难了。估算预期收益没有一个简单的秘诀。由于数据有时并不准确，而且任何理论也都不是十全十美的，因此在估算过程中的几个关键点上，就需要评判介入。考虑到预期收益的重要性和与其相关的严重不确定性，很显然，金融行业还需在其估算中投入更多。这种投入将无可置疑地产生一个较高的预期收益。但是请不要向我打听这个确切的数字。

进一步阅读

Chen N.，R.Roll and S.Ross，1986，‘Economic Forces and the Stock Market’，Journal of Business，59，383-403.

Coy，P.，1997，‘He Who Mines Data may Strike Fool’s Gold’，Business Week，16 June.

Fama，E.F.and K.R.French，1997，‘Industry Costs of Equity’，Journal of Financial Economics，43，153-193.

Pastor，L.and R.F.Stambaugh，1999，‘Costs of Equity Capital and Model Mispricing’，Journal of Finance，54，67-121.

Pastor，L.and R.F.Stambaugh，‘The Equity Premium and Structural Breaks’，Journal of Finance，56，1207-1239.

Scholes，M.and J.Williams，1997，‘Estimating Betas from Nonsynchronous Data’，Journal of Financial Economics，5，309-327.

资料来源：罗伯斯·帕斯特：《估算预期收益比重的模型均衡》，《金融时报》2001年5月21日。

链接

这篇文章是这个有关“投资”章节中一篇文章的第三部分，也是最后一部分。在这一部分，作者讨论了资产估价理论的使用，包括基本的资本资产定价模型理论，目的在于将其应用于实践来估算预期收益率。他最后进行了总结，即根据理论进行的估算比简单地对历史各年的收益进行的抽样平均估算法更为精确。要想得到精确的估算结果，就应当把理论和历史上各年收益数据以及相关评判结合起来进行考虑。

总结

理解资本市场界线，只包括有效率的投资组合

投资者可以把任何风险资产和无风险资产进行混合，从而创造更多的投资机会。而投资机会又完全依赖于机会线。所有的投资者，如果不考虑其同好曲线，都将从坡度最大的机会线中选择一个投资组合。这条线就是资本市场界线。所有处于资本市场界线上的投资组合都是高效的，而且它们都是由各种不同的市场投资组合和无风险资产共同组成的。

理解分离资产

这种投资组合的选择程序可以分为两个步骤，第一步是选择最佳的风险资产的投资组合；第二步是选择步骤一中已选定的投资组合与无风险资产的最佳混合体模式。在步骤一中，不必考虑同好曲线，因为每个投资者都是选择同样的投资组合，但是在第二个阶段中就需要考虑到同好曲线。

理解为何证券市场界线表现的是风险和预期收益率之间在资本资产定价模型中的均衡关系

在二者的均衡状态中，所有的资产、个人股份和投资组合都处于一条证券市场界线上。根据资本资产定价模型的理论，资产风险（β值）越高，预期收益就越高，资产都显示在证券市场界线上。在均衡状态中所有的资产都得到了准确估价。任何对证券市场界线的脱离都意味着市场不处于资本资产定价模型的均衡状态中。

解释检验资本资产定价模型的双传递回归法

检验资本资产定价模型在实际应用效果中的一种较为流行的方法就是双传递回归法。这种方法使用第一传递回归来分别检验每种基准资产或者投资组合的特征线，使用第二传递回归来综合检验所有资产或投资组合的证券市场界线。在使用这种方法的过程中，一些研究者发现了资本资产定价模型的实际依据。但是，也有一些人则发现了同资本资产定价模型在体系上相互矛盾的其他一些模型。其中之一就是同市场资本化相关的股市反常，账面到市场资产净值比率和要素。

解释为何检验资本资产定价模型是否能很好地体现资本市场很困难的原因

有许多方法性的问题值得思考，即现存的检验方式是否是对资本资产定价模型的真正检验，以及资本资产市场究竟是否能够被检验。这些方法性问题包括对适当的基准投资组合和市场投资组合的选择、收益分布的时间变化、适当的统计方法的选择，以及数据问题，比如数据筛选、数据窥探和样品选择偏好。在当前实际结果的基础上，还不可能对资本资产定价模型的实际效果得出较为清晰的结论。一些研究者认为资本资产模型已经形同虚设，于是这部分人便转向了其他一些模型，包括套利定价理论、一般资本资产定价模型、多时间段资本资产定价模型和基于消费的资本资产定价模型。还有一些人认为，资本资产定价模型仍然有效，尤其是在把人力资本纳入市场投资组合之后，以及在对收益分布的周期变化进行解释之后。另一些人则在等待一个更有意义的检验方法的出现，也有人依然认为资本资产定价模型从原则上来讲根本不具有可检验性。

理解从业者如何应用资本资产定价模型

很多从业者认为资本资产定价模型依然有效，但其效用已不那么活跃。资本资产定价模型在实际中得到了广泛的应用，比如，投资组合的选择、业绩评估、风险管理和资本预算。尽管如此，很多从业者仍然认为资本资产定价模型的估算效果不好，即他们清楚利用这种定价模型很难能够得到对α值和β值的可靠的估算（估算错误），并且资本资产定价模型只是一种简单的定价模型，它没有考虑实际应用中可能会出现的很多情形。因此，尽管资本资产定价模型得到了广泛的应用，以及β值在测量风险中的应用和在α值测量额外收益中的应用，从业者也在使用附加工具对他们的投资组合进行选择，监测和管理。

关键词

异常收益300

旺盛资产296

α值300

资产定价理论286

基准投资组合313

资本资产定价模型287

资本预算327

资本市场界线293

特征线297

评估系数304

基于消费的资本资产定价

模型309

数据筛选325

数据窥探325

防御资产296

均衡收益率286

误差项297

盈余收益297

一般资本资产定价模型307

多时间段资本资产定价模型308

负债投资组合292

市场β值296

市场投资组合287

市场风险298

市场时机326

趋势效应318

中性资产296

非市场风险298

机会线290

业绩评估327

定价误差300

回归分析303

R平方304

无风险资产287

风险管理327

样品选择偏好325

样本误差312

证券市场界线299

证券选择327

分离原则288

夏普比率292

规模效应317

标准误差304

统计推论313

股市异常313

系统风险298

相切投资组合293

三矩资本资产定价模型309

非系统风险298

价值效应318

β值292

无风险利率盈余收益297

资产298

零β模型307

练习题

1.解释下列与资本资产定价模型相关的问题：

a.解释资本资产定价模型中的分离法则。

b.风险测量中的β值度量标准是什么？

c.股份中的α值是什么？

d.描述一下证券市场界线（SML）。

e.描述一下资本市场界线（CML）。

2.假设在股份A中有以下数据和市场投资组合：

a．计算β_A。

b．计算σ²_A。

c．分别计算系统和非系统的风险组成。并用恰当的术语讨论这些风险。

3.假设某个市场投资组合有以下一些参量：E（R_m）=10%，σ_m=10%。你有一个有效的投资组合σ_p=20%，并且它的平均收益是15%：

a．你是往外贷还是往内借？

b．无风险利率是多少？

4.尽管资本资产定价模型存在一些不切实际的假设而且很难在实际中进行检验，虽然已在实际中得到了广泛的应用。讨论一下资本资产定价模型的用途？

5.讨论资本资产定价模型中三个最明显的矛盾，也就是资本市场中的股市异常。

若想获得练习题的参考答案，请访问Levy-Post投资网站，网址为：http://www.booksites.net/levy

参考文献

Banz，R.W.，1981，‘The Relationship between Return and Market Value of Common Stock’，Journal of Financial Economics，9，3-18.

Banz，R.W.and W.J.Breen，1986，‘Sample-Dependent Results Using Accounting and Market Data：Some Evidence’，Journal of Finance，41，779-793.

Basu，S.，1977，‘Investment Performance of Common Stocks in Relation to their Price-Earnings Ratios：A Test of the Efficient Market Hypothesis’，Journal of Finance，32，663-682.

Basu，S.，1983，‘The Relationship between Earnings Yield，Market Value and Return for NYSE Common Stocks：Further Evidence’，Journal of Financial Economics，12，129-156.

Black，F.，1972，‘Capital Market Equilibrium with Restricted Borrowing’，Journal of Business，45，444-455.

Black，F.，1993a，‘Beta and Return’，Journal of Portfolio Management，20，8-18.

Black，F.，1993b，‘Estimating Expected Return’，Financial Analysts Journal，49，36-38.

Black，F.，M.C.Jensen and M.Scholes（1972），‘The Capital Asset Pricing Model：Some Empirical Tests’，In：Jensen，M.C.，editor，Studies in the Theory of Capital Markets，New York：Praeger，79-121.

Breeden，D.，1979，‘An Intertemporal Asset Pricing Model with Stochastic Consumption and Investment Opportunities’，Journal of Financial Economics，73，265-296.

Breeden，D.，M.Gibbons and R.Litzenberger，1989，‘Empirical Tests of the Consumption-Oriented CAPM’，Journal of Finance，44，231-262.

Breen，W.J.and R.A.Korajczyk，1994，‘On Selection Biases in Book-to-Market Based Tests of Asset Pricing Models’，Working Paper 167，Northwestern University，Chicago，IL.

Campbell，J.Y.，2000，‘Asset Pricing at the Millenium’，Journal of Finance，55，1515-1567.

Chan，L.K.C.，Y.Hamao and J.Lakonishok，1991，‘Fundamentals and Stock Returns in Japan’，Journal of Finance，46，1739-1789.

Cheng，P.L.and R.R.Grauer，1980，‘An Alternative Test of the Capital Asset Pricing Model’，American Economic Review，70，660-671.

Cheng，P.L.and R.R.Grauer（1982），‘An Alternative Test of the Capital Asset Pricing Model:Reply and Further Results’，American Economic Review，2，1201-1207.

Chopra，N.，J.Lakonishok and J.R.Ritter，1992，‘Measuring Abnormal Performance：Do Stocks Overreact？’，Journal of Financial Economics，31，235-268.

DeBondt，W.F.M.and R.H.Thaler，1985，‘Does the Stock Market Overreact？’，Journal of Finance，40，557-581.

Fama，E.F.，1996，‘Multifactor Portfolio Efficiency’，Journal of Financial and Quantitative Analysis，31，441-465.

Fama，E.F.and K.R.French，1992，‘The Cross-Section of Expected Stock Returns’，Journal of Finance，47，427-465.

Fama，E.F.and K.R.French，1996，‘Multifactor Explanations of Asset Pricing Anomalies’，Journal of Finance，51，55-84.

Fama，E.F.and J.Macbeth，1973，‘Risk，Return and Equilibrium：Empirical Tests’，Journal of Political Economy，81，607-636.

Friedman，M.，1953，‘The Methodology of Positive Economics’，in Essays in Positive Economics，Chicago，IL：University of Chicago Press.

Friend，I.and M.Blume，1973，‘A New Look at the Capital Asset Pricing Model’，Journal of Finance，28，283-299.

Ghysels，E.，1998，‘On Stable Factor Structures in the Pricing of Risk：Do Time-Varying Betas Help or Hurt？’，Journal of Finance，53，549-573.

Grauer，R.R.，1999，‘On the Cross-Sectional Relation between Expected Returns，Betas and Size’，Journal of Finance，54，773-789.

Grundy，K.and B.Malkiel，1996，‘Reports of Beta’s Death Have Been Greatly Exaggerated’，Journal of Portfolio Management，23，36-45.

Hansen，L.P.，1982，‘Large Sample Properties of Generalized Methods of Moments Estimators’，Econometrica，50，1029-1064.

Harvey，Campbell R.and Akhtar Siddique，2000，‘Conditional Skewness in Asset Pricing Tests’，Journal of Finance，55，1263-1295.

Jaffe，J.，D.B.Keim and R.Westerfield，1989，‘Earnings Yields，Market Values，and Stock Returns’，Journal of Finance，44，135-148.

Jagannathan，R.and Z.Wang，1996，‘The Conditional CAPM and the Cross-Section of Expected Returns’，Journal of Finance，51（1），3-53.

Jegadeesh，N.，1990，‘Evidence of Predictable Behavior of Security Returns’，Journal of Finance，45，881-898.

Jegadeesh，N.and S.Titman，1993，‘Returns to Buying Winners and Selling Losers：Implications for Stock Market Efficiency’，Journal of Finance，48，65-91.

Kandel，S.and R.F.Stambaugh，1995，‘Portfolio Inefficiency and the Cross-Section of Mean Returns’，Journal of Finance，50，157-184.

Kothari，S.P.，J.Shanken and R.G.Sloan，1995，‘Another Look at the Cross-Section of Expected Returns’，Journal of Finance，50，185-224.

Kraus，Alan and Robert H.Litzenberger，1976，‘Skewness Preference and the Valuation of Risk Assets’，Journal of Finance，31，1085-1100.

Lettau，M.and S.Ludvigson，2002，‘Time-Varying Risk Premia and the Cost of Capital：An Alternative Implication of the Q Theory of Investment’，Journal of Monetary Economics，49（1），31-66.

Lettau，M.and S.Ludvigson，‘Expected Returns and Expected Dividend Growth’，unpublished paper.

Levhari，D.and H.Levy，1977，‘The Capital Asset Pricing Model and the Investment Horizon’，Review of Economics and Statistics，59，92-104.

Levy，H.，1978，‘Equilibrium in an Imperfect Market：A Constraint on the Number of Securities in a Portfolio’，American Economic Review，68，643-658.

Lintner，J.，1965a，‘Security Prices and Maximal Gains from Diversification’，Journal of Finance，20，587-615.

Lintner，J.，1965b，‘The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets’，Review of Economics and Statistics，47，13-37.

Lo，A.W.and A.C.Mackinlay，1990，‘Data-Snooping Biases in Tests of Financial Asset Pricing Models’，Review of Financial Studies，3，431-467.

Lucas，R.，1978，‘Asset Prices in an Exchange Economy’，Econometrica，46（6），1426-1445.

Mackinlay，A.C.，1995，‘Multifactor Models Do Not Explain Deviations from the CAPM’，Journal of Financial Economics，38，3-28.

Maginn，J.L.and D.L.Tuttle，1990，Managing Investment Portfolios：A Dynamic Process，2nd edn，New York：Warren，Gorham&Lamont.

Markowitz，H.M.，1990，‘Normative Portofolio Analysis：Past，Present，and Future’，Journal of Economics and Business，42（2），99-103.

Merton，R.C.，1973，‘An Intertemporal Capital Asset Pricing Model’，Econometrica，41，867-887.

Merton，R.C.，1987，‘A Simple Model of Capital Market Equilibrium with Incomplete Information’，Journal of Finance，42，483-510.

Miller，M.and M.Scholes，1972，‘Rates of Return in Relation to Risk：A Reexamination of Some Recent Findings’，in M.Jensen，ed.，Studies in the Theory of Capital Markets，New York：Praeger，47-78.

Mossin，J.，1966，‘Equilibrium in a Capital Asset Market’，Econometrica，34，768-783.

O’Neal，E.S.，1997，‘How Many Mutual Funds Constitute a Diversified Mutual Fund Portfolio？’，Financial Analysts Journal，53（2），37-46.

Roll，R.，1977，‘A Critique of the Asset Pricing Theory’s Tests，Part 1：On Past and Potential Testability of the Theory’，Journal of Financial Economics，4，129-176.

Roll，R.and S.A.Ross，1994，‘On the Cross-Sectional Relation Between Expected Returns and Betas’，Journal of Finance，49，101-121.

Rosenberg，B.，K.Reid and R.Lanstein，1985，‘Persuasive Evidence of Market Inefficiency’，Journal of Portfolio Management，11，9-17.

Ross，S.A.，1976a，‘The Arbitrage Theory of Capital Asset Pricing’，Journal of Economic Theory，13，341-360.

Ross，S.A.，1976b，‘Risk，Return，and Arbitrage’，In：I.Friend and J.Bicksler，editors，Risk and Return in Finance，Cambridge，MA：Ballinger，189-218.

Rudd，A.and H.K.Clasing，Jr，1988，Modern Portfolio Theory：The Principles of Investment Management，2nd edn，Orinda，CA：Andrew Rudd.

Sharpe，W.F.，1964，‘Capital Asset Prices：A Theory of Market Equilibrium’，Journal of Finance，19，425-442.

Sharpe，W.F.，1991，‘Capital Asset Prices with and without Negative Holdings’，Journal of Finance，46，489-510.

Shumway，T.and V.Wharter，1999，‘The Delisting Bias in CRSP’s NASDAQ Data and its Implications for the Size Effect’，Journal of Finance，54，2361-2379.

附录有关资本资产定价模型的一个形式证明

根据分离原则，所有的投资者都有同样的高效投资组合（市场投资组合），由于这种投资组合依据平均变化标准是有效的，它就成为解决下列问题的方法：

总结一下，这个问题涉及的是把差异最小化，并受制于市场投资组合的平均数的投资组合，并且在这一投资组合中所有的资产都必须投入进去。^[29]

我们应该直接解决这一问题，说明证券市场界线是最佳的解决方法。但是，为了把这一说明简单化，有必要来考虑以下问题：

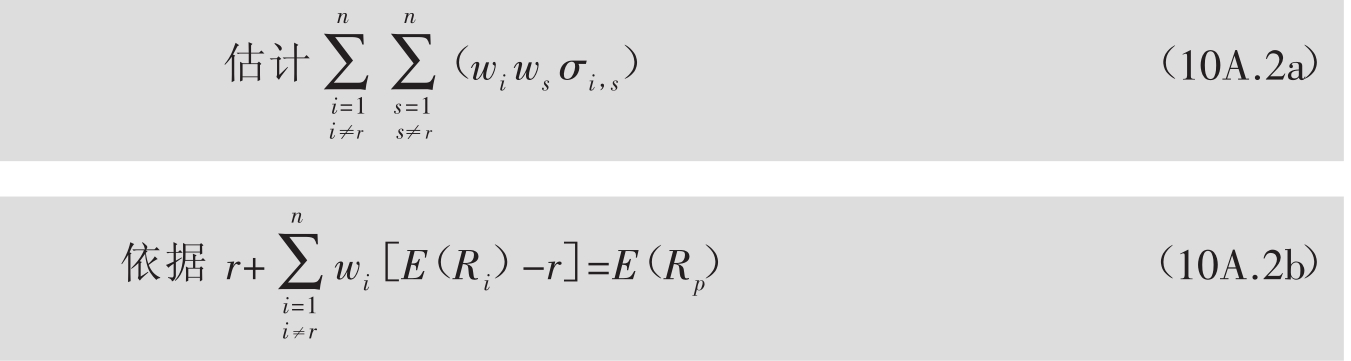
这个问题排除了无风险资产的权重而只包括风险资产的权重。这就意味着我们可以排除权重必须合成为①的限制（10A.1c）。如果风险资产的权重大于1，那么就简单地借贷这个差异；如果小于1，投资者则简单地把这个差异借出去。排除所有财产都必须投入的限制就能使这一问题简单化。但是，我们必须通过代替这一公式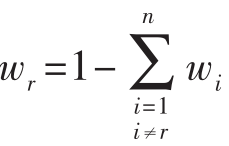来改变客观函数（10A.1a）和（10A.1b）中的市场投资组合平均数中的限制。这就产生了经过调整的客观函数10A.2a和经过调整的限制10A.2b。

既然已经把这个问题简单化了，现在就开始解决它吧。问题10A.2a-b是所谓的突起二次性程序问题，对于这样的问题，可以通过解决最佳化情形找到最好的解决方法。为了达到这一目的，我们可以建立下列拉格朗日函数：

在这一函数中λ是一个拉格朗日乘数，它表示的是（10A.2b）中均值限制的假定价格；如果增加所需的平均数，它就可以测量最佳投资组合差异的增加。拉格朗日函数关于投资权衡w_i的首要派生是：

首要情形表现的是最佳情形，是在选择权重量的时候发现的，而对于这个权重量所有首要的派生都是零，即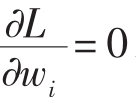，i=1，…，n。所以，投资组合权重中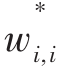=1，…，n的投资组合才是最佳的，其前提是

或者：

既然这一等式适用于所有的资产，它可用于市场投资组合，这里β_m=1，因此：

或者：

代替公式（10A.5）中的λ得出：

用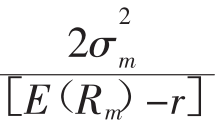同除两边，得到证券市场界线：

这就完成了证明。总结，证券市场界线是市场投资组合平均方差最小的最优的一阶条件。

【注释】

[1]The variance of the riskless asset is σ²_r=E（rr）-E（r）E（r）=r²-r²=0.Similarly，the covariance of the riskless asset with the ith asset is σ_r，i=E（rR_i）-E（r）E（R_i）=rE（R_i）-rE（R_i）=0.

[2]Curve LZ represents the set of all points between L and Z on the mean-variance frontier.The segment AL represents the inefficient part of the frontier.

[3]Using differential calculus，we can show that the first-order derivative of the variance of the market portfolio with respect to the weight of the ith asset is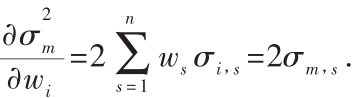Hence，the covariance with the market measures the sensitiv ity of the variance of the market portfolio to small changes in the portfolio weights.

[4]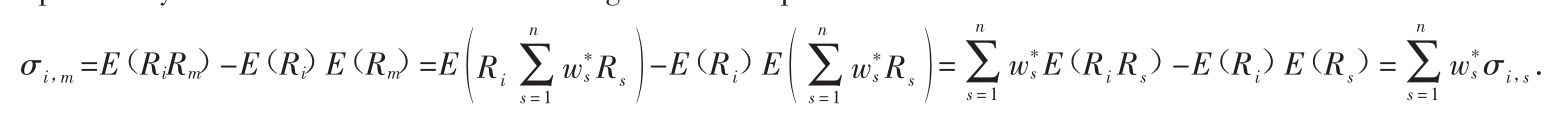Specifically，this follows from the following chain of equalities：

[5]See Appendix A at the end of this book for an introduction to regression analysis.

[6]Section 10.1.6 will show that alpha（α）has an economic meaning；it measures the return in excess of the riskadjusted return，as implied by the CAPM，and therefore is called the abnormal return.

[7]The characteristic line measures the expected excess return on the ith asset for a given R_m.Thus，for any R_m，a point on the line is given by R_i=α_i+β_iR_m.If R_m is，say，10%and β=2 and α=5%，we have R_i=5%+2×10%=25%. However，if R_m changed from 10%to 14%，then the expected excess return on the stock would be R_i=5%+2×14%=33%，and the change in the expected excess return would be 8%，as a beta of 2 would predict.

[8]By taking expectations of both sides of the characteristic line（Equation 10.7）and using E（e）_i=0，we find E（R）_i-r=α_i+[E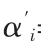（R_m）-r]β_i or α_i=E（R）_i-r-[E（R_m）-r]β_i.By contrast，if we use R_i=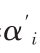+β_iR_m+e_ifor the characteristic line，then we find=E（R）_i-E（R_m）β_i.The two alphas are related in the following manner: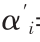=α_i-（1-β）_ir.

[9]This follows from the following chain of equalities：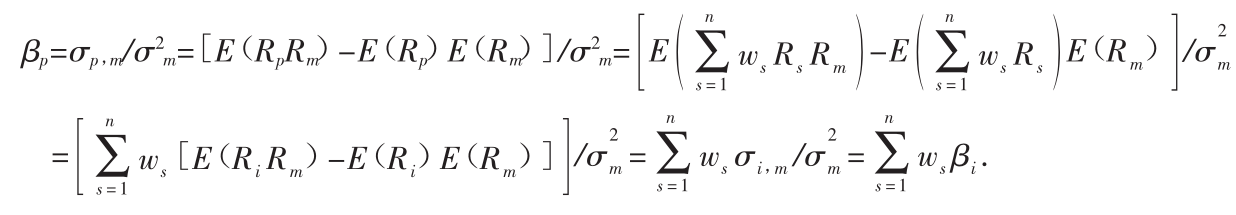

[10]This expression follows from the variances and covariances of the terms in the right-hand side of Equation 10.7. Since α_i and β_i are constant，their variances and covariances are zero.Also，in regression analysis，the regresso（rRm_t）is independent of the error term（e_it）.Hence，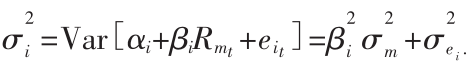

[11]Appendix 10 contains a formal proof of the SML.

[12]The market risk premium is the expected excess return on the market portfolio，or[E（R_m）-r].This premium is sometimes referred to as the beta premium or the equity premium.

[13]For a mix of the riskless asset and the market portfolio，R_p=w_rr+（1-w_r）R_m，where w_r is the investment proportion in the risk-free asset.In this case σ_p=（1-w_r）σ_Rmand β_p=（1-w_r）β_m=（1-w_r）×1.Thus，as w_rdecreases，both σ_pand β_pincrease at the same rate.

[14]The market return，the industry definitions and industry returns used to compute the results are obtained from the homepage of Kenneth French（www.mba.tuck.dartmouth.edu/pages/faculty/ken.french/）.The risk-free rate is obtained from Ibbotson.

[15]The mean-variance-efficient set is‘convex’，i.e.if two（or more）portfolios are efficient，then a weighted average of those portfolios is also efficient.

[16]A problem in testing and implementing the GCAPM is the need for information on the portfolio composition and the wealth level of each investor.

[17]The ICAPM can be difficult to test and implement because it requires detailed information on the way that the return distribution changes through time or the return dynamics.Unfortunately，economic theory does not put forward strong predictions on this topic.

[18]Despite the intuitive appeal of the consumption-based model，empirical tests have not supported its predictions（see Breeden et al.，1989）.Accordingly，consumption-based asset pricing has not received as much attention in practice as the CAPM.One difficulty in using this model is problems in measuring the rate of growth in per-capita consumption. Consumption data generally are substantially less reliable than transaction data on financial assets.For example，statistics are reported on expenditures rather than consumption，which ignores the important effects of consumption from durable goods and storage of non-durables.

[19]Note that this estimation method assumes that the errors for the different assets have the same distribution and that they are mutually independent.In many cases，this assumption is violated and other estimation methods are needed；see Section 10.2.3.

[20]For this purpose，we can use the t-test and F-test discussed in Appendix A at the end of this book.

[21]The market return is obtained from the homepage of Kenneth French（www.mba.tuck.dartmouth.edu/pages/faculty/ ken.french/）.The risk-free rate is obtained from Ibbotson.The beta portfolios are taken from the data library of Pim van Vliet at www.finance-on-eur.nl

[22]Using more recent data，the relationship between mean and beta is much weaker and the market portfolio seems mean-variance-inefficient relative to beta-sorted porfolios.

[23]Black et al.（1972），Friend and Blume（1973）and Fama and MacBeth（1973），among others.

[24]See，for example，Banz（1981）and Fama and French（1992）.

[25]See，for example，Basu（1977），Basu（1983），Jaffe et al.（1989），Rosenberg et al.（1985），Chan et al.（1991）and Fama and French（1992）.

[26]See，for example，Jegadeesh（1990），Jegadeesh and Titman（1993）and Fama and French（1996）.

[27]See，for example，DeBondt and Thaler（1985）and Chopra et al.（1992）.

[28]The data on the market portfolio and the benchmark portfolios are taken from the homepage of Kenneth French（www. mba.tuck.dartmouth.edu/pages/faculty/ken.french/）.The Treasury bill data are from Ibbotson.

[29]Black（1993a，1993b）suggested that the results of the famous Fama and French（1992）study of the size and B/M effects were likely an artefact of data-mining.Since Fama and French chose their explanatory variables based on the results of earlier empirical studies，the observed explanatory power of these variables could be due to a massive data-mining exercise on the part of the authors of these earlier studies.Based on this，Black contended that some of the statistical tests in Fama and French（1992）were not specified properly.He also suggested that since the relations between returns and size and B/M were likely an artefact of data-mining，then they wound disappear if another time period or another data source were analysed.Mackinlay（1995）also mentions data-mining as a potential cause of the observed results.