市场组合的平均风险报酬率

9.1　风险的衡量

投资者和公司在做投资决策的过程中，风险是一个关键的影响因素，因此，量化投资所产生的风险非常重要。风险通过股票回报率的标准差（σ）来衡量，通过历史回报率或期望的未来报酬率进行计算。

9.1.1　通过概率计算风险和报酬

表9.1给出了股票A和股票B的可能的报酬率及其相应概率，字母含义如下：

表9.1　股票A和B的报酬率及其概率

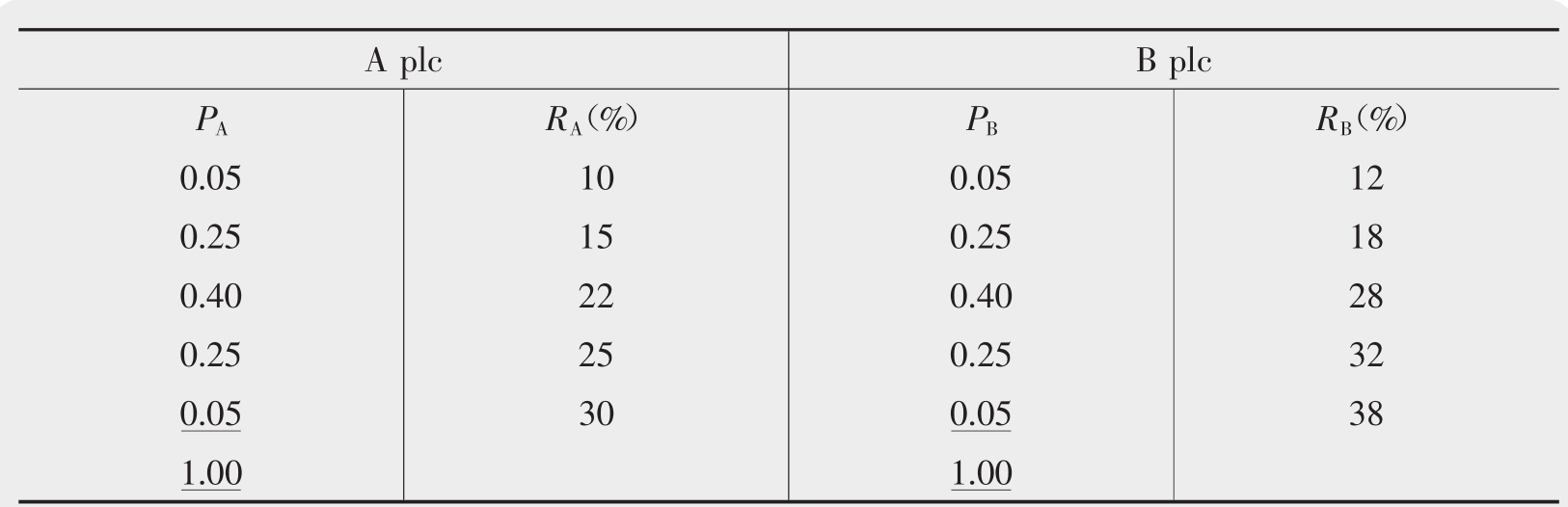
P_A表示股票A的报酬率出现的概率

R_A表示股票A的报酬率

P_B表示股票B的报酬率出现的概率

R_B表示股票B的报酬率

通过下面的公式可以计算出两种股票的平均报酬率和标准差：

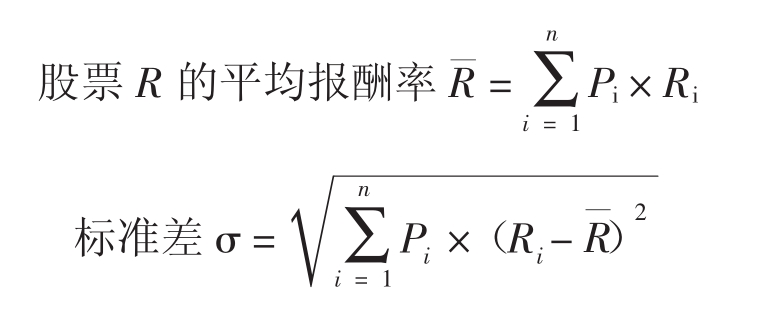
字母含义如下：

P₁，…，P_n表示n种不同结果的概率

R₁，…，R_n表示与n种不同结果相应的报酬率

通过上述公式和提供的信息，我们可以计算出每种股票的平均报酬率和每种股票的标准差。

股票A的平均报酬率：

（0.05 × 10）＋（0.25 × 15）＋（0.40 × 22）＋（0.25 × 25）＋（0.05 × 30）＝20.8%

股票B的平均报酬率：

（0.05 × 12）＋（0.25 × 18）＋（0.40 × 28）＋（0.25 × 32）＋（0.05 × 38）＝26.2%

股票A的标准差：

［0.05 ×（10 - 20.8）²）+ 0.25 ×（15 - 20.8）²+ 0.40 ×（22 - 20.8）²

+ 0.25 ×（25 - 20.8）²+ 0.05 ×（30 - 20.8）²］^1/2= 4.84%

股票B的标准差：

［0.05 ×（12 - 26.2）²+ 0.25 ×（18 - 26.2）²+ 0.40 ×（28 - 26.2）²

+ 0.25 ×（32 - 26.2）²+ 0.05 ×（38 - 26.2）²］^1/2= 6.60%

由此可见，尽管与股票A相比，股票B有较高的平均报酬率，但是相应地也有较高的风险水平。

9.1.2　利用历史数据计算风险和报酬

通过下列公式可以计算出某个股票每年历史报酬率的标准差和平均值：

表9.2是股票S和股票T过去5年的历史报酬率的详细数据表。

根据历史报酬率和上述公式：

股票S的平均报酬率：

［6.6＋5.6＋（－9.0）＋12.6＋14.0］/5＝5.96%

股票T的平均报酬率：

［24.5＋（－5.9）＋19.9＋（－7.8）＋14.8］/5＝9.10%

股票S的标准差：

［ （6.6 - 5.96）²+（5.6 - 5.96）²+（-9.0 - 5.96）²+（12.6 - 5.96）²+ （14.0 - 5.96）²/5］^1/2= 8.16%

股票T的标准差：

表9.2　两种股票S和T的历史报酬率

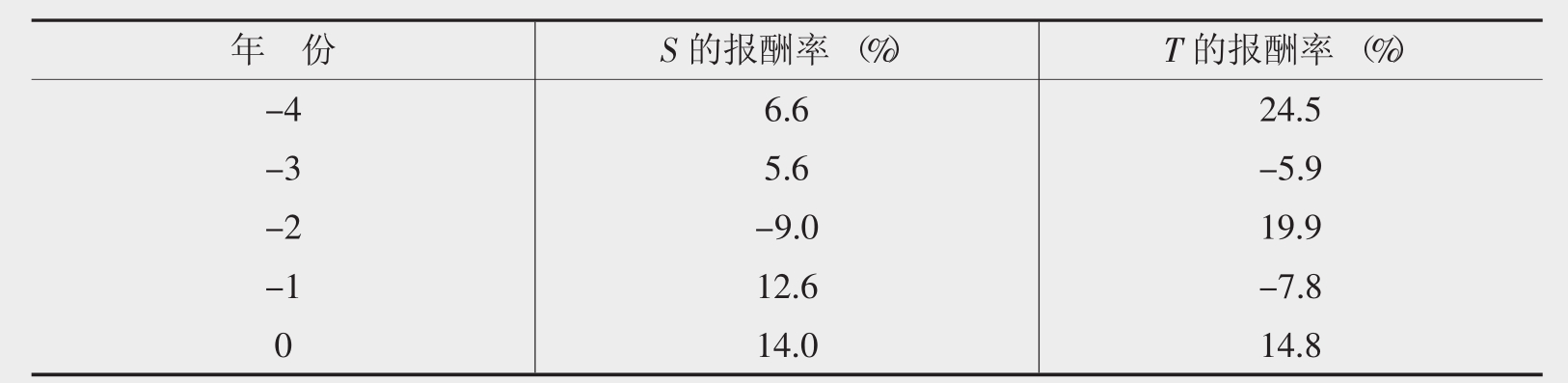
［ （24.5 - 9.10）²+（-5.9 - 9.10）²+（19.9 - 9.10）²+（-7.8 - 9.10）²+（14.8 - 9.10）²） /5］^1/2= 13.39%

由此可见，尽管与证券S相比，股票T有较高的平均报酬率，但是报酬率的标准差也比较高。在图9.1中，我们可以看出用图表示的两种股票的期望报酬率的分布情况。与S相比，由于股票T标准差较高，因此有较高的平均报酬率，但是有一条比较扁平的正态分布曲线。

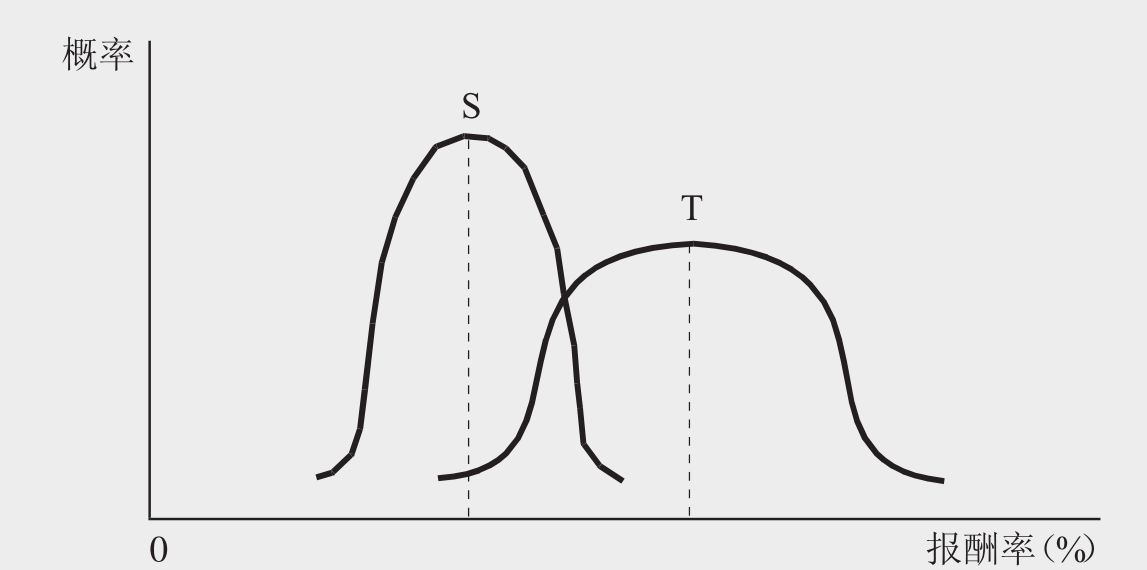
图9.1　股票S与T的报酬率分布曲线