多元化的概念

9.2　多元化的概念

在前面提到投资人为了控制和管理风险，理解他们所面临风险的本质非常重要。公司和投资人所面临的总风险可以分为系统性风险和非系统性风险。系统性风险（也称为不可分散的风险、非特有风险、不可避免风险或者市场风险）指商业周期、政府政策和利息率的变化等系统性因素如何影响股票的报酬率。根据Solnik （1974）的观点，在英国，系统性风险约占个别股票总风险的34%。

非系统性风险（又称为可分散风险，公司特有风险，可避免风险或非市场风险）是指个别股票所特有的风险，例如，个别公司业绩不好或进行清算的风险。尽管在英国，这类风险约占个别股票总风险的66%，但是投资人能够通过增加证券投资的种类有效地降低非系统性风险。Markowitz的投资组合理论基础就是进行股票投资组合能够减少非系统性风险。系统性风险与非系统性风险与证券投资种类的相关性的说明如图9.2所示。

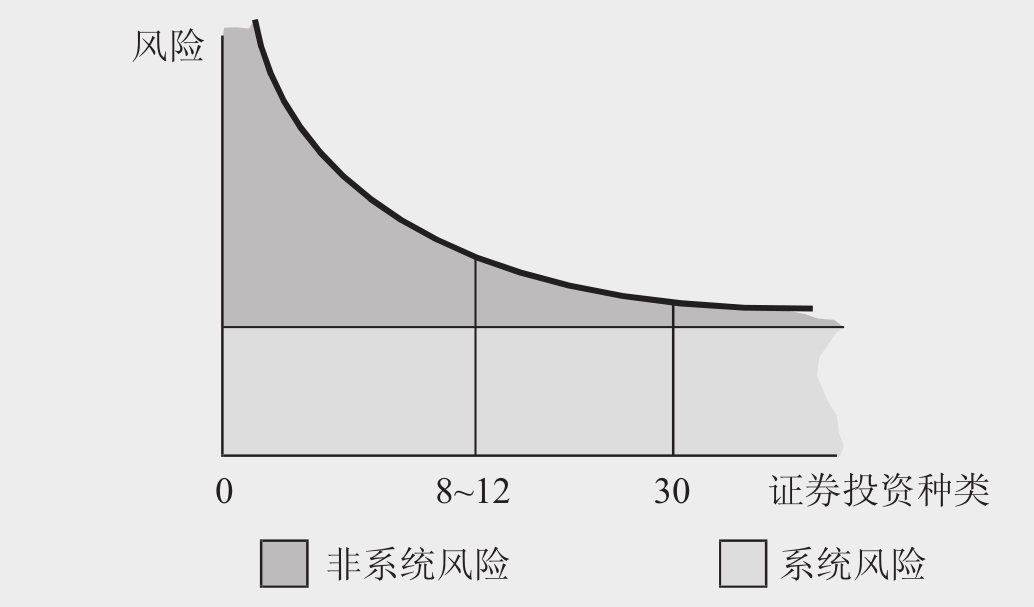
图9.2　非系统风险如何随证券投资种类的增加而被分散

然而，投资人把他们的投资局限于英国的股票没有任何理由。将全世界主要股票交易所的股票进行组合投资的人能够更好地减少非系统性风险。尽管全世界股票交易所的财富是紧密联系的，但是许多交易所之间并不是完全正相关。欧洲和东南亚的股票交易更是如此。Solnik （1974）估计不同国家间的证券投资组合能够将非系统性风险减少到仅占总风险的11%。

9.2.1通过两种股票投资组合分散非系统性风险

最简单的投资组合仅仅包括两种股票。两种股票投资组合减少非系统性风险的程度取决于两种股票报酬率的相关性。相关性通过两种股票报酬率的相关系数（ρ）进行量化，相关系数可以在－1和＋1之间进行变动。

如果ρx， y＝1　　　不能分散任何非系统性风险

如果ρx， y＝－1　　可以分散所有非系统性风险

如果ρx， y＝0　　　两种股票的报酬率之间不相关

因此在挑选两种股票作为投资组合时，选择两种相关系数尽可能接近于－1的股票非常有利。但是，如果相关系数小于＋1，也可以分散部分非系统性风险。在实践中，要找到两种相关系数正好等于－1的证券很难，最常引用的例子是雨伞制造商和冰淇淋公司。

通过下列公式可以计算出股票x和股票y的相关系数ρ_x， y：

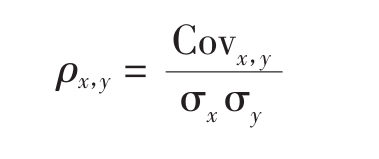
Cov_x，y表示协方差。

如果使用期望报酬率数据，ρ_x， y的计算方法如下：

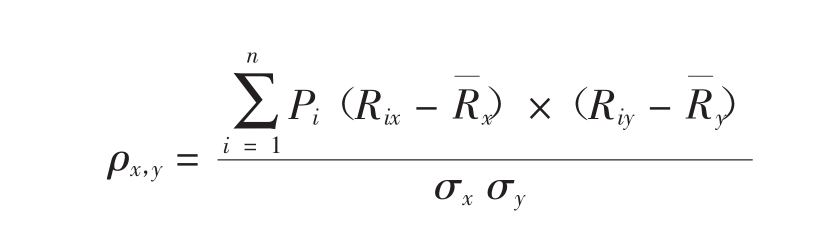
如果使用历史报酬率数据，ρ_x,y的计算方法如下：

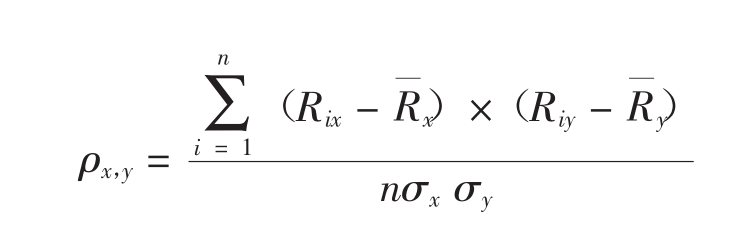
下面给出计算两种股票投资组合报酬率和风险的公式。两种股票投资组合的报酬率是两种股票报酬率的加权平均数。由于分散了所发生的非系统性风险，使得标准差的计算公式更加复杂。

两种股票投资组合的报酬率（R_P） ：

两种股票投资组合的标准差（σ_P） ：

其中，

W_x表示投资于x股票的资金所占的百分比

W_y表示投资于y股票的资金所占的百分比

R_x表示股票x的平均报酬率（百分比）

R_y表示股票y的平均报酬率（百分比）

σ_x＝股票x报酬率的标准差（百分比）

σ_y＝股票y报酬率的标准差（百分比）

ρx_{， y}＝股票x和股票y的报酬率之间的相关系数

σ_p＝包含x和y的投资组合的标准差（百分比）

使用前面例子中的两种股票S和T的年报酬率，可以计算出包含S和T的不同投资比例的一系列投资组合的报酬率和标准差（风险） 。首先，计算出两种股票报酬率之间的相关系数：

ρ_S，T=（（6.6 - 5.96）×（24.5 - 9.10）+（5.6 - 5.96）×（-5.9 - 9.10）+（-9.0 - 5.96）×（19.9 - 9.10）+（12.6 - 5.96）×（-7.8 - 9.10）+（14.0 - 5.96）×（14.8 - 9.10）） / （5 × 8.16 × 13.39）

　　　　　　　　　＝－0.389

80%的S和20%的T的投资组合的风险和报酬率如下：

投资组合的报酬率＝（0.8 × 5.96）＋（0.2 × 9.1）＝6.59%

投资组合的风险＝（（0.8²× 8.16²）+（0.2²× 13.39²）+（2 × 0.8 × 0.2 × 8.16 × 13.39 × -0.389））^1/2

　　　　　　　= 6.02

在表9.3中给出了这些计算结果，各字母含义为：

A表示80% S＋20% T

B表示60% S＋40% T

C表示40% S＋60% T

D表示20% S＋80% T

图9.3中列出了不同的计算结果。由此可见，投资人可以通过确定投资于股票S和股票T的不同比例，把他们的报酬率锁定在弧线SABCDT上的任何位置。这些点比股票S和股票T这两点之间直线上的点要好，这是由于持有多种证券时，所发生的非系统风险被分散了。

表9.3　包含证券S和T的投资组合的风险分散情况

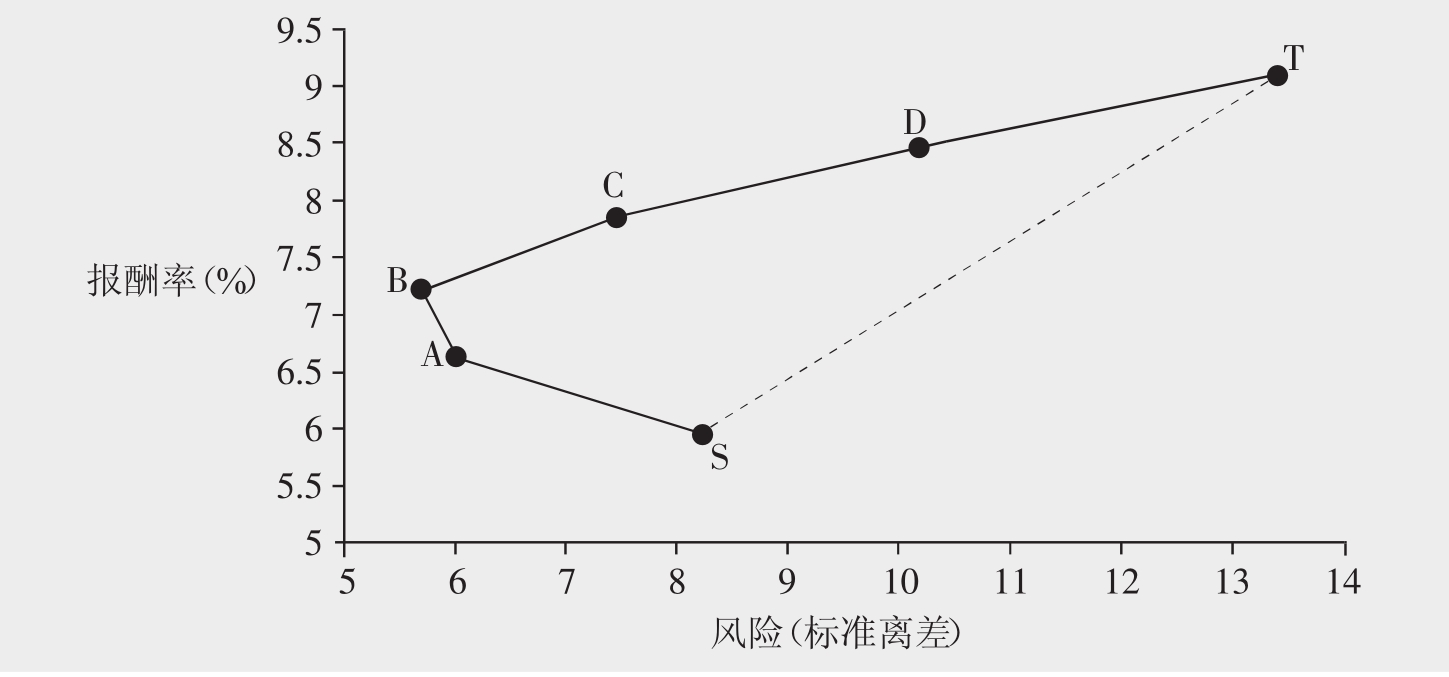
图9.3　证券S与T的不同组合的风险与收益关系图

9.2.2　运用三种股票投资组合分散非系统性风险

在两种股票的投资组合中再增加一种股票，对非系统性风险的分散有进一步的作用。图9.4说明了在前面的例子中加入更高风险和回报率的股票R，各字母含义为：

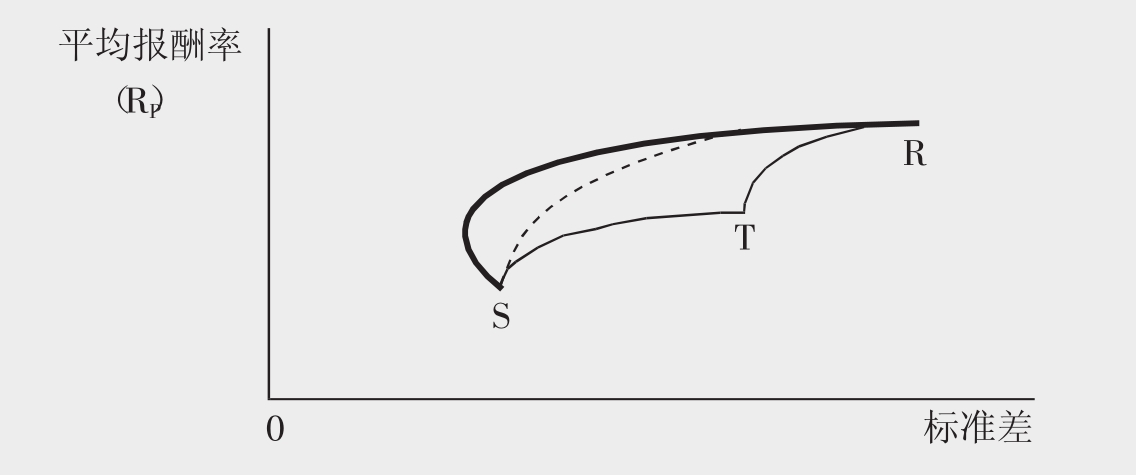
图9.4　由S、T、R三种证券组成的投资组合的风险与报酬图

ST代表证券S和T的投资组合；

SR（虚线）代表证券S和R的投资组合；

TR代表证券T和R的投资组合；

SR（粗线）代表证券T、S和R的投资组合。

由此可见，当投资于三种股票时（也就是粗线SR）可以获得最优投资组合。最优投资组合比仅仅投资于S和T要好，这是因为当投资于三种股票时能够更大程度地分散非系统性风险。投资组合中包含的股票种类越多，越能够分散非系统性风险。这个原理构成了Markowitz的投资组合理论的基础，此时投资者的投资选择并不局限于三种股票，而是包括所有可利用的风险证券。在学习Markowitz的投资组合理论之前，先了解投资人对风险和报酬的态度。