扩展的-模型

针对扩张的S-X模型，我们先给出以下基本假设:

假设1:市场上存在单一的、有限供给的风险资产，伴随由两部分组成的股息变动。第一部分是决定未来股息的基础变量，第二部分属于噪音。累积的股息流Dt满足:

ZD为标准的布朗运动，σD为一个固定的波动参数；基础变量f是不可观测的，但是f满足:

λ≥0是均值回复参数，f是f的长期均值，σf是一个固定的波动参数，Zf为标准的布朗运动。

假设2:市场上存在3类信息:有关股息变动的信息D，其余与基础变量f有关的信号s A和信号s B。交易者通过此3类信息推断当前f值以对资产进行估值。信号向量s A与s B满足:

其中ZA与ZB属于标准的布朗运动，并且ZD、Zf、ZA与ZB这4个过程是相互独立的。

假设3:市场上存在两类风险中性的交易者:A类交易者和B类交易者。两类交易者对有关股息的信息D存在共识，在信号s A和信号s B上存在观点差异。A类交易者偏好信号s A，B类交易者偏好信号s B，并且双方都明白这种分歧的存在。

假设4:当前市场为完全竞争市场，每一类交易者均以其保留价格评估资产。

假设5:交易者能够以同样的无风险利率r进行借贷。

假设6:不存在风险资产的卖空。

在初始的高斯分布条件下，C∈{A，B}类交易者对资产基础价值评估的条件信念服从均值为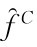，方差为γC的正态分布，这里信念表示对资产基础价值的评估。下面我们刻画固定的解，根据Rogers和Williams(1987)中的VI.9部分:

A类交易者的信念，即对资产基础价值的评估的条件均值满足:

因为f是均值回复的，条件信念也是均值回复的。其余3项代表3类信息来源的冲击影响。这些影响能够以对A类交易者而言的相互独立的标准维纳过程来表示:

类似的，B类交易者的信念，其条件均值满足:

这些影响能够以仅对于B类交易者而言的相互独立的标准维纳过程来表示:

进入流通交易过程之后，股票资产的流动性属性带来了自由买卖的灵活性，流动性资产赋予持有者一种未来时间的选择权，使其能够在不确定性环境中相机抉择出售资产以把握潜在的获利时机。对于资产持有者而言，当出现市场上涨的有利情形，可以适时出售资产以获利；当出现市场下跌的不利情形，可以及时出售资产以止损。因此，下文将分别讨论这两种情形中的交易均衡与相应转售期权的价值。

4.2.1 第一种情形:过度自信、预期获利

当不确定性表现出“有利”的一面时，这种未来时间的选择权便提供给资产持有者在市场上涨情形中适时出售资产以获利的机会。在S-X模型所刻画的资产价格持续上涨的情形中，过度自信的投资者对于流动性资产的需求价格由两部分组成:资产的基础价值以及转售期权的价值。转售期权的价值来自持有者预期能够在将来时点以另一类交易者的更高的需求价格售出资产而带来的收益。此时的转售期权可称之为“获利期权”，S-X模型正是描述了这样一种情形。

在已有的研究文献中，一般采用夸大信号的精确性来对过度自信建模的标准做法。A(B)类交易者把s A(s B)作为他们的自有信号，尽管他们也能够观测到s B(s A)，对资产基础价值评估的差异产生于每一个交易者所认为的自有信号的精确度超过了实际的精确度。A(B)类交易者认为信号s A(s B)的随机波动程度为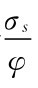，而不是σs，φ≥1测量了过度自信的程度。

交易者对资产基础价值的评估简称为“信念”，两类交易者对资产基础价值评估的差别简称为“信念差异”。以信念的条件均值来代表各类交易者的信念，并以g A、g B表示信念差异:

A类交易者心中信念差异g A的动态过程正确地刻画了他们的过度自信:

其中，

类似的，g B满足:

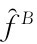是一个对B类交易者而言的标准维纳过程，并且独立于的变动。

不同类交易者之间信念差异的变动将导致交易发生，可以预期对于未来股息前景更为乐观的交易者将为资产出价并且最终持有总的有限的资产。在任一时刻t，C=A，B类交易者愿意为一单位资产出价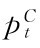，交易者所愿意支付的价格反映了他的基础估值，以及他或许能够在将来时点以另一类交易者的需求价格售出资产从而带来利润的事实。在模型设定中，交易是有成本的——卖方为每单位资产的出售支付C。从而得到均衡价格方程为:

其中，o∈{A，B}表示当前持有者的类别，o表示另一类交易者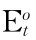，表示O类成员基于t时刻信息的期望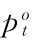；为当前资产持有者的需求价格；q()为转售期权的价值，且满足q＞0，q′＞0。

均衡价格方程表明资产价格由两部分组成:第一部分为持有者的基本估值，由资产的当前持有者对其未来股息流的预期现值构成，以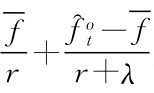来表示；第二部分为资产持有者所拥有的自由选择该资产再次出售的权利的价值，也可以看作是资产本身所包含的一种转售期权的价值，以q()来表示，其价值的大小取决于当前两类交易者的信念差异，即当前两类交易者对资产基础价值评估的差别。

要表明式(4-20)形式的均衡存在，构造一个满足方程式(4-21)的期权价值函数是充分和必要的。最终得到均衡的期权价值函数为:

其中，函数h在区间(-∞，k*)必须严格为正并且递增，在R中严格为正并且满足其具体表达式为:

其中，Γ(·)为Gamma函数，M:R3→R以及U:R3→R为Kummer函数。

k*为产生交易的观点差异的最小量，并且k*＞0。因为函数q在点k*处连续并且连续可导:

由式(4-24)和式(4-25)可知:

以及k*满足:

[k*-c(r+λ)](h′(k*)+h′(-k*)-h(k*)+h(-k*))=0(427)

对应于每一个c，存在唯一的k*为式(4-27)的解，如果c=0，则k*=0；如果c＞0，则k*＞c(r+λ)。并且，有一个唯一的β1为式(4-26)的解。因此，光滑条件足以完全决定函数q与交易点k*。上面构造的函数q是一个均衡的期权价值函数。如果go＞k*，最优策略由立即执行构成；否则等待，直到go≥k*第一次出现。部分详细推导过程见(Scheinkman和Xiong，2003)

4.2.2 第二种情形:信心不足、预期止损

资产的流动性赋予了投资者可以在未来时间内在不确定性条件下行使选择权的可能，因此并非提供仅能在市场上涨情形中适时出售资产以获利的机会。当不确定性表现出“坏”的一面时，这种未来时间的选择权还带给资产持有者在市场下跌情形中及时出售资产以止损的机会。如果资产价格上涨，持有者将有机会出售资产以获利，可以称之为“获利期权”；如果市场持续下跌，持有者将有机会出售资产以止损，可以称之为“止损期权”。总之，资产的流动性使得持有者能够相机抉择做出正确反应。第一种情形描述了市场上涨过程中，过度自信的投资者形成的交易均衡与相应获利期权的价值。本小节将刻画市场下跌过程中，信心不足的投资者形成的交易均衡与相应止损期权的价值。

在市场下跌的情形中，投资者往往是信心不足的，投资获利的预期极易发生变化，最终转变为出售资产以止损，此时，流动性资产所蕴含的转售期权(止损期权)类似于实物期权领域中的放弃期权——如果市场条件变坏，则投资者有权放弃对项目的继续投资，以控制继续投资的可能损失。下面将借鉴S-X模型的数理推导方法求解止损期权的价值。

1)信念差异的动态变化

借鉴通过夸大信号精确性来对过度自信建模的标准做法，在市场下跌的情形中，交易者的信心不足也可以通过对自有信号或自有知识精确性的错误判断来建模分析。A(B)类交易者把s A(s B)作为他们的自有信号，认为信号s A(s B)的波动率为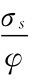，而不是σs，0＜φ＜1测量了信心不足的程度。在这种情况下，对资产基础价值评估的差异即信念差异产生于每一个交易者所认为的自有信号的精确度低于实际的精确度，相对于另一类信号中的噪音，交易者夸大了自有信号中的噪音。或者说，交易者知道他们自有信号的正确的波动程度，进行决策时却使用了错误的权重，对他们的自有信号赋予了过少的权重。

既然所有交易者对资产基础价值评估的信念都具有不变的方差(见式4 5)，可用信念的条件均值表示交易者不同的信念，并以g A、g B表示两类交易者对资产基础价值评估的差异，信念差异如式(4-14)和式(4-15)。

相对于另一类信号中的噪音，A类交易者夸大了自有信号中的噪音，他们的更新规则反映了其对于自有信号s A的信心不足。随着时间的过去，他们期望未来的股息将能够反映信号s A的更多的内容，但市场不涨反跌时，信心不足的A类交易者的预期极易发生变化，其信念将朝着B类交易者的信念进行均值回复。信心不足的存在具有两种效果:一方面，它使得每一个交易者相信，即使今天信念的差异是负的，将来或许会成为正的；另一方面，它加快了信念差异的均值回复。下面的命题1正规地陈述了这一性质:

其中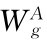，是一个对A类交易者而言的标准维纳过程，并且独立于 的变动。

A类交易者心中信念差异g A的动态过程正确地刻画了他们的信心不足。一方面，信心不足的存在使得σg＞0，A类交易者认为自身对信号s A赋予过多的权重，对于信号s B赋予过少的权重，这导致了伴随股息与信号中的信息流入，信念差异随之变动。另一方面，较小的φ带来一个信念差异更快地进行均值回复的预测。

类似的，g B满足:

其中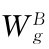是一个对B类交易者而言的标准维纳过程，并且独立于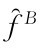的变动。

2)交易均衡

在股票市场中，每个交易者对资产基础价值评估的信念处于不断地变化之中，不同类型交易者之间信念差异的变动将导致交易发生。可以预期，在市场下跌的情形中，对于未来股息前景相对乐观的交易者将为资产出价并最终持有总的有限的资产。设定交易是有成本的，卖方为每单位资产的出售支付c，这一成本代表了交易的实际成本。在任一时刻t，C=A，B类交易者愿意为一单位资产出价，这一价格反映了他的基础估值，以及将来市场表现与预期相反、不升反跌的情况下，他能够以另一类交易者的需求价格售出资产从而限制损失的事实。以o∈{A，B}表示当前持有者的类别，表示另一类交易者，表示o类成员基于t时刻拥有信息的期望值，那么:

其中，τ是一个停时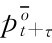，τ是t+τ交易时刻的买者的保留价格，注意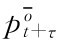-代表了卖方的交易利润。因为，使用信念的条件均值演变的方程(上述式46、式410)可得:

为了刻画均衡，首先为均衡价格方程(434)假定一个特殊的形式。基于均衡价格函数所应满足的性质，我们构造了一个满足这些性质的形式简单并且具有启发性的函数式(4-35)，并证明事实上生成了一种均衡。既然所有相关随机过程都是齐次的马尔可夫过程，交易者都是风险中性的，很自然的寻找到一种均衡，其中，当前资产持有者的需求价格满足:

其中，q＞0，q′＞0。与预期获利的情形类似，此方程表明资产价格由两部分组成:第一部分为持有者的基本估值；第二部分可以视为资产本身所包含的一种转售期权的价值，其大小取决于当前两类交易者对资产基础价值评估的差别。在资产价格上涨的获利情形中，转售期权的价值来自于最优时刻出售资产所获交易利润，不同的是，此处转售期权的价值来自于下跌行情中及时止损所对应的交易利润。

运用式(4-35)来评估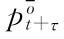，并汇集各项，可以将资产当前持有者所面对的停时问题、式(4-34)重写为:

转售期权的价值满足:

要表明式(4-35)形式的均衡存在，构造满足式(4-37a)的一个期权价值函数是充分和必要的。资产的当前持有者选择一个最优停时来执行他的转售期权，选择最优时点出售资产使得预期收益(止损部分)、交易利润最大，则相应转售期权价值最大，二者是一致的。

3)求解均衡的期权价值函数

从直观上讲，期权的价值q(x)应该至少等于立即出售所实现的收益。期权价值等于立即售出收益的区域为停时区域，剩下的是连续区域，期权的现值应该是连续区域中的一个局部鞅，并且是停时区域中的一个局部上鞅，这些条件可以表述为:

如果式(4-38)的等号成立，则式(4-39a)的等号成立:

此外，函数q应该是连续可导的(光滑的)，我们将得到满足式(4-38)和(4-39a)的一个光滑的函数q，然后使用这些性质并对q施加一个增长条件，来表明实际上函数q是方程(4-37a)的解。

为构造函数q，我们猜测连续区域为区间(-∞，k*），并且k*＞0。k*是产生交易的信念差异的最小量。通常，首先检验q必须满足的二阶普通微分方程，虽然仅仅在连续区域:

下面的命题2帮助我们构造式(4-40a)的一个直接的解。

命题2:

令

其中，Γ(·)为Gamma函数，M:R3→R以及U:R3→R为两个Kummer (超级)函数。h(x)在x=0点连续可导，值为:

那么，式(4-40a)的任何在区间(-∞，0）严格为正并且递增的解u(x)，一定是下面的形式:u(x)=β1h(x)并且β1＞0。

下面的引理1概述了函数h的性质。

引理1:在区间(-∞，0）严格为正并且递增的函数h，在R中严格为正并且满足

既然函数h在区间(-∞，k*）必须严格为正并且递增，从命题2以及引理1可知:

因为函数q在点k*处连续并且连续可导:

这些方程表明:

以及k*满足:

[k*-c(r+λ)](h′(k*)+h′(-k*)）-h(k*)+h(-k*)=0(4-47)

下面的定理1表明:对应于每一个c存在唯一的k*，为式(4-47)的解，并有一个唯一的β1为式(4-46)的解，因此，光滑条件足以完全决定函数q与交易点k*。

定理1:对于每一个交易成本c≥0，都存在唯一的k*与其相对应，为式(4-47)的解。如果c=0，则k*=0；如果c＞0，则k*＞c(r+λ)。

下面的定理2表明，实际上q为式(4-37a)的解。证明由两部分组成，首先，表明式(4-38)与(4-39a)成立，并且q′是有界的。然后，进行标准的论证(例如:Scheinkman和Zariphopoulou(2011)文中有相似的论证)来表明q必定为式(4-37a)的解。

定理2:上面构造的函数q是一个均衡的期权价值函数。如果go＞k*，最优策略由立即执行构成；否则等待，直到go≥k*第一次出现。

4)均衡期权价值的变化过程

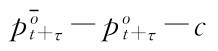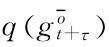转售期权的价值是其期望收益的贴现值，即资产持有者出售资产所获交易利润的贴现值。在期权执行时刻，当前资产持有者所获收益可分解为3个部分:新的购买者所具有的对于资产基本价值评估的超额数量，以及新购买者所认为的转售期权的价值，减去执行期权的成本c(即交易成本)。

这种流动性资产本身所包含的转售期权的价值，其大小取决于当前两类交易者对资产基础价值评估的差异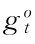，那么，随着交易者之间信念差异的不断变化，转售期权的价值始终处于一种动态变化过程。下面以均衡期权价值函数为例，阐述具体的交易过程中，当信念差异在区间[-k*，k*]单调递增时，均衡期权价值的变化过程。

表4-1 具体交易过程的描述

注:交易价格由两部分构成，即交易时刻购买者对于资产基础价值的评估以及购买者所认为的转售期权的价值qo(-k*)，o∈ ，B{A }表示购买者的类别。

其中，q A、q B遵循一个相同的期权价值函数，即交易者具有最佳交易策略所对应的均衡的期权价值函数:

从当前交易时刻t至下一交易时刻t+τ，包含两个变化过程:

第一，两类交易者在对资产基础价值评估变化过程中产生的信念差异的变化，信念差异x∈[-k*，k*]且单调递增，从而导致交易产生。

第二，转售期权价值q(x)的变动依赖于信念差异的变化过程。交易利润是转售期权价值的来源，交易利润的现值最大化对应均衡的期权价值函数q(x)。信念差异x在区间[-k*，k*]单调递增的过程中，预期交易利润(期望收益)的现值逐渐增大，即期权价值q(x)逐渐增大，至下一交易时刻，期权价值q(x)增至最大，对应即刻出售资产所获交易利润。

表4-2 各交易时刻两类交易者信念及信念差异的变化

对于资产持有者而言，自购入资产至售出的整个持有期间，转售期权价值的变化过程为:

(1)在买入时刻t，支付q(-k*)，为整个持有期间转售期权价值的最小值。

(2)持有期间 ，t+τ[t ]，转售期权价值q(x)始终为正且递增。

(3)出售资产时刻t+τ，即执行期权时刻，转售期权价值增至最大，对应于此刻执行所获交易利润。

综上所述，扩展的S-X模型刻画了两种市场情形中的交易均衡与转售期权的价值，通过对信心系数φ的扩展，给出了统一的均衡期权价值函数。当不确定性出现“有利”的一面时，在市场上涨的情形中，投资者过度自信系数φ∈1，∞( ），资产持有者可以通过行使获利期权而获取收益；而当不确定性出现“坏”的一面时，在市场下跌的情形中，投资者往往信心不足，信心系数φ∈ (0，1 ），资产持有者可以通过行使止损期权而限制损失。