信贷歧视的进一步分析

关于信贷服务的排斥问题，许多学者提出这种基于违约概率进而是“信用分值”的决策方法存在一定的“统计歧视”（statistical discrimination）问题（Phelps，1972；Stiglitz ＆ Weiss，1981；Yinger，1994）。该统计歧视，不仅仅只是基于信息的无完全从而做出的服从以往数据结果的决策，而且在一定程度上也会带有一定的主观偏见，从而对于弱势群体产生了一定的社会排斥性。

本部分内容将在上述分析的基础上，进行进一步的扩展，对信贷服务的歧视问题进行分析，以期更好地解释金融排斥产生的原因。

为研究方便起见，假设有两个群体，强势群体和弱势群体，划分的标准可以是多种，例如根据核心和边缘地区进行区分，根据所属的居住地区进行区分，根据是否是属于少数民族进行划分，等等。

当银行在现有的信息基础上无法对各申请者进行违约风险评估时，也就是根据信用评分标准处于“中间的信用分值段”，将带有一定的偏见性，即会主观认为弱势群体的申请者要比强势群体有更大的违约可能性；当然，在较高的信用分值段和较低的信用分值段，银行都能容易地进行客观地评价，便也不存在这种歧视性问题了。

本分析将在借鉴Calem＆Stutzer（1995）的研究思路基础上，对信贷服务排斥所伴随的歧视问题进行分析。

假设一家庭需要融资1单位进行购房，该房价值为V，为此向银行申请贷款，其在第二期需要向银行支付的本息为R，且满足V ＞＞ R。设该家庭第二期收入服从如下分布：

也就是说，如果其一旦实现收入大于0，便会归还贷款，并不存在主动的违约行为。

现假设有两类风险特征的申请者，一是高风险型申请者，以H表示，其获得收入y的概率为MH，二是低风险型申请者，以L表示，其获得收入为y的概率为ML，并有MH＜ ML。同时，假设P为个人特质变量、宏观和制度环境、以及银行获取信息等的障碍函数，即有Mi＝M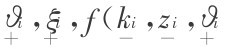（））（i＝H，L，下同）。

银行对i风险类型的申请者审核通过的概率为ηi。如果申请者申请到了贷款，但在第二期没有收入，此时银行会组织清算，最终导致该申请者潜在损失了φi。在其他条件不变情况下，法制环境越好（例如执法效率较高）、社会契约意识越浓等宏观环境越好，则导致申请人潜在损失的就越少，即φi＝φ（ξi－）。

若银行未贷款给申请者，则假设该申请着仍有δi的收益，该变量也可看成是通过其他渠道等筹集资金所获得的净收益、或是从是其他活动所获得的收益，根据假设有δi＜ V －Ri。

假设在某一信用分值区间的群体中，弱势群体所占的比例为τ，其中高风险类型的占βr；强势群体所占的比例为（1－τ），其中高风险类型的占βq，因此，总人群中高风险所占的比例为：β＝τβr＋（1－τ）βq。

根据信贷的统计歧视观点，显然有：βr＞＞βq。

所以，该申请者有如下的效用函数：

Uij＝ηjMi（V＋y－Rj）＋ηj（1－Mi）（V－φi）＋（1－ηj）（Miy＋δi）＝ ηj（V－MiRj－φi＋Miφi）＋Miy＋δi（1－ηj）

根据“自我选择”性，有Uii≥ Uij，i，j＝ H，L。

Uij满足连续、可导的条件，所以有：

故：φi－Rj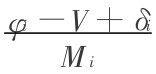＝i

假设φL＝ φH，因为RH＞ RL，所以有：

因为MH＜ ML，所以有：δH＜＜ δL。

而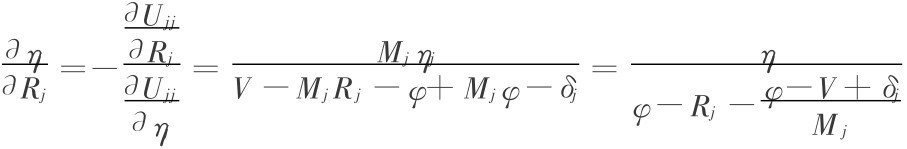

由于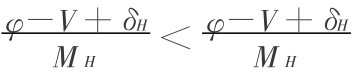，所以在ηH＝ηL，RH＝RL条件下，有：

也就是说，H风险类型的无差异曲线将在某一点之后处于L风险类型的无差异曲线下端，如图6．3所示。

现在首先考虑无歧视情况下的均衡。

根据瓦尔拉斯定义，完全竞争条件下，满足：MiRi－1＝ 0

也就是，（βMH＋（1－β）ML）Rβ－1＝0，且β＝τβr＋（1－τ）βq

当β充分小时，由于MH＜ ML，以及MH≤（βMH＋（1－β）ML）≤ML，所以Rβ也较小，其取值范围为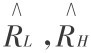（），且较接近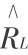，如图6．3中A点。

此时，对于H风险类型，在A点和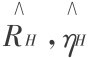（＝1）之间进行选择的话，会偏好于A点；对于L风险类型，在A点和（）之间进行选择的话，也会选择A点。因此，点A为H和L风险类型的共同均衡点，且在该点，获得贷款的概率均为1。也就是说，并不存在对弱势群体的歧视问题。

图6．3 信贷歧视的无差异图

现引入歧视问题，即考虑分离均衡情况。

根据上述式子，当β较大、接近于1时，Rβ增加，处于类似于C点位置，此时，H风险类型会偏好A点，而L风险类型会偏好（），因此出现了分离均衡的状态。

进一步考虑强势和弱势两个群体，当β＝τβ＋（1－τ）β时，若β充分小，于是，βq＜β＜βr，代入（βMH＋（1－β）ML）Rβ－1＝0中，可以得到：Rqβ＜Rβ＜ Rrβ，若βr充分大时，Rrβ在（R0，1）的右边，如C点位置，因此Rqβ，Rβ，Rrβ分别对应B、A、C点。

此时，对于强势群体而言，无论是H风险类型，还是L风险类型，其均衡点均为B点；而对于弱势群体而言，若为H风险类型，则会偏好于C点，若为L风险类型，则会偏好于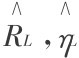（）点，所以便出现了歧视。∧

根据图6．3，UHH＝UHL，对于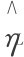的求解如下：

因此

因为，所以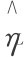＜ 1，故存在一定的歧视问题，即对于弱势群体而言，L风险型的申请者被拒绝的概率比较大。

进一步

因此，随着MH（））的增加，也增加，而随着φH（ξi－）的增加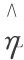，反而减少，见图6．4的模拟结果。

图6．4 左图为MH与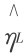的关系，右图为ΦH与η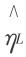的关系

注释：左图中，各参数值为：V＝5，δH＝1，φH＝2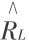，＝1．25；右图中，各参数为：V＝5，δH＝1，MH＝0．3，＝ 1．25。

据此，提出如下假设：

H3－1：随着人均收入等个人特质变量的提高，弱势群体被排斥的可能性减少；

H3－2：随着法律制度、社会资本等宏观环境的提高，弱势群体被排斥的可能性也减少；

H3－3：随着接触距离的增加，弱势群体被排斥的可能性增加；

H3－4：随着“自我排斥”的增加，弱势群体被排斥的可能性增加。