(一)单指数模型的结构和特征
1.单指数模型的结构
单指数模型由威廉·夏普(Sharpe)首先提出,其基本思想是认为证券收益率只与一个因素有关。假定每种证券或多或少地受股票市场股价指数的影响。当投资者观察证券市场,可以发现,当股价指数上涨时,大部分股票的价格也上涨;当股价指数下跌时,大部分股票的价格也下跌。这说明,各种证券对市场变化有共同的反应。因此,可以用一种证券的收益率和股票市场股价指数的收益率的相关关系得出以下模型:
式中,Ri代表第i种证券的收益率; 代表股票市场股价指数收益率;A代表证券收益率中独立于市场的部分;β代表证券收益率对股价指数收益率的敏感程度,也即测度
代表股票市场股价指数收益率;A代表证券收益率中独立于市场的部分;β代表证券收益率对股价指数收益率的敏感程度,也即测度 既定变化情况下Ri预期变化的常数;εi代表剩余收益率,它是一个随机变量,测度
既定变化情况下Ri预期变化的常数;εi代表剩余收益率,它是一个随机变量,测度 与平均收益率之间的偏差。
与平均收益率之间的偏差。
单指数模型假设两种类型的因素造成证券收益率各个时期之间的差异:(1)宏观经济环境的变化,如通货膨胀率、存款利率的变化等。宏观经济变化会影响市场股价指数的变化,并通过市场驱动影响到每个证券收益率的变化。如图7.25所示,在一定时间内,股价指数收益率为-5%,则证券的收益率可为2%;如果股价指数的收益率为15%,则证券收益率可为10%。可见,证券的不同预期收益率是市场不同时期不同影响所形成的。(2)微观因素的影响,具体表现为股份公司内部环境的变化,如新产品的开发、公司内部的人事变动等,它只对个别证券产生影响,而没有普遍作用。在一定时间内,在股价指数一定的条件下,微观因素的影响能使证券收益率高于或低于正常水平,在(7-26)式中,它引起A和εi的变动,也是产生残差(εi)的主要原因。这里,我们假设微观因素的变动对其他证券没有影响。
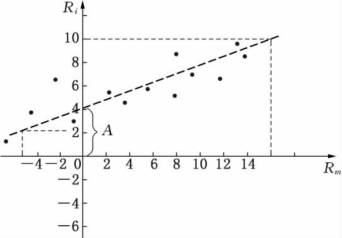
图7.25 模型的特征线
需要指出,其他类型的影响因素在(7-26)式中不予考虑。它们可能是行业因素,某一事件常对某一行业的许多公司有影响,但还不至于广泛地足以影响经济系统或整个证券市场的股价指数。这类因素也常引起残差,而单指数模型假定残差均由微观因素引起。
单指数模型中有以下两个基本假设:
这一假设使单指数模型同其他用以描述协方差结构的模型区别开来了。它意味着各种证券有规则地一起变动的唯一理由是它们同市场一起变动,而可以解释各种证券一起变动的市场以外的影响(如产业影响)是不存在的。显然,对于单指数模型来说,这个假设是十分重要的,模型的性能如何,就取决于这个假设对实际的近似程度。
假设二:市场指数和独立的证券收益率不相关,即协方差:
![]()
同时,市场指数收益率的方差为:
![]()
以及剩余收益率的方差为:
![]()
因此,单指数模型中某种证券的预期收益率、方差和协方差可以这样推导出来:
(1)某种证券的预期收益率:
![]()
由于随机变量的期望值等于期望值的和,故:
![]()
又由于A和β都是常数,而且εi的期望值E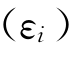 )=0,故:
)=0,故:
![]()
(2)任何证券收益率的方差:
![]()
将(7-28)式代入上式,可得:
根据(7-27)式,可得:
![]()
由于E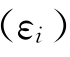 )=0,故:
)=0,故:
![]()
由(7-29)式可知,我们总可以将某种证券收益率的方差分为两部分:系统风险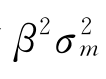 (主要由宏观因素影响产生)和残差方差或者独立风险或非系统风险
(主要由宏观因素影响产生)和残差方差或者独立风险或非系统风险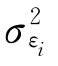 (主要由微观因素影响产生),也就是说,任一证券的风险包含系统风险和非系统风险两种。在单指数模型的假设条件下,
(主要由微观因素影响产生),也就是说,任一证券的风险包含系统风险和非系统风险两种。在单指数模型的假设条件下,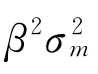 反映了不能分散掉的风险
反映了不能分散掉的风险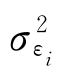 表示投资者只要通过分散化投资就可以消除这项风险。
表示投资者只要通过分散化投资就可以消除这项风险。
(3)任何两种证券间的协方差:

根据假设,最后三项等于0,因此:
![]()
由上式可知,协方差只取决于市场风险。
例如,假设股票收益率和市场股票指数收益率如表7.13所示。
表7.13 单指数模型中的数据

利用(7-28)式、(7-29)式和(7-30)式以及表7.13的数据,可算得:

因此,表7.13中,设β=1.5,则第(5)栏 的值可由第(2)栏乘上1.5求得。
的值可由第(2)栏乘上1.5求得。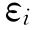 的期望值等于0,所以
的期望值等于0,所以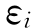 的和也等于0。5个月的收益是40,其中30与市场相关,所以独立部分A的和等于10。因为A是常数,所以每个月的A=10/5=2。剩下的
的和也等于0。5个月的收益是40,其中30与市场相关,所以独立部分A的和等于10。因为A是常数,所以每个月的A=10/5=2。剩下的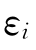 就是能使单指数模型等式两侧相等的数值,如表7.13中的第(6)栏所示。由此可见,单指数模型中所有的值都来自β。β把收益分为与市场相关和与市场独立两部分。当β确定为1.5时,市场收益率独立于剩余收益率
就是能使单指数模型等式两侧相等的数值,如表7.13中的第(6)栏所示。由此可见,单指数模型中所有的值都来自β。β把收益分为与市场相关和与市场独立两部分。当β确定为1.5时,市场收益率独立于剩余收益率 。β的值取得低,部分市场收益就进入
。β的值取得低,部分市场收益就进入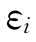 ,
, 与市场收益率的协方差取正值。β的值取得高,市场收益去掉太多,就会导致
与市场收益率的协方差取正值。β的值取得高,市场收益去掉太多,就会导致 与市场的协方差取负值。因此,β值恰好就是把市场收益与独立收益分离开。
与市场的协方差取负值。因此,β值恰好就是把市场收益与独立收益分离开。
如果一种证券的单指数模型成立,那么证券组合的预期收益率为:
![]()
式中,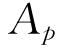 、
、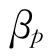 分别是
分别是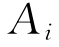 和
和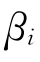 的加权平均,即:
的加权平均,即:
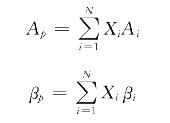
则(7-31)式又可以写成:
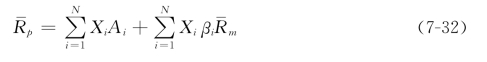
式中,Xi为证券组合中各种证券所占的投资比例,即权数。而证券组合的方差可以写成:
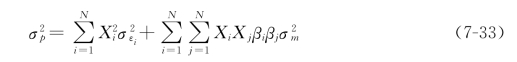
由(7-32)式和(7-33)式可知,如果我们估计出每种股票的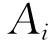 和
和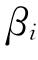 、
、 以及市场预期收益率
以及市场预期收益率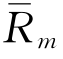 和方差
和方差 ,我们就能估计出任何证券组合的预期收益率和方差。因此,这时需要估计的值有3N+2个了。这较之于马柯维茨方法选择最佳证券组合是大大地简化了。目前,西方国家的绝大多数金融机构都跟踪150~250种股票,若用马柯维茨方法,就必须估计150~250个预期收益率数据,150~250个方差数据,以及11 175到31 125个相关系数数据。对单指数模型来说,只需估计452~752个数据就可以了,这比11 175~31 125个数据值要少多了。而且,现在也不需要直接估计证券的联合变动,而只要估计每种证券与市场一起变动的情况就可以了。
,我们就能估计出任何证券组合的预期收益率和方差。因此,这时需要估计的值有3N+2个了。这较之于马柯维茨方法选择最佳证券组合是大大地简化了。目前,西方国家的绝大多数金融机构都跟踪150~250种股票,若用马柯维茨方法,就必须估计150~250个预期收益率数据,150~250个方差数据,以及11 175到31 125个相关系数数据。对单指数模型来说,只需估计452~752个数据就可以了,这比11 175~31 125个数据值要少多了。而且,现在也不需要直接估计证券的联合变动,而只要估计每种证券与市场一起变动的情况就可以了。
2.单指数模型的特征
前面已经指出,βp为证券组合中每种证券的βi值的加权平均值,其权数为证券组合中每种证券的投资比例,即:
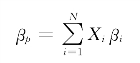
同样,证券组合的Ap为:

从而可写成:
![]()
由上式可知,对于任何确定的 ,只要Ap=0和βp=1,就可使
,只要Ap=0和βp=1,就可使 =Ap+βp
=Ap+βp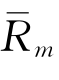 。βp可用来检验市场风险对某种证券的影响程度。如果某种股票的风险程度与整个市场的风险程度一致,那么这种股票的βp等于1;如果某种股票的βp大于1或小于1,则说明该股票的风险程度高于或低于整个市场水平。如某一股票的β为0.73,这就意味着当整个股票市场价格涨到1时,该股票价格上涨0.73。这个数字说明,这种股票价格反应比整个市场趋势慢,即其波动幅度比整个市场小,风险程度小于整个市场水平。
。βp可用来检验市场风险对某种证券的影响程度。如果某种股票的风险程度与整个市场的风险程度一致,那么这种股票的βp等于1;如果某种股票的βp大于1或小于1,则说明该股票的风险程度高于或低于整个市场水平。如某一股票的β为0.73,这就意味着当整个股票市场价格涨到1时,该股票价格上涨0.73。这个数字说明,这种股票价格反应比整个市场趋势慢,即其波动幅度比整个市场小,风险程度小于整个市场水平。
现在再来看证券组合的方差:
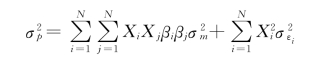
如果上式中的i=j,那么,上式中的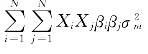 就变成了
就变成了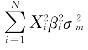 ,因此,上式可变为:
,因此,上式可变为:
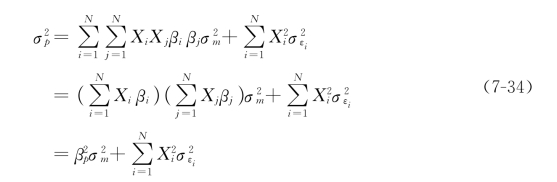
假定投资者将资金等比例地投在证券组合中的每种证券上,那么,(7-34)式就变成:
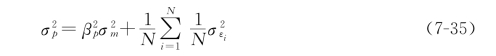
(7-35)式右边第二项![]() 为平均剩余方差,被分母N除后其值随N的增大而趋于零,也就是说,
为平均剩余方差,被分母N除后其值随N的增大而趋于零,也就是说, 对组合风险的影响随组合中所包含的证券种类数增加而变小并趋于零。
对组合风险的影响随组合中所包含的证券种类数增加而变小并趋于零。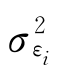 是可分散掉的风险,称为非市场风险或非系统风险,表7.14说明分散化投资对避免非系统风险的作用。
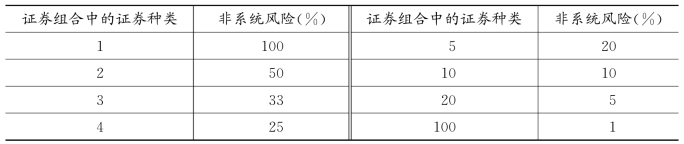
是可分散掉的风险,称为非市场风险或非系统风险,表7.14说明分散化投资对避免非系统风险的作用。
从表7.14中可知,如果假设未经分散处理证券的非系统风险为100%,那么,当把资金分散到5种证券时,非系统风险降为原来的20%,当把资金分散到100种证券时,非系统风险只剩下1%,显然下降幅度非常快。
表7.14 分散化投资对避免非系统风险的作用
但是,与βp相关联的风险,不会随证券组合增大而削减,假设剩余方差或剩余风险趋于零,证券组合的风险就接近:
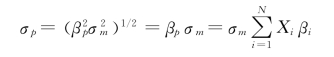
由于σm相同,所以不管考察什么股票,这种股票对证券组合风险的贡献都可以用βi测度。通常把βi称作不可分散风险,或者称为系统风险。这种风险不会因为证券投资分散化而消失。当然,投资者可以通过改变持有股票的投资比例来增加或减少平均系统风险。
【例7-6】 假定4种股票的系统风险分别是β1=0.9,β2=1.6,β3=1.0,β4=0.7。如果这4种股票在证券组合中的比例相等,即Xi各占25%,那么这个证券组合的平均系统风险为:

这个数值稍大于1,说明这个证券组合的波动也比市场的波动稍大。如果投资者把投资比例改为X1=5%,X2=80%,X3=10%,X4=5%,那么上述4种股票构成的一个证券组合的平均系统风险就成为:
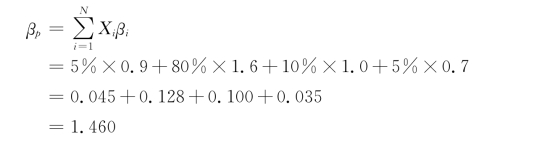
显然,这个证券组合的风险程度比之于1.050更高于市场风险。
(二)β系数的估计和应用
前面我们已知,单个证券的不可分散风险由β系数表达出来,因此对单个证券的β值的估计就是一项必不可少的工作。特别是因为β值纯属理论上假设模型中的参数,实际证券市场数据并不能直接提供它的值,因此,β值不是从实际数据中测出来的,而是要估计出来。
由方程式Ri=A+βRm+εi,利用一组反映个别证券收益率和市场指数收益率的历史数据,根据最小二乘法即可求出β值。也就是说,求出下式的偏导数并令它们等于零,就能得到β系数。
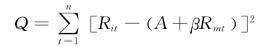
令

A的估计值可以使用下式求得:

举例来说,使用表7.13中的第(1)栏和第(2)栏的数字资料,可以算出这种股票的平均收益率为:
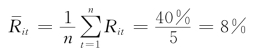
市场的平均收益率为:

其β值为:
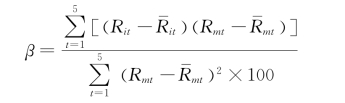
上式的分子:

上式的分母等于:

从而β值为:
![]()
表7.13的单指数模型把β假定为1.5,根据就在这里。
这个例子的A值为:
A=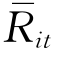 -
-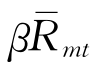 =8-1.5×4%=2%
=8-1.5×4%=2%
事实上,证券的β系数可以看作证券特征线的斜率。加入在一定时期内,此线是固定的,即它在各个时期内不发生变化。对β系数计算的统计程序是简单的线性回归分析,现根据表7.15做出说明。
表7.15 回归分析计算表

根据表7.15的回归分析计算表,可算得如下的数值:
(1)β系数。
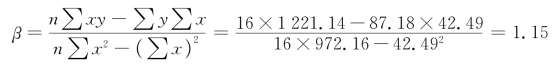
(2)A系数。
![]()
(3)标准误差SE。
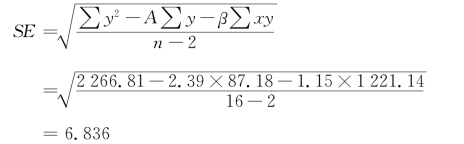
(4)β系数的标准误差。

(5)A系数的标准误差。

(6)相关系数。
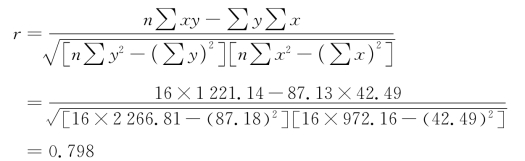
(7)确定系数。
![]()
(8)非确定系数。
![]()
给定A系数和β系数,则该证券估计的特征线为:
![]()
由回归分析得到的A和β值,是股票实际A和β值的估计值。估计是有误差的,如此例中的标准误差为6.836,β系数的标准误差为0.233,A系数的标准误差为1.817。而且,实际的A和β随着时间的推移也会发生变化,因此,根据股份公司情况的变化,也要对它们做适当的调整。但尽管如此,人们还是运用回归分析得到过去的β值来预测未来的β值。同时,需要指出,证券组合的历史β值,能比单个证券的历史β值更好地预测未来的β值。
(三)β系数的调整
为了改善预测能力,需要对过去的β值进行修正。布鲁姆(Blame)的研究表明,预测期的β系数比由历史数据得到的β系数更接近于1,即β系数有一种趋向于1的倾向。
对β系数的调整方法主要有三种。
第一种方法是布鲁姆提出的办法,那就是通过直接测定这种趋向于1的调整来修正过去的β系数,并假定一个时期的调整值是下一时期调整的确切估计。

图7.26 时间水平线
图7.26显示了时间水平线,时间单位为1个月,投资者现在处于t年的最后一个月,要为t+1年的第一个月做出投资计划,那么投资者先要估计历史的β系数,即t年的β系数,这个问题如前所述,然后通过考虑时间过程中β系数的相关程度,对β系数的历史估计值进行调整。
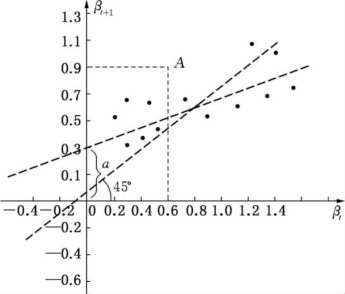
图7.27 β系数相关程度的特征线
图7.27,是t-1年中12个月的β系数和t年中的β系数的相关程度的特征线。如果β系数不随时间发生变化,则t年和t-1年β系数相关程度的特征线应为45°线。实际的观察值并非如此,如图7.27中的A点所示,在t-1年时,其β系数为0.6,在t年时,则为0.9。根据不同的观察值,可得一平均直线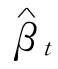 =a+0
=a+0 ,假设系数之间的相关程度的β大小不会因为时间发生变化,则进一步可得:
,假设系数之间的相关程度的β大小不会因为时间发生变化,则进一步可得:
![]()
例如,在图7.27中,假设a0=0.35,a1=0.65,则可以估计出t+1年的β系数:
![]()
这种修正对股票β系数的影响很值得注意。如果在t年的β系数为2,那么预测的β系数就是0.35+0.65×2=1.65,而不是2;如果在t年的β系数为1.5,那么预测的β系数就是0.35+0.65×1.5=1.325,而不是1.5;如果在t年的β系数为0.8,那么预测的β系数就是0.35+0.65×0.8=0.87,而不是0.8;如果在t年的β系数为0.5,那么预测的β系数就是0.35+0.65×0.5=0.675,而不是0.5。可见,这个方程使高的β系数变低,使低的β系数变高,修正的β系数有一种趋向于1的倾向。
同时需要指出,由于这个方程测度的是两个时期β系数的关系,因此,如果这两个时期的平均β系数比第一个时期的平均β系数增加的话,那一定是因为第一个时期的平均β系数增加的缘故。显然,这个性质是不尽如人意的。因此,如果没有理由预期平均β系数具有这种递增趋势的话,我们就应该调整预测的β系数,使得β系数的均值等于历史β系数的均值,以此来改进我们的估计[2]。
对β系数进行修正的第二种方法叫做贝叶斯估计方法,是由瓦锡克(Vasicek)提出的。这种方法不要求所有股票的β系数朝着其均值即β=1的方向调整,而是根据β系数的不同样本误差,对不同股票的β系数做不同的调整。样本误差越大,调整也就越大。其预测公式为:
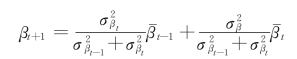
对过去的β系数进行修正的第三种方法是在测算过程中考虑一系列的影响因素。
假设公司规模是影响公司经营的一个重要因素,定义为S,则除了估计βt和St-1的相关关系,可以得到如下的等式:
![]()
同样地,假设β系数和公司规模间的相关程度的大小不随时间发生变化,则进一步可得:
![]()
除了公司规模外,公司利润收入的稳定性、财务杠杆的作用、公司资产的流动性都不同程度地影响β系数的估计值,上述的等式也随之增加相应的变量,等式可写成:
![]()
许多经验研究表明,经过上述三种方法调整的未来β系数预测值,要比未经调整的β系数预测值正确得多。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















