结构化蒙特卡罗法

这一方法也称随机模拟方法（random simulation），其基本思想是利用计算机随机模拟出风险因素的随机价格走势，并以此来近似解释该风险因素的市场特征。这个随机模拟的过程就是重塑投资组合价值分布的过程。

结构化蒙特卡罗法通过近似地模拟风险因素的统计分布来计算潜在的收益和相应的VaR。它要求每个风险因素对应一个其未来的可能分布，如正态分布、对数正态分布、T分布等等，然后利用历史的数据来确定这些分布的参数。利用这些分布和参数，随机产生成千上万种风险因素的未来可能值，在这一场景下再重新确定投资组合的价值。最后利用这些随机产生的组合收益，构造出组合的经验分布，并确定在一定置信水平下的VaR值。

蒙特卡罗模拟可以解决多种类型的问题，视其是否涉及随机过程的形态和结果，蒙特卡罗模拟的应用可以分为两大类。

（一）定性问题

用蒙特卡罗模拟求解这类问题的方法是，首先建立一个与所求解有关的概率模型，所求的解就是所建模型的概率分布或数学期望，然后对这个模型进行随机抽样观察，即产生随机变量，最后用算术平均值作为所求解的近似估计值。

（二）随机问题

对这类问题，虽然有时可表示为多重积分或某些函数方程，并进而可考虑用随机抽样方法求解，然而一般情况下都不采用这种间接模拟方法，而是采用直接模拟方法，即根据实际情况的概率法则进行抽样试验。

基于历史模拟法的VaR计算是基于市场因子的历史实际价格变化得到组合损益的n个可能结果，从而在观测到的损益分布基础上通过分位数计算VaR。基于蒙特卡罗模拟的VaR计算原理与此类似，不同之处在于市场因子的变化不是来自于历史观测值，而是通过随机数模拟得到。其基本思路是重复模拟金融变量的随机过程，使得模拟值包括大部分可能情况，这样通过模拟就可以得到组合价值的整体分布情况，在此基础上就可以求出VaR。

例如，可以模拟10000种情景，从而得到组合价值的10000种可能结果；基于此计算出损益分布，根据最不利的第500个情景（95%的置信水平）或最不利的第100个情景（99%的置信水平）确定VaR的数值。

可按以下步骤运用结构化蒙特卡罗法：

（1）确定风险因素所服从的随机过程及随机参数，其中方差和相关系数等参数可以从历史数据或期权数据中得到。

（2）依次产生相应的伪随机数ε1，ε2，…，εn，并计算得到模拟价格，，…，。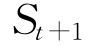

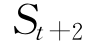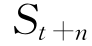（3）根据步骤（2）中得到的模拟价格计算目标时刻t时，投资组合的价值Ft。

（4）重复步骤（2）和步骤（3），如重复K＝10000次，得到一系列的投资组合模拟价值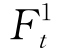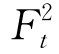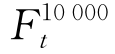，，…，，根据这一系列价格就可以估计出投资组合在t时刻的分布，并利用该分布计算出VaR值。在给定的置信水平c下，VaR值实际就是投资组合价值超过c乘以10000个Ft的部分。

该方法的优点是：结构化蒙特卡罗法是衡量金融风险最全面的数值分析方法。它能处理其他方法所无法处理的风险和问题，如非线性价格风险、波动性风险、肥尾分布、极端事件甚至信用风险，它都能有效地处理。

该方法的缺点如下：

（1）结构化蒙特卡罗法最大的不足就是计算量太大。如果投资组合中有1000种资产，对每种资产的模拟路径为1000种，那么投资组合的价值就会有100万个。如此大的计算量，是以牺牲计算结果的及时性为代价的，所以该方法不适合需要及时提供风险度量度的场合。

（2）结构化蒙特卡罗法的另一缺点是它存在模型风险。因为它依赖于基础风险因素的随机模型及证券的定价模型。如果模型有缺陷，据此得到的VaR也必然不准确。

但不可否认，该方法仍是目前度量市场风险最全面的方法。