模型的扩展类型

（一）ACD模型扩展类型介绍

Engle和Russell（1998）提出的ACD模型激发了实证金融领域里对价格和交易期间关系研究的积极性，例如，Renault和Scaillet（2001）及Giot（2000）提出在价格期间过程模型中把这些方法与期权定价和日内风险管理联系起来。在Engle和Russell（1998）的ACD模型开启了这类分析的开端后，近年来关于ACD模型出现了多种扩展形式。

Bauwens和Giot（2000）用对数ACD模型避免了原始ACD模型的非负约束，这使得市场微观假设的实证变得更容易了，Bauwens和Veredas（1999）提出了随机条件期间过程，依靠一个潜在的随机因子来捕捉市场里没有观察到的随机信息流，Ghysels、Gourieroux和Jasiak（2003）用这种随机期间模型来处理期间过程中的高阶动态性。Zhang、Russell和Tsay（2001）提出了一个建立在自激励门限自回归过程基础上的非线性模型。Dufour和Engle（2000）提出了非线性ACD模型。

在这里我们探讨了ACD模型的不同扩展类型，遵循Hentschel（1995）所用的建立非对称GARCH模型家族的方法。模型参数的嵌套采用了将λ≥0参数定形于条件期间过程的Box-Cox（1964）变量转换，并且考虑了对冲击的非对称反应。Engle和Russell（1998）显示了标准的ACD模型用于金融数据容易导致在极端间隔（非常长或者非常短）后的过度反应，对冲击的非对称反应试图解决这个问题。在ACD的扩展模型里，考虑了充分条件的存在，如高阶动差（higher order moments）、严格稳定、几何变形和具有指数衰减的混合β特性等。尽管对于自相关函数和期间过程动差还没有一般的分析解决办法，但是针对期间过程的λ次幂有可能推导出自协方差函数和动量衰减关系。为了计算出任何一个假定动量和自协方差函数的表达式，首先必须把注意力集中在特别的低阶次上，如：λ→0和λ＝1。

随后我们用中国石化（600028）的价格期间和成交量期间的建模实证，对ACD扩展类型的实际应用不仅可以分析这类模型在中国证券市场的实用性，而且可以弥补简单ACD模型的不足之处，有利于我们采用更好的模型类型进行高频数据的研究工作。ACD扩展类型不仅拒绝了已有模型强加的约束条件，而且证明了考虑凹形冲击影响曲线（concave shocks impact curve）是非常重要的，因为它调节了过度预测短期间的问题，因此在Box-Cox变量转换和非对称效应都可以导致凹形冲击影响曲线时，发现两者之间存在某种替代作用并不令人奇怪。

与前面相同，xi＝ti－ti－1表示在ti和ti－1时刻发生的两次事件的时间间隔，例如，价格期间（price duration）反映了股票价格有一定变化时的时间间隔，成交量期间（volume duration）反映股票成交量有一定变化时的时间间隔，交易期间（trade duration）则表示在两个连续交易之间的时间间隔。为了说明在金融期间数据中序列相关是共同的，Engle和Russell（1998）用公式xi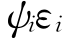＝表示时间过程，条件期间过程ψi＝E（xi｜Ωi－1）为第i个期间持续的期望，Ωi－1包括了时刻ti－1时所有的有用信息集，｛εi｝～i.i.d。如同Hentschel（1995）那样，通过运用Box-Cox变量转换，将参数λ≥0用于条件期间过程ψi，给出表达式（9-13）：

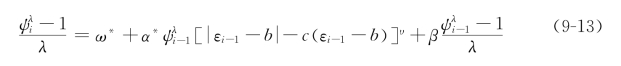
参数λ≤1时，Box-Cox变量转换是凹的；

参数λ≥1时，Box-Cox变量转换是凸的。

将（9-13）式变形推出扩展自回归条件期间模型（EACD），如公式（9-14）：

其中，ω＝λω*－β＋1，α＝λα*。

EACD模型提供了一个弹性函数形式，允许条件期间过程以独特的方式对小的冲击和大的冲击分别做出反应，冲击影响曲线通过转移参数b和旋转参数c合并了非对称的反应。

因为期间是非负的，所以转移参数b对于用冲击影响曲线来反映非对称效应是十分关键的。参数c指出了旋转是顺时针的（c＜0）还是逆时针的（c＞0）。转移和旋转并不一定会相互加强，实际上，转移参数b主要反映小的冲击，而旋转参数c主要反映大的冲击。形态参数υ扮演了与λ相同的角色，参数υ≤1时，冲击影响曲线是凹的，参数υ≥1时，冲击影响曲线是凸的。

在EACD模型的基础上，我们可以得到多种ACD类型，这些模型包括了许多计量学家研究的ACD的不同形式。令λ＝υ＝1，b＝c＝0，便可以得到Engle和Russell（1998）的简单ACD模型（ACD）；令λ→0，b＝c＝0，可以推出Dufour和Engle（2000）的Box-Cox ACD模型（BC-ACD）；令λ→0，υ→0，b＝c＝0，可以得到对数ACD模型类型Ⅰ（L-ACDⅠ），或者λ→0，υ＝1，b＝c＝0，便可以推出Bauwens和Giot（2000）的对数ACD模型类型Ⅱ（L-ACDⅡ）；另外，参照GARCH研究方法，通过对（9-13）式加入限制条件可以构造不同的条件期间模型，这里考虑的例子包括了：λ→0，υ＝1时，得到非对称对数ACD模型（Asymmetric Logarithmic ACD Model，AL-ACD）；λ＝υ时，得到非对称能量ACD模型（Asymmetric Power ACD Model，AP-ACD）；λ＝υ＝1时，得到非对称ACD模型（Asymmetric ACD Model，A-ACD）；λ＝υ，b＝c＝0时，得到能量ACD模型（Power ACD Model，PACD）。Dufour和Engle（2000）在误差项服从指数分布的条件下，提出了一个非对称对数ACD模型，此时b＝1，称之为指数ACD模型（exponential ACD Model，EX-ACD）。表9.11概括了所考虑的所有ACD模型，这里为了方便比较，我们把简单ACD模型及对数线性ACD模型一并列入表中加以分析。

表9.11　ACD模型类型

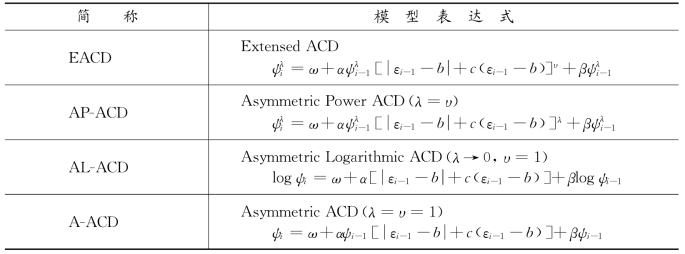
续 表

（二）ACD扩展模型的实证研究

下面用中国石化（600028）2004年2月1日至2004年4月30日期间的实时交易数据估计ACD模型的不同类型。

我们定义中国石化价格期间为价格累计变化0.03元以上的时间间隔；成交量期间为成交量累计变化100万股以上的时间间隔。交易时间每天包括早晨9∶30～11∶30、下午1∶00～3∶00，隔夜以及休市时的时间间隔被剔除。本节先模拟原始时间间隔（即未消除日内效应的时间间隔）的ACD模型，后面我们将考虑消除了日内效应的时间间隔ACD模型，并进行相互比较。

我们用极大似然法来估计表9.11中的ACD扩展模型，假设εi∈i.i.d且具有Burr密度：

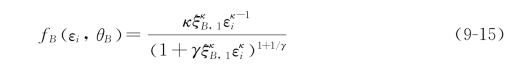
κ＞γ＞0，并且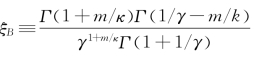表示第m阶动差，m＜k／γ。Burr密度包括Weibull（γ→0）、指数（γ→0且k＝1）和对数逻辑（γ→1）分布。

表9.12和表9.13列出了中国石化价格期间和成交量期间关于ACD各类模型的估计结果。从表9.12和表9.13可以看到，对于任何ACD模型，Burr密度中的参数k和γ的估计值都是显著的，这表明基准风险率函数是非单调的。L-ACDⅡ的对数似然值明显区别于ACD和L-ACDⅠ的值；对比PACD和ACD，可以看出λ值有益于减少对数似然值，说明传统的线性ACD模型强加的约束条件与实际数据相矛盾；对比BC-ACD和L-ACDⅡ，可以看出这里让εi－1的υ次方自由变化对对数似然值的影响不大；对比EX-ACD和AL-ACD，看出当b＜0时，不利于减少对数似然值，对于AL-ACD模型而言，在b＞0和c＜－1的条件下冲击影响曲线是凹的，而凹形冲击影响曲线有利于模型的改善，关于这点我们在后面还会有深入的讨论；对比AP-ACD和A-ACD，尽管AP-ACD里的b是显著异于0的，而A-ACD里b和c参数是显著的，它打破了通常附加的确保期间过程非负性的约束，也就是α＞0、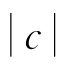＜1，可以看出，当λ≠υ时对数似然值有较为明显的改善（特别是深发展价格期间模型），说明双倍Box-Cox变化（λ≠υ）带来了模型更多的提高。

表9.12　中国石化价格期间原始数据ACD模型实证结果

注：① 价格累积变动至少0.03元。
② 括号内为标准差。
③D-TEST是对数残差的非参数检验概率值（p-values）。

表9.13　中国石化成交量期间原始数据ACD模型实证结果

注：① 成交量累积变动至少100万股。
② 括号内为标准差。
③D-test是对数残差的非参数检验概率值（p-values）。

运用AIC值，表9.13中表现较好的是AL-ACD、PACD、L-ACDⅠ和L-ACDⅡ。

除了原始价格区间以外，我们还考虑了中国石化原始成交量期间的模型模拟。我们可以看到，上述对价格区间的有关分析，对于成交量期间模型模拟同样适用。从表9.13列出的模拟结果，根据AIC值，对于中国石化原始成交量期间而言，表现较好的模型有AL-ACD、BC-ACD以及EX-ACD。

（三）消除日内效应后的ACD各类模型的实证研究

本部分采用与上部分相同的数据，消除日内效应后对ACD各类模型进行了实证，消除日内效应的时间间隔xi＝Di／ρ（ti），Di是以秒计算的原始时间间隔，ρ（ti）表示日内因子，处理方法与前面介绍的方法相同。表9.14和表9.15列出了中国石化价格期间和成交量期间消除日内效应后关于ACD各类模型的估计结果。

从表9.14可以看到，对于任何ACD模型，Burr密度中的参数k和γ的估计值同样都是显著的。与上述不同的是，这里L-ACDⅠ的对数似然值明显区别于ACD和L-ACDⅡ的值；对比PACD和ACD，可以看出λ在（0，1）之间差距很大，λ→1时对数似然值增加明显，λ→0时对数似然值减少明显，说明传统的线性ACD模型强加的约束条件与实际数据相矛盾；对比BC-ACD和L-ACDⅡ，可以看出让的υ次方自由变化导致对数似然值降低很多；对比EX-ACD和AL-ACD，看出由Dufour和Engle（2000）提出的b＝1的AL-ACD模型增加了对数似然值，暗示了非对称性可以发挥作用；对比AP-ACD和A-ACD，尽管AP-ACD里的b是显著异于0的，c的标准差非常大，而A-ACD里b和c参数是显著的，它打破了通常附加的确保期间过程非负性的约束，也就是α＞0、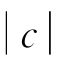＜1。值得注意的是这里EACD模型显示λ＝υ，对数似然值没有明显改善，对比上面的λ≠υ时的对数似然值情况，说明双倍Box-Cox变化（λ≠υ）带来了更多的提高。

与前面原始时间间隔的实证结果对比可以看出，除了原始时间间隔会导致一些模型的ω取值较大外，两者没有其他明显的区别。因此，我们可以对所有模型实证结果一并加以讨论。

运用AIC值，表9.14中表现较好的是EACD、AP-ACD、BC-ACD、EX-ACD和L-ACDⅠ，这些模型与ACD和L-ACDⅡ模型形成了对比，而且，λ自由变化和非对称效应似乎可以相互替代。

表9.14　中国石化价格期间消除日内效应ACD模型实证结果

注：① 价格累计变动至少0.03元。
② 括号内为标准差。
③D-test是对数残差的非参数检验概率值（p-lavues）。

A-ACD和AL-ACD的冲击影响曲线只有在b＞0和c＜－1的条件下是凹的，表9.14中A-ACD和AL-ACD的对应c参数值不满足上述条件，相应的其极大似然值明显偏高。与其不同，如果参数υ小于1，BC-ACD和EACD模型都会产生凹的冲击曲线，在EACD情形下，不管转移和旋转参数如何也同样如此，因此在EACD里不是所有的参数估计值都显著。当PACD模型令λ＝υ时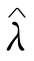的估计值使得BC-ACD和EACD模型中的υ承担了产生凹形冲击影响曲线的作用，对于AP-ACD模型同样如此。初看起来尽管可以通过b和c推导出凹形曲线，然而为了确保一个凹形冲击影响曲线，要求c的绝对值大于1，这样就违反了期间过程非负性的约束，事实上，PACD模型通过模仿AL-ACD模型让λ趋于0来避免这个问题。

过去对于模型设定的检验一般仅执行简单的诊断测试以检验残差是否是独立同分布的，所有的论文都使用Ljung-Box统计以测试序列相关性，然而只有少数测试了误差项的分布是否被正确设定。至于国内文献则显得更为简单，一般仅通过对比模型拟合值与实际值的比较图，进行并不客观的判断。至于不同类型ACD模型的对比则只能依靠极大似然函数值的大小来判断，我们可以从上述实证中发现，对于极大似然函数值或者AIC值的判断，由于大多数模型在极大似然函数值和AIC值上的差距并不大，依靠这些值来判断，则显得有些困难，或者是有可能得出错误的结论。因此，对于模型设定的检验需要探索更加有效的方法，这一点我们将在下一部分探讨，对于本部分列出的D-检验值的分析一并加以详细阐述。

除了价格区间以外，在此还考虑了中国石化成交量期间消除日内效应后的模型模拟。我们可以看到，上述对价格区间的有关分析，对于成交量期间模型模拟同样适用，在此就不再赘述。从表9.15列出的模拟结果，根据AIC值，对于中国石化成交量期间而言，表现较好的模型有EACD、AP-ACD、AL-ACD以及BC-ACD。