资产组合投资的风险与收益曲线

一、关于模型的基本假定

马科维茨模型从理论上解决了投资者的最优投资决策问题,但这种模型是以数学、统计学为基础的,繁复的计算使该理论缺乏可操作性。为此,斯坦福大学教授威廉·F.夏普在1963年提出了证券组合选择的新方法,即资产资本定价模型(CAPM)。

资本资产定价模型有以下的基本假设:①投资者是厌恶风险的,其目的是使预期收益达到最大;②所有的投资者对所有证券的均值、方差都有相同的估计;③不考虑税收因素的影响;④完全的资本市场,即无交易成本、所有资产完全可分、投资者是价格制定者、所有资产数目一定;⑤存在无风险资产,投资者可在无风险利率下进行无限制的借贷;⑥资本市场处于均衡状态。

二、市场组合与资本市场线

(一)分离定理

在分析资产的有效组合时,可以发现:当一种风险资产与无风险资产进行组合时,投资者都会选择同一个风险资产;当用多种风险资产与无风险资产进行组合时,所有投资者都会选择相同的风险资产组合,然后将它与无风险资产进一步进行组合。于是,投资者的整个最优选择过程可以总结为两个步骤:寻找合适的风险资产组合,这时不必考虑投资者效用的无差异曲线;确定风险资产与无风险资产的投资比例,这时必须结合投资者的无差异曲线。

这是托宾(Tobin)提出的著名的“分离定理”。所谓分离定理是指投资者在进行风险资产与无风险资产组合的选择时,可以按上述两个步骤进行,这就意味着投资者的收益与风险偏好与其风险资产组合的最优构成无关。托宾的分离定理是建立在马科维茨的全协方差模型的基础之上,它要求计算组合内的每一种资产的均值、方差及资产间的关系,计算量很大。

后来,夏普对此模型进行了修改,他针对全协方差模型在计算方面的缺陷开发了新的指数模型——资本资产定价模型,使计算量大大简化。马科维茨的资产组合选择理论可以看作是投资者行为理论,即考察单个投资者在追求效用最大化情况下的行为模式;而夏普的资本资产定价理论是一个市场均衡定价模型,他确切地描述了市场均衡状态下投资者期望收益是如何决定的。

(二)市场组合

根据分离定理,在均衡状态下,每个投资者都拥有相同的风险资产组合D,并且该组合中每种证券的构成比例都等于该证券市场价值在全部证券的市场价值中的比例。这是因为,如果某种证券在组合中的比例小于其市场价值占全部证券市值的比例,说明其需求量小于供给量,该证券的价格就会下降,使其预期收益上升,从而会吸引投资者购买,使得其需求量上升。相反,如果对某种证券的需求量超过其供给量,也即在组合中所占的比重超过其市值在全部证券市值中的比重,则该证券的价格将会上升,导致其预期收益下降,使得其需求量减少,最终使得供需平衡。

因此,市场组合就是所有投资者都按同一比例持有的组合资产,记为M。从理论上说,市场组合不仅仅包含普通股,还包括优先股、债券、不动产等所有风险资产,但由于上述资产在实践中的难以观测,即真正意义上的市场组合是难以确定的,这种情况下,可以用普通股形成的组合来替代。

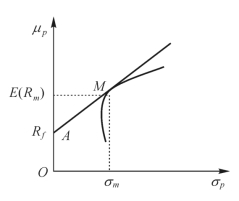
图8-4　资本市场线

(三)资本市场线

当市场存在着无风险的借贷利率Rf时,在图形上作一条直线连接Rf与M,从而形成允许无风险借贷情况下的线性有效集合,我们称该集合的线性表示为资本市场线,如图8-4所示,资本市场线上的每一个点(即每一个组合)都优于不经过市场组合的组合以及不采用无风险借贷时的组合,因为其他组合都位于资本市场线的下方。

若要求解资本市场线上任一组合的收益与风险,只要写出资本市场线的方程即可。设该线上任一点的收益为Rp,方差为σp,则根据两点决定一条直线的原理,资本市场线的表达式为:

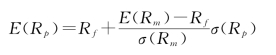
从这个式子可以看到,资本市场线所表示的是组合的收益与其风险之间的一种线性关系,其斜率表示单位风险的收益。应该注意的是,这里的组合指的是有效组合,也即资本市场线表示的是有效组合的收益与风险之间的线性关系。

(四)证券市场线

在无效性的投资组合与其他个别证券的风险与收益条件下,资本市场线很难对其收益与风险进行衡量。为此,须用证券市场线的模型来进行描述,即:在市场均衡状态下,证券的期望收益率与系统性风险的关系可表示为:

公式中E(Ri)表示第i个风险资产的期望收益,E(Rm)为组合资产的期望收益,σim为第i种资产与组合M收益之间的协方差。该公式表明,在市场均衡状态下,风险证券或组合的期望收益率,是它与市场组合收益的协方差的线性函数。

(五)资本资产定价模型

在证券市场线数学模型中,证券的系统性风险是用协方差来表述的,但人们习惯于以市场组合作为衡量风险的标准,即用证券或组合的协方差相对于市场组合方差的倍数来说明证券或组合相对于市场组合的风险。若令:,其中βi表示i相对于市场组合的风险,称为β系数,则证券市场线可以简化为:

E(Ri)=Rf+βi[E(Rm)-Rf]

上式是引入了β系数后的证券市场线表达式,同时也是资本资产定价模型的数学表达式。在资本资产定价模型中风险衡量单位βi,我们称其为市场风险。当投资者将其财富分散投资在许多资产时,个别资产的风险会变得越来越不重要,而投资人所面临的总风险会变成资产彼此间的协方差。βi衡量个别资产和市场之共变情形,并以市场组合收益率的标准差σ进行标准化,在此设定下,市场组合之市场风险βm等于1。

三、套利定价理论

资本资产定价模型建立在对投资者偏好的一系列假设的基础上,而这些假定常与现实不符,在检验资本资产定价模型时,难以得到真正的市场组合,甚至有一些经验结果完全与之相悖。为了探讨更具有广泛意义和实用性的投资组合理论,1974年罗斯提出了一种新的资本资产均衡模型——套利定价模型(APT)。

(一)模型的基本假设

套利定价的模型,不需要像资本资产定价模型那样对投资者的偏好作出很强的假设,只要求投资者对于高水平财富的偏好,胜于低水平财富的偏好,对风险资产组合的选择也仅依据收益率。即使该收益与风险有关,风险也只是影响资产组合收益率众多因素中的一个因素,因此,罗斯的套利定价模型的假设条件,要比夏普的资本资产定价模型更为宽松,因而更接近现实、更具有实用价值。罗斯的套利定价模型认为,因素模型是决定证券价格的基础,而套利行为则是使证券价格达到均衡的推动力。

套利定价理论有以下的基本假设:(1)资本市场是完全竞争、无摩擦和无限可分的;(2)所有投资者对同种资产的收益具有相同的预期;(3)在资本市场上,存在着充分多的资产;(4)资本市场中不存在着任何无风险的套利机会;(5)投资者都相信证券i的收益受到k个共同因素的影响。

(二)套利机会与套利定价

套利是指利用同一资产在不同市场或不同资产在同一市场上存在的价格差异,采用低买高卖的策略而获利的现象。如同一资产在两个市场上的定价不同,投资者就可以在价格较高的市场上卖空该资产,同时用所得资金在价格较低的市场上买入该资产,这时他就可以获得一个确定的正的价差。又如,风险相同的两种不同资产在同一市场上的收益不同,投资者也可以卖空收益较低的资产,同时买进收益较高的资产而获得确定的正收益。

在上述两种情形中,有两点值得特别注意:(1)上述操作所获得的投资收益是确定的,也即是无风险的;(2)投资者的投资金额为零。这就是说,如果市场上存在着套利机会的话,投资者可以用零投资获得确定的正收益。在这里可以将套利机会定义为,由于市场上对资产定价的差异,而导致的可通过低买高卖策略而以零投资获得无风险的正收益的可能性。

套利机会一旦被投资者发现,就会被加以利用进行套利,这一行为会使得价格差异很快消除。套利者不断卖空定价较高的资产的结果,会使其供给上升,从而导致价格下降。相反,套利者不断买空定价较低的资产的结果将使其需求上升,从而使得其价格也上升。显然,这样的套利机会在市场上不可能长期存在,随着套利活动的增加,套利的机会将不复存在,所有资产都将被正确地定价,也即同类资产在同一市场应该具有同样的价格水平,这就是价格同一律的原理,当市场达到有效并处于完全竞争时,在市场均衡的条件下,由于价格同一律的原理,市场中将不存在套利的机会。

APT与CAPM两者都是利弊兼而有之,但却同样说明了风险与收益间的关系是符合理性的——更多的系统性风险,更高的预期收益。