【摘要】:在晶体中,两种对称要素的组合可导出第三种对称要素,它的作用为前两种对称要素作用之和,这被称为对称要素组合定理。写成公式为:依据该公式可推出对称要素组合有:定理2:如果有一个P平行包含Ln,则必有n个P同时包含平行Ln,且相邻的两个P的交角为Ln的基转角的一半。
对称要素组合定理_结晶矿物学
四、对称要素组合定理
在自然界,所有晶体均具有对称性。一种晶体中可以出现有一种对称要素,也可以出现有多种对称要素的组合。在晶体中,两种对称要素的组合可导出第三种对称要素,它的作用为前两种对称要素作用之和,这被称为对称要素组合定理。晶体中出现的对称要素组合定理表征如下:
定理1:如果有一个L2垂直Ln,则必有n个L2同时垂直Ln,且相邻的两个L2的交角为Ln的基转角的一半。写成公式为:
![]()
依据该公式可推出对称要素组合有:
![]()
定理2:如果有一个P平行包含Ln,则必有n个P同时包含平行Ln,且相邻的两个P的交角为Ln的基转角的一半。写成公式为:
Ln×P∥→LnnP
依据该公式可推出对称要素组合有:
L2×P∥→L22P;L3×P∥→L33P;L4×P∥→L44P;L6×P∥→L66P。
定理3:如果有一个P垂直Ln,n为偶数时,则在其交点必然存在C。写成公式为:
Ln×P⊥→LnPC
依据该公式可推出对称要素组合有:L2×P⊥→L2PC;L4×P⊥→L4PC;L6×P⊥→L6PC。
![]()
依据该公式可推出对称要素组合有: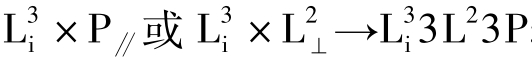 ;
;
![]()
定理5:如果一个Lm与Ln斜交,夹角不等于0°、90°、180°,则在Lm周围均匀分布有m个Ln,则在Ln周围均匀分布有n个Lm。写成公式为:
Lm×Ln→mLnnLm
对称要素的这五个组合定理已经过数学严格的证明,在晶体对称要素应用中具有重要的意义。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















