矿产资源靶区定量预测方法

3．3　矿产资源靶区定量预测方法

矿产资源靶区定量预测模型的建立，是在综合信息找矿模型的建立、各级地质统计单元划分、相应各级统计变量研究的基础上，应用各种有关的统计数学方法。最常见的数学方法是特征分析和逻辑信息等。

3．3．1　特征分析

特征分析是一种多元统计分析方法，它通过对控制区内已知样品的研究，查明变量之间的内在联系并确定它们的找矿意义，从而建立起特定类型矿床的定量模式。预测时将预测对象的地质特征与模型对比，用它们的相似程度表示预测对象的成矿可能性，据此圈定出有利成矿的各级远景区。

特征分析原理简单，易于掌握。在应用中可根据需要灵活运用解决不同问题，便于发挥地质人员的经验和知识，因而受到重视。它在矿产资源评价中常常用来解决资源量的定位问题。由于使用的计算方法不同，特征分析有不同的模型。目前使用的三种模型是：乘积矩阵法、矢量长度法、乘积矩阵主分量法。

1．变量的定义、赋值和样品的选取

（l）变量的定义和赋值

特征分析用于矿产资源总量预测，主要是解决地质环境的对比。对研究对象的成矿有利程度进行分辨，即区分矿的“有”、“无”问题。因此对变量的考虑应该从它们对成矿和找矿的有利、不利角度出发。从这个意义上来突出变量对矿的指示作用，使模型的含义更加明确。因此在定义变量时，应以定性分析为前提，提出地质依据，给出合理的赋值规则。

特征分析使用的是离散数据，它把从各种原始资料中获取的与成矿找矿有关的信息，转化为二态（1，0）或三态（1，0，－1）取值的变量。对连续取值的实测变量以及合成变量，需要按上述考虑进行离散化处理。例如，某指示元素含量值是一个连续量，由经验知道含量越高越有利于成矿，于是可根据实际情况给出一个临界值α，凡含量值大于α就赋给1，否则赋给0。这是对简单情形的赋值规则。如果研究的是物探变量，这样做显然是不够的，因为由实测值高低来赋值没有考虑地球物理背景场的作用，因而难以表现矿和非矿的特征。若改用局部异常的有无或异常某种特征的是非来赋1和0，那么这个变量就可能反映出矿和非矿的区别，成为有意义的变量。

由此可见，变量的转换赋值应经过详细研究并作一定的数学处理来完成。还应说明，不同地质环境中的同一个变量，它的赋值标准可以不同。比如磁异常，甲区强异常指示矿化，乙区弱异常指示矿化，这就需要用两个不同的标准来定义1，这样做尽管两者所用的标准不同，但1的含义是一致的。当然，在预测时也可按此考虑。

对于变量未查明或作用不清的情况，二态和三态赋值都用0表示。经过赋值以后，有些变量的作用就比较清楚了。例如，在全部矿床上都取0的变量显然没有意义，应予以剔除。在使用第三种模型概率矩阵主分量法时，取值全1的变量也是没有意义的。经过整理，假定剩下m个变量，将它们排成一个数表，形成所谓变量矩阵。

（2）单元的选取

特征分析使用的单元，可以是网格单元，也可以是地质体，一般后者的应用不如前者广泛，因为它需要有较高的工作程度和资料水平。模型单元和预测单元应有一致的定义，用网格单元建立的模型只能应用在同样大小的预测单元上，而地质体模型只能在同类地质体上预测。建立模型所用的单元，可以在研究区内选出，也可由研究区外地质条件相似的地区选出。不论使用哪种方法，其前提条件是必须保证模型与预测对象具有可类比性。

特征分析的实质是通过对有矿单元变量之间相互关系的研究，综合矿床的共同规律，或者说典型特征。这个规律或特征应当是矿化的表现，因此要选用有矿单元建立模型，而且有足够的数量以保证模型的代表性。

对于一个工作程度较低、已知矿床很少的地区，使用一些与已知矿床地质条件相似的未知单元与矿床一起建立模型，也是可行的方法。这时，建立的模型实际是矿床模型的推广。

2．变量的权系数

所谓变量的权，是用某种方法对变量重要性进行度量给出的数量指标。由于它经常以乘积因子的形式与变量发生关系，所以也称权系数。

假设对m个变量在n个单元上进行赋值，得到矩阵XnXm，现在我们从X出发，计算各个变量的权。

（1）用乘积矩阵矢量长度法求变量权

下面在二态赋值的假定条件下来讨论。

前面已述，矩阵XnXm的每一列都是一个变量，那么乘积x′x＝R中的元素r_ij是第i个变量与第j个变量对应元素乘积之和：

可见R是表现变量之间关联的矩阵。实际上r_ij还可以用这样的办法来计算：在矩阵X中，查出第i列和第j列中取值同时为1的次数就是r_ij。如果把两变量在一个单元上同时出现（取值为1）叫作一次匹配的话，那么r_ij显然就是第i个变量和第j个变量的总匹配数。

可以看出，矩阵R的第一行r₁₁，r₁₂，…，r₁ m是第1个变量与所有变量的匹配数，一般地，R的第i行是第i个变量与所有变量的匹配数。在R中如果某一行的数都较大，说明这个变量与其他变量的关系要密切些。由变量和单元的选取原则可以看出，与其变量越密切，变量在说明矿床模型的总体特征上作用也就越大，因此可以用来衡量变量的重要性。由于r_ij的值不为负，所以R的行平方和具有与行和同样的度量性质。从向量的角度看，矩阵行平方和有明确的几何意义，它是行向量长度的平方，因此用它来表现变量的重要性，定义为第i个变量的权系数：

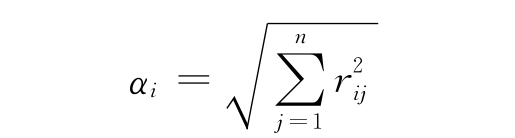
例如，有5个样品中4个变量做成的矩阵：

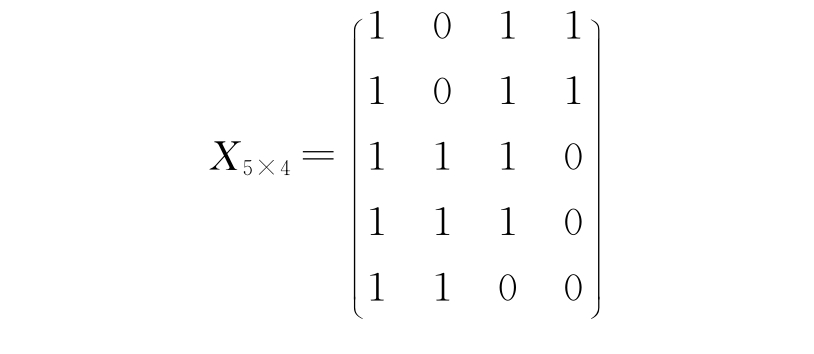
算得：

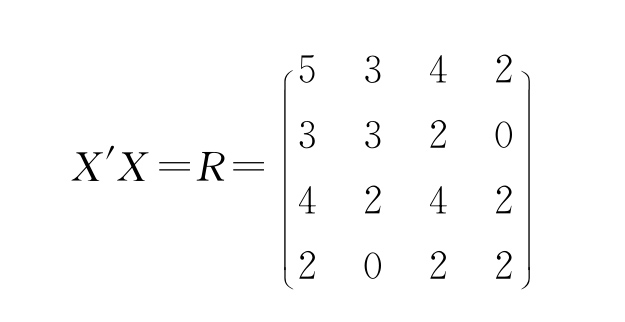
于是变量的权为：

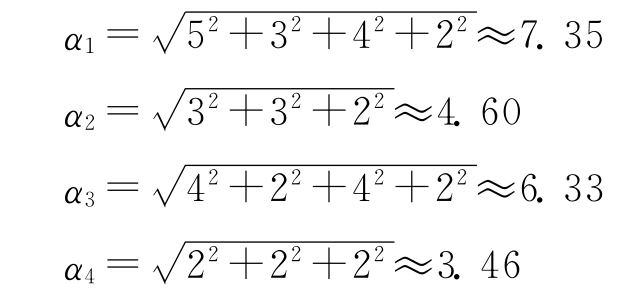
（2）用乘积矩阵主分量法求变量权

使用前面讨论的乘积矩阵X′X＝R，我们来求它的特征值和特征向量。设λ是R的特征值，ξ^→是对应于λ的特征向量。它已经标准化，于是：

两边同乘ξ^→′

将X按行（单元）表示为向量形式，有：

Xξ→的各个分量a_iξ→是第i个单元在特征向量ξ→上的投影长，因而数量积（Xξ→）′（Xξ→）＝λ是各单元在特征向量ξ→上的投影平方和。如果把单元看作是变量空间中的点，那么单元点群的长轴方向就可以看作是典型特征。这个方向，就是最大特征值λ_i所对应的特征向量ξ→i的方向。在这个方向上，单元点投影平方和最大，或者说，单元点有最大的离散程度。这个特征向量的各个分量，即它在各原变量上的坐标，表现了变量与特征向量之间的密切程度，或者说它反映了变量在造成这个特征方向上所起的作用。因此，我们用最大特征值λ_i所对应的特征向量ξ→i的各个分量来作为各变量的权系数。

求矩阵X′X＝R的特征值和特征向量通常都在计算机上完成，有些计算机还备有专门的计算程序供使用。

例如，在

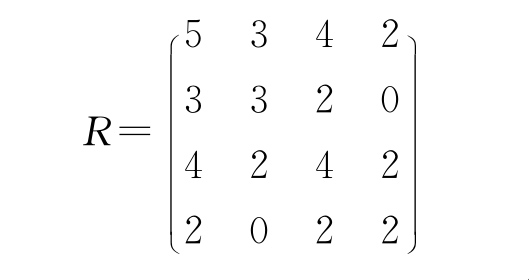
算得最大特征值λ_i＝11．01，相应的特征向量ξi＝（1．000，0．586，0．856，0．412），于是就有α₁＝1．000，α₂＝0．586，α₃＝0．856，α₄＝0．412作为各变量的权。

（3）用概率矩阵主分量法求变量权

下面假定变量为三态取值。

变量的匹配表示了两两变量之间的关联，匹配数的大小，反映了变量有相同取值情况的多少。现在继续研究变量之间这种匹配的意义，为此对匹配的概念作如下解释：两变量在一个单元上同时取1称正匹配，同时取－1为负匹配，其他取值则为不匹配。这样，两变量的匹配数就定义为变量在各单元上正匹配和负匹配之和。有了匹配数的概念，就可以定义匹配概率了。设两变量X_i和Xj的实际匹配数为K，将变量的取值任意排列重新计算匹配数，在所有的排列当中使匹配数η小于K的排法所占的比例就称作两变量的匹配概率，记为P_ij。

匹配概率可看作是对变量现有匹配好坏的衡量。由于重排变量使匹配数η发生变化，若η在所有的排法中都比K小，说明变量匹配数K达到最高，换任何一种排法都不如现在的匹配。因此，η＜K的机会大小反映了变量现有匹配关系的好坏。由此可见，匹配概率不是从匹配数的大小而是从匹配的意义来表现变量的关联性。

例如有两个变量X1和X2，其中：

X1＝（1 1 0 －1）

X2＝（1 1 －1 0）

它们的实际匹配数K＝2，把变量X2重新排列，共有12种排法。表3-1列出了Xa的全部排列及其与X1的匹配数。

表3-1　变量X₁、X₂匹配表

在12种排法中，匹配数η小于2的排法有8种，因此X1和X₂的匹配概率为

再如变量X3，X4

X3＝（1 －10 0）

X4＝（1 －10 0）

现在匹配数K也是2，把X4重排，如表3-2所示。

表3-2　变量X₃、X₄匹配表

算得匹配概率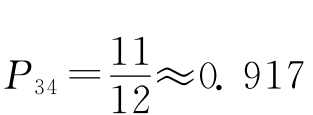

上面是仅对两变量中的一个变量重排算得的概率，可以证明，它与两个变量都重排结果相同。由这两个例子可以看出用匹配数和用匹配概率对变量的度量结果有差异。X1，X2的匹配数和X2，X4相同，但匹配概率却不同，P24较P12大。从实际意义来看，X2和X4是同一变量，按理一个变量与自身的关系密切是理所当然的。

根据定义容易得出，变量匹配概率具有对称性，因此由两个变量匹配概率形成的矩阵P是一个对称矩阵。其中对角线元素是变量自身匹配概率，仿照乘积矩阵主分量方法，对P求最大特征值，用相应的特征向量的分量作为各变量的权系数。

匹配概率和匹配数一样也是对变量之间关联程度的衡量，匹配概率从另一个角度表现了变量的依存关系。和其他方法一样，它也受一定条件的限制。例如，对于取值为1的变量，虽然它在所有矿床上都表现为有利，但它与其他变量的匹配总是0，因而在这种度量意义下不能提供任何信息而被剔除。

3．计算单位的关联度（模型的使用）

设已用某种算法求得了变量的权α₁，α₂，…，α_m，这些权值的符号和大小反映了变量的重要性。将变量权按绝对值大小排队，就可以区分变量的找矿意义。其中权值为0或接近0的变量，在进一步研究中被去掉。用剩下的1个变量建立起关系式：

此关系式是矿床的定量模型。其中X_ij是第i个样品在第j个变量上的取值。α_j是变量的权，Y_i称为关联度或联系度，它是第i个单元在1个变量上的得分。由模型的建立可以看出，关联度Y值是反映矿化信息的一个综合指标。因此，我们能够通过对模型单元关联度的研究，得出有利成矿的数值范围，形成找矿标准，也能通过对预测单元关联度的研究，估算矿化的可能情况，确定有利成矿的远景地段。

例如，在前面的例子中，有5个单元，每个单元的关联度为：

Y1＝7．358×1＋4．69×0＋6．33×1＋3．46×1＝17．14

Y2＝Y1＝17．14

Y3＝7．35×1＋4．67×1＋6．33×1＋3．46×0＝18．37

Y4＝Y3＝18．37

Y5＝7．35×1＋4．69×1＋6．33×0＋3．46×0＝12．04

可见单元Y3＝Y4＞Y1＝Y2＞Y5

各种各样的使用关联度圈定成矿远景区的方法，都基于同样一种认识，关联度是表现预测对象与模型总体特征接近程度的量。Y值越大，说明变量在单元上表现有利情况越多，因而就越有利于成矿。例如，以网格单元为研究对象，将每个预测单元算出关联度，那么与模型最接近的那些单元集中区就可认为是有利成矿的地区。当然所谓接近只是比较而言，有些情况下预测单元的关联度可以达到模型单元关联度的水平，而在另外情况下预测单元可能与模型相差较大，因此要具体研究。一般造成矿预测区关联度普遍偏低的原因有两条：一是预测区成矿条件差，二是预测区工作程度不够。这两条都可形成系统误差，但意义却不同，需要加以分辨。

4．矿床模型的推广

这里来讨论广义的矿床模型，假定以网格单元为研究对象。所谓广义矿床模型，是指模型单元不限于已知的有矿单元，还可扩充一定数目的与有矿单元关联性强的未知单元。显然建立这样的模型是有意义的，因为在某一地区研究某类矿床，常常会遇到已知矿床少的情况，尽管可以从其他地区借用一些同类矿床建立模型，但是由于地质环境的差异而使模型仍受很大限制。再者即使有足够的已知矿床来建立模型，也存在地质变量本身的区域性变异，时常造成预测区与模型区较大差异而难以类比的情况，适当选取未知单元加入模型，可在一定程度上克服上述困难。

下面研究建立广义矿床模型的方法。设已知有矿单元s个，原始变量m个，这些变量用三态赋值形成数据矩阵XsXm。

第一步，从矩阵XsXm出发，用乘积矩阵主分量法给m个变量赋权，剔除权值接近于0的变量，用剩下u个重要变量来计算未知区单元关联度Y。从未知区找出关联度高的前l个单元，来研究这些单元与s个有矿单元之间是否有较密切的关联性。

第二步，为研究未知单元与有矿单元的关联性，先计算u个变量之间的匹配概率。这u个变量在原来的s个有矿单元中有较多的匹配，因而获得了较大的权值。现在的问题是：在加入1个未知单元以后，这u个变量的关联性有无变化，变量之间的匹配数虽然也是对变量关联性的度量，但它受±1的个数影响很大。在加入未知样品以后，使用匹配概率来表现变量关联性可能更好些，因为影响匹配概率大小的主要因素是变量的构形而不是±1的个数。

使用匹配概率矩阵主分量方法求得u个变量的权，权值小的变量，说明它在后选入的l个样品中与其他变量构形不相似，故使关联性减弱。

第三步，变量权值的变化对样品得分有什么影响？为研究这个问题，用新的变量权重新计算l个未样品的关联度。这些单元已经过一次挑选，如果某单元的新关联度仍然很大，说明它在原来s个变量下具有较大的关联性不是偶然的。因此，再一次根据关联选取样品，得到P个单元，把它们与已知有矿的s个单元合在一起共有n个。

第四步，建立预测模型。u个变量经第二步工作被剔除一些，剩下的v个变量在原模型和新模型中都表现了较密切的关联性。这v个变量在n个单元上的取值，构成新的数据矩阵ZnXv，再使用乘积矩阵主分量方法求v个变量的权，建立关系式：

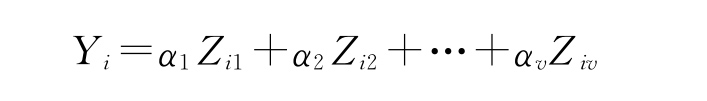
这就是广义的矿床预测模型。

广义模型的建立，是一个扩充单元的过程，它的目的是找出与已知矿床有关联的未知单元来加入模型；同时它又是一个缩减变量的过程，它的作用是尽量消除由变量空间变化造成的系统差异。由此可见，这一过程还可以反复进行。事实上，如果将关联度规格化处理，使Y在（－1，1）上取值，那么过程重复到一定次数之后，Y值就趋予稳定，不再有大的变化了。