第四节 简式拖曳式流变仪的研制
一般来说，测定材料的流变性质是在一定条件下，对试料施加切应力（或剪切变形），跟踪受力后的应变响应（或应力响应）对时间的函数关系，得到流变参数。所施加的应力在理论上简单解析，在实验上能够实现，本节的拖曳式简式流变仪，按照这个思想设计。该流变仪受落球法思想启发，因此有必要先介绍落球法思想。
物体在流场中受到的与流动方向相反的流体作用力称为绕流阻力。牛顿于1726年提出了绕流阻力的计算公式（据鲁钟琪和郑洽余，1980；李玉柱和苑明顺，1998；章梓雄和董曾南，1998）：
式中：ρ为流体密度；U∞为流体受扰动前相对于绕流物体的流速；A为绕流物体在垂直流向方向上的投影面积；CD为绕流阻力系数，主要取决于绕流物体的形状与流动雷诺数Re：
式中：d为投影面A的特征长度；μ为流体的动力黏度；Re也受物体表面的粗糙度、来流的紊流强度等影响。
对于雷诺数较小（Re《1）的圆球绕流，斯托克斯通过对N-S方程的简化与分离求解，得到层流流动的绕流阻力系数：
将式（4-21）、（4-22）代入式（4-20）得到：
式中：η为层流的黏度。
这就是斯托克斯绕流阻力公式。落球法黏度计基于上述原理研制。在实验中，半径为r、质量为m的光滑小球先作加速运动，随着速度的增大，绕流阻力也增大，最后小球达到平衡状态，做速度为v的垂直向下匀速运动（图4-7），小球在绕流阻力D、重力G、浮力F下平衡。
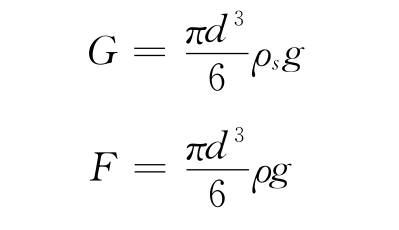
圆球的受力平衡方程为：
G＝D＋F
可解得：
式中：V为小球体积。
斯托克斯公式的适用条件是小球在无限宽广、均匀的流体中下落；而实验时，流体总要盛放在一定的容器中，其边界不可能是无限宽广的，即小球不可避免会受到容器壁及流体有限深度的影响。兰登堡从实验中总结出小球在圆筒形容器的流体中下落时受到的绕流阻力的经验公式：
式中：R和H分别为圆筒的内半径及容器中流体的深度。一般实验中，H》r，因此，流体有限深度的修正项3.3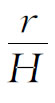
可以不考虑。此为落球法黏度计（图4-7）的工作原理。
但是，落球法黏度计只能测定透明低黏度材料的参数，而在物理模拟实验中所使用的材料一般都不是透明的，黏度相对也较大。为此，我们对落球法流变仪作了如下改进（图4-8）：通过增加拖曳装置的拖曳力，使小球能在较高黏度材料中运动；通过拽绳记录位移/速度装置，使其能测定不透明材料的相关性质。
拖曳式流变仪工作时，小球在拖曳装置的作用下，向下运动，并达到平衡。对于中、高黏度的流体，选用适当半径的轻质小球，可以满足Re＝2ρvr/η《1。半径为r的小球在黏性流体里匀速下落时受到的绕流阻力为：
由于材料的黏滞性较强，小球在材料中所受到的浮力可以忽略。忽略小球运动过程中的升力等，在拖曳装置的作用下，小球在黏性流体中做变加速运动，并达到平衡，满足如下条件：
f＝（m1＋m2）g
式中：m1为小球的质量；m2为拖曳系统的质量。
小球运动过程中，材料所受剪应力可以近似地表示为：
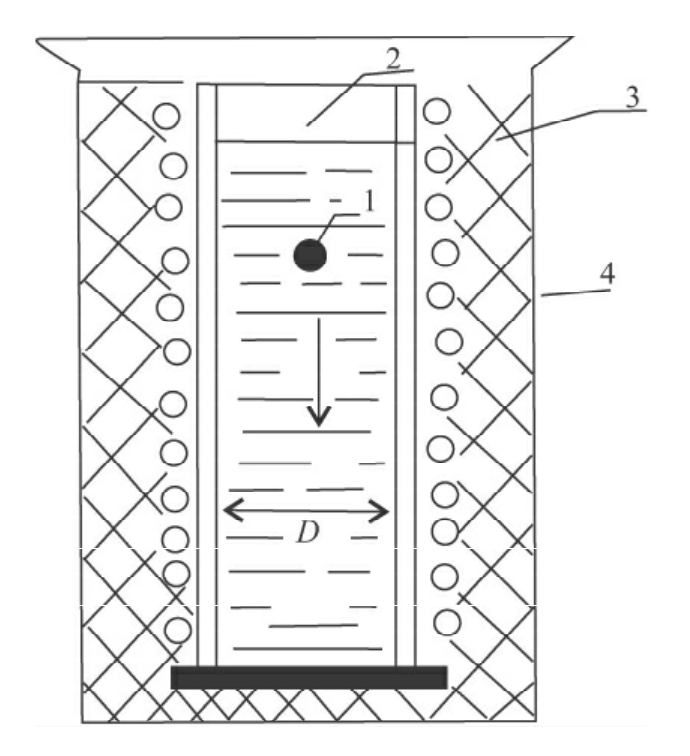
图4-7 落球法黏度计的结构简图（周彦豪，1988）
1.小球；2.黏度管；3.加热器；4.外套
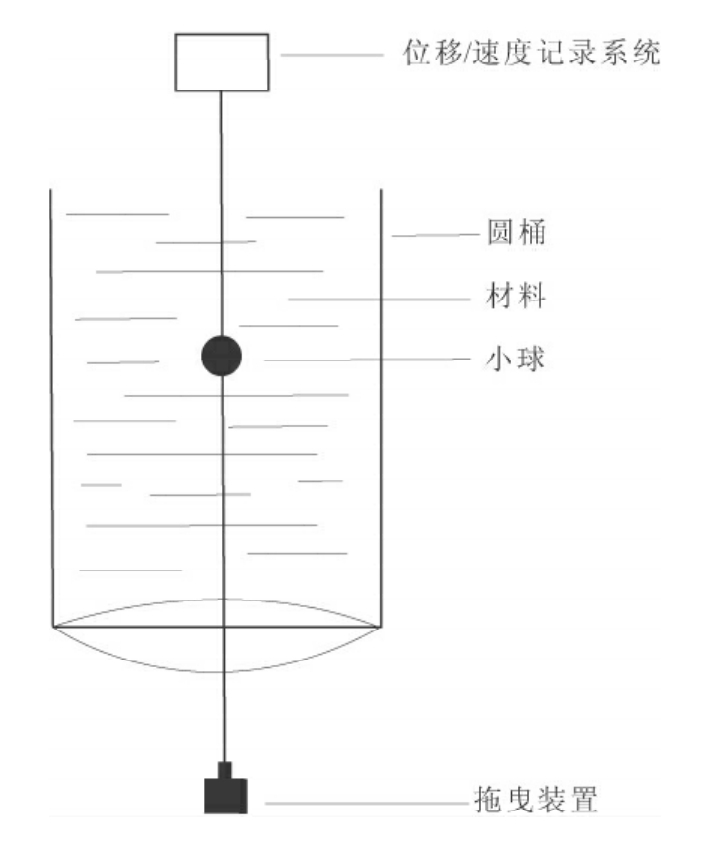
图4-8 拖曳式流变仪结构示意图
材料的剪应变速率（赵得禄等，1981）可表示为：
当剪应变速率在一定范围内时，材料的流变性质满足幂律方程：
式中：n为应力指数；K为流度。
求出小球运动过程中材料的τ和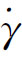
，通过作lg6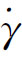-lgτ图，即可求出材料的应力指数n。
我们曾经设计过一台简式拖曳流变仪，由如下几部分组成：电源、打点计时器、支架、料筒、小球、钢丝、重物。电源给打点计时器供电，共同组成本流变仪的位移/速度计录装置（图4-9）。
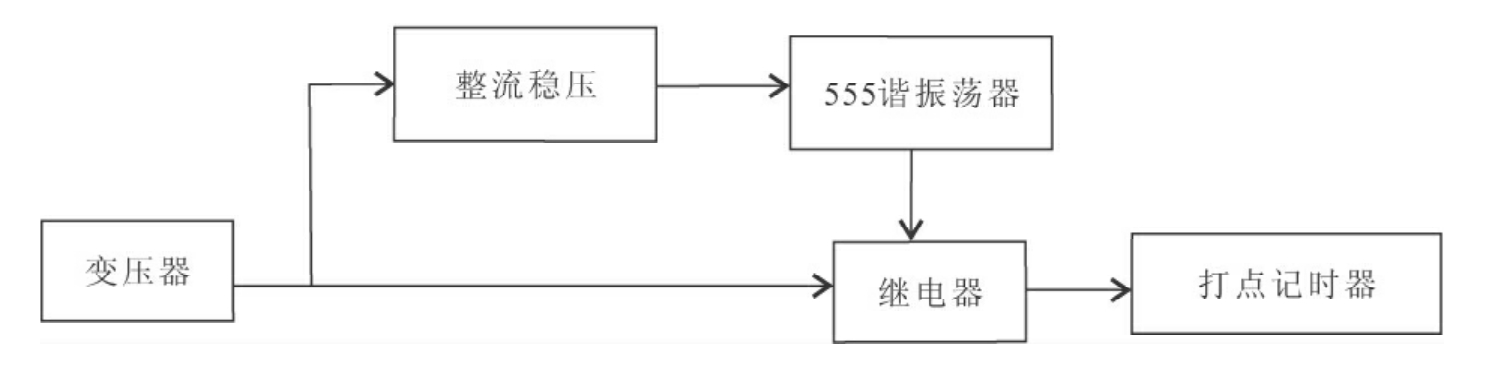
图4-9 简式拖曳式流变仪电源功能模块
这个装置选配了两个轻质塑料小球，其半径分别为2.82mm、3.74mm，质量分别为0.095 5g、0.226g；料筒的内半径为40mm，深105mm。
根据打点计时器的工作要求，本装置的电源为一低频、低压、低功率的正弦波电源。工作参数为9V，1Hz。
本装置所使用的打点计时器为J0203型电磁打点计时器（图4-10）。纸带上相邻两点间的时间间隔为T。
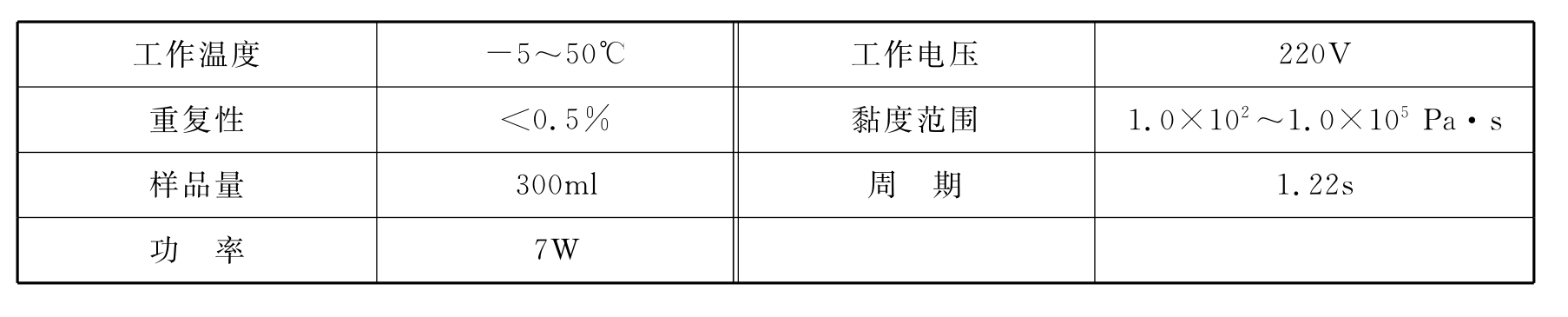
我们对流变仪的主要物理参数做了较严格的标定。主要的测试工作有：配备小球2个，游标卡尺（精度0.02mm）测得球半径分别为2.82mm、3.80mm，FA/JA系列上皿电子天平测得球质量分别为0.096g、0.223g；加工料筒2个，游标卡尺（精度为0.02mm）测得筒内径、深度分别为32.96mm、90mm及40.48mm、104.5mm；另外，本流变仪的主要技术指标如表4-5。
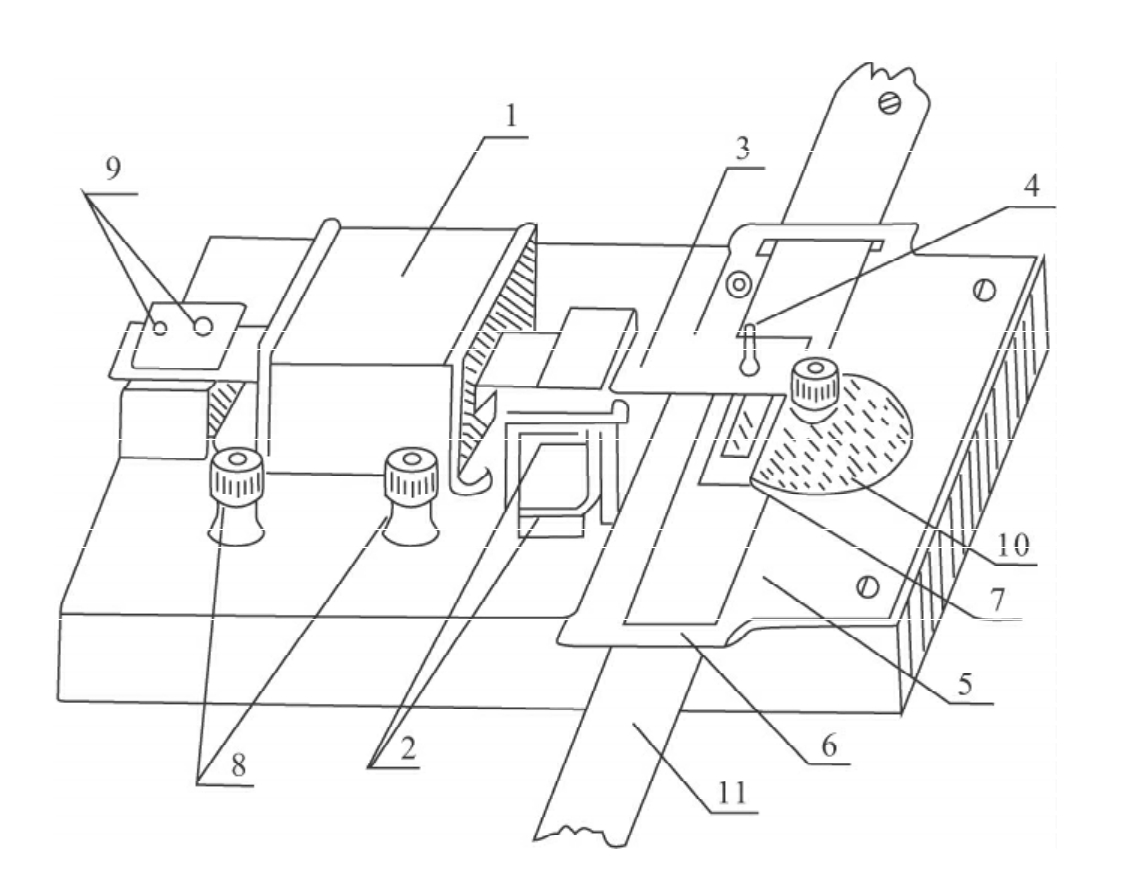
图4-10 打点计时器结构图
1.螺线管；2.永久磁铁；3.振动片；4.打点针；5.基板；6.纸带限位孔；7.压纸框架；8.接线柱；9.螺钉；10.复写纸；11.纸带
表4-5 简式拖曳流变仪主要技术指标
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
