四个分部类的棋盘式平衡模型

第一节　四个分部类的棋盘式平衡模型

一、四个分部类的棋盘式平衡模型

棋盘式平衡表的纵横平衡就像数学中的幻方、游戏中的魔方，纵横牵制，牵一发而动全身。要用凑数的方法去搞平衡肯定是力不从心。计划经济时期的平衡部门就像救火队，这里刚搞平，那里又不平了，整天疲于应付。平衡有没有规律可循？

模仿投入产出模型，我建立了新的棋盘式平衡模型。虽然是模仿，但两种模型的意义完全不同。

投入产出模型是AX+Y=X，其含义是中间产品+最终产品=总产品，由此式推导出Y=（I-A）X，再推导出X=（I-A）^-1Y，为了表彰列昂惕夫所作的贡献，（I-A）^-1被称为列昂惕夫逆阵。

新的棋盘式平衡模型是AX=X，其含义是总收入=总支出，即货币回流，由此式推导出（I-A）X=0，即总收入-总支出=0。为了表彰我做的贡献，（I-A）能否称作杨斌林方阵呢？

表5-1　四个分部类的棋盘式平衡模型

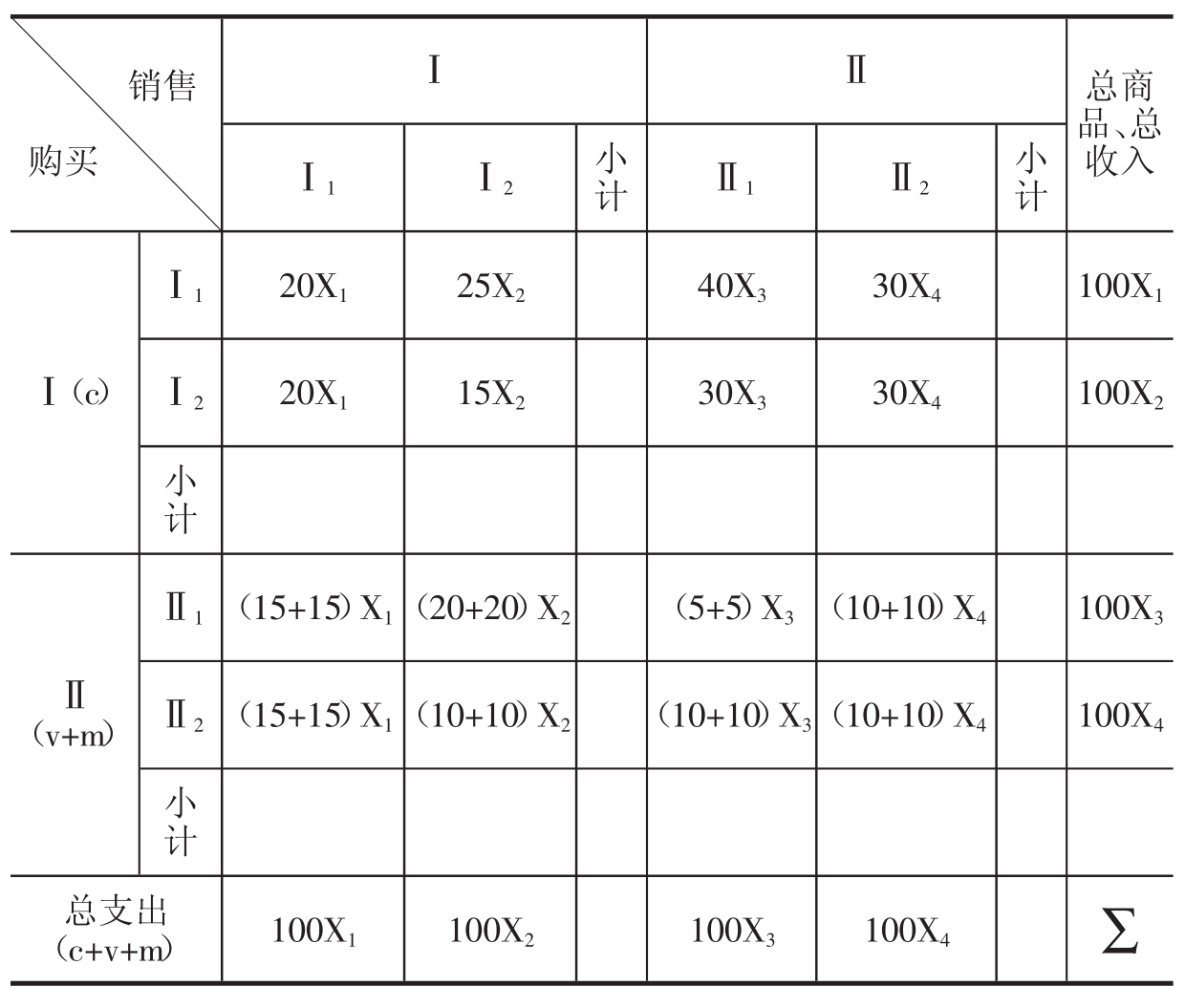
模型是四元线性方程组：

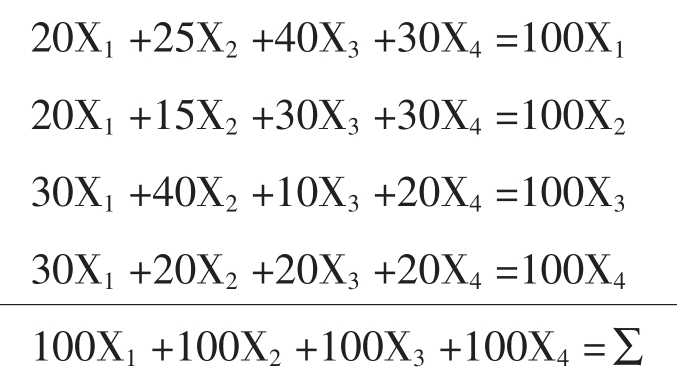
即AX=X

移项，得

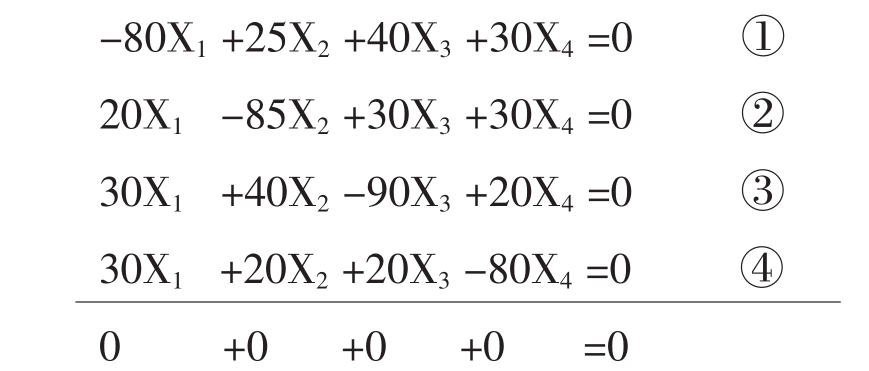
即（I-A）X= 0

因为常数项为0，所以这是一个齐次线性方程组。因为①+②+③+④=0，所以四个方程只有三个是独立的，必有一个是多余的。也就是说，任意三个方程相加，必能推导出剩下的一个来，这个就是多余的。比如，①+②+③=-④，④式是多余的；还有①+②+④=-③，③式是多余的，等等。去掉任意一个多余的方程，解剩下的三元一次方程组，得

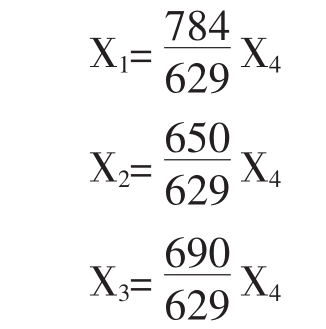
这种方程组有0解和无穷多组非0解。0解无意义。求非0解，可令任意一个X等于任意一个非0值，就可求出任意多个非0解。一般令X₁=1，就可求出X₂、X₃、X₄的相对值来。但求出来的解是分数值（也就是小数值），会有少许误差。为了求整数解，令X₄=629，得

X₁=784

X₂=650

X₃=690

也就是说，X₁：X₂：X₃：X₄=784：650：690：629

将此解代入模型，得表5-2四个分部类的棋盘式平衡表。

表5-2　四个分部类的棋盘式平衡表

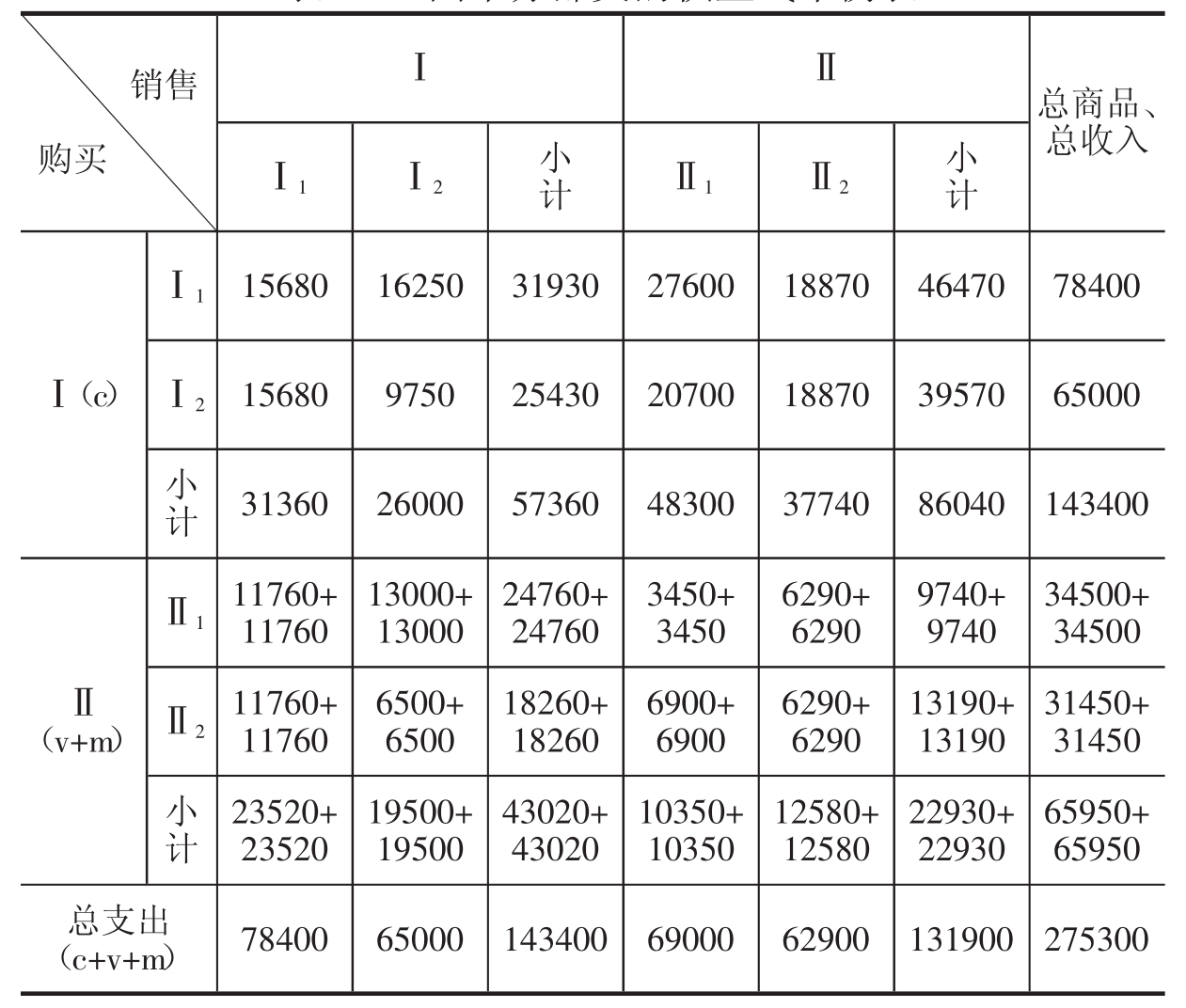
我惊奇地发现，表的纵横是平衡的，当然这是模型中预先设定好的。令我更为惊奇的是Ⅰ（43020v+43020m）竟然=Ⅱ86040c，令我欣喜若狂，这是预先没想到的。这说明我的模型和表与马克思的公式是完全相通的。用公式表示就是:

模型的意义在于把数学引入了再生产理论之中，计算出了两大部类及其分部类的比例关系，强化了定量分析。以前常说正确处理两大部类的比例关系，但正确的比例关系谁也不会计算。

马克思认为：“一种科学只有在成功地运用数学时，才算达到了真正完善的地步。”^[1]再生产理论也应该是这样。马克思虽然精通数学，但没把数学运用到再生产理论之中，以至于人们不能量化两大部类的比例关系。现在，我们把数学运用到再生产理论之中，建立再生产平衡模型，精确地计算两大部类及其各个分部类之间的比例关系。

比例关系比比皆是，著名的黄金分割就是一种比例关系。据说人体的上半身和下半身的长度如果满足黄金分割比，就最匀称优美。

图5-1　达·芬奇：人体黄金分割最美

就像黄金分割一样，四个分部类只有保持X₁誜X₂誜X₃誜X₄= 784誜650誜690誜629这样的比例关系才最佳。

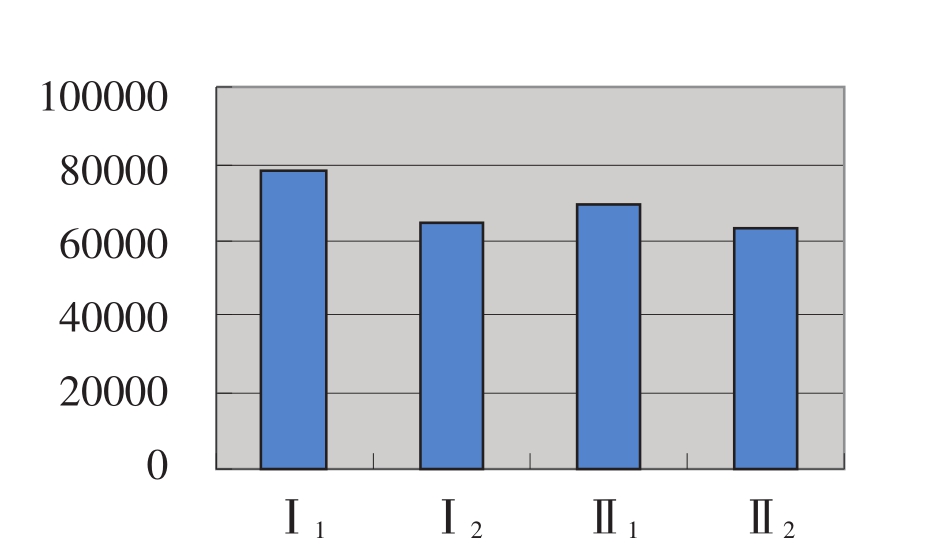
图5-2　杨斌林：四个分部类这种比例最佳