区域创新动力学系统的分解与协调

(二)区域创新动力学系统的分解与协调

1.区域创新系统的分解

系统工程包含着分解与协调技术。该技术及其应用处于整体性原则的支配之下。按照区域创新系统不同的层次或阶段，逐个将组成要素或子系统区分开来进行分析，对于认识整个系统、作出决策以及协调配合的关系极大。在对区域创新系统进行研究的过程中，对该系统的分解贯穿于系统的分析、设计、决策以至系统控制管理的全过程中。

如果就区域创新系统的目标函数而言，该系统可分解成几个子系统，即整体目标可以分散。这是进行系统分解建立数学模型的先决条件。其函数表达式为:

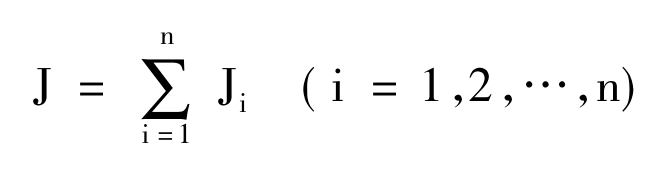
式中: J——区域创新系统的整体目标函数;

　　　J_i——子系统的目标函数。

2.区域创新系统的协调

区域创新系统协调的目的和出发点是整体，但并不等于总体的协调。在对该系统分解的基础上进行的第二步工作，即对各子系统相互作用的全面调节和控制，才是系统的协调。各子系统之间的相互关系可以通过关系矩阵反映出来。在实际问题中的某子系统与其他子系统的直接联系是少量的、有限的，因此关系距阵通常可用分块对角形式来表述。子系统本身是由基本单元、反馈回路组成的。它包括三个基本的变量，即状态变量、速率变量(或称决策变量)和辅助变量。这三个变量可分别由状态方程、速率方程和辅助方程表示。它们与其他一些变量方程、函数和常数一起能描述区域创新系统这样动态、非线性和非时变系统内部的各种变化。

根据系统动力学模型变量和方程的特点，建立区域创新系统内部变量之间总体的数学描述如下:

L= PR

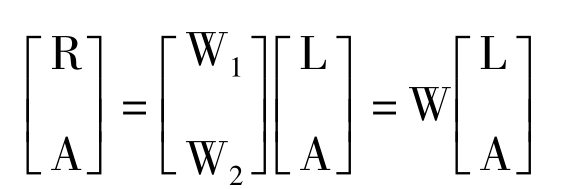
式中: L——状态变量向量;

　　　R——速率变量向量;

　　　A——辅助变量向量;

　　　L——纯速率变量向量;

　　　P——转移矩阵;

　　　W——关系矩阵。

P阵之所以称为转移矩阵，是因为其作用在于把t时刻的速率变量转移到下一个时刻(t+ 1)上去。通常纯速率L仅为各速率R的线性组合，因此一般P阵是个常数项。W之所以称为关系矩阵，因为它反映了变量R和L之间以及A本身在同一时刻的各种非线性关系。显然，在特殊情况下，若系统是线性的，则关系矩阵W为一常数阵。

以上变量表达了因果关系反馈回路中的决策反馈机制。在决策反馈机制中，决策总是根据可收集、获得并应用的信息作出的。决策控制了行动，而行动又影响着区域创新系统的状态，有关系统状态的新情况又促使决策得以修正。