创新应提供较理想的经济价值

第一节　创新应提供较理想的经济价值

我们这里所说的创新，是指企业中的创新。企业的创新活动，可以是指企业产品的更新，也可以是指企业新形象的设计以及企业经营新谋略的制定，还可以是指企业新品牌的策划以及企业管理方法的改革等等。不论是哪一方面的创新，都要以企业能取得较理想的经济价值为基本标准。

为什么要确立这条基本标准？这是由企业自身的性质决定的。什么是企业？《辞海》中对企业作了如下解释：所谓企业，就是指从事生产、流通或服务性活动的独立核算经济单位。从这一解释中，我们首先看到，企业是经济单位。作为经济单位，当然就要讲究经济效益；就要按照经济规律运行；就要进入市场，成为市场活动中的主体，积极参与市场竞争，在竞争中实现优胜劣汰。其次我们看到，企业又是独立核算的单位。这就是说，所有企业都应成为独立的商品生产者和商品经营者。它们自主经营，自负赢亏，自我发展，按经营的效益决定再生产的规模和分配的状况。它们不可能像事业单位那样享受到国家的财政拨款。正是企业的这种特定性质，决定了它们在一切活动中都要算一算经济帐，都要进行严格的经济核算。经济上的长期亏损，就要导致企业的倒闭，这是铁的法则和无情的规律。

企业所以要开展创新活动，就是要使自己在市场竞争中能占据有利地位，能获得更大的市场占有率，能形成不断发展的动力。这一切，最终都要表现为企业能创造出明显的经济效益。由此也就决定了，它们在创新活动中不能不讲究经济价值。

拿产品更新来说。假定某手表厂想要开发一种具有新功能的手表。经过研究试制之后，这种具有新功能的手表确实研制出来了，但是，为取得这种新功能而增加的成本投入，却相当大，从而使具有此新功能的手表，价格过高，失去了市场竞争力。即使投放市场，也会因价格过高而造成积压。这就是一种经济价值不理想的创新，这样的创新是不会得到支持的。如果手表厂还想开发此种具有新功能的手表，他们就必须想方设法降低成本，使价格质量比趋于合理，从而使具有新功能的手表投放市场后，能取得较好的经济效益。

再拿经营谋略来说。任何新的经营谋略，都应是能使企业获取最理想经济效益的谋略。否则，这种所谓的新谋略就是不可取的。在这方面，美国飞机制造业大名鼎鼎的女董事长欧雷芙·比切的经历，就很说明问题。50年代，她的小型飞机订价都在15000美元以上，同行们为了与她竞争，所设计的同类飞机价格都在13000美元左右。为此，公司的研究人员纷纷向欧雷芙献策：我们也可以制造较廉价的飞机。他们一致认为，如果价格降不下来，在销路上一定会吃亏的，在价格上差2—3千美元，当然是个很显著的数字，但在内部结构上的差异却是很微小的，一般不易觉察，所以买便宜货的人就是自然多。这一新提出的制造廉价飞机的谋略能不能采纳呢？欧雷芙笑着明知故问道：“那么，我们为什么不能以现在制造的飞机削价出售呢？”大家一致说：这可不行，我们讲求利润合理，若将现在的产品减价，公司就没有多少钱可赚了。针对此种说法，欧雷芙说：“这就说，一分钱一分货，没有人会做不赚钱的生意，其它公司设计的13000美元的飞机，必定在质量上不如我们。既然东西不一样，那就让我们去制造那种便宜货，我们照高标准的生产方式作业，我们卖的是飞机，不是玩具，不能靠降低质量来求价格的降低。”此时，仍有一些人坚持原先提出的谋略。他们说：“那么，即使我们不放弃现在制造的飞机，至少也该增加廉价的一种，让消费者有个选择。”欧雷芙则很直率地说：“这更不行！这无疑是砸自己的招牌，如果廉价飞机出了毛病，人们会说比切公司的产品质量不好，这样，我们的飞机也没有人要了”。由于欧雷芙的坚持，研究人员放弃了生产廉价品的谋略。后来证实，她的决策非常正确，因为买私人飞机的都是大享，他们重视品质和安全，并不计较那多花的2—3千美元，欧雷芙获得了较理想的经济效益。研究人员提出的新谋略之所以不可取，因为它最终将会毁坏公司的经济效益。如果公司的招牌都被砸了，还有什么经济效益可言？！

怎样才能判断出某项创新是否具有较理想的经济价值？这就需要运用许多决策方法，如期望值分析法，价值工程分析法，等等。所以，为了使创新具有较理想的经济价值，从事或组织创新活动的人们，应该学习一点决策的理论和方法。在此，我们仅对几种最简便易行的方法，作一极简单的介绍。

一、穆迪图表法

穆迪图表法有三种主要类型。第一种称作穆迪简单优先图表法，第二种称为穆迪多目标输入优先图表法，第三种称为穆迪多目标加权优先图表法。我们逐一作出说明。

1．穆迪简单优先图表法

这是某一位思维者或决策者在面对多个创新思路或成果时选择满意思路或成果的一种方法。操作步骤主要有：

第一步，明确当前所要解决的问题。例如，某商场的商品经常被窃，造成经济损失。这种损失如何才能制止？这就是一个需要去解决的问题。

第二步，提出用于解决问题的若干种思路或若干种办法，即提出若干种可能的创新方案（可能的创新点子）。例如，针对上述问题，假定人们提出了如下四种可能的创新方案（四种创新点子）：安装摄像机；增加警卫；重金奖励；雇两个职业小偷。我们对四种可能方案编号，依次为①②③④。这里需要指出，人们总是在一定的环境状态下去选择某一种可能方案（点子）。我们为了叙述方便，暂时不去考虑环境状态问题。

第三步，画出对不同方案进行比较的矩阵图，行与列都标上供选择的可能方案的编号。

第四步，对可供选择的可能方案①②③④进行两两比较，并且规定在每次比较中只能在0与1中取值。0表示该可能方案相对不优越，1表示该可能方案相对优越。我们首先将行上的编号①与列上的编号①②③④逐一比较。由于行①和列①是可能方案①自身与自身相比，无所谓是否相对优越，因此就在第一行第一列的空格中填上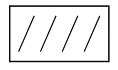。行①与列②相比，实际就是可能方案①与可能方案②相比，如果在这一比较中，决策者或思维者认为②相对优越于①，那么就在第一行第二列的空格中填上0，而在第二行第二列的空格中填上1。行①与列③相比，实际是可能方案①与可能方案③相比，如果在这一比较中，决策者或思维者认为①相对优越于③，那么就在第一行第三列的空格中填上1，而在第三行第一列的空格中填上0。行①再和列④相比，实际是可能方案①和可能方案④相比，如果在这一比较中，决策者或思维者认为④相对优越于①，那么就在第一行第四列的空格中填上0，而在第四行第一列的空格中填上1。这样，行上编号①已与列上编号①②③④逐一比较完毕，也就是说，可能方案①已与可能方案①②③④逐一比较完毕。接着就可将行上编号②与列上编号①②③④逐一比较。行②与列①相比，实际就是可能方案②与可能方案①相比，由于在行①与列②的比较中已有结论，就不再重新比较。行②与列②相比，实际就是可能方案②自身相比，无所谓是否相对优越，因此，就在第二行第二列的空格中填上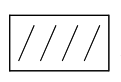。行②和列③相比，实际就是可能方案②③之间相比。如果在这一比较中，决策者或思维者认为③相对优于②，就在第二行第三列的空格中填上0，而在第三行第二列的空格中填上1。行②与列④相比，实际就是可能方案②④之间相比。如果在这一比较中，决策者或思维者认为④相对优越于②，那就在第二行第四列的空格中填上0，而在第四行第二列的空格中填上1。随后，我们再将行上编号③与列上编号①②③④逐一相比。行③与列①相比，实际是可能方案③①之间相比，行③与列②相比，实际就是可能方案③②之间相比，由于在前述比较中已有结论，就不再重复比较。行③与列③相比，实际是可能方案③自身相比，无所谓是否相对优越，因此就在第三行第三列的空格中填上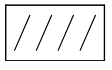。行③与列④相比，实际就是可能方案③④之间相比。如果在这一比较中，决策者或思维者认为④相对优越于③，那么就在第三行第四列的空格填上0，而在第四行第三列的空格中填上1。当我们把行上编号④与列上编号①②③④相比时，由于结论都已产生，就不再重新比较了。

第五步，将每一行所得的值相加，第一行得数为1，第二行第三行得数也为1，第四行得数为3。一般说来，其中得数最高的，即为最可选择的方案。这就是说，在某个决策者或思维者看来，通过运用穆迪简单优先图表法对四种可能方案进行比较，他认为以选择第四种可能方案即选择雇用两名职业小偷的方案为最满意。

2．穆迪多目标输入优先图表法

这是在存在多位决策者（思维者）并且具有同样的决定权的情况下从几个可能方案中选择满意方案的一种方法。操作步骤的前三步都与简单优先图表法相同。从第四步开始，就出现了区别。由于存在多位决策者（思维者）且具有同等权力，所以通过两两比较之后的取值，就不再是只有0与1两种。仍以上例来说明。假定现在有5位具有同等权力的决策者（思维者）需共同作出选择满意方案的决定，然而他们在每次比较中的态度并不相同，于是就出现了如下复杂情况：

我们将行上编号①与列上编号①②③④逐一比较。行①与列①相比，就是可能方案①自身相比，于是我们就在第一行第一列的空格中填上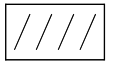。行①与列②相比，就是可能方案①②之间相比。如果在这一比较中，5位决策者（思维者）中有4位认为①相对优越于②，有1位认为②相对优越于①，即有4位把票投给了①，1位把票投给了②，由于他们拥有同等权力，所以，通过比较，我们就在第一行第二列的空格中填上4，而在第二行第一列的空格中填上1。行①与列③相比，实际是可能方案①③之间相比。

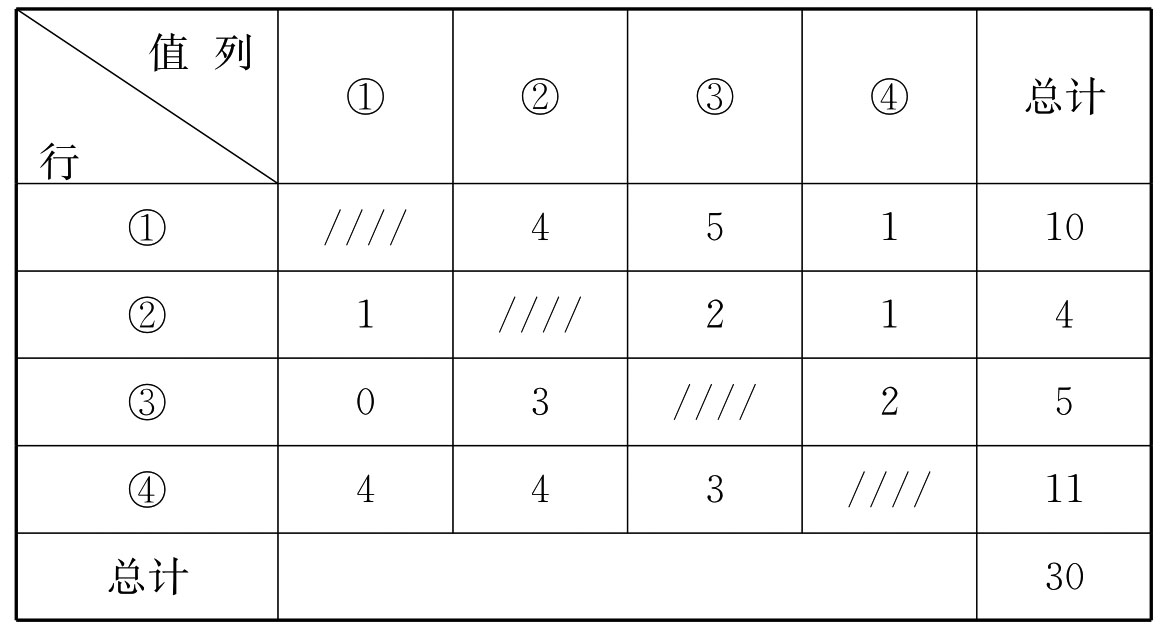
如果在这一比较中，5位具有同等权力的决策者（思维者）都认为①相对优越于③，我们就可在第一行第三列的空格中填上5，而在第三行第一列的空格中填上0。行①与列④相比，实际就是可能方案①④之间相比。如果5位具有同等权力的决策者（思维者）中，有1位认为①相对优越于④，有4位认为④相对优越于①，我们就在第一行第四列的空格中填上1，而在第四行第一列的空格中填上4。按同样道理操作，我们就假定得到了上图中的各种情况。我们把每一行的值相加，其相加的得数分别为10，4，5，11。一般说来，其中得数最高的即为最可选择的满意方案。这就是说，在5位决策者看来，通过运用穆迪多目标输入优先图表法，他们认为以选择雇用两名职业小偷的方案为最满意。

为了检查这种两两比较的结果有无差错，我们一方面可将每一行的得数再相加，在本例中再相加的总和为30；另一方面，我们运用公式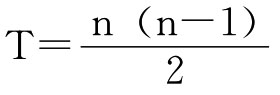（p）进行计算。公式中的n为参与比较的可能方案数，在本例中参与比较的可能方案数为4。公式中的p为每次比较中取值的总数，在本例中共有5位决策者（思维者）参加比较，并他们具有同等权力，因此每次比较时取值的总值数为5。公式中的T为各行得数再相加的总和。将上述值代入公式，于是得T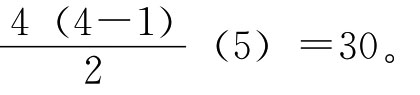＝我们把上述图表中各行得数相加总和与这里通过公式计算所得数相对照，如果它们一致，则说明上述图表无误，如果不一致，就需要对图表进行核对。在本例中，由于它们两者一致，说明图表无误。

3．穆迪多目标输入加权优先图表法

这是在存在多位决策者（思维者）且他们拥有不相等权力的条件下选择满意方案的一种方法，还以上例来说明，假定现有5位决策者（思维者），但他们拥有的权力不等，其中1人拥有3票权力，而其他4人每人只有1票权力。这样，在两两比较中，实际就是对总值7进行分配。如果把下图中行①和列②相比，实际就是可能方案①②之间相比。假定其中3人认为①相对优越于②，而且此3人中有一人拥有三票权，另2人认为②相对优越于①，那么我们就可以在第一行第二列的空格中填上5，而在第二行第一列的空格中填上2。以此类推，我们就可假定得到下图所示情况。

其中第一行相加所得的分值为最高，因而就可认为安装摄像机为可选择的满意方案。我们仍可用上述公式进行检查，由于这里可分配的总值数为7，所以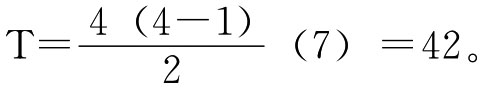，可见我们所建立的上述图表无误。

二、期望值分析法

前面已经指出，人们在提出各种供选择的可能方案（点子）时，总是不能脱离一定的环境条件，人们不是在这种环境条件下去提出和选择可能方案（创新点子），就是在那种环境条件下去提出和选择可能方案（创新点子）。例如，某商场为了解决商品被窃的问题，曾提出了四种可能方案（点子）供选择。他们在提出和选择这些可能方案（点子）时，总是处于一定的客观条件之下，比如，他们或者是处在商场经营状况良好的客观环境条件下，或者是处在商场经营状况日益变坏的客观条件下。这样，某商场就可能在商场经营状况良好的条件下去提出和选择安装摄像机这一方案，也可能在商场经营状况日益变坏的条件下去提出和选择安装摄像机这一方案；可能在商场经营状况良好的条件下去提出和选择雇用两个职业小偷这一方案，也可能在商场经营日益变坏的条件下去提出和选择雇用两个职业小偷这一方案，等等。客观环境条件成为人们在提出和选择可能方案时不可忽视的重要因素。在决策理论中，这种客观环境条件也称作可能状态。对于选择可能方案的决策者（思维者）来说，他可能已经完全确定地了解到某种可能状态一定出现，如果他在此时作出选择，他就是在进行确定型的决策；他也可能无法了解到某种可能状态是否完全确定地出现，但依据以往经验，可以大概地知道某种可能状态有百分之几的可能出现，亦即可以大概地知道某种可能状态出现的概率，如果他在此时作出选择，他就是在进行风险型的决策；他还能不仅无法了解到某种可能状态是否完全确定地出现，而且也不能大概地知道某种可能状态出现的概率，如果他在此时作出选择，他就是在进行不确定型的决策。期望值分析法就是人们在进行风险型决策时可能用来选择满意方案的一种方法。换句话说，期望值分析法就是在已知各可能状态发生的概率的条件下，选择满意方案的一种方法。

我们以E表示期望值，

以a_i（i＝1，2，3……n）表示可能方案变量，S_j（j＝1，2，3……n）表示可能状态变量，

以U_ij（i＝1，2，3……m，j＝1，2，3……n）表示a_i方案在S_j状态下的效用。所谓效用，就是指某一方案在某种状态下所获得的值，

以P（S_j）（j＝1，2，3……n）表示S_j状态的概率，

则期望值分析法可用如下公式表示：

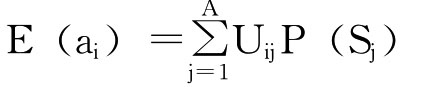
从受益角度说，我们取期望值最大的方案为可选择的满意方案，从受损角度说，我们取期望值最小的方案为可选择的满意方案。现举一实例加以说明，某企业新开发一种产品，如何才能把新产品推销出去？针对这一问题，假定人们出了两个不同的点子，亦即提出了两个可能方案，一个是大做广告（我们用a₁表示），一个是不做广告（我们用a₂表示）。人们总是在一定的环境条件下提出和选择某种方案。假定未来的环境条件可以表现为两种可能状态，一是市场比较景气（我们用S₁表示），一是市场比较不景气（我们用S₂表示）。经过测算，如果选择第一个点子（方案），那么在市场比较景气的可能状态下，第一年便可获纯收益500万元，而在市场比较不景气的可能状态下，第一年则要支付50万元广告费，还要再加上日常维持费10万元，即要损失60万元；如果选择第二个点子（方案），那么在市场比较景气的可能状态下，第一年可获利300万元，而在市场比较不景气的可能状态下，虽不支付广告费，但仍要支付日常维持费10万元，即要损失10万元。根据以往经验并经管理人员共同研究，人们得知市场比较景气出现的概率P（S₁）＝0．3，市场比较不景气出现的概率P（S₂）＝0．7，运用决策模型，可得下图：

E（a₁）＝（500×0．3）＋（60×0．7）＝108万元

E（a₂）＝（300×0．3）＋（－10×0．7）＝83万元

由此我们看到，从受益角度分析，a₁方案（点子）提供的期望值要比a₂方案（点子）大得多，尽管市场比较景气这种可能状态出现的概率仅为0．3，我们仍选择a₁方案（点子）为满意方案（点子）。

我们再举一例说明。某冰棍厂在年初要制订未来六、七、八三个月的生产计划。根据当时已知材料可知，每销售一箱冰棍，可获利50元，每积压一箱冰棍，每天反而要支付冷藏保管费30元，或者说获利为－30元。所以，如果生产计划订低了，就要减少盈利，如果订高了，出现积压，就要受到损失。究竟应如何安排生产计划才比较合适？这就是需要解决的问题。假定管理者发动人们出主意，最后形成了每天可计划生产100箱，110箱，120箱，130箱四种可能方案（可供选择的点子），同时又总结以往经验得知，在未来六、七、八三个月中，每天实际能售出100箱这种可能状态出现的概率为0．2，每天实际能售出110箱这种可能状态出现的概率为0．4，每天实际能售出120箱这种可能状态出现的概率为0．3，每天实际能售出130箱这种可能状态出现的概率为0．1，运用决策模型，可得下图：

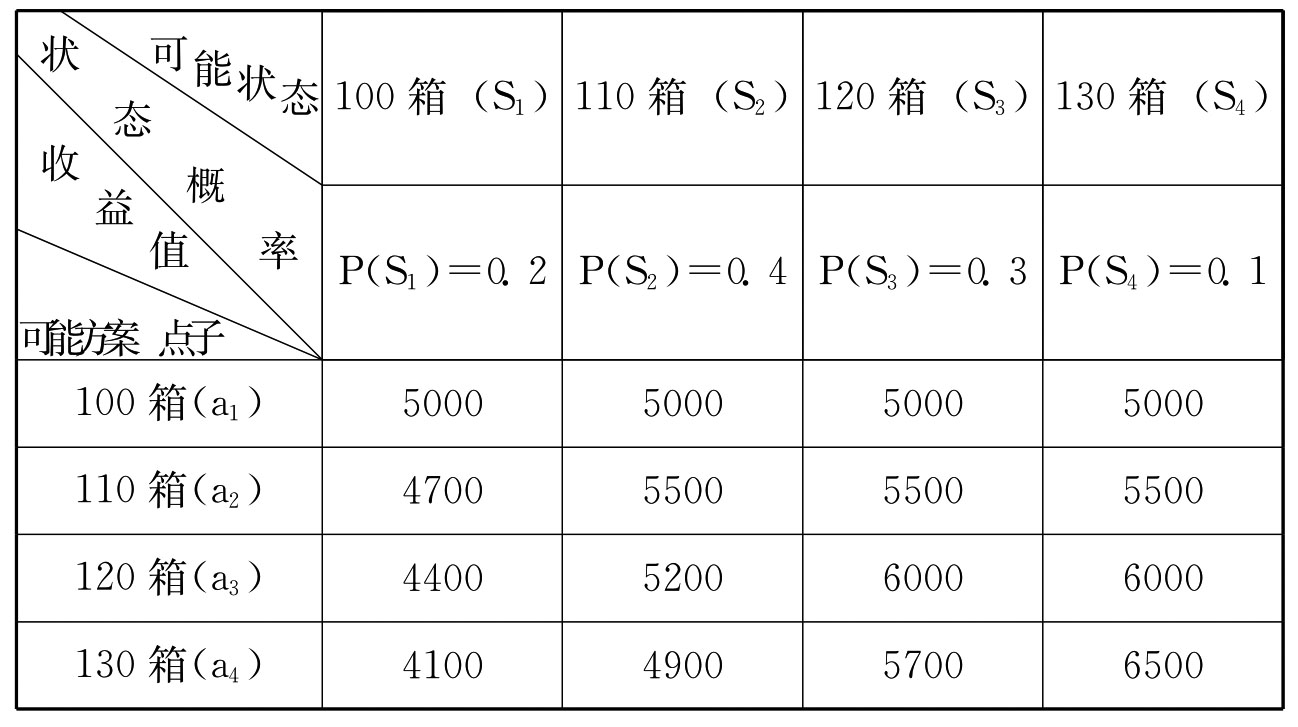
运用期望值公式，可知：

E（a₁）＝（5000×0．2）＋（5000×0．4）＋（5000×0．3）＋（5000×0．1）＝5000元

E（a₂）＝（4700×0．2）＋（5500×0．4）＋（5500×0．3）＋（5500×0．1）＝5340元

E（a₃）＝（4400×0．2）＋（5200×0．4）＋（6000×0．3）＋（6000×0．1）＝5360元

E（a₄）＝（4100×0．2）＋（4900×0．4）＋（5700×0．3）＋（6500×0．1）＝5140元

我们看到，在考虑到各种可能状态出现的概率的条件下，以a₃方案（点子）提供的收益期望值为最大，我们便可在四种方案（点子）中以选择每天准备产生120箱的a₃方案（点子）为满意方案（点子）

三、最大最小收益值分析法

此方法也叫小中取大法，这是针对不确定型决策而采用的方法。

在人们对不同方案（点子）进行选择时，最理想的情况当然是从各个方案在各种不同的可能状态下产生的收益值中，选择能带来最大收益值的方案（点子）。但是，这种可能带来最大收益值的方案（点子），或者较难实现，或者风险较大。因此，一些人往往愿意采取一种较稳妥的办法，即求出各方案（点子）在各种状态下的最小收益值，然后从各种最小收益值中选择其中具有最大值的方案（点子）。这就是最大最小收益值分析法。

例如，某商店在经过整顿之后，为了能在新年度中打一个翻身仗，提出了a₁a₂a₃a₄四种可供选择的方案（点子），并且经过分析，估计会遇到S₁S₂S₃S₄四种可能状态。这种可能状态是完全不确定的，通过对销售额，资金周转率利润率等进行测算，得到各方案（点子）在不同可能状态下的收益值如下：

由此可以看到，a₁方案（点子）在S₁S₂S₃S₄四种可能状态下的收益值分别为700，650，350，200，其中以200为最小收益值；a₂方案（点子）以400为最小收益值；a₃方案（点子）以300为最小收益值，a₄方案（点子）以250为最小收益值。比较四种方案的最小收益值，其中以400为各最小收益值中的最大者。我们就选择能带来各最小收益值中最大值的a₃方案（点子）为满意方案。（点子）

四、最小最大后悔值分析法

此方案也叫大中取小法。这也是针对不确定决策而采用的方法。前一方法是从收益的角度来分析，本方法则换了一个角度，从后悔方面来分析。所谓后悔，就是指在我们没有选择能带来最大收益值的方案（点子）而选择了其他方案（点子）的情况下，假定能带来最大收益值的方案又恰好能实现，这时我们就会由于没有选择能带来最大收益值的方案而感到受损失，这种损失就是后悔。仍以上例来分析。

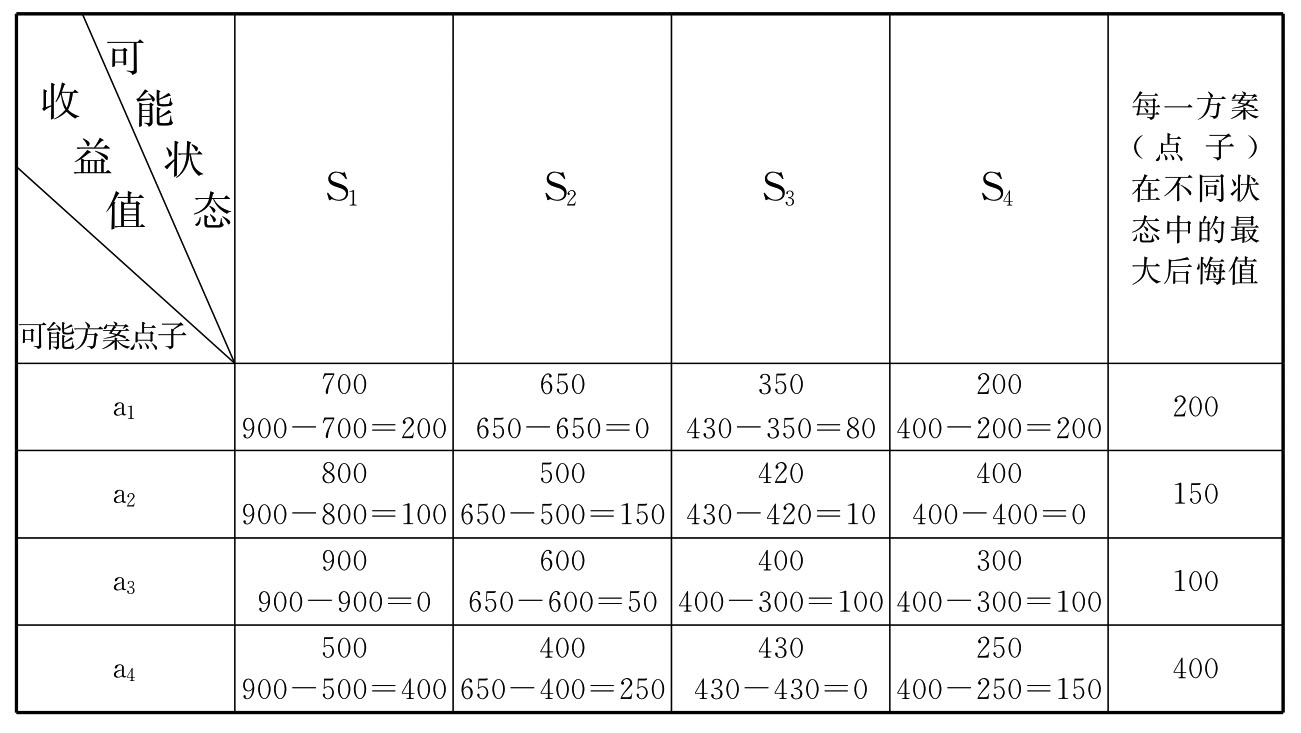
我们先计算出每一方案在不同状态下的收益值。如a₁方案在S₁可能状态下的收益值为700，在S₂可能状态下的收益值为650，在S₃，S₄可能状态下的收益值分别为350，200；a₂方案在S₁S₂S₃S₄可能状态下的收益值分别为800，500，420，400等等。

我们再计算出在每种可能状态下不同方案的后悔值。在S₁可能状态下，a₁方案的收益值为700，a₂的收益值为800，a₃的收益值为900，a₄的收益值为500，其中以a₃方案的收益值900为最大。假定在S₁可能状态下，我们没有选择a₃方案而选了a₁方案，就会感到后悔，其后悔值为900－700＝200；假定在S₁可能状态下，我们没有选择a₃方案而选了a₂方案，其后悔值为900－800＝100；假定在S₁可能状态下我们恰好选择了a₃，则不后悔，即后悔值为900－900＝0；假定我们在S₁可能状态下没有选a₃而选了a₄，后悔值就为900－500＝400，其余以此类推。

我们接着比较每一方案在不同可能状态下的后悔值，选出其中的最大的后悔值。a₁方案在S₁S₂S₃S₄四种可能状态下的后悔值分别为200，0，80，200，其中以200为a₁方案的最大后悔值。同理，我们找出a₂方案的最大后悔值为150，a₃的最大后悔值为100，a₄的最大后悔值为400。

最后，我们比较不同方案的最大后悔值，即比较200，150，100，400，从中选出最小者，即100。这样，能带来最大后悔值中最小后悔值的方案，就是可以选择的满意方案（点子）。在本例中，a₃方案（点子）就是能带来最大后悔值中最小后悔值的方案（点子），因而a₃方案（点子）就是可以选择的满意方案（点子）。

五、折衷收益值分析法

在选择满意决策方案（满意点子）时，有人愿意选择收益值最大，然而风险也最大的方案（点子），有人则愿意选择收益值虽最小，然而风险也最小的方案（点子），但是，也有人既不愿冒最大风险去获取最大收益值，也不愿意在风险最小情况下只获得最小收益值，而是愿意采取一个介于两者之间的折衷性方案。此时就需运用折衷收益值分析法。

我们以m表示折衷系数，并且假定收益值最小风险也最小的方案（点子）的折衷系数m＝0，收益值最大风险也最大的方案（点子）的折衷系数m＝1，那么可选择的折衷性方案（点子）的折衷系数m_a应在0与1之间，即0＜m＜1。如果我们在选择方案（点子）时，愿意向收益较大风险也较大的方向倾斜，那么折衷系数就可能向1靠近；如果我们在选择方案（点子）时，愿意向收益较小风险也较小的方向倾斜，那么折衷系数就可以向0靠近。我们再以X₁表示最大收益值，以X₂表示最小收益值，则折衷收益值E_a可用如下公式表示：

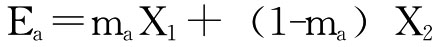
我们还用前例来说明，通过测算和分析，可得出各方案（点子）的最大收益值和最小收益值如下：

现在，我们假定把折衷系数选择为0．7，即愿意冒稍大一些风险但也不想风险太大，则运用上述公式可得各方案（点子）的折衷收益值如下：

E_a1＝0．7×700＋（1－0．7）×200＝550

E_a2＝0．7×800＋（1－0．7）×400＝680

E_a3＝0．7×900＋（1－0．7）×300＝720

E_a4＝0．7×500＋（1－0．7）×250＝425

此时，我们就可选取能带来最大折衷收益值的方案（点子）即a₃方案（点子），为满意方案（点子）。这里非常关键的一环，在于决策者（思维者）如何去确定折衷系数。这是需要决策者（思维者）根据自己所掌握的材料并根据自己的利益标准和行为准则作出主观断定的。如果折衷系数发生变化，那么所选择的满意方案（点子）也就可能发生变化。例如，假定决策者（思维者）把折衷系数定为0．4，即他希望风险性相对更小些，而保险性相对更大些，则上述各方案的折衷收益值分别为：

E_a1＝0．4×700＋（1－0．4）×200＝400

E_a2＝0．4×800＋（1－0．4）×400＝560

E_a3＝0．4×900＋（1－0．4）×300＝540

E_a4＝0．4×500＋（1－0．4）×250＝350

这就是说，当决策者（思维者）愿意在风险性相对地更小些，而保险性相对地更大些的情况下去选择方案（点子），则根据折衷收益值的计算，可选择a₂方案为满意方案（点子）。

选择满意方案（点子）的方法还有很多，我们就不再多作介绍了。