几种常见工程情况下的朗肯主动土压力计算

几种常见工程情况下的朗肯主动土压力计算_地质与岩土力学基

情景10　土压力

【学习目标】

1.了解土压力的概念和类型。

2.掌握三种土压力的发生条件。

3.掌握静止土压力的概念和计算方法。

4.掌握朗肯土压力理论及其在各种情况下的土压力计算方法。

5.理解库仑土压力理论。

6.掌握土压力的应用—挡土墙的设计。

【能力要求】

1.能够阐述土压力的概念和类型以及发生的条件。

2.能够利用朗肯土压力理论完成在各种情况下的土压力计算。

3.能够初步完成简单重力式的设计。

【必要的理论知识与资料】

10.1　概述

挡土墙是用来支撑天然或人工斜坡的稳定，或使部分侧向荷载传递分散到填土上的一种土工结构物，其作用就是挡住墙后的土体(土坡或填土)，防止土体坍塌和失稳。在水利、水电、港口、航道以及房屋建筑等工程建设中，常需修筑挡土墙。因此挡土墙必须承受来自墙后土体的侧向压力，称为土压力。在挡土墙的设计中，土压力是作用于挡土墙的外荷，土压力大小的计算也是挡土墙设计的主要依据。

在挡土墙横断面中，与被支承土体直接接触的部位称为墙背;与墙背相对的、临空的部位称为墙面;与地基直接接触的部位称为基底;与基底相对的、墙的顶面称为墙顶;基底的前端称为墙趾;基底的后端称为墙踵。

(1)根据其刚度及位移方式不同，可分为刚性挡土墙、柔性挡土墙和临时支撑

刚性挡土墙:本身变形极小，发生失稳时挡土墙只能发生整体位移。如图10－1几种形式挡土墙。

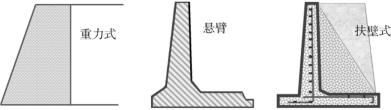
图10－1　常见挡土墙的型式

如墙后土压力过大，墙会整体向前发生移动如图10－2(a)所示;如基地发生沉降，墙会整体发生下沉或倾斜，如图10－2(b)所示;墙后土压力分布如图10－2(c)。

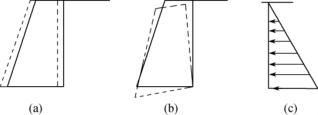
图10－2　挡土墙位移变化简图

柔性挡土墙:当挡土墙结构物自身在土压力作用下发生挠曲变形时，则结构变形将影响土压力的大小和分布，称这种类型的挡土墙结构为柔性挡土墙。发生失稳时挡土墙本身会发生明显的变形，此时墙上土压力分布比较复杂。例如，在深基坑开挖中，为支护坑壁而打入土中的板桩墙即属于柔性挡土墙。这时作用在墙身上的土压力为曲线分布。如图10 －3，实线为实测土压力，虚线为计算土压力。

临时支撑:是指在进行基坑或边坡作业时，为了防止土体失稳，采取措施支住土体，使施工得以继续进行的一种暂时的支护方式。其支撑后的土压力分布受施工过程和变位条件的影响，如图10－4。

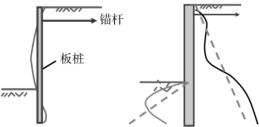
图10－3　柔性挡土墙图示

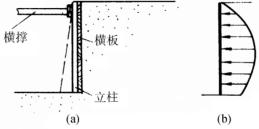
图10－4　临时支撑图示

(2)根据挡土墙的设置位置不同，分为路肩墙、路堤墙、路堑墙和山坡墙等。设置于路堤边坡的挡土墙称为路堤墙;墙顶位于路肩的挡土墙称为路肩墙;设置于路堑边坡的挡土墙称为路堑墙;设置于山坡上，支承山坡上可能坍塌的覆盖层土体或破碎岩层的挡土墙称为山坡墙。

10.2　土压力的性质与影响因素

以刚性挡土墙为重点，讨论挡土墙上的土压力性质及土压力计算，包括土压力的大小、方向、分布及合力作用点。

刚性挡土墙土压力的性质与大小，取决于墙的位移方向与大小。太沙基通过挡土墙模型试验，观测墙在向前、向后产生位移的过程中承受土压力的情况变化，由试验结果得出，当墙身向离开填土方向产生位移时，土压力随之减小至一最小值，如图10－5中a点所示;当墙身向填土方向位移时，土压力随之增大至一最大值，如图10－5中c点所示;墙身无位移时，土压力介于二者之间，如图10－5中b点所示。由此可知，按墙位移情况，有如下三种特定的土压力:

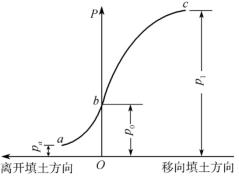
图10－5土压力变化

(1)静止土压力。

若挡土墙静止不动，墙后土体处于弹性平衡状态时(如图10－6)，土对墙的水平压力称为静止土压力，用P0表示，如图10－7。静止土压力可能存在于某些建筑物支撑的土层中，如地下室外墙、地下水池侧壁、涵洞侧墙和船闸边墙等都可近似视为受静止土压力作用。静止土压力可按直线变形体无侧向变形理论求出。

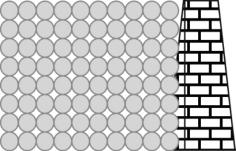
图10－6　静土压力的产生

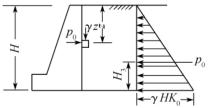
图10－7　静土压力分布图

设在填土表面下任意深度Z处取一单元体，如上图所示，其上作用有竖向的土自重应力σs=γ·Z，则该处的静止土压力强度p0即为土的侧向应力σsx，按式(10.1)计算:

式中　γ——土的重度，kN/m3;

　　　k0——静止土压力系数(即土的侧向压力系数)，无因次。

k0可通过室内或原位静止侧向压力试验测定。在设计中，若无试验资料，经验值:砂土k0=0.34～0.45，粘性土k0=0.5～0.7。对于无粘性土和正常固结粘土，也可用半经验公式计算:

式中　φ'——墙后填土的有效内摩擦角。

若墙后填土为均质时，由(10.1)可知，P0与Z成正比，沿墙高H呈三角形分布。总静止土压力E0为:

式中　H——墙高，m;

　E0的作用点在距墙底处，方向水平，指向墙背。

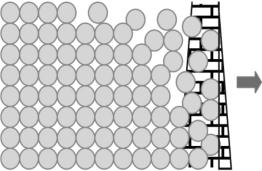
图10－8　主动土压力的产生

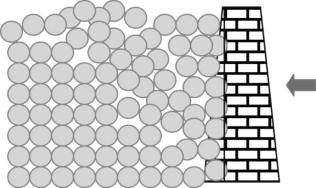
图10－9　被动土压力的产生

(2)主动土压力。

在墙后土体作用下挡土墙以远离土体的方向发生移动，使墙后土体产生“主动滑移”并达到极限平衡状态，此时作用在墙背上的土压力称为主动土压力，用Pa表示，如图10－8。土体内相应的应力状态称为主动极限平衡状态。

(3)被动土压力。

受外力作用挡土墙被迫发生向墙后土体方向的移动并致使墙后土体达到极限平衡状态，此时作用在挡土墙上的土压力称为被动土压力，用Pp表示。土体内相应的应力状态称为被动极限平衡状态(图10－9)。

由挡土墙与墙身位移之间的关系图10－5可以看出，主动土压力值最小，被动土压力值最大，静止土压力值则介于两者之间。

10.3　朗肯土压力理论

朗肯土压力理论是土压力计算中两个最有名的经典理论之一，由英国学者朗肯于1857年提出。它是根据半空间的应力状态和土的极限平衡条件而得出的土压力计算方法。由于其概念清楚，公式简单，便于记忆，目前在工程中仍得到广泛应用。

10.3.1　朗肯土压力理论中的基本假设

朗肯土压力理论认为:作用在垂直墙背上的土压力，相当于达到极限平衡(主动或被动状态)时的半无限体中任一垂直截面上的应力，即作用在挡土墙垂直墙背AB(图10－10(a))上的土压力，也就是达到极限平衡时半无限体中和墙背AB方向相符的AA'切面上AB段(图10－10(b))的应力。朗肯认为在满足一定的条件下，可用挡土墙代替半无限土体的一部分，而不影响土体其他部分的应力情况。这样，朗肯土压力理论作为极限问题只取决于一个边界条件，即半无限体的界面情况。对于较简单的假设界面:

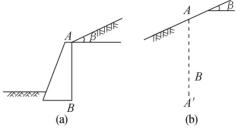
图10－10　朗肯土压力基本假设

①挡土墙墙背直立;

②墙后土体表面水平;

③墙背光滑。

以上三种情况下土压力，可采用朗肯土压力理论较方便地求解。

由上述的简单界面条件出发可得，墙背因光滑与土体没有摩擦力;墙后土体表面水平，故土体竖直面和水平面没有剪应力，因此竖直方向和水平方向的应力为主应力，竖直方向的应力即为土的竖向自重应力。根据上述分析，按墙身的移动情况，由墙后土体

内任一点处于主动或被动极限平衡状态时大小主应力间的关系求得主动或被动土压力强度及其合力。

当挡土墙不发生偏移，土体处于静止状态时，距地表z处M点的应力状态见图10－11 (a)和(d)中应力圆Ⅰ。此时M单元水平截面上的应力等于该处土的自重应力，竖向截面上的法向应力是该点处土的静止土压力。由于该点未达到极限平衡状态，故应力圆Ⅰ在强度线以下。

如果由于某种原因使土体在水平方向伸展或压缩，使土体由弹性平衡状态转为塑性平衡状态，土中应力状况将发生变化。

若土体在水平方向伸展，则M单元在水平截面上的法向应力不变而竖直截面上的法向应力却逐渐减少，直至满足极限平衡条件(主动朗肯状态)，此时M点水平向应力σx达到最低极限值pa。因此，pa是小主应力，竖向应力σz为大主应力，该点莫尔圆与抗剪强度线相切，如图10－11(b)和(d)。

若土体在水平方向受到压缩，则水平向应力σx不断增加而竖向应力σz保持不变，直到满足极限平衡条件(被动朗肯态)时σx达最大极限值pp，这时pp是大主应力而σz是小主应力，莫尔圆为图10－11(d)中的圆Ⅲ，也与抗剪强度线相切。

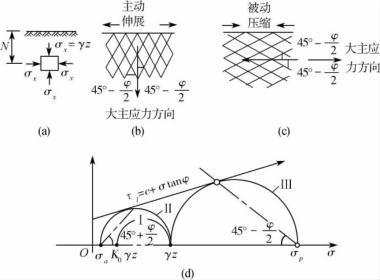
图10－11　半空间的极限平衡状态

(a)半空间的单元体;(b)半空间的主动朗肯状态; (c)半空间的被动朗肯状态;(d)莫尔圆表示主动和被动朗肯状态

土体处在主动朗肯状态时水平截面为大主应力作用面，剪切破裂面与水平面成(45° +φ/2)角度(图10－11(b))。当土体处在被动朗肯状态时，水平截面为小主应力作用面，此时剪切破裂面与水平面成(45°－φ/2)，见图10－11(c)。

10.3.2　朗肯土压力理论的计算原理

当地面水平时，土体内任一竖直面都是对称面，因此竖直和水平截面上的剪应力等于零，相应截面上的法向应力σz和σx都是主应力。当墙后土体达到极限平衡状态时，可应用土体处于极限平衡状态时大、小主应力间的关系式来计算作用于墙背上的土压力。

(1)主动土压力。

根据前述分析，当墙后填土达到主动极限平衡状态时，作用于任意深度z处土单元的竖直应力σz=γh应是大主应力σ1，作用于墙背的水平向土压力pa应是小主应力σ3。由土的强度理论可知，当土体中某点处于极限平衡状态时，大主应力σ1和小主应力σ3间满足以下关系式:

以σ3=pa，σ1=γz代入式(10.4)，即得朗肯主动土压力计算公式为

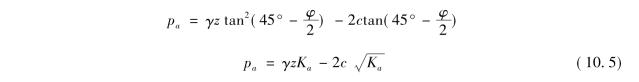
式中　Ka—主动土压力系数，Ka=tan2(45°－);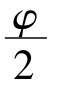

　γ—墙后填土的重度(kN/m3)，地下水位以下取浮容重;

　c—填土的黏聚力(kPa);

　φ—填土的内摩擦角;

　z—计算点距填土面的深度(m)。

以σ3=pa，σ1=γz代入式(10.6)，即得朗肯主动土压力计算公式为

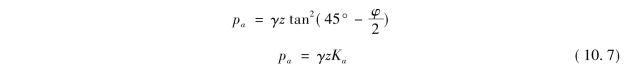
式中　Ka—主动土压力系数，Ka=tan2(45°－);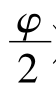

　γ—墙后填土的重度(kN/m3)，地下水位以下取浮容重;

　φ—填土的内摩擦角;

　z—计算点距填土面的深度(m)。

由式(10.7)可知，无黏性土的主动土压力强度与深度z成正比，沿墙高压力分布为三角形，如图10－12(b)所示，作用在墙背上的主动土压力的合力Ea即为pa分布图形的面积，其作用点位置在分布图形的形心处，土压力作用方向为水平，即

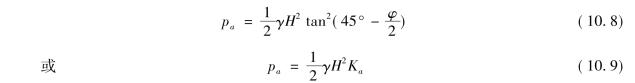
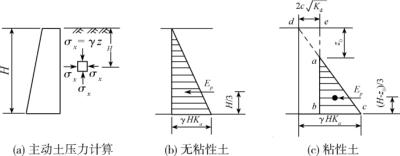
图10－12　主动土压力强度分布图

由式(10.5)可知，黏性土的朗肯土压力强度包括两部分:一部分是由土自重引起的土压力γzKa，另一部分是由黏聚力c引起的负侧向压力2c 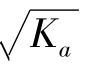，这两部分压力叠加的结果如图10－12(c)所示，其中ade部分是负侧压力，意为对墙背是拉应力，但实际上墙与土在很小的拉力作用下就会分离，因此在计算土压力时，这部分拉力应略去不计，黏性土的土压力分布仅为abc阴影面积部分。

a点离填土面的距离z0常称为临界深度，可由式(10.5)中令pa=0求得z0值，即:

则单位墙长黏性土主动土压力pa为

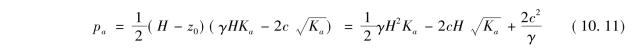
主动土压力pa通过三角形压力分布图abc的形心，即作用在离墙底(H－z0)/3处，方向水平。

(2)被动土压力。

当墙体在外力作用下向土体方向移动并挤压土体时，土中竖向应力σz=γz不变，而水平向应力σz却逐渐增大，直至出现被动朗肯状态，如图10－13所示。此时，作用在墙面上的水平压力达到极限pp，为大主应力σ1，而竖向应力σz变为小主应力σ3。可得被动土压力强度计算公式

以σ1=pp，σ3=γz代入式(10.12)，即得朗肯被动土压力计算公式为

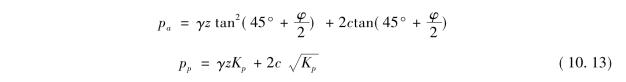
式中　Kp——被动土压力系数，Kp=tan2(45+);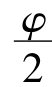

　γ——墙后填土的重度(kN/m3)，地下水位以下取浮容重;

　c——填土的黏聚力(kPa);

　φ——填土的内摩擦角;

　z——计算点距填土面的深度(m)。

以σ1=pp，σ3=γz代入式(10.14)，即得朗肯被动土压力计算公式为

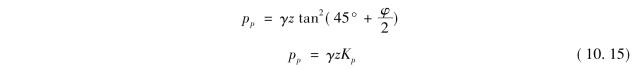
式中　Kp—被动土压力系数，Kp=tan2(45+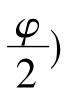φ2 )

　γ—墙后填土的重度(kN/m3)，地下水位以下取浮容重;

　φ—填土的内摩擦角;

　z—计算点距填土面的深度(m)。

由上面两式可知，黏性土被动土压力随墙高呈上小下大的梯形分布，如图10－13(c);无黏性土的被动土压力强度呈三角形分布，见图10－13(b)。被动土压力Pp的作用点通过梯形压力或三角形压力分布图的形心，作用方向水平。

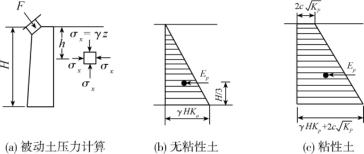
图10－13　被动土压力强度分布图

单位墙长被动土压力合力为:

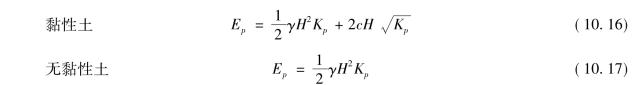
注:对于具有倾斜土体表面的挡土墙土压力，也可采用朗肯土压力理论进行求解。其推导思路与土体表面水平时类似，只是在分析时需要把水平地表面半无限体中一点的应力状态改为分析具有倾斜表面的半无限体中一点的应力状态，求出达到极限平衡状态时的应力条件，即可得出作用于倾斜土体表面、竖直墙背上的土压力

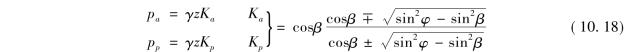
上式中β为土体表面倾角。从上式可知，土压力为线性分布，方向与土面平行。

从上可见，朗肯土压力理论与计算公式相对简单，使用方便。但由于在推导过程中所采取的假定条件和简化，使该理论使用范围受限。例如，由于朗肯理论忽略了墙背与土体之间的摩擦作用，即不计强土之间的摩擦角影响，从而使计算的主动土压力偏大，被动土压力偏小。

从上述朗肯土压力公式还可看出，只要掌握了黏性土土压力的有关公式，从这些公式容易推出无黏性土的相应公式，即令黏性土土压力公式中的c=0就可得出无黏性土公式。

现场填土施工质量也影响土压力的大小。若通过加强工程措施，提高施工质量，使填土的抗剪强度指标c、φ值增加，将有助于减小主动土压力和增加被动土压力。

【例题10.1】有一高度为6m、墙背光滑、竖直的挡土墙，墙后填土表面水平且与墙同高(图10－14)。填土的物理力学性质指标如下:γ=16kN/m3，φ=20°，c=10kN/m2。试用朗肯土压力公式求主动土压力Ea。

【解】主动土压力系数

对于粘性土，墙背拉力范围临界深度z0=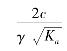，即

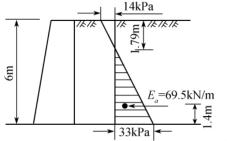
图10－14　例题1土压力计算图

由朗肯主动土压力公式(7－5)，有

墙顶　pa=γzKa－2c×0.7=－14kPa＜0，故pa=0kPa

墙后　z0=1.79m处，pa=0kPa

墙底　pa=γzKa－2c =16×6.0×0.49－2×10×0.7=33kPa

据此可绘出墙背土压力的分布如图10－15。

土压力合力为应力分布图面积，即

Ea作用方向水平，作用点距墙底×(6.0－1.79)=1.4m处。

10.4　几种常见工程情况下的朗肯主动土压力计算

工程中经常遇到土面有超载、分层填土、填土中有地下水的情况，当挡土墙满足朗肯土压力简单界面条件时，仍可根据朗肯理论按如下方法分别计算其土压力。

10.4.1　墙后填土水平表面上有连续均布荷载时

当墙后填土面作用有连续均布荷载时，则均布荷载通过土体对墙背产生附加的土压力，如图10－15所示。由于连续均布荷载的作用，在土体中任一点均增加一个竖向应力分量Δpt=q，则在深度为Z处的竖向应力为:

σz=γz+q

当填土为无粘性土(c=0kPa)时，作用于距墙顶深度为Z处的主动土压力强度为:

pa=　(　γz+q)ka

墙顶面Z=0处主动土压力强度为:

pa=qka。

作用在墙背上的主动土压力为梯形分布，总主动土压力为:

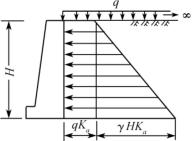
图10－15　墙后有均布荷载土压力计算图

当填土为粘性土时，作用于距墙顶深度为Z处的主动土压力强度为:

墙顶面Z=0处主动土压力强度为:

(1)当墙顶面处土压力大于粘聚强度时(qka＞2c作用在墙背上的主动土压力为梯形分布，总主动土压力为:

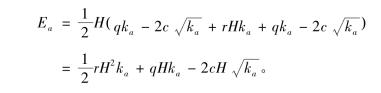
(2)当墙顶面处土压力小于粘聚强度时(qka＜2c)，墙顶处的土压力为负，可认为此时土压力pa=0，在墙顶下某处z0点，其土压力理论值pa=0，可计算该点距离墙顶处深度为:

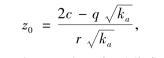
则作用于墙后主动土压力自z0点以下为三角形分布，总主动土压力为:

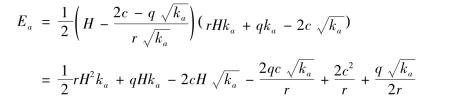
Ea作用方向水平，作用点距墙底(H－z0)处。

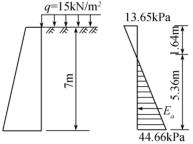
图10－16　例题10.2土压力计算图

【例题10.2】某现场有一挡土墙，墙高7m，墙背垂直光滑，填土顶面水平并与墙顶同高。填土为黏性土，主要物理力学指标为:γ=17kN/m3，φ=20°，c=15kPa，在填土表面上作用连续均布超载q=15kPa。试求主动土压力大小及其分布(图10－16)。

【解】在填土表面处的主动土压力强度pa为

=15×0.49－2×15×0.7=－13.65kPa

临界深度z0可由pa=0条件求出，即

令paz=0，有

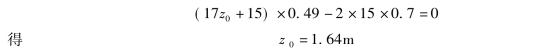
墙底处:

pa7=(17×7+15)×0.49－2×15×0.7=65.66－21=44.66kPa

土压力强度分布图如图10－17所示。

主动土压力的合力Ea为土压力强度分布图形中阴影部分的面积，即

合力作用点距离墙底距离为×(7－1.64)=1.79m。

10.4.2　墙后填土内有地下水位

当墙后填土内有地下水位时，将会产生以下三个方面的影响:

(1)水位以下土的重度减小为浮重度;

(2)抗剪强度有所降低;

(3)水对墙背施加了静水压力。总效果是使墙背所受的侧压力增大。在这种情况下，作用在墙背上的侧压力有土压力和静水压力两部分，计算土压力时，一般假设地下水位上下土的内摩擦角φ不变。

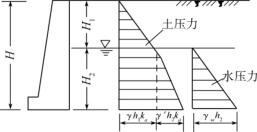
图10－17　墙后填土有地下水位土压力计算图

当墙后填土为无粘性土时，图10－17中，地下水位以上H1深度内为湿重度γ，水位以下H2深度内为浮重度γ'。地下水面处的主动土压力强度为:

pa'=γH1ka。

墙底面处土压力强度为:

总土压力为折线压力分布图形的面积。在H2深度内的静水压力为:

【例题10.3】求图10－18所示挡土墙的主动土压力。墙后填土因排水不良，地下水位距墙底以上2m，填料为砂土，重度γ=18kN/m3，饱和重度γsat=20kN/m3，内摩擦角φ= 30°(假定其值在水位以下不变)。

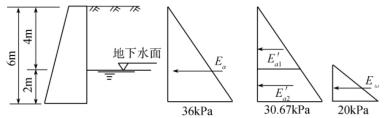
图10－18　例题3土压力计算图

【解】墙后填土有地下水位时，地下水位以上部分按常规方法计算，土压力强度不受地下水影响，但地下水以下的填土需考虑地下水时填土重度的影响。

在墙顶　pa0=0

在墙顶下4m　pa4=γztan2(45°－ )=18×4×tan2(45°－ )=24kPa

在墙底　pa6=[18×4+(20－10)×2]tan2(45°－ )=92× =30.67kPa

主动土压力强度分布如图7－18，主动土压力合力Ea为土压力强度分布图面积之和，即

作用在墙背上的水压力呈三角形分布，合力为该分布图的面积，即

作用在墙上的总侧压力为土压力和水压力之和，即

讨论:若没有地下水，则在墙底:

墙背主动土压力合力:

将此结果与上述有地下水情况对比不难得出:当墙后有地下水时，土压力部分将减小，但计入墙后水压力后，墙背承受的总侧向压力将增大，而且水位越高，总侧压力越大。可见做好墙后填土的排水工作，对减少挡土墙的受力、减少墙后土体软化、保证挡土墙的稳定非常重要。

10.4.3　墙后为成层土时

当墙后为成层土时(图10－19)。各层土的重度γ及强度指标各不相同，应分别确定各层土作用于墙背的土压力，然后叠加而得总土压力。具体计算步骤如下:

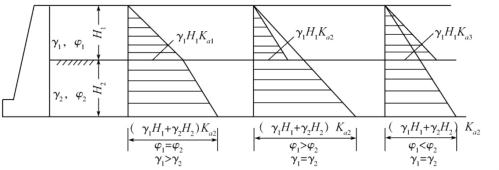
图10－19　填土为成层土土压力计算图

(1)计算各土层交界处的垂直压力

pz=∑γiHi

计算各土层分界面处上、下土层的土压力强度

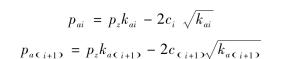
式中　kai、ci——分别为第I分界面上层土的主动土压力系数及凝聚力;

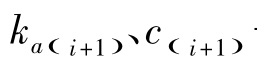——分别为第I分界面下层土的主动土压力系数及凝聚力。

(2)绘出土压力分布图。

(3)计算总土压力，土压力分布图的面积即为总土压力。

【例题10.4】有一挡土墙高6m，墙后填土分为三层，各层土的物理力学性质指标如图10－20所示，试求此分层填土的主动土压力及分布。

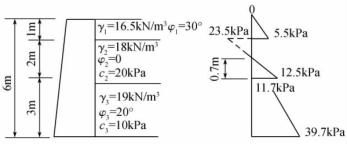
图10－20　例题4土压力计算图

【解】分层填土时可分层计算土压力。首先将土层分界面处的土压力值计算出，然后根据同一土层内土压力线性分布的特点，得到土压力沿墙身的分布，土压力合力就是这些土压力分布图形的面积，合力作用位置可按工程力学中求面积矩的原理求得。具体计算土压力时，对任一层的上覆土层的自重压力可近似地视为作用在该层表面上的连续均布荷载。

在墙顶，z=0，有

在墙顶下1m处，z1=1，有

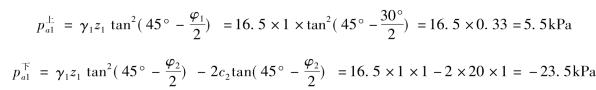
在墙顶下3m处，z2=3，有

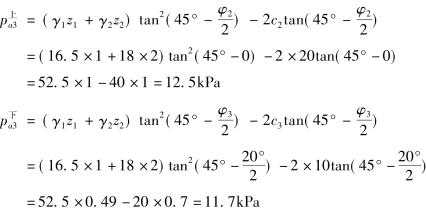
在墙顶下6m处，z3=6，有

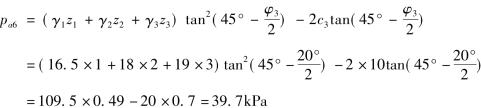
墙背承受的主动土压力强度分布图形见图7－21所示。

不计墙背和填土间的拉应力，则得主动土压力Ea为

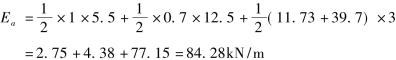
若设合力Ea距墙底为x，则

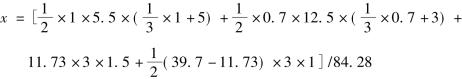
=(14.67+14.15+52.79+41.96)/84.28=1.47m

即Ea作用位置距墙底1.47m，方向水平。

10.5　库伦土压力理论

10.5.1　库伦土压力原理与假设

库伦土压力理论研究的课题(图10－21):

(1)墙背俯斜，倾角为ε(墙背俯斜为正，反之为负);

(2)墙背粗糙，墙与土间摩按角为δ;

(3)填土为理想散粒体，粘聚力c=0;

(4)填土表面倾斜，坡角为β

根据墙后填土达到极限平衡状态时，通过墙踵产生一破裂面BC，如图10－22所示，土体ABC沿破裂面BC及墙背AB随墙的位移有向下或向上滑动的趋势，称为滑动楔体。由滑动楔体上的静力平衡条件，直接导出作用于墙背上的总土压力。当墙身向前(离开填土方向)发生位移，滑动楔体则有向下滑动的趋势，以致达到主动极限平衡状态，这时，墙背上所受的土压力为主动土压力。当墙身向后(填土方向)发生位移，滑动楔体受到挤压，则有向上滑动的趋势，以致达到被动极限平衡状态，这时滑动土体作用在墙背上的阻力即为被动土压力。

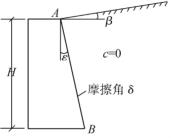
图10－21　库伦土压力挡土墙

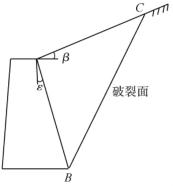
图10－22　墙后填土极限平衡状态

在分析过程中，假设滑动面为一平面，滑动楔体处于极限平衡状态，视滑动体为刚体，墙体是刚性的，填土为无粘性土。

10.5.2　库伦主动土压力

取达到主动极限平衡状态的滑动楔体ABC为脱离体，作用在脱离体上的力有图10－23(a):

(1)滑动楔体ABC的自重W，大小为ABC面积乘单位厚度乘土的重度，方向铅直向下。

(2)滑动面BC上的反力R，作用方向与BC法线方向成φ角，向上(φ为土的内摩擦角)。

(3)墙背对土楔体的反力P，作用方向与墙背法线方向成δ角，向上(δ为墙背面与土体之间的摩擦角，称外摩擦角)。

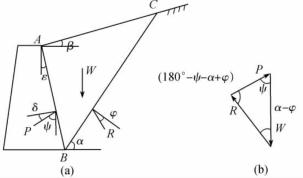
图10－23　按库伦理论求主动土压力

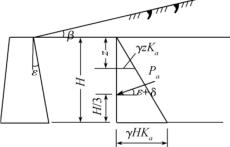
图10－24　库伦主动土压力分布图

滑动土体ABC在上述三个力作用下处于平衡状态，P、W、R三个力构成封闭力矢三角形(图10－23(b))。按正弦定理得:

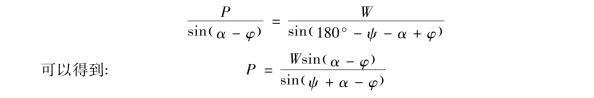
其中　ψ=90°－δ－ε。

由上式可见，若假定不同的滑动面BC，即改变α角，则有不同的W值，亦即P为α角的函数。由图10－23可知，当α=90°+ε时，即BC与AB重合，W=0，P=0。又当α=φ时，R与W方向相反，P=0。故式中P随α改变，P只有一个最大值;与此最大值Pmax方向相反，大小相等，作用在墙背上的力即为所求的总主动土压力Pa。

式中对P关于α求一次导数，并令其等于零，即=0，求得α值，再代回得:

式中:ka——库伦主动土压力系数，为φ、ε、β、δ的函数。

从式中可知，Pa为墙高H的二次函数，若对Pa关于深度Z求一次导数，即得深度Z处的土压力强度:

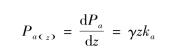
由上式可知，Pa(z)沿深度成三角形分布，如图10－24所示。Pa的作用点距墙底处，方向与水平面成(ε+δ)角。

【例题10.5】图10－25所示挡土墙高5m，填土面倾斜角β=20°，填土重度γ= 17.6kN/m3，φ=30°，c=0，外摩擦角δ=15°。试求主动土压力及作用点，并绘出土压力分布图。

【解】由δ=15°，φ=30°，β=20°，ε=10°查表得主动土压力系数ka=0.535.

墙底处土压力强度Pa=γHka=17.6×5×0.535=47.1kPa。

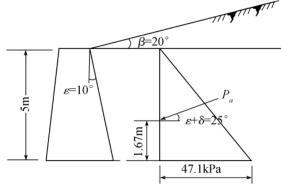
图10－25　例题5土压力分布图

土压力作用点距墙底=1.67m，作用方向与水平面成(ε+δ)角，即25°。

土压力分布示于图10－25中。

10.5.3　库伦被动土压力

墙身受到外力作用向填土方向发生位移，使填土受到挤压作用而达到被动极限平衡状态时，滑动土楔体将沿某一滑动面及墙背面向上滑动，如图10－26(a)所示。此时滑动楔体ABC上作用的力有:

(1)滑动楔体的自重W，方向竖直向下;

(2)滑动面BC上的反力R，与BC法线方向成φ角;

(3)墙背面上的反力R，与墙背法线方向成δ角向下。

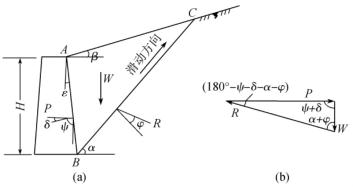
图10－26　库伦被动土压力的计算

土楔体在上述三个力作用下处于平衡，其封闭力矢三角形如图10－26(b)。若假定不同的滑动面BCi(即改变α角)，则有不同的Pi值，其中最小的Pmin值为被动土压力值。原因是当填土受到挤压，必然沿着产生最小P值的滑动面滑动，此滑动面称为最危险滑动面。

与求主动土压力的原理相同，由力矢三角形可得:

式中　ψ=90°－δ。

令=0，求得α代回上式得:

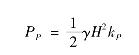
式中:kP——称为被动土压力系数，为φ、ε、β的函数。

与主动土压力相似，土压力强度沿墙高呈三角形分布，方向与墙背法线成δ角向上，总被动土压力作用点在距墙底H/3处。

10.6　挡土墙设计

10.6.1　挡土墙形式的选择

(1)挡土墙选型原则。

①挡土墙的用途，高度与重要性;

②建筑场地的地形与地质条件;

③尽量就地取材，因地制宜;

④安全而经济。

(2)常用的挡土墙型式。

①重力式挡土墙。

重力式挡土墙其特点是体积大，靠墙自重保持稳定性。墙背可做成俯斜，直立和仰斜三种，一般由块石或素混凝土材料砌筑，适用于高度小于6m，地层稳定开挖土石方时不会危及相邻建筑物安全的地段。其结构简单，施工方便，能就地取材，在建筑工程中应用最广(图10－27)。

②悬臂式挡土墙。

悬臂式挡土墙其特点是体积小，利用墙后基础上方的土重保持稳定性。一般由钢筋混凝土砌筑，拉应力由钢筋承受，墙高一般小于或等于8m。其优点是能充分利用钢筋混凝土的受力特点，工程量小(图10－28)。

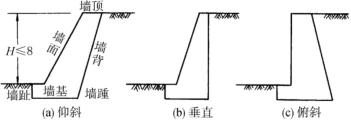
图10－27　重力式挡土墙

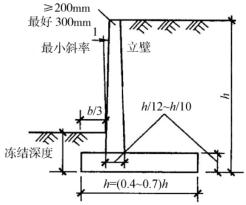
图10－28　悬臂式挡土墙初步设计

③扶壁式挡土墙。

扶壁式挡土墙其特点是为增强悬臂式挡土墙的抗弯性能，沿长度方向每隔(0.8～1.0) h做一扶壁。由钢筋混凝土砌筑，扶壁间填土可增强挡土墙的抗滑和抗倾覆能力，一般用于重大的大型工程(图10－29)。

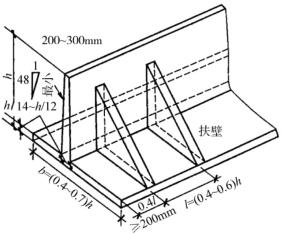
图10－29　扶臂式挡土墙初步设计

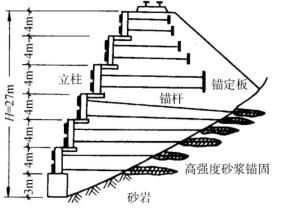
图10－30　锚钉板、锚杆式挡土墙

④锚定板及锚杆式挡土墙。

锚定板及锚杆式挡土墙如图10－30所示，一般由预制的钢筋混凝土立柱，墙面，钢拉杆和埋置在填土中的锚定板在现场拼装而成，依靠填土与结构相互作用力维持稳定，与重式挡土墙相比，其结构轻，高度大，工程量少，造价低，施工方便，特别适用于地基承载力不大的地区。

⑤加筋式挡土墙。

加筋式挡土墙由墙面板，加筋材料及填土共同组成　如图10－31所示，依靠拉筋与填土之间的摩擦力来平衡作用在墙背上的土压力以保持稳定。拉筋一般采用镀锌扁钢或土工合成材料，墙面板用预制混凝土板。墙后填土需要较高的摩擦力，此类挡土墙目前应用较广。

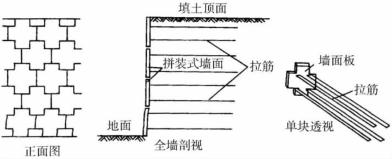
图10－31　加筋式挡土墙

10.6.2　重力式挡土墙设计

(1)重力式挡土墙截面尺寸设计。

挡土墙的截面尺寸一般按试算法确定，即先根据挡土墙所处的工程地质条件、填土性质、荷载情况以及墙身材料、施工条件等，凭经验初步拟定截面尺寸。然后进行验算。如不满足要求，修改截面尺寸，或采取其他措施。挡土墙截面尺寸一般包括:

①挡土墙高度h。

挡土墙高度一般由任务要求确定，即考虑墙后被支挡的填土呈水平时墙顶的高度。有时，对长度很大的挡土墙，也可使墙顶低于填土顶面，而用斜坡连接，以节省工程量。

②挡土墙的顶宽和底宽。

挡土墙墙顶宽度，一般块石挡土墙不应小于400mm，混凝土挡土墙不应小于200mm。底宽由整体稳定性确定。一般为0.5～0.7倍的墙高。

(2)重力式挡土墙的计算。

重力式挡土墙的计算内容包括稳定性验算，墙身强度验算和地基承载力验算(图10－32)。

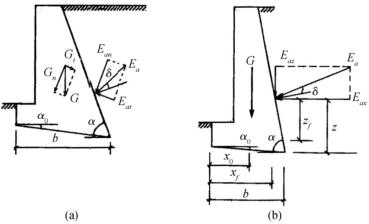
图10－32　挡土墙稳定性验算

①抗滑移稳定性验算。

在压力作用下，挡土墙有可能基础底面发生滑移。抗滑力与滑动力之比称为抗滑移安全系数Ks，Ks按下式计算:

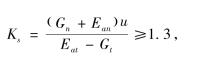
式中　G——为挡土墙每延米自重;

　　　α0——为挡土墙基底的倾角;

　　　α——为挡土墙墙背的倾角;

　　　δ——为土对挡土墙的摩擦角;

　　　u——为土对挡土墙基底的摩擦系数。

若验算结果不满足要求，可选用以下措施来解决:

a.修改挡土墙的尺寸，增加自重以增大抗滑力;

b.在挡土墙基底铺砂或碎石垫层，提高摩擦系数，增大抗滑力;

c.增大墙背倾角或做卸荷平台，以减小土对墙背的土压力，减小滑动力;

d.加大墙底面逆坡，增加抗滑力;

e.在软土地基上，抗滑稳定安全系数较小，采取其他方法无效或不经济时，可在挡土墙踵后加钢筋混凝土拖板，利用拖板上的填土重量增大抗滑力;

②抗倾覆稳定性验算。

如图10－32所示为一基底倾斜的挡土墙，在主动土压力作用下可能绕墙趾向外倾覆，抗倾覆力矩与倾覆力矩之比称为倾覆安全系数Kt，Kt按下式计算。

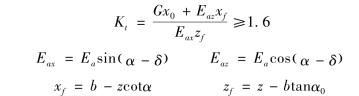
式中　z——土压力作用点离墙基的高度;

　　　x0——挡土墙重心离墙趾的水平距离;

　　　b——基底的水平投影宽度。

挡土墙抗滑验算能满足要求，抗倾覆验算一般也能满足要求。若验算结果不能满足要求，可伸长墙前趾，增加抗倾覆力臂，以增大挡土墙的抗倾覆稳定性。

③整体滑动稳定性验算，可采用圆弧滑动方法。

④地基承载力验算。

挡土墙地基承载力验算，应同时满足下列公式

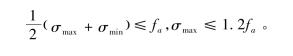
另外，基底合力的偏心距不应大于0.2倍基础的宽度。

⑤墙身材料强度验算，与一般砌体构件相同。

(3)重力式挡土墙的构造。

在设计重力式挡土墙时，为了保证其安全合理、经济，除进行验算外，还需采取必要的构造措施。

①基础埋深。

重力式挡土墙的基础埋深应根据地基承载力，冻结深度，岩石风化程度等因素决定，在土质地基中，基础埋深不宜小于0.5m;在软质岩石地基中，不宜小于0.3m。在特强冻胀、强冻胀地区应考虑冻胀影响。

②墙背的倾斜形式。

当采用相同的计算指标和计算方法时，挡土墙背以仰斜时主动土压力最小，直立居中，俯斜最大。墙背倾斜形式应根据使用要求。地形和施工条件等因素综合考虑确定。应优先采用仰斜墙。

③墙面坡度选择。

当墙前地面陡时，墙面可取1∶0.05～1∶0.2仰斜坡度，亦采用直立载面。当墙前地形较为平坦时，对中，高挡土墙，墙面坡度可较缓，但不宜缓于1∶0.4。

④基底坡度。

为增加挡土墙身的抗滑稳定性，基底可做成逆坡，但逆坡坡度不宜过大，以免墙身与基底下的三角形土体一起滑动。一般土质地基不宜大于1∶10，岩石地基不宜大于1∶5。

⑤墙趾台阶。

当墙高较大时，为了提高挡土墙抗倾覆能力，可加设墙趾台阶，墙趾台阶的高宽比可取h∶a=2∶1，a不得小于20cm。(如图10－33所示)

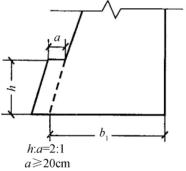
图10－33　墙趾尺寸设计

⑥设置伸缩缝。

重力式挡土墙应每间隔10～20m设置一道伸缩缝。当地基有变化时，宜加设沉降缝。在挡土结构的拐角处，应采取加强构造措施。

⑦墙后排水措施。

挡土墙因排水不良，雨水渗入墙后填土，使得填土的抗剪强度降低，对产生挡土墙的稳定不利的影响。当墙后积水时，还会产生静水压力和渗流压力，使作用于挡土墙上的总压力增加，对挡土墙的稳定性更不利。因此，在挡土墙设计时，必须采取排水措施。

载水沟:凡挡土墙后有较大面积的山坡，则应在填土顶面，离挡土墙适当的距离设置载水沟，把坡上径流载断排除。载水沟的剖面尺寸要根据暴雨集水面积计算确定，并应用混凝土衬砌。载水沟出口应远离挡土墙，如图10－34(a)所示。

泄水孔:已渗入墙后填土中的水，则应将其迅速排出。通常在挡土墙设置排水孔，排水孔应沿横竖两个方向设置，其间距一般取2～3m，排水孔外斜坡度宜为5%，孔眼尺寸不宜小于100mm。泄水孔应高于墙前水位，以免倒灌。在泄水孔入口处，应用易渗的粗粒材料做滤水层，必要时作排水暗沟，并在泄水孔入口下方铺设粘土夯实层，防止积水渗入地基不利墙体的稳定。墙前也要设置排水沟，在墙顶坡后地面宜铺设防水层，如图10－34(c)所示。

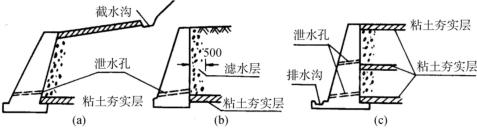
图10－34　挡土墙排水设施

⑧填土质量要求。

挡土墙后填土应尽量选择透水性较强的填料，如砂、碎石、砾石等。因这类土的抗剪强度较稳定，易于排水。当采用粘性作填料时，应掺入适当的碎石。在季节性冻土地区，应选择炉碴、碎石、粗砂等非冻结填料。不应采用淤泥，耕植土，膨胀土等作为填料。

【例题10.6】已知某块石挡土墙高6m，墙背倾斜ε=10°，填土表面倾斜β=10°，土与墙的摩擦角δ=20°，墙后填土为中砂，内摩擦角φ =30°，重度γ=18.5kN/m3。地基承载力设计值fa= 160kPa。设计挡土墙尺寸(砂浆块石的重度取22km/ m3)。

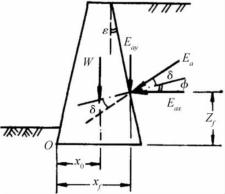
图10－35　例题6挡土墙示意图

解(1)初定挡土墙断面尺寸:

设计挡土墙顶宽1.0m底宽4.5m如图10－35所示，墙的自重为

G==363kN/m

因α0=0，Gn=363kN/m，Gt=0kN/m

(2)土压力计算:

由φ=30°、δ=20°、ε=10°、β=10°，应用库仑土压力理论

得Ka=0.438，由公式(5－16)得，

Ea的方向与水平方向成30°角，作用点距离墙基2m处。

Eax=Eacos(　δ+ε)=145.9×cos(20°+10°)=126.4kN/m

Eaz=Easin(　δ+ε)=145.9×sin(20°+10°)=73kN/m

因α0=0，Ean=Eaz=73kN/m

Eat=Eax=126.4kN/m

(3)抗滑稳定性验算:

墙底对地基中砂的摩擦系数u，查表得μ=0.4。

抗滑安全系数满足要求。

(4)抗倾覆验算:

计算作用在挡土墙上的各力对墙趾O点的力臂

自重G的力臂x0=2.10m

Ean的力臂xf=4.15m

Eax的力臂zf=2m

抗倾覆验算满足要求。

(5)地基承载力验算:

作用在基础底面上总的竖向力

N=Gn+Eaz=363+73=436kN/m

合力作用点与墙前趾O点的距离

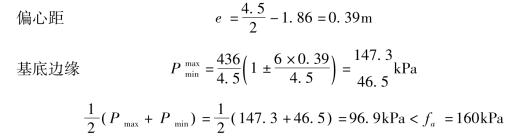
Pmax=147.3kPa＜1.2fa=1.2×160=196kPa

地基承载力满足要求。

因此该块石挡土墙的断面尺寸可定为:顶宽1.0m，底面4.5m，高6.0m。

【思考题】

1.土压力按产生条件分为哪几种?

2.影响土压力大小的因素有哪些?其中最重要的影响因素是什么?

3.何谓静止土压力?如何计算及适用范围?

4.产生主动土压力的条件是什么?适用于什么范围?

5.什么是被动土压力?什么条件下产生?工程中如何应用?

6.朗肯土压力理论的假设条件有哪些?适用于什么范围?土压力系数如何计算?

7.库伦土压力研究的课题是什么?有何基本假设?适用于什么范围?

8.朗肯土压力理论与库伦土压力理论有什么区别?

9.挡土墙有哪几种类型?各自有何特点?

10.重力式挡土墙设计步骤有哪些?

11.挡土墙设计中要进行哪些验算?

【练习题】

1.某重力式挡土墙高5.8m，墙后填土面水平，墙背垂直、光滑。其物性指标为:C= 10kPa，φ=20°，γ=17.0kN/m3;

(1)试绘出墙背上主动土压力沿墙高的的分布图;

(2)试求作用在墙背的总主动土压力的合力。

2.某挡土墙高H=6m，墙背竖直、光滑、墙后填土表面水平。填土为干砂，容重γ= 18kN/m3，内摩擦角φ=30°计算:

(1)作用在挡土墙上的静土压力;

(2)若墙能向前移动，要向前移动多少距离才能产生主动土压力?并计算主动土压力大小?

3.某挡土墙高8m，墙后填土面水平，墙背垂直、光滑。作用在填土面上的大面积均布荷载q=30kPa，墙后填土为粘性土，其物性指标为:C=15kPa，φ=30°，γ=19.0kN/m3。

计算作用在墙背的总主动土压力的合力并绘出墙背上主动土压力沿墙高的的分布图。

4.某挡土墙高H=6m，墙背竖直、光滑、墙后填土表面水平。填土为干砂，容重γ=18kN/m3，内摩擦角φ=30°，墙后填土中的地下水在距墙顶2m处，砂土的饱和重度为γsat=21.0kN/m3，求此时挡土墙所受的静土压力、主动土压力及水压力。

5.已知某一挡土墙高5m，墙背竖直、光滑、墙后填土表面水平，填土分为2层，第一层为砂土:C=0kPa，φ=30°，γ1=18.0kN/m3，第二层为粘性土:C=10kPa，φ=20°，γ2=19.0kN/m3。

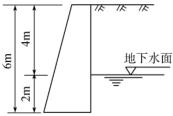
图10－36　习题6图

计算该挡土墙后的主动土压力并绘出土压力分布图。

6.已知某挡土墙高6m，地下水位在距墙低2m处，墙背竖直、光滑、墙后填土表面水平，墙顶宽1.5m，墙低宽3.3m，墙低与地基的摩擦系数为0.4，墙体材料的平均重度为29.0kN/m3，验算此挡土墙的抗滑稳定性及抗倾覆稳定性(图10－36)。