1 绪 论
1.1 测量学的任务和在国民经济建设中的应用
测量学主要研究对象是地球局部地区内的地形信息的采集、处理与应用和工程设计施工定位的基本理论、技术与方法。它的主要任务包括测定和测设两个部分。测定是指使用测量仪器设备和工具,通过测量采集得到一系列地球表面空间点位的几何数据和属性信息,经过计算处理与整理,把地球表面的地形缩绘成地形图,供经济建设、规划设计、科学研究和国防建设使用;测设是指在实施工程建设的规划、管理和设计时,需要将图纸上规划设计好的建筑物、构筑物的位置在地面上标定出来,作为施工的依据。
测量学在国民经济和社会发展规划中应用很广,测绘信息是最重要的基础信息之一。在城市规划、市政工程、工业厂房与民用建筑等工作中有着广泛的应用。例如:在工程勘测设计的各个阶段,要求有各种比例尺的地形图,供城镇规划、厂址选择、管道和交通线路选线以及总平面图设计和竖向设计之用。在施工阶段,要将设计的建筑物、构筑物的平面位置和高程测设于实地,以便进行施工。施工结束后,还要进行竣工测量,绘制竣工图,供日后扩建和维修之用。即使是竣工以后,对某些大型及重要的建筑物和构筑物还要进行变形观测,以保证建筑物的安全使用。
在铁路、公路、桥梁和隧道建设中,要选择确定一条经济合理的线路和地址,需要预先测绘选址线路上条带状地形图,在地形图上进行线路设计,然后将设计好的线路位置标定在实际地面上,用以指导工程施工;当线路跨越河流时,需建设桥梁,对建设桥梁的河流区域需要测绘地形图,供桥位选择、桥台和桥墩位置确定使用;当线路穿过山岭时需要开挖隧道,开挖前,应在地形图上确定开挖隧道的位置,根据设计和测量数据确定其开挖的长度和方向,保证正确贯通。
另外,在城市建设中的房地产开发、管理与经营中,在国土资源和地籍调查中,在各项工农业基本建设中,从勘测设计阶段到施工、竣工阶段,都需要进行大量的测绘工作。在国防建设中,军事测量和军用地图是现代大规模的诸兵种协同作战不可缺少的重要保障。至于要导弹命中目标,除了应测算出发射点和目标点的精确坐标、方位和距离外,还必须掌握地球形状、大小的精确数据和有关地域的重力场资料。在空间科学技术的研究,地面沉降、山体滑坡变形的研究,救灾和突发事件应急等方面,都要应用测绘资料。在国家的各级政府管理工作中,测量和地图资料也是不可缺少的重要工具。
1.2 测绘科学定义及发展概况
1.2.1 测绘科学的定义与研究内容
随着测绘科学技术的发展和应用领域的扩大,近代的测绘学已发展为一门综合学科,它在一系列测绘新技术和新设备的帮助下,能够解决许多复杂的科学、技术与工程问题。
现代科技条件下的测绘学,是研究测定和推算地面及其外层空间点的几何位置,确定地球形状,获取地表自然形态和人工设施的几何分布及属性,并缩绘成图的学科。现代测绘学主要研究地球空间信息的采集,并具有信息处理、管理、更新等过程,是地球科学的一个分支学科。
测绘学科根据研究的重点内容和应用范围来分类,包括以下几门主要学科:
1)大地测量学
大地测量学是研究地球形状、大小和变化,测定地球表面广大地区点的位置及地球重力场的理论和方法的学科。近年来,因人造地球卫星的发射和科学技术的发展,大地测量学又分为常规大地测量学和卫星大地测量学。
2)摄影测量学
摄影测量学是利用摄影像片来测定物体的形状、大小和空间位置的一门学科。根据获得像片方式的不同,摄影测量学又可分为地面摄影测量学、航空摄影测量学、水下摄影测量学和航天摄影测量学等。
3)海洋测绘学
海洋测绘学是以海洋水体和海底为研究对象所进行的测量理论、方法和海图编制工作的一门学科。
4)工程测量学
工程测量学是研究工程建设和自然资源开发各个阶段中的各种测量工作的一门学科。
5)地图制图学
地图制图学是研究地图及其编制和应用的一门学科。随着计算机技术引入地图制图中,出现了计算机地图制图技术。
1.2.2 测绘科学发展概况
测绘学是一门历史悠久的科学,早在几千年前,由于当时社会生产发展的需要,中国、埃及、希腊等国家的人民就开始创造与运用测量工具进行测量。测量工作一开始是用于土地整理。古埃及尼罗河洪水泛滥,水退之后两岸土地重新划分时,已经有了测量工作。我国汉代司马迁在《史记》“夏本纪”中就有叙述公元前22—前21世纪时禹治理洪水、开发国土时“左准绳,右规矩,载四时,以开九州,通九州,陂九泽,度九山”,北宋时期,我国就发明了指南针,以后又创制了浑天仪等测量仪器,并绘制了相当精确的全国地图。指南针于中世纪由阿拉伯人传到欧洲,以后在全世界得到广泛应用,到今天仍然是利用地磁测定方位的简便测量工具。我国古代劳动人民为测量学的发展做出了重要的贡献。
随着社会生产力的发展,测量逐渐应用到社会的许多生产部门。17世纪发明望远镜后,人们利用光学仪器进行测量,使测量科学迈进了一大步。自19世纪末发展了航空摄影测量后,又使测量学增添了新的内容,现代光学及电子学理论在测量中的应用,创制了一系列激光、红外光、微波测距、测高、准直和定位的仪器。惯性理论在测量学中的应用,又创制了陀螺定向、定位仪器。20世纪60年代以来,由于电子计算技术的飞速发展,出现了自动化程度很高的电子水准仪、电子经纬仪、电子全站仪和自动绘图仪等。人造地球卫星的成功发射,使其很快就被应用于大地测量,自1957年前苏联第一颗人造地球卫星发射成功后,测绘学科中出现了“卫星大地测量”的分支。此后由美国卫星建立的全球定位系统(GPS——Global Positioning System)技术在测绘科学中得到广泛应用,建立了利用卫星无线电导航原理的全球定位系统,同时,卫星遥感(RS——Remote Sensing)技术在测绘科学中的应用,可以获得丰富的地面信息,为自动化制图提供了大面积的、全球性的资料。随着现代科学技术的发展,测绘科学也必然会向更高层次的电子化和自动化方向发展。
1.3 地面点位的确定
1.3.1 地球的形状和大小
测量工作是在地球表面的较大范围内进行的,地球的形状和大小直接与测量工作有关。
地球的自然表面有高山、丘陵、盆地、平原、海洋等起伏形态,是一个不规则的曲面。就整个地球表面积而言,海洋面积约占71%,陆地面积约占29%。
假设某一个静止不动的水面延伸而穿过陆地,包围整个地球,形成一个闭合曲面,称为水准面。水准面是作为流体的水受地球重力影响而形成的重力等势面,它的特点是面上任意一点的铅垂线都垂直于该点曲面的切面。
水面可高可低,符合这个特点的水准面有无数个,其中与平均海水面相吻合的水准面称为大地水准面。大地水准面所包围的形体,可以近似地代表地球的形体,称之为大地体。
由于地球自转产生的离心力,使地球形体在赤道处较为突出,在两极处较为扁平,如图1-1所示,其中,PP1为地球自转轴。
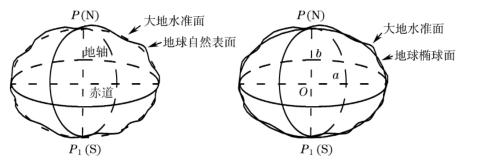
图1-1 地球自然表面、大地水准面和地球椭球面
地球内部质量分布不均匀,重力受其影响,致使大地水准面成为一个不规则的、复杂的曲面。如果将地球表面的点位图形投影到这样一个不完全均匀变化的曲面上,将无法进行计算和绘图。为解决这个问题,可选用一个非常接近大地水准面,并可用数学公式表示的几何形体来建立一个投影面,作为测量上计算、绘图的基准面。
这个数学形体是以地球自转轴PP1为短轴的椭圆PFP1Q绕PP1旋转而成的椭球体,如图1-2所示。其表面称为旋转椭球面,它与大地水准面虽不能完全重合,但是最为接近。
决定地球椭球体形状大小的参数为椭圆的长半径a和短半径b,由此可以计算出另一个参数——扁率α:
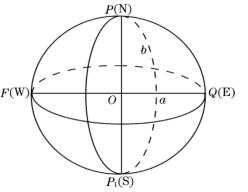
图1-2 地球椭球体
![]()
我国目前采用的参考椭球体是1975年国际大地测量与地球物理联合会推荐的IUGG -75参数:a=6 378 140 m,α=1/298.257,b=6 356 755.288 m。
由于地球的扁率很小,因此当测区范围不大时,可以近似地把地球视为圆球,其平均半径R为6 371 km。
1.3.2 确定地面点位的方法
测量工作的根本任务是确定地面点位。要确定某地面点的空间位置,就是将地面点沿铅垂线投影到某基准面上,求出相对于基准面和基准线的三维坐标或二维坐标。下面介绍几种用以确定地面点位的坐标系。
1)地理坐标系
地理坐标系属球面坐标系,根据不同的投影面,又分为天文地理坐标系和大地地理坐标系。
(1)天文地理坐标系
天文地理坐标又称天文坐标,用天文经度λ和天文纬度φ来表示地面P点投影在大地水准面上的位置,如图1-3所示。自首子午线向东0°~180°称为东经,向西0°~180°称为西经;自赤道起向南0°~90°称为南纬,向北0°~90°称为北纬。
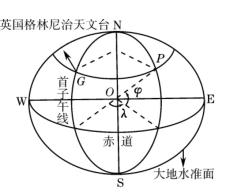
图1-3 地理坐标系
(2)大地地理坐标系
大地地理坐标系用大地经度L和大地纬度B表示地面点投影在地球椭球面上的位置。
确定球面坐标(L,B)所依据的基本线为椭球球面的法线,基本面为包含法线及南北极的大地子午面。
2)地心坐标系
地心坐标系属空间三维直角坐标系,用于卫星大地测量。由于人造地球卫星围绕地球运动,地心坐标系取地球质心(地球的质量中心)为坐标系原点,X、Y轴在地球赤道平面内,首子午面与赤道平面的交线为X轴,Z轴与地球自转轴相重合,如图1-4所示。地面点P的空间位置用三维直角坐标(xp,yp,zp)表示。
3)平面直角坐标系
地理坐标系或地心坐标系是球面坐标,而工程建设的规划、设计和施工均在平面上进行绘图和计算,因此,球面坐标的使用非常不方便。测量的计算、绘图和工程建设的规划、设计和施工一样,最好是在平面上进行。但是地球表面是一个不可展平的曲面,把球面上的点位换算到平面上,称为地图投影。我国普遍采用高斯(Gauss)投影的方法。
(1)高斯平面直角坐标系
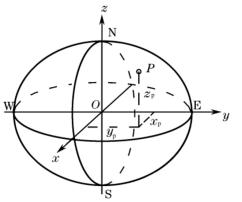
图1-4 地心坐标系
高斯投影的方法首先是将地球按经线划分成带,称为投影带。投影带是从首子午线起,每隔经度6°划为一带(称为6°带),如图1-5所示,自西向东将整个地球划分为60个带。带号从首子午线开始,用阿拉伯数字表示,位于各带中央的子午线称为该带的中央子午线(或称为主子午线),如图1-6所示,第一个6°带的中央子午线的经度为3°,任意一个带中央子午线经度λ0可按下式计算:
![]()
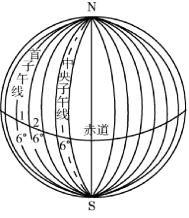
图1-5 高斯投影带
式中:N——投影带号。
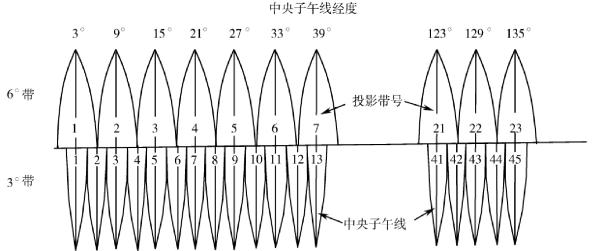
图1-6 6°带和3°带中央子午线及带号
高斯投影中,虽然能使球面图形的角度和平面图形的角度保持不变,但任意两点间的长度却产生变形(投影在平面上的长度大于球面长度),称为投影长度变形。离中央子午线愈远,则变形愈大。变形过大,对于测图和用图都是不方便的。6°带投影后,其边缘部分的变形能满足1∶25 000或更小比例尺测图的精度。当进行1∶10 000或更大比例尺测图时,要求投影变形更小,可采用3°分带投影法或1.5°分带投影法。3°分带从东经1.5°开始,自西向东每隔3°划分一个投影带,将整个地球划分为120个带,如图1-6所示,每带中央子午线的经度λ′0按下式计算:
![]()
式中:n——投影带号。
采用高斯投影时,设想取一个空心圆柱体与地球椭球体相切于某一投影带的中央子午线,如图1-7所示。在球面图形与柱面图形保持等角的条件下,将球面图形投影在圆柱面上;然后将柱体沿着通过南、北极的母线切开,并展开成平面。在这个平面上,中央子午线与赤道成为相互垂直的直线,分别作为高斯平面直角坐标系的纵轴(X轴)和横轴(Y轴),两轴的交点作为坐标的原点,如图1-8(a)所示。
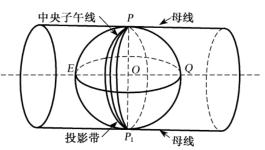
图1-7 高斯平面直角坐标系的建立
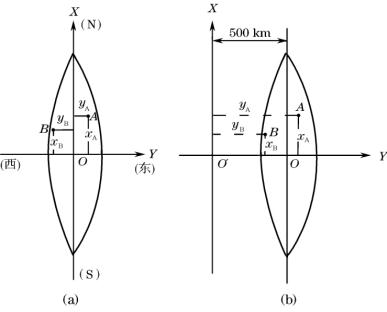
图1-8 高斯平面直角坐标系
在坐标系内,规定X轴向北为正,Y轴向东为正。我国位于北半球,X坐标值均为正,Y坐标值则有正有负。例如,图1-8(a)中,yA=+37 585m,yB=-36 262m。为避免出现负值,将每个投影带的坐标原点向西移500km,则投影带中任一点的横坐标也均为正值。例如,图1-8(b)中,yA=500 000+37 585=537 585m,yB=500 000-36 262=463 738m。
为了能确定某点在哪一个6°带内,在横坐标值前冠以带的编号。例如,设A点位于第19带内,则其横坐标值yA=19 537 585 m。
(2)独立平面直角坐标系
当测量区域较小时,可以把该区域的地球表面当作平面看待,并在该面上建立独立平面直角坐标系,如图1-9(a)所示。将坐标原点选在测区西南角使坐标均为正值,坐标系原点可以是假定坐标值。
独立平面直角坐标系的坐标轴方向和象限编号顺序与高斯平面直角坐标系相同,如图1-9(b)所示。
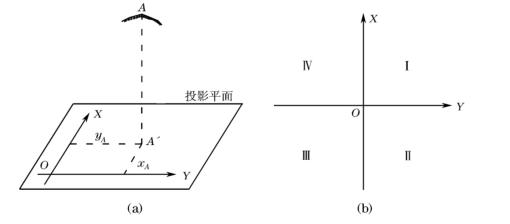
图1-9 独立平面直角坐标系
4)地面点的高程
地面点位置的高低,是用地面点的高程来描述的。由于地面点投影的基准面不同,因此描述地面点高程有绝对高程和相对高程两种。
我国在青岛设立了潮汐站,长期观测和记录黄海海水面的高低变化,取其平均值作为我国的大地水准面位置(其高程为零),并在青岛建立了水准原点。目前,我国采用的是“1985年国家高程基准”,青岛水准原点的高程为72.260 m,全国各地的高程都以它为基准进行测算。但在1987年以前我国使用的是“1956年黄海高程系”,其青岛水准原点的高程为72.289 m。
(1)绝对高程
绝对高程是以大地水准面为基准面的。地面点到大地水准面的铅垂距离称为绝对高程(简称高程,又称为海拔)。图1-10中A、B两点的绝对高程分别为HA、HB。
在大地水准面上,绝对高程为零。
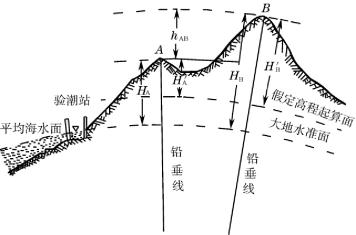
图1-10 高程和高差
(2)相对高程
在局部地区,有时采用绝对高程有困难或不方便时,可假定一个高程起算面(水准面),地面点到该水准面的垂直距离称为相对高程或假定高程。如图1-10所示,H′A、H′B分别表示A点和B点的相对高程。
(3)高差
地面上两点间绝对高程或相对高程之差称为高差,用h表示。如图1-10所示,A、B两点间的高差为
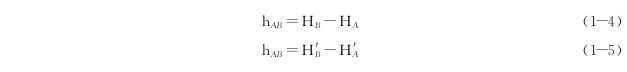
1.4 水平面代替水准面的限度
地球表面是一个弯曲的球面,但其半径很大,如果测量区域较小,可以用一个水平面代替水准面。下面通过讨论用水平面代替水准面后对距离和高程的影响,给出水平面代替水准面的限度。
1.4.1 对距离的影响
设大地水准面P与水平面P′在A点相切,如图1-11所示。A、B两点在大地水准面上的距离为D(弧长),在水平面上的距离为D′(切线长),球面半径为R,D所对的圆心角为θ,则以水平面上的距离D′代替球面上弧长D所产生的误差为ΔD,则
![]()
将tanθ按级数展开,得
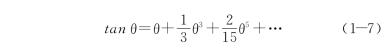
因θ值很小,取至第二项,代入式(1-6),得
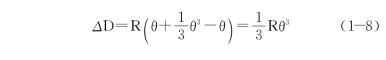
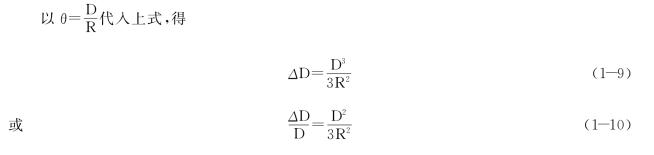
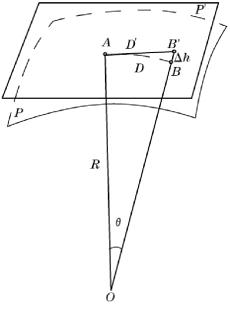
若取地球的半径R=6 371 km,并以不同的D值代入式(1-9)或式(1-10),则可得距离误差ΔD和相对误差ΔD/D,如表1-1所示。
表1-1 水平面代替水准面的距离误差和相对误差
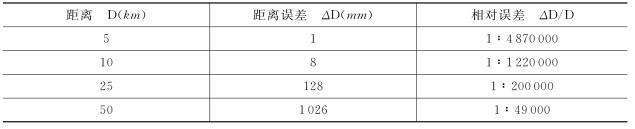
由表1-1可见,用切线长D′代替弧长D,在距离不到10 km时产生的最大误差约为1 cm,这样的误差即使在地球表面上作精密的水平距离测量时也认为是可以允许的。所以,在半径为10 km的小区域内,地球曲率对于水平距离的影响可以忽略不计。在精度要求较低的测量中,则测量范围的半径可扩大到25 km。
1.4.2 对高程的影响
如图1-11中,由于A、B两点位于同一水准面上,所以其高程相等。B点在水平面上的投影为B′点,则BB′即为水平面代替水准面所产生的高程误差。设BB′=Δh,则
![]()
整理后得
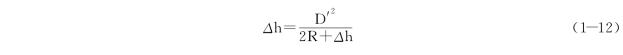
由于D′与D相差很小,可以用D代替D′,同时Δh与2R相比可以忽略不计,则
![]()
同样,以不同的D值代入式(1-13)中,取R=6 371 km,可以得相应的高程误差,如表1-2所示。
表1-2 水平面代替水准面的高程误差

由表1-2可知,用水平面代替水准面,在1 km的距离上高程误差为78 mm。因此,在水准测量时,即使很短的距离也应考虑地球曲率的影响,采用相应的措施减小误差。
1.5 测量工作概述
1.5.1 测量工作的基本原则
地球表面的外形是复杂多样的,在测量工作中,一般将其分为两大类:地面上自然形成的高低起伏变化,例如山岭、溪谷、平原、河海等称为地貌;地面上由人工建造的固定附着物,例如房屋、道路、桥梁、界址等称为地物。地物和地貌统称为地形。测量任务之一就是要把这些地物和地貌缩小表示在图纸上,这张图称为地形图。
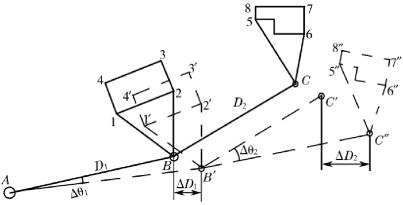
图1-12 测站误差积累对测图的影响
例如测绘一个地区的地形图,要在地面的某些点上安置测绘仪器(这些点称为测站),测定地形特征点,缩绘成图。如果一开始就从测区内的第一点A起连续进行测量,如图1-12所示,即在测完A站附近地形之后,测定第二点B的位置,然后搬到B站测绘地形,继而测定C点位置,又在C站继续测绘,如此直至测完全测区。采取这种方法由于测定每一测站均有误差存在,且前一站的误差将传递给后一站,误差逐站积累。如图中测定B点时有误差Δθ1及ΔD1,使它的平面位置移至B′;测C点时,由于前站B的误差,C点的位置移至C′;又因测定C点时的误差Δθ2与ΔD2,致使它的位置最后移至C″。假定测量房屋中没有误差,由此所测得的房屋将从正确位置5、6、7、8移至5″、6″、7″、8″。如测站越多,误差积累越大,不可能得到一张合乎精度要求的地形图,因此不能采用这种方法进行测量。
为了防止误差积累和传播,保证测区内点位之间具有规定的精度,在实际测量工作中应遵循“布局上‘由整体到局部’,次序上‘先控制后碎部’,精度上‘从高级到低级’”的基本原则。
1.5.2 测量工作的基本内容
根据测量次序上遵循“先控制后碎部”的原则,先要进行控制测量,然后再进行碎部测量。
1)控制测量
控制测量分为平面控制测量和高程控制测量。控制测量首先在测区范围内选定若干控制点作为骨干,组成控制网,如图1-13中选择A、B、C、D、E、F等点,组成一个闭合多边形。先进行比较精确的距离、水平角和高程等测量,然后按照控制网图形的几何条件,进行某些必要的计算,精确地求出这些控制点的平面位置和高程,并将点位展绘在图上,最后再以这些控制点作为测站来测绘地形。前者测定控制点位置的工作称为控制测量,后者测绘地形的工作称为碎部测量。由于控制点的位置比较准确,在每个控制点上测绘地形的误差只影响局部,不致影响整个测区。
2)碎部测量
在控制测量的基础上,再进行碎部测量。碎部测量是以控制点为依据,以较低的精度(保证必要的精度)由控制点测定碎部点(地形特征点)的位置,如图1-14所示。例如,在控制点A附近房屋角点1、2、3,当测定一定数量的碎部点位置后,可按一定比例尺将这些碎部点标绘在纸上,绘制成图。
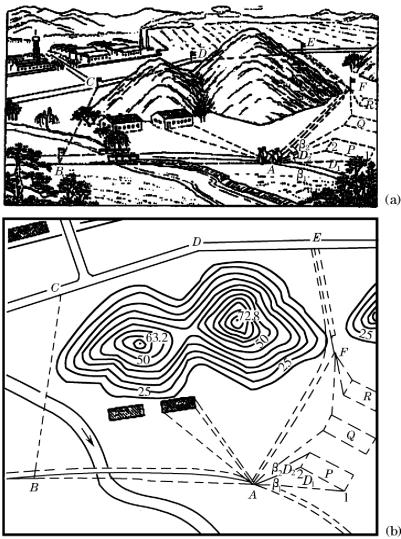
图1-13 控制测量和细部测量示意图
在地面有高低起伏的地方,根据控制点,可以测定一系列地形特征点的平面位置和高程,据此绘制用等高线表示的地貌,如图1-15所示,注于线上的数字为地面的高程。
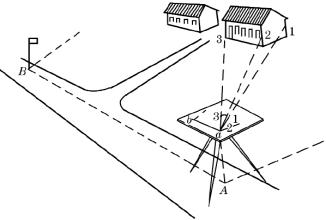
图1-14 地物的细部测绘
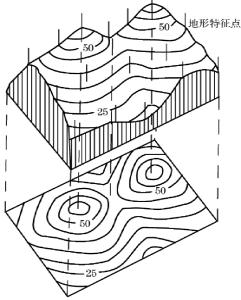
图1-15 用等高线表示地貌
3)测量的基本工作
综上所述,控制测量和碎部测量的基本任务都是为了确定点的空间位置,所进行的基本工作都是量距、测角、测高差。因此,距离、角度和高差这三个确定地面点位的量称为基本观测量。
测量工作分为内业和外业。在野外利用测量仪器和工具测定地面上两点的距离、角度和高差,称为测量的外业工作;在室内将外业的测量成果进行数据处理、计算和绘图,称为测量的内业工作。
1.6 测量常用计量单位及其换算
测量工作中,常用的长度、面积、体积和角度的计量单位的名称、符号及单位换算,必须依据的是《中华人民共和国法定计量单位》(1984年2月27日国务院公布)。
1.6.1 测量长度单位及其换算
我国测量工作的法定长度计量单位为米(m)制单位,具体换算如下:
1 m(米)=10 dm(分米)=100 cm(厘米)=1 000 mm(毫米)1 hm(百米)=100 m
1 km(千米或公里)=1 000 m
在测量工作过程中,还会用到英制的长度计量单位,它与米制长度单位的换算关系如下:
1 in(英寸)=2.54 cm
1 ft(英尺)=12 in=0.304 8 m 1 yd(英码)=3 ft=0.914 4 m 1 mi(英里)=1 760 yd=1.609 3 km
1.6.2 测量面积单位及其换算
我国测量工作的法定面积单位为平方米(m2),大面积采用公顷(hm2),平方公里或平方千米(km2);我国农业土地常用亩(mu2)为面积计量单位,它们的换算关系如下:
1 m2(平方米)=100 dm2=10 000 cm2=1 000 000 mm2 1 mu(亩)=10分=100厘=666.666 7 m2 1 are(公亩)=100 m2=0.15 mu 1 hm2(公顷)=10 000 m2=15 mu
1 km2(平方千米)=100 hm2=1 500 mu
美制与英制面积单位的换算关系如下:
1 in2(平方英寸)=6.451 6 cm2
1 ft2(平方英尺)=144 in2=0.092 9 m2
1 yd2(平方码)=9 ft2=0.836 1 m2
1 acre(英亩)=4 840 yd2=40.467 2 are=6.07 mu
1 mi2(平方英里)=640 acre=2.59 km2
1.6.3 测量体积单位
我国测量工作的法定体积单位为立方米(m3)。1 m3(立方米)也可称为1立方或1方。
1.6.4 测量角度单位及其换算
我国测量工作的法定角度计量单位有60进制的度、分、秒制和弧度制,具体换算关系如下:
1)度分秒制
1圆周=360°(度),1°(度)=60′(分),1′=60″(秒)
2)弧度制
![]()
式中,取π=3.141 592 654。
1弧度(rad)对于度分秒制的角度值为

角度单位的度、分、秒值,可按下式化为弧度值
![]()
本章小结
测量学是一门研究地球的形状和大小以及确定地面(包含空中、地下和海底)点位的学科。它的内容包括测定和测设两个部分。
测量工作的根本任务是确定地面点位。为了确定地点的位置,首先要建立确定地点位置的基准。
假设某一个静止不动的水面延伸而穿过陆地,包围整个地球,形成一个闭合曲面,称为水准面。水准面是作为流体的水受地球重力影响而形成的重力等势面,它的特点是面上任意一点的铅垂线都垂直于曲面在该点的切面。
水面可高可低,符合这个特点的水准面有无数个,其中与平均海平面相吻合的水准面称为大地水准面。大地水准面所包围的形体,可以近似地代表地球的形体,称为大地体。
确定地面点位的坐标系有:天文地理坐标系、大地地理坐标系、地心坐标系、高斯平面直角坐标系、独立平面直角坐标系。
地面点位置的高低,是用地面点的高程来描述的。由于地面点投影的基准面不同,因此描述地面点高程有绝对高程和相对高程两种。
地面点到大地水准面的铅垂距离称为绝对高程。地面点到假定水准面的垂直距离称为相对高程或假定高程。地面上两点间绝对高程或相对高程之差称为高差。
地球表面是一个弯曲的球面,但其半径很大,如果测量区域较小,可以用一个水平面代替水准面。
测量工作中应遵循“布局上‘由整体到局部’,次序上‘先控制后碎部’,精度上‘从高级到低级’”的基本原则。
根据测量次序上遵循“先控制后碎部”的原则,先要进行控制测量,然后再进行碎部测量。控制测量分为平面控制测量和高程控制测量。选取一系列控制点构成控制网,进行控制测量。碎部测量是以控制点为依据,以较低的精度(保证必要的精度)由控制点测定碎部点(地形特征点)的位置。
距离、角度和高差这三个确定地面点位的量称为基本观测量。
测量工作分为内业和外业。在野外利用测量仪器和工具测定地面上两点的距离、角度和高差,称为测量的外业工作;在室内将外业的测量成果进行数据处理、计算和绘图,称为测量的内业工作。
习题与思考题
1.测量学研究的对象是什么?
2.测量学的任务是什么?测定与测设有何区别?
3.测量学在工程建设中有什么作用?
4.何谓水准面?何谓大地水准面?何谓大地体?
5.确定地面点位常采用哪几种坐标系?
6.高斯平面直角坐标系是怎样建立的?
7.测量上的平面直角坐标系和数学上的平面直角坐标系有何区别?
8.已知某点的高斯平面直角坐标为x=3 102 467.28 m,y=20 592 538.69 m,试问该点位于6°带的第几带?该带的中央子午线经度是多少?该点在中央子午线的哪一侧?在高斯投影面上,该点距中央子午线和赤道的距离约为多少?
9.何谓绝对高程?何谓相对高程?何谓高差?
10.用水平面代替水准面时,地球的曲率对距离、高差有何影响?
11.测量工作的基本原则是什么?为什么要遵循这些基本原则?
12.确定地面点位的三项基本工作是什么?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















