双因子方差分析

第三节　双因子方差分析

双因子方差分析是指同时考察两个因子或因素对试验指标的影响。例如，研究不同内容的广告和不同的销售价格这两个因素对销售额的影响；在超级市场中研究不同货架位置和不同商品色彩对商品销售量的影响；研究不同的耕作深度和不同的施肥量对农作物产量的影响；研究不同的配方与不同的加工温度对产品质量的影响；研究不同的家庭人口和不同收入水平对消费额的影响；养老院价格和位置对养老院入住率的影响等，都是双因子方差分析。

在双因子方差分析中，由于存在两个因子的影响，各因子不同水平的搭配还会产生新的影响，称为交互作用。各因子间是否存在交互作用是多因子方差分析新产生的问题，也是单因子方差分析与多因子方差分析的区别所在。

一、无交互作用的双因子方差分析

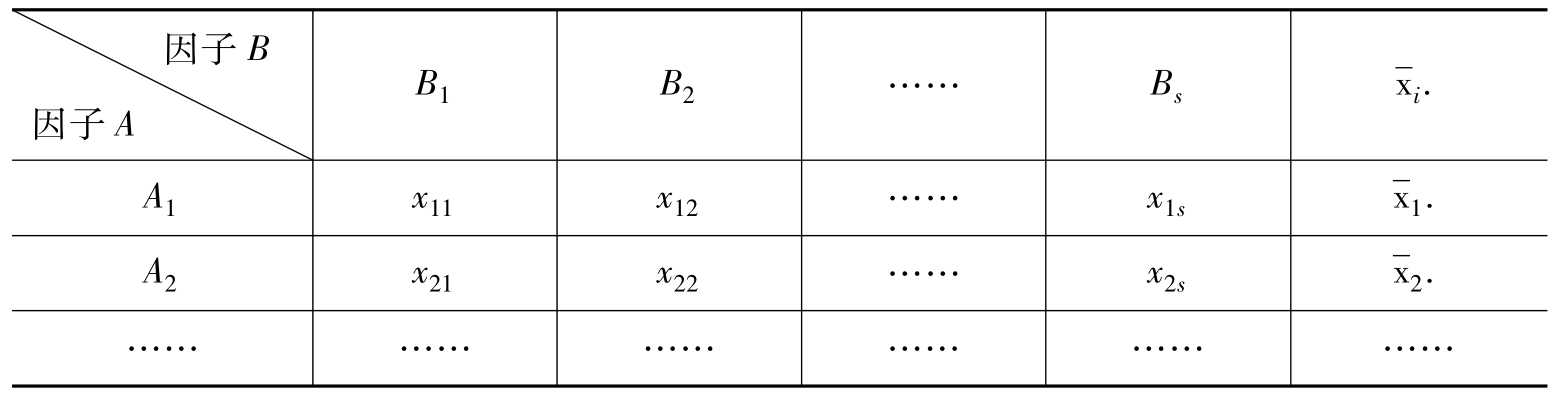
为了更好地了解双因子方差分析，首先考虑没有交互作用的情况。设因子A有γ个不同的水平A₁，A₂，A₃……A_γ；因子B有S个不同的水平B₁，B₂，B₃……B_s。在其他因素都加以控制的条件下，因子A的每一个水平和因子B的每一个水平组成一组试验条件，对每种情况进行一次独立试验，共可得到γ×S个试验结果x_ij，其数据结构见表9.8。

表9.7　　　　　　　　　　无交互作用双因子方差分析表

续上表

其基本假设为:

对因素A:H₀₁:μ₁.=μ₂.=μ₃.……=μ_γ.；H₁₁:μ₁.，μ₂.，μ₃.，……，μ_γ.不全相等

对因素B:H₀₂:μ.₁=μ.₂=μ.₃……=μ._γ；H₁₂:μ.₁，μ.₂，μ.₃，……，μ._γ不全相等

表中μ₁.是数学期望，其余类似:

表9.8　　　　　　　　　　双因子方差分析的数据结构表

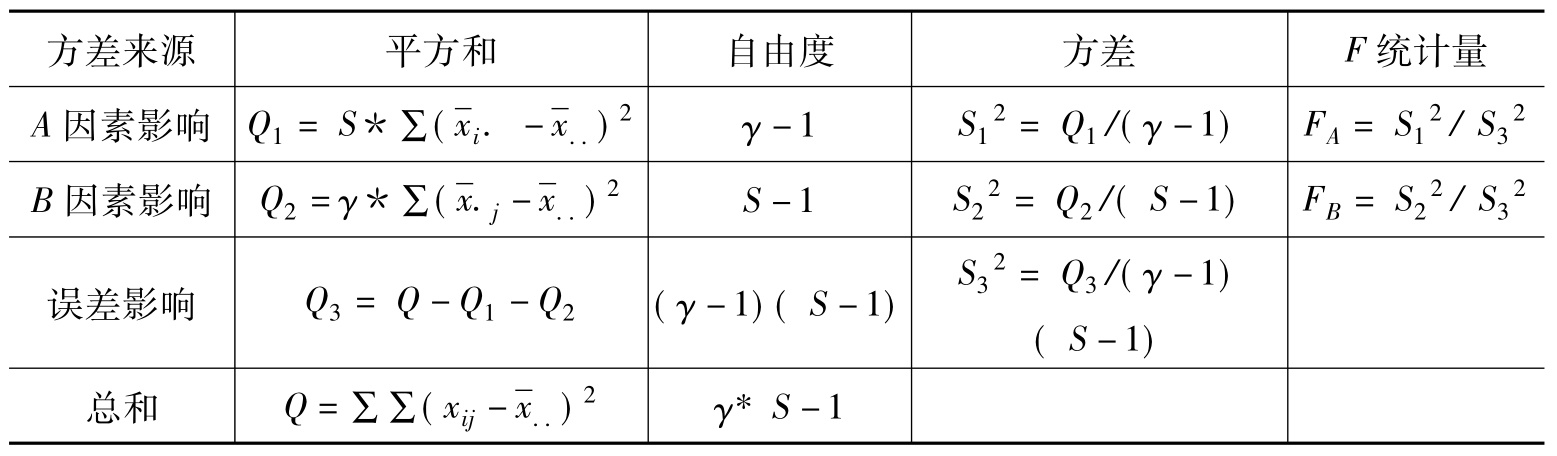
双因子方差分析就是要求公式中四者的平方和，再对它们的方差进行分析。其方差分析表见表9.9。

表9.9　　　　　　　　　　无交互作用双因子方差分析表

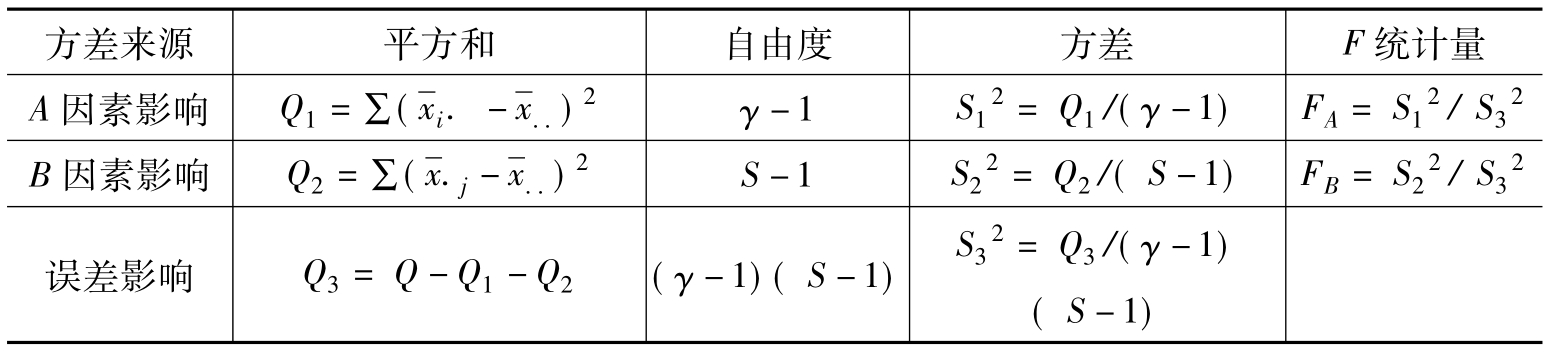
续上表

现以［例9.2］的资料说明无交互作用双因子方差分析。

解:γ=3，S=4，γ*S=12

(1)在表9.2中，12个数据的总平均数及总离差平方和为: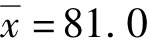

(2)因子A的三种水平的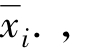分别为89，75，79。则:Q₁=416

(4)方差总和，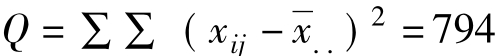

(5)随机误差平方和Q₃=Q－Q₁－Q₂=228

(6)方差分析表见表9.10。

表9.10　　　　　　　　　　方差分析表

(7)计算统计量F_A、F_B

F_A=S₁²/S₃²=4.101；F_B=S₂²/S₃²=0.949

(8)若给定显著水平α=0.05，查表得临界值F_0.05(2，6)=5.14，F_0.05(3，6)=4.76。显然F_A值小于临界值(5.47＞5.14)，而F_B值小于临界值(1.32＜4.76)。因此，我们有95%的把握说不同销售方式对该产品销售量的影响明显，而销售地点对该产品销售量的影响不大。

二、有交互作用(重复观察情况下)的双因子方差分析

交互作用就是不同因子对试验所考察的指标具有复合作用。在实际问题研究中，常常遇到因子A的作用随因子B的水平变化而变化。例如，超市仅考虑不同货架位置和不同商品色彩对商品销售量都无影响，但是既考虑货架位置又考虑不同商品色彩，则对商品销售量就有影响了。再如，水稻亩产量在施加磷、氮肥3千克后，比不施氮肥的情况下，产量可相应增加15千克/亩、20千克/亩；而在施氮肥3千克时同时施加磷肥3千克后，亩产就增加40千克/亩。这表明氮肥和磷肥对水稻亩产量有交互作用，但A、B两因素的综合效应不是两因素效应的简单相加。当需要考虑两个因子的交互作用时，每组试验条件相同的试验至少要做两次，才能将交互作用的平方和从误差平方和中分解出来。

设因子A取γ个水平，因子B取S个水平，共有γS个水平组合A_iB_j，每个水平组合A_iB_j，重复L次试验，每次试验结果的数据用x_ijk表示(k=1，2，…，L)。其数据结构见表9.11。

表9.11　　　　　　　　　　有交互作用双因子方差分析数据表

设因子A的第i个水平的效应: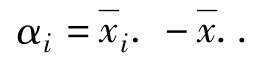

因子B的第j个水平的效应: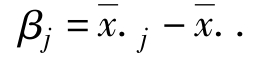

其中: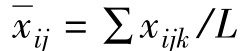

则任意一项试验数据可分解为: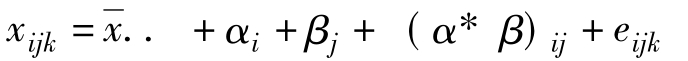

有交互作用的两因子方差分析，就是要先求出上式中五项的平方和，然后计算各自的方差及其统计量F_A、F_B、F_AB，最后检验因子A、因子B以及交互作用三者各自的影响是否显著。其方差分析表见表9.12。

表9.12　　　　　　　　　　有交互作用双因子方差分析表

［例9.4］初婚年龄随文化程度和家庭居住情况而异，文化程度仍分大学以上A₁，高中A₂，初中A₃，小学及其以下等四种，女性家庭居住情况分城市B₁、城镇B₂和农村B₃三种。某社区随机挑选24名已婚女性，分为12组，每组2人，每组每个妇女的初婚年龄记录如表9.1所示。问不同文化程度(A)、不同家庭背景(B)的妇女初婚时间是否有显著的差别。

表9.13　　　　　　　　　　不同文化程度不同家庭背景下的女性初婚年龄

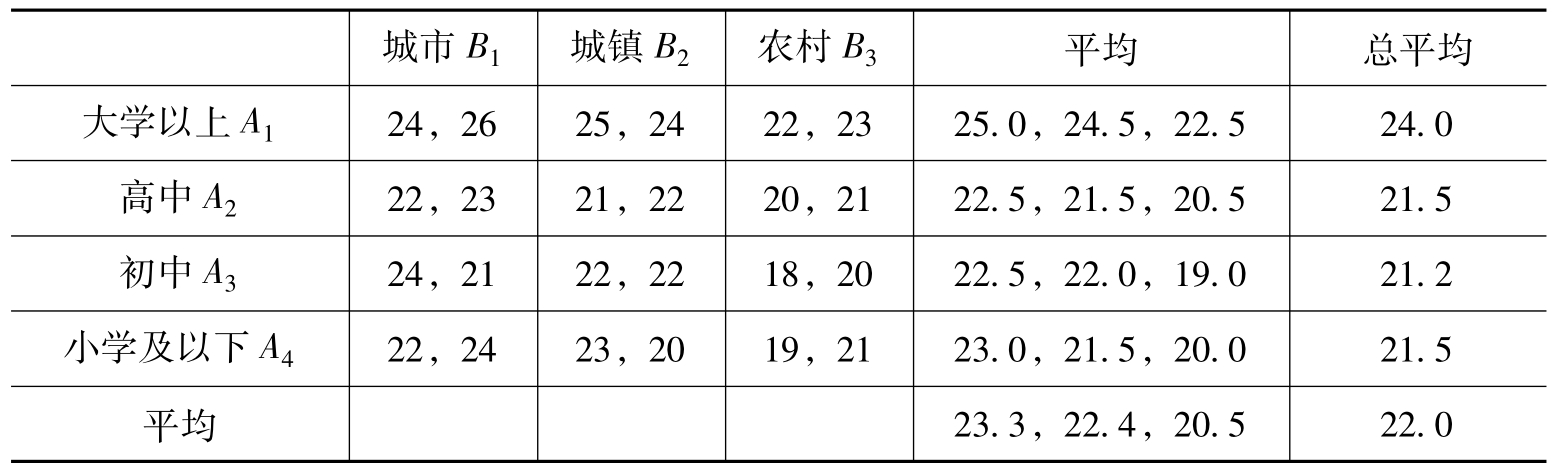
解:显然L=2，γ=4，S=3

(1)表中24个试验数据的总平均数和离差平方和为: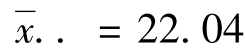Q=84.96

(2)因子A的四种水平的平均数24.0，21.5，21.2和21.5与总平均数22.04的离差平均方和为: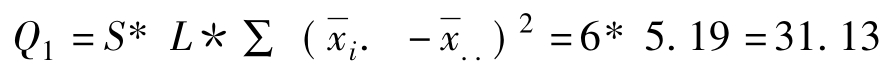

(3)因子B的三种水平的平均数22.3，22.4，29.5与总平均数22.04的离差平均方和为:

(4)表中每组试验做两次，共有12组试验，每组试验均产生一个误差平方和，则误差平方总和为:

(5)因子A*B交互作用产生的离差平方和为:

Q₃=Q－Q₁－Q₂－Q₄=84.96－31.13－31.72－19.50=2.61

(6)根据以上计算，得方差分析表见表9.14。

表9.14　　　　　　　　　　方差分析表

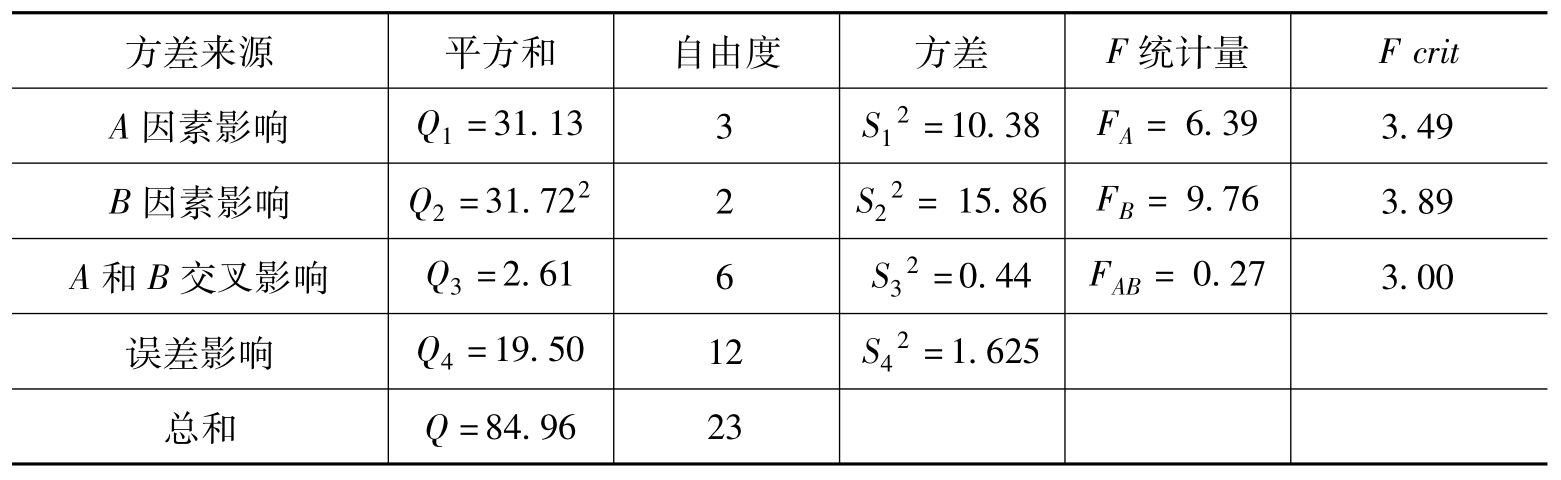
(7)计算F统计量如上表，并作F检验。

若显著水平α=0.05，查表得临界值F_0.05(3，12)=3.49，F_0.05(2，12)= 3.89，F_0.05(6，12)=3.00。由于F_A、F_B的数值均大于临界值，因此，根据试验的数据资料，有95%的把握可以断定文化程度和家庭背景对女性初婚年龄的影响是显著的，文化程度和家庭背景之间不存在明显的交互作用。从资料可见，城市女性和大学以上女性初婚年龄最迟，而农村和初中文化程度结婚较早。