分组的类型

三、分组的类型

资料的分组有不同的类型，不同的分组类型有不同的分组方法。

根据所使用的分组标志的数量，可以将分组分为简单分组和复合分组两类。简单分组是对调查对象只按一个标志进行的分组。例如，家庭规模按家庭人口数分为核心家庭、主干家庭、联合家庭；工业企业按所有制标志分为国有企业、集体所有制企业、私营企业、三资企业等。复合分组是用两个或两个以上的标志对调查对象依次进行的分组。例如，将人口按婚姻状况和性别两个标志进行分组，见表9-5。

表9-5　某市性别、婚姻状况的人口数

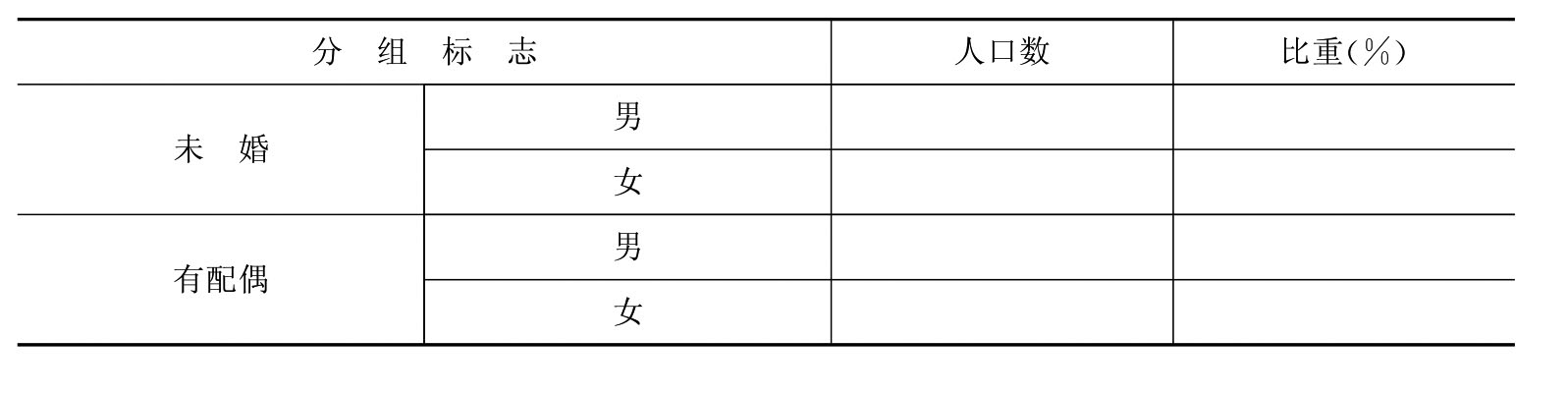
（续表）

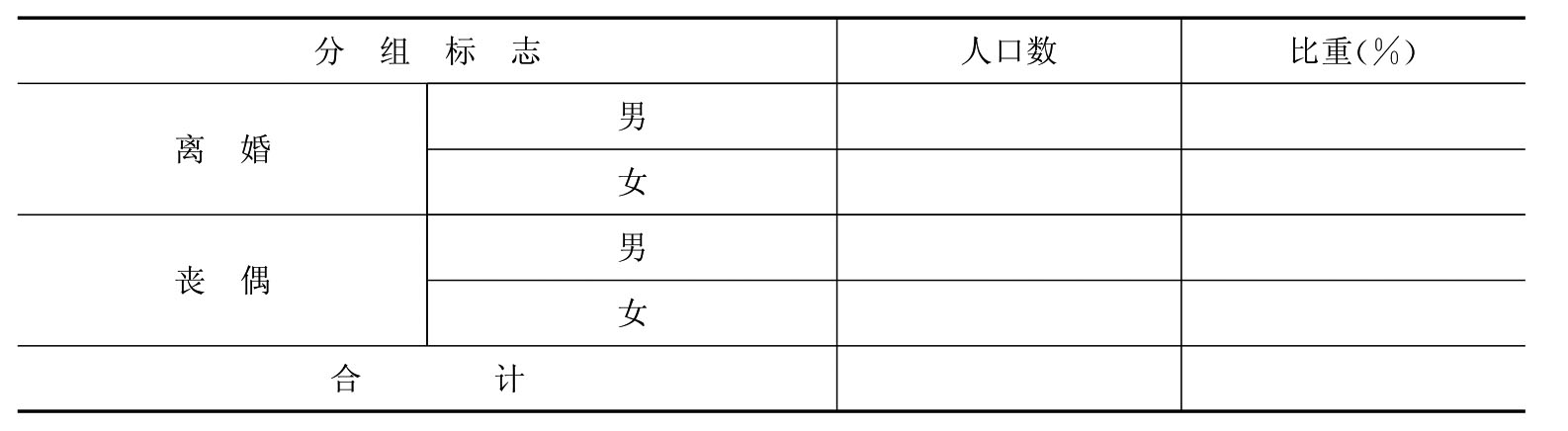
复合分组并不是分组越细越好。因为，每多分一次组，组数都将成倍地增加，而分到各组的单位数却大大减少，这将造成分析的困难。复合分组一般以2至3个标志分组较为适宜。

根据所使用的分组标志的性质的不同，资料分组又可以分为按品质标志分组和按数量标志分组两类。按品质标志分组就是按事物的性质分组。例如，按调查对象的性别、民族、职业等特征进行分组。按品质标志分组，组数的确定比较简单，只要确定了分组标志就知道了它的组数。如按性别标志分组，就可以将调查对象分成男、女两个组。

按数量标志分组就是按事物的数量特征进行分组。例如，按调查对象的年龄、工龄、收入等特征进行分组。根据总体各单位标志值变动范围的大小，按数量标志分组又可以分为两种类型，即单项式分组和组距式分组。

当数量标志值的变动范围较小，而且标志值的项数不多时，可进行单项式分组，即可直接将每个标志值列为一组。如表9-6所示。^[4]

表9-6　2010年按家庭户类别划分的户数分布

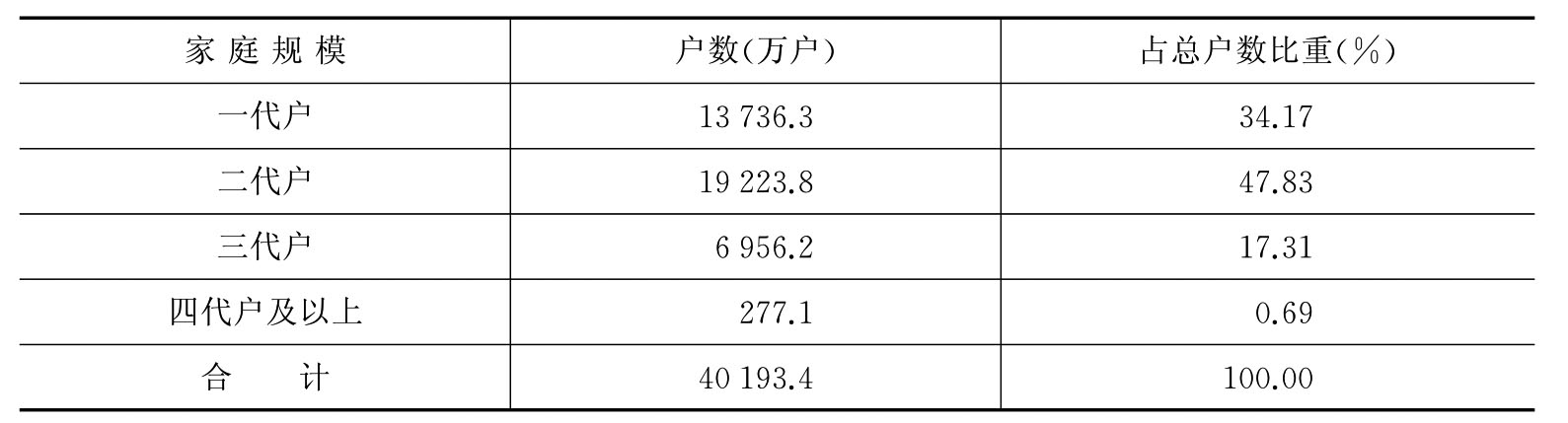
当数量标志值的变动范围较大，标志值的项数又较多时，就可将一些邻近的标志值合并为一组，作为分组的依据，以减少组的数量。这种以标志值的一定变动范围为分组依据的方法叫做组距式分组。例如，某班40名学生的社会调查课考试成绩如下:

89 88 76 99 74 60 82 60 89 97

86 93 99 77 73 98 79 59 78 63

95 70 87 84 79 82 77 67 83 79

72 84 85 56 81 94 65 65 66 92

由于上述标志值（成绩）的变动范围较大，标志值的项数又较多，故可以10分这个变动范围作为分组的依据，如表9-7所示。

表9-7　某班40名学生社会调查课考试成绩统计表

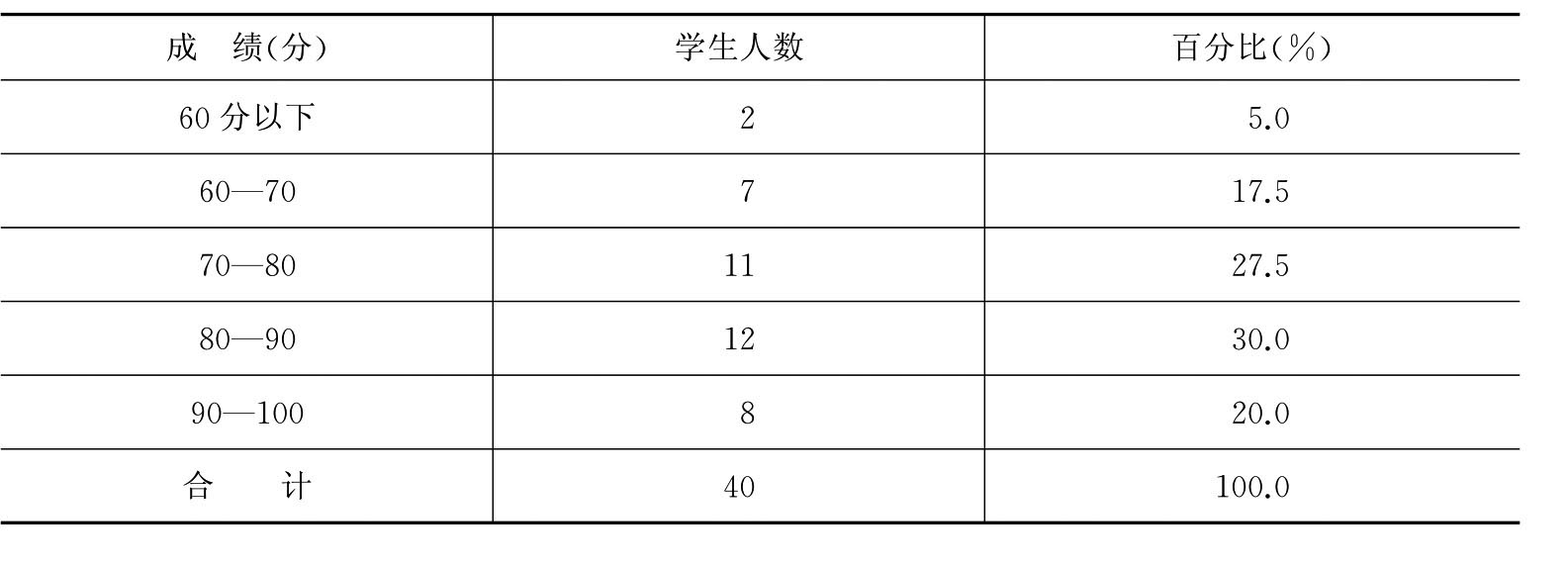
组距式分组的组数的确定，应从调查研究的实际需要出发。组数太少，会失去分组的意义；组数太多，又会给统计分析带来困难。根据经验，组数一般以5至8组为宜。

组距，是指各组中最大数值与最小数值之间的差距。组距与组数有密切的关系，在标志值的变动范围一定的情况下，组距越小，组数越多；组距越大，组数就越少。在确定组距与组数的具体操作中，一般是先大体确定组距（通常采用5、10、100等整数作为组距），再用全部标志值中最大数值与最小数值之间的差距，即全距除以组距，就可得出组数。如果算出的组数太多或太少，再可将组距作适当调整。

在组距式分组中，各组组距有相等的，也有不相等的。在实际的调查研究中，大多数情况下是按等距分组，但也有将调查资料按不等距分组的。如国家统计局1986年对农民的人均纯收入按贫困、温饱、小康、富裕四种类型进行划分时，组距是这样规定的:200元以下为贫困户，200元至500元为温饱户，500元至1 000元为小康户，1 000元以上为富裕户。这是一种组距不相等的划分方法，这种划分法比等距划分法能更好地反映出调查对象的实际情况。

组距的两端数值为分组界限。各组的起点数值（最小数值）称为下限，终点数值（最大数值）称为上限。上限与下限的差距即为组距。

组距的表现形式有两种，一种是封闭式的，一种是开口式的。封闭式组距是指上限与下限都确定的组距，开口式组距是指只有上限或只有下限的组距，详见表9-8。

表9-8　某乡农民家庭人均纯收入分组表

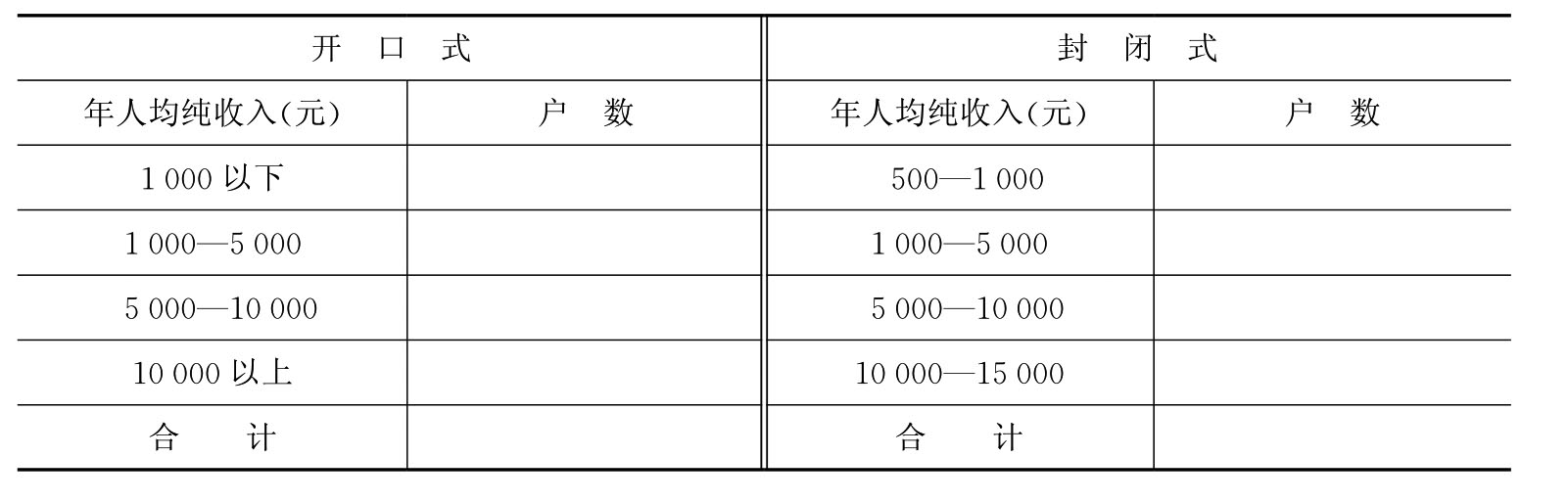
如表所示，我国的社会调查或统计教科书上所用的分组界限通常都是标明界限，而不是真实界限。标明界限的低数组的上限即为高数组的下限。当某一标志值正好与这一分组界限重合时，一般都遵循“上限不在内”的原则，将其划归属于下限的那一组，如表9-11中，某一农民家庭的人均纯收入正好是5 000元，就应划归5 000元至10 000元这一组内。

组中值，是上限与下限之间的中点数值。其计算公式为:

封闭式组距:

开口式组距:

①表9-11中缺下限的组中值的计算方法:按公式计算出的结果小于该组上限的一半，就用该组上限的一半为组中值；按公式计算出的结果大于该组上限的一半，则该结果就是组中值。表9-11中，算出的结果是－1 000，小于500，则组中值是500。如果相邻组是1 000—1 500，算出的结果是1 000－（1 500－1 000）/2＝1 000－250＝750，则750就是组中值。