【摘要】:10.3.1 空间投影融合算法空间投影算法的基本表达式如下:其中:SD为空间细节;c为权重因子,根据实际需要,可以调整该因子的值,用以在空间分辨率和光谱分辨率之间达到平衡。由于高斯尺度空间中每一层的影像都是由高斯卷积核与上一层影像卷积而成,根据高斯函数的性质,可以用一个新的高斯核函数代替这个连续卷积过程,新的高斯核函数的方差的平方是所有连续卷积核函数方差的平方和。图10-10 基于空间投影融合算法的结果
空间投影融合算法_城市遥感
10.3.1 空间投影融合算法
空间投影算法的基本表达式如下:
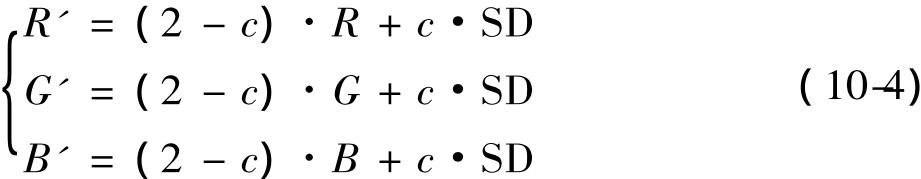
其中:SD为空间细节(spatial details);c为权重因子,根据实际需要,可以调整该因子的值,用以在空间分辨率和光谱分辨率之间达到平衡。
假设高斯尺度空间有s层,尺度因子从σ变化到2σ,层与层之间的尺度因子倍增关系为k=21/s,则对于某一个尺度因子σp=kσ,第p层影像可以描述为:
Ip=G(x,y;σp)·Ip-1 (10-5)
由此可以定义此层影像的空间细节特征为:
hp=Ip-1-Ip (10-6)
若高斯尺度空间有s层,则全色影像的空间细节特征定义为:
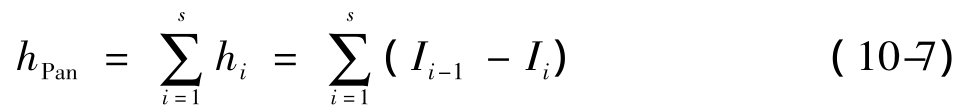
同理,此亮度影像的空间细节特征定义为:
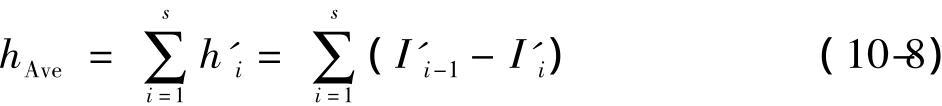
因此,SD按下式计算:
SD=hPan-hAve (10-9)
以上是常规的空间投影算法。由于高斯尺度空间中每一层的影像都是由高斯卷积核与上一层影像卷积而成,根据高斯函数的性质,可以用一个新的高斯核函数代替这个连续卷积过程,新的高斯核函数的方差的平方是所有连续卷积核函数方差的平方和。于是可以得到下面的快速空间投影算法:
SD=Pan-G(x,y;σ')*Pan-(Ave-G(x,y;σ')*Ave)
(10-10)
空间投影和快速空间投影算法对图10-1的影像进行融合后的效果如图10-10所示。

图10-10 基于空间投影融合算法的结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















