球面天文学的建立

无论是预测新月的出现、还是确定祷告的时刻和清真寺的朝向，对这些问题的解决，在数学上都依赖于球面三角学的发展。而球面三角学这一个数学分支的发展，正是伊斯兰天文学家们做出的贡献。

当初托勒密在解决一些天文问题时，虽然也需要根据天球上球面三角形已知的边或角来求解未知的边和角，但他运用较为笨拙的弦函数。到公元9世纪，三角学中的六个函数已经被发现。正弦函数从印度被介绍给了伊斯兰，一同被介绍进来的还有在计算影长时非常重要的正切和余切函数。

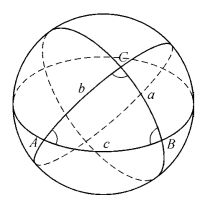
图5.3　球面三角形的边和角

大约在830年，在巴格达的波斯天文学家、数学家哈西卜（Ahmad ibn'Abdallah Habash al－Hasib al－Marwazi，死于864到874年之间）编造了步长为15′的正弦表，并且还编制了间隔为1°的正切表。如前文所提及的，后来阿布·瓦法进一步编制出了步长间隔为15′的正弦表和正、余切表，特别是比鲁尼还利用二次内插法编制了正弦、正切函数表。

是阿尔巴塔尼把三角学加以系统化。他提出了正弦、余弦、正切、余切等三角学术语；正割、余割这两个术语则是阿布·瓦法最早引入的。阿尔巴塔尼发现了其中几个基本的三角函数关系式，他还发现了球面三角形的余弦定理（A、B、C为球面三角形的三个角，a、b、c为对应的边）：

cos a＝cos bcos c＋sin bsinccos A

阿布·瓦法和比鲁尼等人进一步丰富了三角学公式。阿布·瓦法证明了平面和球面三角形的正弦定理。比鲁尼则证明了正弦公式、和差化积公式、倍角公式和半角公式。这些伊斯兰天文学家发现的三角学基本恒等式，大大简化了天球上球面三角形所涉及的计算。

到了马拉盖天文台的纳西尔丁·图西那里，平面和球面的三角学已经成熟到开始脱离天文学成为一门独立的数学分支。他所著的《论完全四边形》（Treatise on the Quadrilateral）是一本纯粹的三角学专著。该书系统阐述了平面三角学，明确给出了正弦定理，讨论了球面完全四边形，对球面三角形进行了分类，特别是首次给出了球面直角三角形的6种边角关系。设球面三角形ABC中，a、b、c分别为角A、B、C的对边，A为直角，则：

cos a＝cos bcos c

cos a＝cot bcot c

sin b＝sin asin B

cos C＝cot atan b

cos B＝sin Ccos b

sinc＝tan bcot B

这些定理和公式，正是现在球面天文学的基本内容。在纳西尔丁·图西的书中，三角学基本上已经达到了现代形态。