太阳和月球的重量

奇怪的是，太阳虽然相距遥远，但是它的重量却比离我们较近的月亮更容易求出来（当然，这里的“重量”，是指质量而言。）

我们使用以下论证方法来计算太阳的质量。实验证明，1克的物体对于相距1厘米的另一个物体的引力等于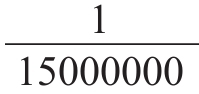毫克[4]。两个质量分别为M和m的物体，相距D时，根据万有引力定理，彼此之间的引力f是：

如果太阳的质量M用克表示，m是地球的质量，D是太阳和地球之间的距离，等于150000000千米，那么，它们之间的相互引力等于：

此外，这个引力就是把地球维持在轨道上的那个向心力。在力学中它等于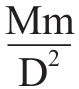，此处的单位是毫克。这里的m是地球的质量（克），v是地球的公转速度，等于30千米/秒，或者3000000厘米/秒，D是地球到太阳的距离。由此可得：

从这个方程式可以求出未知数M（克）：

M=2×1033克=2×1027吨。

用这个数字除以地球的质量：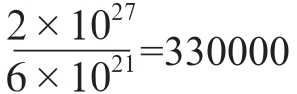

还有一种运用开普勒第三定律求太阳质量的方法。把这一定律和万有引力原理结合在一起，得到一个公式：

这里的Ms是太阳的质量，T是行星绕日的恒星周期[5]，a是行星到太阳的平均距离，m是行星的质量。将这个法则运用到地球和月亮，可以得到：

带入各个已知的数据，因为我们要求的是近似值，所以可以把分子中地球的质量略去，因为它和太阳的质量比较起来太小了，分母中的月球质量也可以省去，这样就得到：

知道了地球的质量，就可以求出太阳的质量了。

这样就可以知道太阳的重量是地球的330000倍。

太阳的平均密度也很容易能求出来：只需要用太阳的体积去除太阳质量就可以。算出的结果显示，太阳的密度是地球的。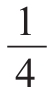

至于月球的质量，就像一位天文学家说的：“它的距离虽然比别的天体都近，但是称出它的重量却比称出（当时）最远的海王星还难。”月亮没有卫星。科学家采取了一些更为复杂的方法来求月球的重量。这里介绍一种：将太阳引起的潮汐和月亮引起的潮汐的高度进行比较。

潮汐的高度与引起它的天体质量和距离有关。太阳的质量和距离已知，月球的距离也是知道的，所以比较潮汐的高度就可以帮助我们算出月球的质量。我们稍后讲潮汐的时候会讲到这个问题。再次给出一个最终结论：月球的质量是地球的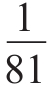（图91）。

图91　地球的重量是月球的81倍。

既然月球的半径是知道的，那么就可以求出它的体积了。它的体积是地球的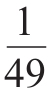。所以，月球的平均密度和地球的平均密度之比是：

这就是说，月球的物质平均比地球的物质松，但比构成太阳的物质更密。