田间持水量的推算与验证

一、理论推导

根据式（1.2）所示，单位质量的土壤其质量含水量可以表示为

式中，w为土壤质量含水量（g·g-1）；wpw为土壤萎蔫系数（g·g-1）；ws为土壤饱和持水量（g·g-1）；σ为水的表面张力系数（g·s-2）；ω为土壤孔洞周围固相颗粒的湿润角（°）；ε为形状排列系数；g为重力加速度（cm·s-2）；h为土壤水吸力（cm）；kV表示单个土壤孔洞的体积（cm3）；kS为单个土壤孔洞的表面积（cm2）。

如果土壤孔洞为球形，则kV和kS的计算公式为

式中，r为土壤孔洞的半径（cm）。将式（1.11）和式（1.12）代入式（1.2）得：

在20 °C时，土壤水吸力与土壤孔洞半径的关系为

联合式（1.13）和式（1.14）得：

将σ = 72.75 g·s-2、g = 981 cm·s-2、ω = 0°代入式（1.15）得：

式中，FCw即土壤田间持水量（g·g-1）。

联立式（1.16）和式（1.9），可得：

式（1.17）即不同土壤容重情况下土壤毛管持水量的理论计算公式。

二、公式验证

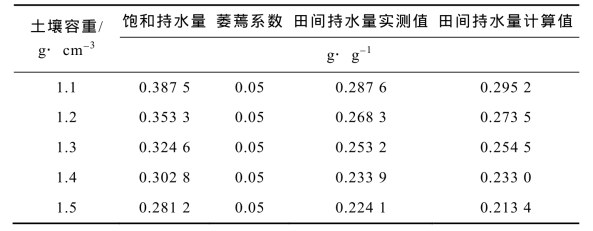
以轻壤土为例，检验田间持水量理论计算公式推算结果的准确性。土壤容重、饱和持水量、萎蔫系数、实测田间持水量和计算田间持水量数据列于表1-4。田间持水量实测值与计算值的平均数分别为0.219 4 g·g-1和0.223 9 g·g-1，统计分析表明二者间差异不显著（P ＞ 0.05）。

表1-4　轻壤土土壤水分常数

另外，将田间持水量的实测值与计算值进行线性回归分析。两者间的线性关系如图1-5所示。田间持水量的实测值与计算值间的线性回归方程为Y=1.004X（R2=0.952 8）。本例中，方程斜率与决定系数分别为1.004和0.952 8，二者均非常接近1.0。这表明田间持水量的计算值与实测值非常接近，可以认为是相等的。因此，本节推导的田间持水量的理论计算公式是正确的。

使用黑土、草甸黑土、碳酸盐草甸黑钙土、草甸土、草甸黑钙土和碳酸盐草甸土6种类型土壤的田间持水量数据（见表1-5）对式（1.17）进行检验。6种类型的土壤的田间持水量实测值的平均值分别为0.329 3、0.354 0、0.278 3、0.314 5、0.308 0和0.308 3 g·g-1，其对应的计算值的平均值分别为0.337 9、0.352 2、0.268 3、0.303 5、0.334 3和0.329 8 g·g-1。统计分析表明，实测值与计算值间差异不显著，因此，在统计学意义上可以认为实测值与计算值相等。这表明本节推导的田间持水量理论计算公式是可行的，可以用于土壤田间持水量的计算。

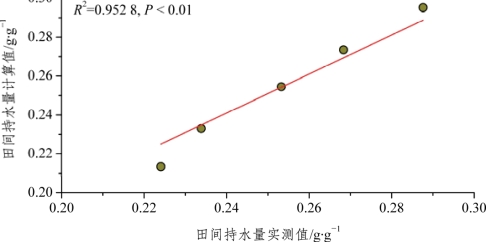
图1-5　轻壤土田间持水量计算值与实测值关系

表1-5　6种类型土壤田间持水量数据

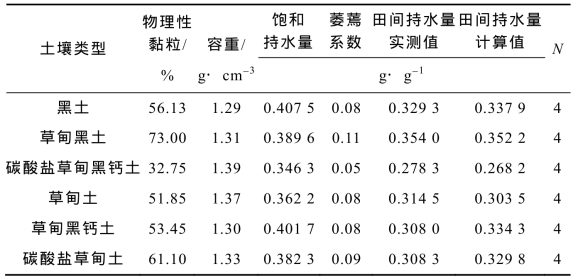
注：表中数据引自常兴义《黑龙江省主要土壤的田间持水量经验公式推求》，1979。

黑土、草甸黑土和碳酸盐草甸黑钙土实测田间持水量与计算田间持水量的线性回归分析见图1-6，草甸土、草甸黑钙土和碳酸盐草甸土田间持水量实测值与计算值的线性回归分析见图1-7。

图1-6　黑土、草甸黑土和碳酸盐草甸黑钙土田间持水量实测值与计算值关系

注：图中数据引自常兴义《黑龙江省主要土壤的田间持水量经验公式推求》，1979。

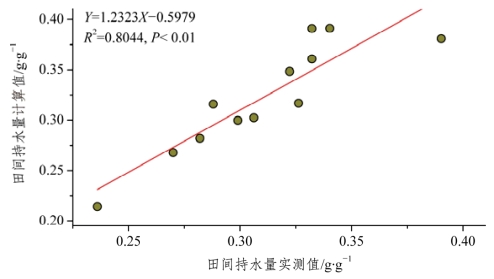
图1-7　草甸土、草甸黑钙土和碳酸盐草甸土田间持水量实测值与计算值关系

注：图中数据引自常兴义《黑龙江省主要土壤的田间持水量经验公式推求》，1979。

由图1-6和图1-7可知，土壤田间持水量实测值与计算值间存在极显著的线性关系。如果将方程形式变为Y=kX型，则应为Y=0.997 6X（R2=0.904 4，P ＜ 0.01）和Y=1.042 4X（R2=0.785 0，P ＜0.01）。方程斜率非常接近1.0，而决定系数R2 ＞ 0.78。这表明计算值与实测值非常接近。因此，本节推导的田间持水量理论计算公式可以用于实践工作。