毛管断裂含水量与土壤水分特征曲线的关系

一、理论假设

就土壤毛管断裂含水量与土壤水分特征曲线的关系，本节提出如下假设：土壤毛管断裂含水量等于土壤比水容量曲线拐点对应的含水量（简称比水容量拐点含水量）。该假设具体推导过程如下。

① 土壤毛管断裂含水量也称为生长阻滞点，其含义是当土壤含水量降低到毛管断裂含水量时，作物生长发育开始受到阻碍。

② 土壤比水容量随土壤含水量的降低（土壤水吸力的增大）而降低，当比水容量降低到拐点时，土壤供水能力会产生突变，这时作物吸水困难，生长受阻，此时土壤含水量应该为生长阻滞点。

③ 根据①和②的论述，土壤毛管断裂含水量等于土壤比水容量曲线的拐点含水量。

④ 在所有土壤水分特征曲线模型当中，仅van Genuchten模型的比水容量曲线可以求得拐点。

⑤ 由于土壤田间持水量等于以水吸力自然对数为自变量的van Genuchten模型的拐点含水量，因此，毛管断裂含水量对应的比水容量曲线拐点含水量也应该由以水吸力自然对数为自变量的比水容量曲线求得。

⑥ 比水容量拐点含水量的计算公式为

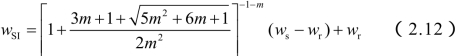
式中，SIw（g·g-1）为比水容量拐点含水量；wr（g·g-1）为残余含水量；ws（g·g-1）为土壤饱和持水量；m为土壤水分特征曲线van Genuchten模型参数。此处值得注意的是，m为以土壤水吸力为因变量的van Genuchten模型参数，即van Genuchten模型表达式为

⑦ 根据毛管断裂含水量的表达式（1.22），联合式（2.12），可得：

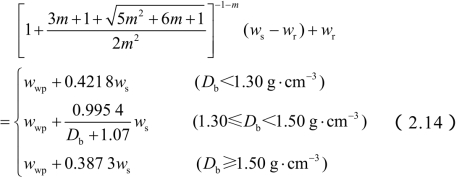
式（2.14）为不同容重状态下土壤毛管断裂含水量与土壤比水容量曲线拐点含水量的关系式。

二、假设验证

用162份土壤的水分特征曲线数据对本节提出的毛管断裂含水量和土壤比水容量拐点含水量的假设关系进行验证。土壤水分特征曲线的统计数据见表2-1。式（2.12）计算的土壤比水容量拐点含水量（SIw）与式（1.22）计算的土壤毛管断裂含水量理论推导值（RCw）间的线性关系见图2-7。如图2-7所示，土壤比水容量拐点含水量与毛管断裂含水量间存在极显著（P＜ 0.01）的线性关系。理论上，如果毛管断裂含水量完全等于比水容量拐点含水量，则线性方程的斜率和决定系数均等于1.0。本例中，方程的因变量分别等于0.824 4和0.946 5，二者均接近1.0。这表明比水容量拐点含水量与毛管断裂含水量数值非常接近。因此，本节提出的理论假设是正确的。

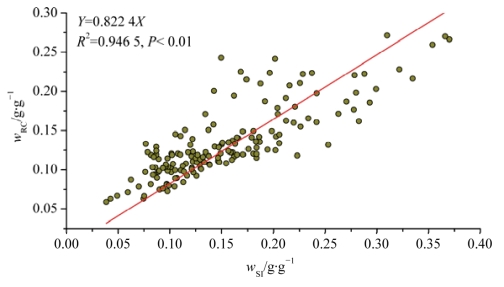
图2-7　土壤毛管断裂含水量（RCw）与土壤比水容量曲线拐点含水量（SIw）的关系（162份土壤）

另外，土壤比水容量拐点含水量与土壤水分特征曲线拐点含水量的关系见图2-8（a），土壤毛管断裂含水量与土壤田间持水量的关系见图2-8（b）。由图2-8可见，土壤比水容量拐点含水量与土壤水分特征曲线拐点含水量间存在极显著的线性关系，其线性方程斜率等于0.767 6；土壤毛管断裂含水量与田间持水量间也存在极显著线性关系，其方程斜率等于0.711 7。两斜率数值相差不大。

第二章第二节已经证明土壤水分特征曲线拐点含水量等于土壤田间持水量，而土壤比水容量拐点含水量和毛管断裂含水量分别占土壤水分特征曲线拐点含水量和土壤田间持水量的0.767 6和0.711 7。由于0.767 6非常接近0.711 7，可以近似认为相等，因此，毛管断裂含水量等于土壤比水容量拐点含水量，即本节提出的假设是正确的。

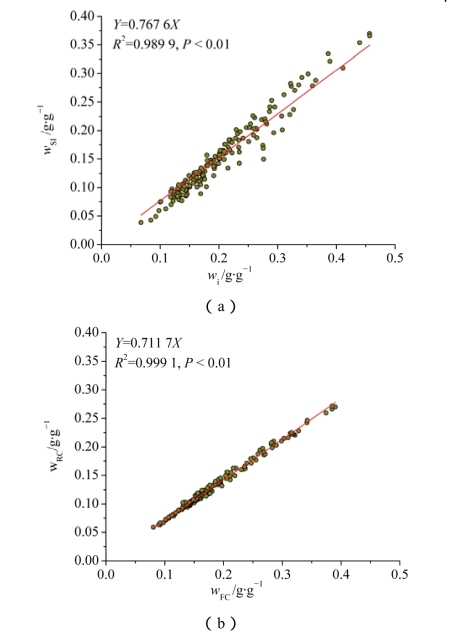
图2-8　土壤比水容量曲线拐点含水量（SIw）与土壤水分特征曲线拐点含水量（iw）的关系及土壤毛管断裂含水量（RCw）与土壤田间持水量的关系（162份土壤）

12种质地类型土壤的van Genuchten模型参数的统计分析数据（Carse1 and Parrish，1988；Schaap and Leij，1998）也被用于验证本节提出的毛管断裂含水量与土壤比水容量拐点含水量关系的理论假设。经过处理转换的土壤水分特征曲线参数和计算得到的毛管断裂含水量与土壤比水容量拐点含水量数据均列于表2-6。由土壤质地类型估算得到的萎蔫系数也列于表2-6。

由表2-6可知，各种质地类型土壤的比水容量拐点含水量与毛管断裂含水量非常接近。12种质地类型土壤的比水容量拐点含水量平均值为0.140 0 g·g-1，而毛管断裂含水量的平均值为0.143 0 g·g-1，统计分析表明，二者差异不显著。因此，比水容量拐点含水量与毛管水断裂含水量在统计学意义上是相等的。

表2-6　12种质地类型土壤的van Genuchten模型参数统计数据及计算的比水容量拐点含水量和毛管断裂含水量

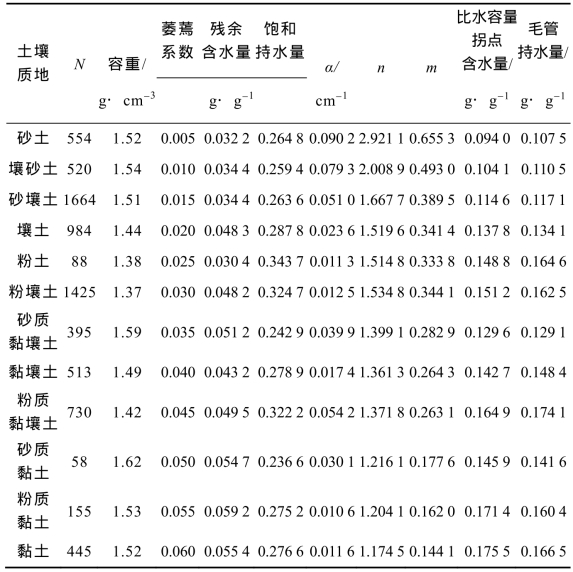
另外，土壤比水容量拐点含水量与毛管断裂含水量间存在极显著线性回归关系（见图2-9）。二者的线性方程为Y=1.016 2X（R2=0.849 9，P＜ 0.01）。方程斜率和决定系数均近似等于1.0。说明比水容量拐点含水量与毛管断裂含水量可以认为是相等的。

同时，12种质地类型的土壤比水容量拐点含水量与土壤水分特征曲线拐点含水量的关系见图2-10（a），土壤毛管断裂含水量与田间持水量的关系见图2-10（b）。两直线方程的斜率分别为0.711 8和0.722 6，决定系数分别为0.758 3和0.949 7，并且两方程均达到极显著水平（P ＜ 0.01），这些均表明本节的理论假设是正确的。

图2-9　12种质地类型土壤的毛管断裂含水量（RCw）与土壤比水容量曲线拐点含水量（SIw）的关系

另外，5种质地类型土壤的van Genuchten模型参数数据及由此计算的比水容量拐点含水量和毛管断裂含水量数据列于表2-7。这些数据也被用于验证本节提出的假设。

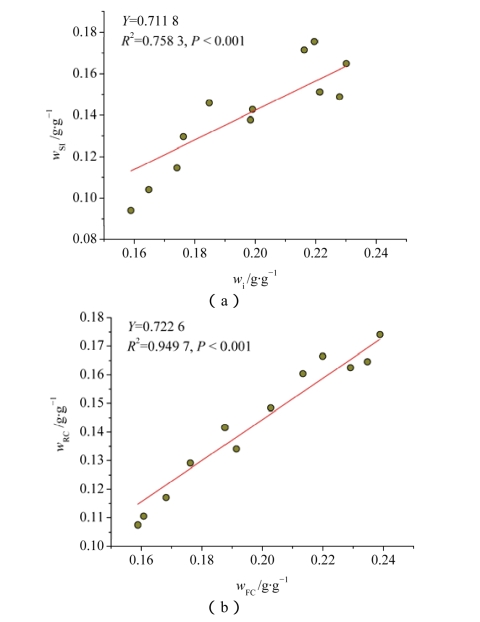
图2-10　土壤比水容量曲线拐点含水量（SIw）与土壤水分特征曲线拐点含水量（iw）的关系及土壤毛管断裂含水量（RCw）与土壤田间持水量（FCw）的关系（12种土壤质地类型）

表2-7　5种质地类型土壤的van Genuchten模型参数统计数据及计算的比水容量拐点含水量和毛管断裂含水量

续　表

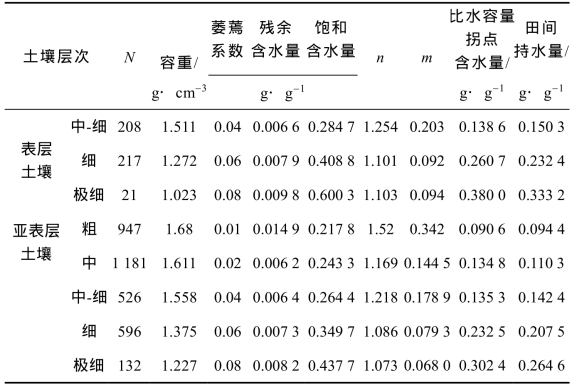
注：表中土壤van Genuchten模型参数统计数据引自Wösten et a1. Deve1opment and use of a database of hydrau1ic properties of European soi1s[J]. Geoderma, 1999。

由表2-7可知，由van Genuchten模型参数计算的比水容量拐点含水量和毛管断裂含水量数值非常接近。二者的平均值分别为0.195 0 g·g-1和0.179 9 g·g-1。统计分析表明，二者的平均值间差异不显著（P ＞ 0.05）。比水容量拐点含水量和毛管断裂含水量间存在极显著的线性相关关系（见图2-11）。线性方程斜率和决定系数分别等于0.896 8和0.971 2，非常接近1.0。土壤比水容量拐点含水量与土壤水分特征曲线拐点含水量的关系见图2-12（a），土壤毛管断裂含水量与土壤田间持水量的关系见图2-12（b），两直线斜率分别为0.777 8和0.728 0，二者非常接近。这表明比水容量拐点含水量和毛管断裂含水量两者在统计学意义上可以认为是相等的。因此，本节提出的理论假设是正确的。

图2-11　5种质地类型土壤van Genuchten模型参数计算的毛管断裂含水量（RCw）与土壤比水容量曲线拐点含水量（SIw）的关系

图2-12　土壤比水容量曲线拐点含水量（SIw）与土壤水分特征曲线拐点含水量（iw）的关系及土壤毛管断裂含水量（RCw）与土壤田间持水量（FCw）的关系（5种土壤质地类型）

本章小结

本章提出并验证了土壤毛管持水量、田间持水量和毛管断裂含水量与土壤水分特征曲线van Genuchten模型的关系。土壤水分特征曲线van Genuchten模型的表达式为

式中，w为土壤质量含水量（g·g-1）；wr为残余含水量（g·g-1）；ws为饱和持水量（g·g-1）；α为与土壤平均孔隙半径有关的参数（cm-1），1/α即为进气吸力值；h为土壤水吸力（cm）；m和n为曲线形状参数，并且m =1-1/n。土壤水分常数与土壤水分特征曲线van Genuchten模型的关系如下。

（1）当h = 1/α时，其所对应的土壤含水量即毛管持水量，因此，毛管持水量的土壤水分特征曲线计算表达式为

式中，wMC为土壤毛管持水量（g·g-1）；wr为残余含水量（g·g-1）；ws为饱和持水量（g·g-1）；m为土壤水分特征曲线van Genuchten模型的形状参数。

（2）土壤田间持水量是以土壤水吸力自然对数为自变量的van Genuchten模型曲线拐点对应的含水量（简称拐点含水量），其计算公式为（Dexter，2004）

式中，wFC为土壤田间持水量（g·g-1）；wr为残余含水量（g·g-1）；ws为土壤饱和持水量（g·g-1）；m为土壤水分特征曲线van Genuchten模型参数。

（3）土壤毛管断裂含水量等于土壤比水容量曲线拐点对应的含水量，其计算公式为

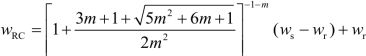
式中，wRC为土壤毛管断裂含水量（g· g-1）；wr为残余含水量（g· g-1）；ws为土壤饱和持水量（g· g-1）；m为土壤水分特征曲线van Genuchten模型参数。