【摘要】:假设在一个共同体内只有A、B两个地方政府。为了本地区的对外形象及其他方面的目的,A、B两地方政府均想建设某基础设施项目;然而由于该基础设施项目有较大的外部效应,因此在共同体内只要有一个便足够。现假定A、B地方政府只有两种战略选择:建设与不建设,据此,便可建立起二者的博弈模型。表4-6 支付改变后的基础设施建设的博弈模型
基础设施重复建设与完全信息条件下的静态博弈_基于区域扶贫开发视野的乡村旅游可持续发展问题研究
假设在一个共同体内只有A、B两个地方政府。为了本地区的对外形象及其他方面的目的,A、B两地方政府均想建设某基础设施项目;然而由于该基础设施项目有较大的外部效应,因此在共同体内只要有一个便足够。现假定A、B地方政府只有两种战略选择:建设与不建设,据此,便可建立起二者的博弈模型(表4-5)。
表4-5 基础设施建设的静态博弈模型

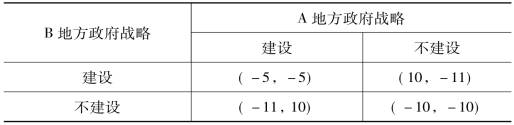
在这个博弈模型中,如果两者均选择建设,那么获得的支付就都为-5;而如果一方选择建设,另一方选择不建设,则选择建设者获得的支付为10,选择不建设者获得的支付为0;如果都选择不建设,则获得的支付都为0。显然,在这个博弈模型中,有两个纳什均衡:(建设,不建设);(不建设,建设)[49]。不过,由于现实中的地方政府常常处于相互竞争中,加之出于对自身政绩的关心,它们不仅不把二者均选择建设时的损失看得很重[50],反而十分看重选择不建设情况下的损失[51];这样,由于支付改变,博弈模型的结果也会发生相应的调整(表4-6)。从支付改变后的博弈看,纳什均衡就只有一个:(建设,建设)。这既是现实中的博弈均衡结果,又说明了如果不改变实践中的相关支付结构[52],那么重复建设的局面便难以避免。
表4-6 支付改变后的基础设施建设的博弈模型
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















