关于质能相当性定律的下面这个推导，以前未曾发表过，它有两个优点。尽管它用到了狭义相对论的原理，但不必预先要求这个理论的形式结构，而只用到三条事先已知的定律：
（1）动量守恒定律。
（2）辐射压的表示式；那就是在一固定方向运动着的一组辐射的动量。
（3）关于光行差（地球的运动对于恒星表观位置的影响——布雷德利（Bradley））的著名表示式。
我们现在考查如下这样一个体系。设物体B相对于〔坐标〕系K0来说在空间中是自由地静止的。两组各有能量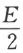
的辐射S和S′分别沿着正的和负的x0方向在运动着，最后都被B吸收了。由于这种吸收，B的能量增加了E。因为对称的缘故，物体B对于K0仍然是静止的。
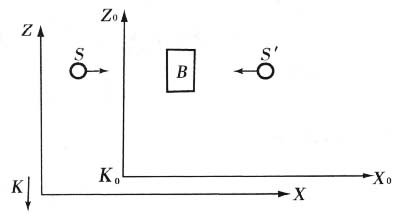
现在我们从〔坐标〕系K来考查这同一过程。K对于K0是以恒定速度υ沿着负z0方向运动着。对于K来说，这一过程的描述如下：
物体B沿正Z方向以速度υ运动着。两组辐射的方向，现在对于K都同x轴作一交角α。光行差定律说：在第一级近似中，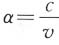
，此处c是光速。从K0来看，我们知道B在吸收S和S′时，速度ν保持不变。
现在我们把关于z方向的动量守恒定律用到坐标架K中的我们这个体系上。
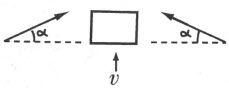
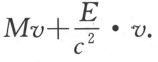
Ⅱ．吸收之后，设M′是B的质量。我们这里先预料这样的可能性：质量随着能量E的吸收而增加（为了使我们考查的最后结果贯彻一致，必然要如此）。体系在吸收后的动量因而是
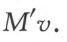
我们现在假定动量守恒定律成立，并且把它用到z方向上去。这就得出了方程
或者
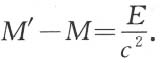
这个方程就表示质能相当定律。能量增加E同质量增加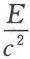
联系在一起。按照通常的定义，既然能量还留下一个附加常数未定，我们就可以适当选取这个附加常数，使
————————————————————
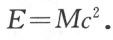
(1) 此文最初发表在1946年1月于纽约出版的《技术杂志》（Technion Journal，是海法（Haifa）希伯来工学院美国协进会的年刊），第5卷，16—17页。这里译自《晚年集》，116—119页。——编译者
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
