蒙提霍尔悖论
这个难题可追根溯源至贝特朗箱子悖论,它同时也是阐释“条件概率”的典型范例之一。这个悖论的基础是另一个较早期的问题,称为“三个囚犯问题”,由美国数学家马丁·加德纳于1959年在其《科学美国人》杂志的“数学游戏”专栏里提出。而蒙提霍尔悖论是我觉得更好、更清晰易懂的改编版本。这个难题最初是历久不衰的美国电视游戏节目《我们来做个买卖》里的一个游戏脚本,该节目是由超人气、加拿大裔的蒙地·霍尔(Monte Hall)所主持,因此被冠以此名。他在踏入综艺界之后改名叫蒙提(Monty)。
史蒂夫·谢尔文是美国统计学家,担任加州大学伯克利分校教授一职。他同时也是著名的教育家,曾因卓越的教学与对学生的优异指导而获奖。身为一名学者,他的专长是数学在医药方面的应用,特别是生物统计领域。然而他之所以举世闻名却不是归功于重要的学术成就,而是因为所撰写的一篇关于蒙提霍尔悖论的有趣文章。这篇文章发表于学术期刊《美国统计学人》 1975年2月号,只有半页篇幅。
谢尔文也许从来没有想过他的短文会带来如此大的回响,毕竟《美国统计学人》是一本专门期刊,主要读者为学术研究与教育人员。事实也是如此——足足过了15年,这个由他提出并加以解决的问题才广为人知。 1990年9月,号称发行量高达数千万份的美国周刊《大观杂志》的一位读者,向杂志里的专栏《玛丽莲答客问》提出一个问题。玛丽莲·沃斯·莎凡特负责在这个专栏回答读者提出的各种问题,包括数学益智问题、脑筋急转弯、逻辑机智问答等。莎凡特在1980年代中期因为跻身吉尼斯世界纪录中的智商纪录保持人(测验结果为185)而成名。提问的读者名叫克雷格·F. 惠塔克,他向莎凡特提出的问题基本上是谢尔文“蒙提霍尔悖论”的改编版。接下来的发展则让人始料未及。
这个问题与莎凡特的答复在《大观杂志》刊出之后,引起举国、甚至举世的注意。她的解答彻底违背直觉,却跟谢尔文原本的答案一样,完全正确。不过该杂志随即收到众多恼怒的数学家来函,迫不及待想证明她的错误。以下段落摘录自其中三封信:
身为一位专业的数学家,我对于一般大众缺乏数学技能感到非常忧心。请帮帮忙:承认你的错误,以后更小心一点。
你搞砸了,而且是在全国读者面前!看来你连当中的基本原理都没弄懂……这个国家的数学文盲已经够多了,我们不需要全世界智商最高的人为我们制造出更多。真丢脸!
在你再度回答这类的问题之前,建议你先找一本概率论教科书读一读,好吗?
我非常惊讶,在被三位以上的数学家纠正之后,你竟然还弄不清楚自己错在哪里。
也许女人看待数学的方式跟男人不同吧。
怒气冲天的人还真不少,然而随后的局面却令他们颜面无光。莎凡特在稍后发行的杂志中重新检视这个问题,她坚守立场,并为其解答提出清晰明确的解释与结论——正如读者预期一位智商185的人会做的事。整个故事最终登上《纽约时报》的头版,而争论依旧如火如荼地进行。
也许上述故事让各位读者开始觉得这个悖论甚为困难,只有天才才能破解。其实不然;有许多简单的方法能够加以解释,网络上也充斥各类讨论文章与部落格,甚至还有YouTube影片。
不论如何,暂且让揶揄与讲古在此打住,我们直接进入主题吧。我认为最好的方式乃是引述谢尔文刊登于1975年《美国统计学人》充满趣味的原文:
一个关于概率的问题以下出自《我们来做个买卖》,由蒙提·霍尔主持的著名电视秀节目。
蒙提·霍尔:这里有三个标记为A、 B、 C的盒子,其中一个里面有1975年出厂、全新的林肯·大陆汽车的钥匙,另外两个是空的。如果你选中的盒子里有钥匙,就能赢得这部汽车!
参赛者:(倒吸一口气)!
蒙提·霍尔:请挑选一个盒子。
参赛者:我选盒子B。
蒙提·霍尔:现在桌上有盒子A和C,然后这是盒子B (被参赛者紧紧抓住),汽车钥匙有可能就在这个盒子里!我出一百美元换你的盒子。
参赛者:不要,谢谢。
蒙提·霍尔:两百美元如何?
参赛者:不行!
观众:不要!
蒙提·霍尔:别忘了钥匙在你盒子里的概率是三分之一,盒子是空的概率则是三分之二。我出五百美元跟你换。
观众:不要!!
参赛者:不,我想保留这个盒子。
蒙提·霍尔:我来帮你打开桌上其中一个盒子(打开盒子A)。这盒子是空的!(观众鼓掌)。现在,车钥匙不是在盒子C、就是在你手上的盒子B里。既然只剩两个盒子,钥匙在你选的盒子里概率就变成二分之一了。我愿意出一千美元换你的盒子。
慢着!!!
蒙提的说法是正确的吗?参赛者知道桌上的盒子至少有一个是空的,他现在知道是盒子A了。这些信息是否令他选出的盒子里有钥匙的概率从三分之一变成二分之一?桌上的盒子其中一个必定是空的,蒙提是否借着透露哪个盒子是空的,帮了参赛者一把?赢得汽车的概率是二分之一还是三分之一?
参赛者:我想用我的盒子B 跟你交换桌上的盒子C。
蒙提·霍尔:这就怪了!!
提示:参赛者知道自己在做什么!
史蒂夫·谢尔文
加州大学公共卫生学院
伯克利,加州 94720
在以上的文章里,谢尔文略过了这个问题的关键(其重要性稍后就会厘清)。他没有明说的是,蒙提·霍尔知道钥匙在哪个盒子里,因此他总是能打开空的盒子。不过平心而论,他确实引述了蒙提所说的:“我来帮你打开桌上其中一个盒子。”我把这句话解释成:蒙提·霍尔完全知道他即将打开的盒子是空的。果真如此的话,那么这就是我所熟悉的问题了。稍后我们将会明白,问题的解答系建立在“蒙提·霍尔知道钥匙在哪里”的前提上,虽然这个前提看似无关紧要——毕竟对参赛者来说,这怎么可能会影响猜中的概率呢?
谢尔文不得不在1975年8月号的《美国统计学人》里特别澄清这一点,无法接受其解答的其他数学家不断批评他,正如莎凡特15年后的遭遇。他写道:
我收到许多来函,评论我在《美国统计学人》 1975年2月号《致编辑函》里,题为《一个关于概率的问题》的文章。有几位来函者认为我提供了错误的答案。我所提出答案的基本假设,乃是蒙提·霍尔知道钥匙放在哪个盒子里。
厘清这个关键之后,我们就能更仔细地探讨这个问题。接着我们来看刊登于《大观杂志》长度较短也较著名的版本。在这个版本里,三个箱子换成三道门,以下略经修改:
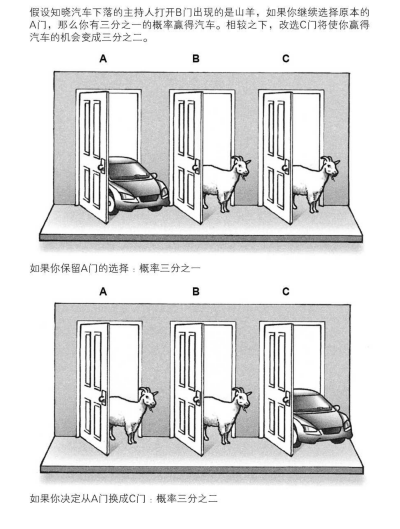
假如你是游戏节目的来宾,主持人提供的选项为A、 B、 C三道门。其中一道门后面有部汽车,另外两道门后面则是山羊。你挑选其中一道门,假设是A好了。接着,知道门后藏了什么的主持人打开另一道门,比如B,出现一只山羊。他问:“你想换成C门吗?”请问改变原本选择的门,是否对你较有利?
当然这个问题的前提是:参赛者喜欢汽车更甚于山羊,不过题目里并没有明说。我们假定参赛者并不是喜欢山羊的脚踏车骑士。
跟几年前谢尔文的答案一样,莎凡特的回答也认为参赛者应该要改变最初的选择,如此一来赢得汽车的机会将从三分之一倍增到三分之二。怎么可能会这样呢?这正是蒙提霍尔悖论的症结点。
当然,多数参赛者在面对这类抉择的时候,多半会怀疑其中是否藏有陷阱。既然大奖在每道门后的机会都相等,那么为什么不相信最初的直觉就好,继续坚持选择A门呢?对参赛者而言,汽车藏在A门或C门后面的概率看来当然是相等的,换或不换所选的门应该没有什么差别。
这一切实在晦涩难解并且令人困惑,可以想见为何连专业数学家都会弄错。以下提供几种解开这个诡局的方法。
检验问题的概率
以下所述的是最严谨、最有系统,也最无懈可击的方法,证明参赛者改变选择的门确实可以使赢得大奖的概率倍增。请记住,你原来选的是A门。蒙提·霍尔知道汽车在哪个门后面,他帮你打开另外两道门的其中一道,结果出现山羊,而且他还提供你换到C门的机会。
首先考虑继续选择A门的情形。
汽车藏在三道门之中任一道门后的概率是相同的:
● 当车子在A门后, B或C任一道门被打开:你赢了。
● 当车子在B门后, C门被打开:你继续选择A门,你输了。
● 当车子在C门后, B门被打开:你继续选择A门,你输了。
因此如果维持最初的选择,你有三分之一的概率赢得大奖。
接着考虑变更选择的情况。
汽车藏在三道门之中任一道门后的概率依旧相同:
● 当车子在A门后, B或C任一道门被打开:你输了。
● 当车子在B门后, C门被打开:由于你从A门换到B门,你赢了。
● 当车子在C门后, B门被打开:由于你从A门换到C门,你赢了。
因此变更选择之后,你有三分之二的概率赢得大奖。

无需数学证明:基本常识法
严格说来,以下非数学的方法并非真正的证明,只是让答案变得较令人能够接受。
假设现在不只有三道门,而是有1000扇门:其中一扇门后有一部汽车,其余999道门后面都是山羊。你随机从中选择一道门,比如第777号门。当然你可以任意选择喜欢的号码,但是不论如何,只要你不具备超能力,选中藏有汽车的门概率就是1‰。
接下来,知道汽车下落的蒙提·霍尔打开除了第238号门之外的其余998道门,里面全部都是山羊。现在,你面前有998只山羊以及两扇关着的门:你选的777号门,与尚未被打开的238号门。请问你要换,还是不换?
难道你不觉得,在那道被主持人保留、尚未开启的门后面,有令人起疑的东西——可能是一开始在随机挑选门时,主持人知道但你却无法获得的信息?别忘了,他掌握车子的下落。他看着你随机挑了一道(极)可能只有山羊的门,接着打开了另外998道藏有山羊的门。难道你不觉得非得换成仅剩的最后这道门不可?当然你会这么觉得,而且你猜得没错:几乎可以确定汽车是藏在蒙提特别保留下来的238号门后面。
改用较为数学的语言来说明:你最初的选择将门归入两个集合;集合一只有你选的门,汽车藏在里面的概率为三分之一(或者在前述较夸张的例子里,概率为1‰)。集合二包含所有其余的门,因此大奖之门落在这个集合里的概率就是三分之二(或者999‰)。集合二其中一道(或者998道)已知藏有山羊(亦即发现汽车的概率为零)的门被打开之后,这个集合里尚未打开的门只剩一道,而这道门里藏有汽车的总体概率仍旧是三分之二(或者999‰),因为它承继了车子落在这个集合里的概率。打开那些毫无价值的山羊之门,并不会改变汽车落在集合二里的概率大小。
先备知识扮演的角色
到这里,相信读者已经被说服了。不过万一你仍有任何挥之不去的疑问,以下提供另一个范例。我认为这个例子足以凸显具备先备知识与否的重大区别。
假设你想购买两只小猫。你打电话到附近的宠物店,老板说有两只同一胎出生的小猫在今天刚送达:一只黑猫,一只花猫。你向老板询问他们的性别,设想两种可能的回答:
(a)他告诉你:“我只检查了其中一只,是公的。”如果没有其他信息,两只小猫都是公的概率是多少?
(b)他告诉你:“我只检查了花猫,是公的。”这种情况下,两只小猫都是公的概率又是多少?
这两种状况的答案其实是不同的。虽然我们知道两者都至少有一只猫是公的,但只有在第二种情况里,我们才知道公的是哪只,而这正是改变概率大小的额外信息。以下我们来看看这个额外信息如何让概率产生变化。
首先,列出小猫性别的所有可能组合,共计四种:
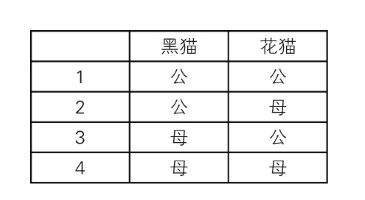
接着考虑状况(a)。“至少其中一只是公的。”意味着可能是前三种组合之一:(1)两只都公的;(2)黑猫是公的,花猫是母的;(3)黑猫是母的,花猫是公的。所以两只都是公的概率是三分之一。
然而,在状况(b)里你已经得知花猫是公的,这个额外信息除了排除第四种组合之外,同时也排除第二种组合。可能的组合只剩下两种:两只都是公的;或者花猫是公的,黑猫是母的。这种情况下,两只都是公猫的概率是二分之一。
因此可知,一旦你得知哪只猫是公的,两只都是公猫的概率立刻从三分之一变成二分之一。这跟蒙提霍尔悖论碰到的情形完全如出一辙。
但是且慢,我听到一些顽固的怀疑论者问道:“在小猫的故事里,宠物店老板已经将额外的信息告诉你,好让你算出概率大小。可蒙提·霍尔并没有做出相同的举动。”这个反驳意见带领我们来到整个解说的最后一部分。谢尔文1975年在《美国统计学人》的一文以及莎凡特1990年在《大观杂志》的解答曾经困惑许多读者,如今我们终于要揭晓其中的关键。我们得最后一次回到蒙提霍尔悖论。
假设蒙提·霍尔根本不知道车子藏在哪里。这时如果他打开B门出现山羊,你的确有相同的概率在A门或C门后面找到这部汽车。为什么会这样呢?想象我们重复玩150次这个三道门的游戏。每次游戏开始前,由一位独立裁判在三道门之间随机移动汽车,身为主持人的蒙提·霍尔也不知道车子的位置。如果让你先选一道门,蒙提·霍尔接着随机打开剩下两道门其中的一道,平均而言有三分之一的概率会出现汽车;从统计的角度来看,也就是150次当中有50次会出现汽车。在这50次,游戏当然就此结束;一旦你无法赢得汽车,游戏将不再继续下去。如此一来,蒙提·霍尔打开B门出现山羊,游戏得以继续进行的次数剩下100次。每一次,汽车有二分之一的概率藏在你最初选的门里,因此没有理由改变选择。也就是说,其中的50次你会发现汽车的确出现在你选的门里,另外50次则出现在C门里。再加上车子出现在蒙提打开的门后的50次,三种不同的情况各发生50次,意味着汽车出现在三道门后的可能性是相同的。
不过,如果蒙提知道车子的下落,他绝不会打开藏有汽车的门而浪费掉这50次游戏机会。总而言之,假设你每次都选A门好了, 150次当中有50次,汽车会出现在A门里,因此如果不换门的话,你有三分之一的机会赢得大奖。其余的100次当中,有50次汽车藏在C门里,蒙提打开B门;另外50次车子在B门里,他打开C门。在这100次的所有游戏中,蒙提总是打开藏有山羊的门,使得藏在另一个门后的车子不会出现。所以如果每次都改变选择,在这150次当中你将有100次赢得汽车,整体概率正好是三分之二。
一试便知
莎凡特在她最后一次探讨这个悖论的专栏里,公开了1000多所学校对此问题进行实作验证的结果。几乎所有结果都显示,换门才是正确的选择。这种“一试便知”的解答方式,也是我在几年前向朋友解释这个悖论时不得不采用的方法。那时我正为BBC制作一个电视科教节目,在搭车前往拍摄地点的漫长旅途中,我向摄影师安迪·杰克逊详述这个悖论。我得承认,当时自己还没想出上述的辩证与解释,因此只能拿出一迭色卡来示范。
我挑出三张卡片,一张红色两张黑色,洗牌之后将它们正面朝下,排列在我们之间的汽车座椅上。接着我小心翼翼偷瞄每张卡片的底面,以便确认红色卡片的位置。我请安迪挑选一张他认为是红色的卡片,但不要掀开。我接着掀开其余两张卡片中我确定是黑色的那张,再让安迪决定维持或更换所选的卡片。我们只试了不到20次就向他证明,如果改变选择的卡片,选到红色卡片的概率大约是不改变的两倍。他搞不太懂为何如此,不过至少相信我是对的。
我希望安迪能读到这一章,并且终于明白其中的原因。希望各位读者也是。
闲聊到此为止——还有9个正经的悖论在等着我们呢!
[1] 有一种叫作二项式系数的数学计算方法,在这个例子中应该是这样计算的:
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














