第八章 古希腊数学——欧几里得
这一章我们来讲古希腊的数学，那真是群星璀璨呢。
西方几乎每一门科学，就像文学、艺术与哲学等一样，都起源于古希腊。
—第一个数学家—
古埃及人与巴比伦人消失在历史的长河之后，在科学史上崛起并占据统治地位的就是古希腊人了。
无疑，古希腊人的数学知识，就像他们的天文学知识一样，最初是来源于古埃及人和巴比伦人的。
我们前面听说过的许多伟大哲学家和天文学家，例如泰勒士、毕达哥拉斯、柏拉图、亚里士多德、欧多克索斯、喜帕恰斯、托勒密等，同时也是数学家，甚至是了不起的大数学家，他们对数学的贡献不亚于其对天文学或者哲学的贡献。
泰勒士被认为是第一个伟大的几何学家，当然也是第一个伟大的数学家，就像他是第一个伟大的哲学家一样。
泰勒士第一件为人熟悉的数学成就要数他对金字塔高度的测量了。
金字塔高达100余米，又不能攀越上去，怎样才能知道它的高度呢？泰勒士想了一个好办法：他看到每年不同的季节人的影子是不同的，而到了秋分之后的某一天，影子的长度就会与金字塔的高度一样。这时候只要量一下金字塔影子的长度就会知道它的高度了。也许您会问：怎样才能知道哪天的影子长是同高度一样呢？这好办，你在太阳底下一站，看您的影子是不是同您的身高一样就行了。
从埃及回来后，泰勒士告诉大家的不只是金字塔的高度，还有一样更重要的东西：几何学。古希腊的第一个科学史家叫欧德谟斯曾写过一本《几何学史》，这本书现在已经失传。不过，另一位叫普罗克洛斯的，是雅典的柏拉图学院的导师，为这本《几何学史》写过一篇概要，现在却流传下来了。在《概要》中，他写道：
“泰勒士是到埃及去将这种学问（即几何学）带回希腊的第一人。他自己发现了许多命题，又将好些别的重要原理透露给他的追随者。他的方法有些是具有普遍意义的，也有一些只是经验之谈。”
据说由泰勒士发现或者从埃及带回来的命题主要有：
1.圆的直径将圆平分。
2.等腰三角形两底角相等。
3.两直线相交，对顶角相等。
4.有两角夹一边分别相等的两三角形全等。
最后一个定理的影响最大，现在人们还将用这种办法判明两三角形相等的定理叫泰勒士定理。
据说泰勒士还证明了半圆的圆周角是直角，这是第欧根尼说的，据说泰勒士发现这个之后，十分高兴，还按习俗宰了一头牛来庆祝。
—数的崇拜者—
泰勒士之后另一位伟大的数学家就是我们熟悉的毕达哥拉斯了。
毕达哥拉斯先是数学家，然后才是哲学家，因为他的哲学如我们前面所说过的一样，是从数学出发的。
例如毕达哥拉斯认为，万物都是数，是由数经各种各样的形式构成的。亚里士多德在《形而上学》第一章第五节中说道：
……在这些人之中，或在他们之前，有一些被称为毕达哥拉斯学派的人投身于数学研究，并最先推进了这门科学。经过一番研究，他们认为，数是一切存在的本原。
毕达哥拉斯还认为只有数才是和谐的、美好的。他找了各种各样的数，如长方形的数目、三角形的数目、金字塔形数目等，它们都是由一些数目小块构成的，具有美的形状。他还认为十是最完美的数，所以他认为天体的数目也应当是十。但那时人们能看到的只是九个，所以他又硬加了一个第十个，取名叫“对地”。
毕达哥拉斯的有些数学发现直到今天还在用着，如数的平方、立方这些词就是毕达哥拉斯造出来的。
毕达哥拉斯还提出了著名的“四艺”——算术、音乐、几何、天文。并且将这四艺都与数学联系起来。将第一艺算术称为“数的绝对理论”；将第二艺音乐称为“数的应用”；第三艺几何称为“静止的量”；第四艺“天文”称为“运动的量”。后面这“量”其实也是数，只是因为这数与具体的图形及天体挂钩起来了，因此称之为量。这四艺乃是毕达哥拉斯规定他的弟子们必须学习的四大课程，他称之为“四道”，即四条道路之意。这种学习内容被西方人沿用下来，直到中世纪，才又加上了三艺：文法、修辞、逻辑，合称“七艺”，是中世纪有文化的贵族子弟所必习之学问。大家知道，中国古代有六艺，即“礼、乐、射、御、书、数”，与西方的七艺中只有两项是共同的，即音乐和数学。由此可知，数学在古代东方与西方都受到人们高度的重视呢！
但毕达哥拉斯最有名的发现还是所谓的毕达哥拉斯定理，就是直角三角形的两直角边平方之和等于第三边的平方，这也就是中国的勾股定理。
我们前面讲巴比伦人的数学成就时，曾说过他们可能发现了类似勾股定理的三组数a2＋b2＝c2，毕达哥拉斯虽然也去过巴比伦，但不大可能是从巴比伦人那里剽窃来的。因为当毕达哥拉斯去巴比伦时，发现勾股定律的古巴比伦人——如果古巴比伦人确实发现了的话——连同他们的发现早已经消失在历史的长河中了，而他们留下来的泥板文书即使被当时的人发现了，也不可能读懂呢！
不过，由于对数字充满了崇拜，好像它们真的是神一样，传说毕达哥拉斯也做了一些不好的事。例如他的一个叫希伯斯的学生因为发现了无理数，曾被他威胁过不要将发现说出去，因为这个发现给他视之为神的数抹上了阴影。这数就是边长为1的正方形的斜边长，即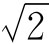
，这个数字正是根据毕达哥拉斯发现的勾股定理得出来的。
毕达哥拉斯之后，天文学家欧多克索斯也是一位了不起的数学家，例如他发现了比例理论，即等比定理。根据他的比例理论，人们更深刻地理解了什么是无理数，并且找到了一种方法，能够使无理数近似地表示为有理数。
比前面几个伟人更伟大的是欧几里得。
—伟大的“建筑师”—
欧几里得在古代数学史上享有无与伦比的大名，以至到现在数学都被分成两大部分：欧氏几何与非欧几何。所谓欧氏几何也就是欧几里得的几何，非欧几何当然就是非欧几里得的几何了。欧氏几何实际上囊括了我们平时所称的所有几何内容，也囊括了历史上绝大部分历史时期之内的几何，要知道，非欧几何直到约百年前才诞生呢！
为什么欧几里得如此有名？所谓欧氏几何真是他发明的吗？当然不是，实际上由他亲自发现的理论并不多，他与其说是一个伟大的发现者，不如说是一位伟大的收藏家：他大量搜集别人发现的几何学理论，加以理解、融会贯通，然后分门别类地整理，使之明确化、系统化。而在他的这种系统化之前，几何学是零散的，没有完整的体系，甚至没有所有理论都须基于之的公理。这样一来，几何学就像一堆没有建成屋子的砖头、水泥、木料之类。欧几里得来之后，经过一番辛勤劳动，将这些砖呀、水泥呀、木料呀建成了一座漂亮的房子。
欧几里得为几何学建成的房子名叫《几何原本》，简称《原本》，是整个古希腊数学的总结，也是几千年后几何学甚至整个数学的范本。
不过，在谈他的《几何原本》之前，我们还是先谈几句他的生平吧！
说实在的，关于欧几里得的生平与他的成就实在不成正比，一方面是他的名字如此有名，另一方面关于这个名字的主人的生平与事业后人却知道得如此之少。即使在知道得不多的东西里矛盾也很多，可谓众说纷纭。
首先，我们不知道欧几里得是什么地方人，只知道他大概是希腊人，因为他早年曾求学于雅典。这也不能确定，谁说小亚细亚诸多希腊城邦的希腊人，或者现在意大利南部那时称大希腊的希腊人不能去希腊文明的中心雅典学习呢？甚至于当时非洲北部的埃及等地也生活着许多希腊人，他们同样可以去雅典留学，欧几里得完全可能是这些地方的人。总之，关于欧几里得的出生地是一笔糊涂账，权威一点的书都不敢乱说的。当然，上述那些地方虽然地域不在希腊，但大部分都是希腊城邦，其人民讲种族而言也是希腊人，所以称欧几里得是希腊人总是没错的。
其次，我们也不知道他生活的精确年代。5世纪时，柏拉图学园的一个叫普罗克洛斯的导师，在他的一本书中说到，欧几里得是埃及托勒密一世时代的人。根据历史资料我们可以知道，托勒密一世于公元前323年到前285年在位。《概要》又说阿基米德曾引用过欧几里得的著作，我们又可以知道欧几里得活动的年代比阿基米德要早一些，而阿基米德大致的生活年代是知道的，是公元前2世纪。由这些可以推测欧几里得的活动时期是公元前300年左右。在这个时期里，可以肯定他生活于埃及的亚历山大，职业是一名数学教师，主要教授几何学。
除了这些，我们知道的就是有关欧几里得的几则趣闻轶事了。
一则是有次托勒密王问欧几里得，除了《几何原本》之外，还有没有其他学习几何学的捷径。欧几里得回答说：“几何无王者之道。”意思就是，在几何学里没有一条专供国王学习与轻松掌握之道，要学好几何学，唯一的途径就是像大家一样努力。这句话后来以“求知无坦途”的形式流传下来，成为西方的千古箴言。
另一则是某次欧几里得的一个才入门的学生问老师学了几何学有什么好处。欧几里得立即叫人给他三个钱币，说：“他想从学习中获取实利呢！”这句话的意思就是追求知识的目的不应该是获取钱财之类的实利，而应当是追求知识本身。
也许这正是欧几里得虽然在几何学里成就斐然，后人对他的生平事迹却知之甚少的缘故。因为他专心致志地研究科学，哪有闲工夫去为自己扬名呢！而且，即使在他的著作里，他也从来不自称是哪个公理定理的发现者或创立者，好像一切都是他人的功劳，他只是帮助整理了一下而已！在此我们应当再次向伟大的欧几里得致敬！
—数学之美的象征—
与欧几里得模糊的人生资料形成鲜明对比的是他在《几何原本》里表达的理论体系的明确。
首先我们要明白，《几何原本》不同于一般的科学著作，如托勒密的《天文学大成》或者哥白尼的《天体运行论》，它确实不是一本原创性很强的著作，而是一部前人几百年间科学研究成果的总结与系统化。
《几何原本》最早的本子早已失传，我们现在看到的都是后来的各种修订本或译本。很早以前，古希腊就有人对《几何原本》作过修订、整理和注释，从而出现了不止一种本子，其中最著名者是一个叫塞翁的人作的，他为《几何原本》作了仔细且比较全面的校订与注释，并且有所补充。后来这个本子成为几乎所有流行的本子的基础。但塞翁是约4世纪的人，这时候欧几里得已经去世七百来年了，所以他本子的准确性还有待考证。现在最早的本子也许是19世纪在梵蒂冈发现的，它是拿破仑从意大利带回来的无数文物战利品之一，据科学史家们考证，它可能比塞翁读过的本子还要古老。
我们知道，中世纪是一个黑暗的世纪，对科学研究尤其如此，那时大批科学古籍都在欧洲散失了。与此同时，阿拉伯人崛起强大，成为科学文化发达之地，那些阿拉伯学者们读到欧几里得的《几何原本》后，深感兴趣，将之译成了阿拉伯文。后来，当文艺复兴开始，欧洲人重新重视科学后，就从阿拉伯人那里找回了《几何原本》，将之再译成了当时欧洲的通用学术语言拉丁语。第一个完整的拉丁文本是在12世纪初由英国经院哲学家阿德拉德译出来的。
此后，欧洲人对《几何原本》表现出了莫大的兴趣，等到谷腾堡发明印刷术，印刷品流行后，印刷得最多的作品之一就是《几何原本》。据说到19世纪末，用各种版本印刷的《几何原本》达1千余种，也许是除了《圣经》之外印刷得最多的作品，至少是印刷得最多的科学作品。
目前，《几何原本》诸多版本中最为权威的是由L·海伯格和H·门格等合作出版的《欧几里得全集》中的本子，它对《几何原本》进行了相当全面的校订与注释，并且是希腊文与拉丁文的对照本。最好的英译本则是由希思根据海伯格本译出来的，书名《欧几里得几何原本13卷》，1908年出版。这本书的主要特色是有一个长达150多页的导言，导言中总结了有关欧几里得研究的历史，并对每章每节作了十分详细的注释。
除了这几个西方通行的语种外，《几何原本》作为西方也是人类历史上最重要的科学经典之一，世界上各大语种几乎都有它的译本，例如中国据说早在元朝时就有了译本或者节译本，第一个完整的译本出现于17世纪初，由著名的意大利来华传教士利玛窦与中国古代最伟大的科学家之一徐光启合译。
还有一点很有趣的是“几何”这词的译法，这是西词汉译里少有的音译与汉译俱到位的例子。几何之拉丁文是“geometria”，徐光启与利玛窦据之译为“几何”，是最前面两个音节的音译，同时，“几何”在汉语里又是多少之意，如“姑娘青春几何？”就是“姑娘你多少岁啦？”之意，这“多少”同时不言而喻也是所有数字乃至数学最基本的含意。这样音译与意译就完美地结合起来了。
《几何原本》共分13卷，第一卷又分为两节，第一节中首先给出了23个定义，例如什么是点与直线，什么是平面、直角、垂直、锐角、钝角等，这是几何学的最基本元素，对于这些元素，欧几里得没有用到任何公理与公设，因为它们甚至是比公理与公设更为基本的东西，只是一些直观的描述，连推理也没有，也不能有。
欧几里得给出的几个基本定义是：点是没有部分的东西，没有体积也没有面积或者长度等，总之，是一个抽象的点。线则是单纯的长度，没有宽度，它是由无数点无曲折地排列而成的。
给出定义之后，欧几里得提出了他著名的5个公设。
什么是公设呢？它与公理有什么不同？这是一个问题。一般认为，所谓公理是自然之理，它不仅存在于数学之中，也存在于不懂数学的普通人所具备的常识之中。公设则只存在于所要分析的学科之中，例如几何学的公设只存在于几何学之中，物理学的公设则只存在于物理学之中。
欧几里得共为几何学提出了5个公设：
1.给定两点，可连接一线段。
2.线段可无限延长。
3.给定中心和圆上一点，可作一个圆。
4.所有直角彼此相等。
5.如一直线与两直线相交，且在同侧所交的两个内角之和小于两个直角，则这两直线无限延长后必定在该侧相交。
这里要注意的是第二条公设，那里的线段实际上是我们所讲的直线。
五条公设里最不平凡的是第五条，它后来被称为平行公设或第5公设，有各种各样的表达形式，总之是说明什么情况下两直线平行与不平行。其最简明的表达法是：经过直线外一点，只能作一条直线与已知直线平行。
看得出来，这第五公设与前面四条公设比起来复杂不少，欧几里得在这里也没有证明，也许是他认为无需证明，也许是他不能证明。后来人们觉得这个公设应该证明，于是力图用前面的四条公设来证明第五公设，但都归于失败。于是有人干脆否定了它，其结果就是非欧几何了。
在5条公设之后欧几里得又提出了五个公理：
1.与同一个东西相等东西，彼此相等。
2.等量加等量，总量仍相等。
3.等量减等量，余量仍相等。
4.彼此重合的东西相等。
5.整体大于部分。
看得出来，这是比前面的5条公设更为简单的东西，是真正放之天下而皆准的“公理”。
在5条公理之后，欧几里得开始进一步提出命题，在第一卷里他共提出了48个命题，例如我们前面提过的泰勒士定理，即如果两个三角形的两边及其夹角分别相等，那么这两个三角形全等就是第4个命题。
第5个命题则是：等腰三角形两底角相等，两底角的外角也相等。由于在这里涉及了四个角，还有好多条线段与直线，因此在中世纪时，有些学生们学起来很是麻烦，老师教了很久也不明白，于是它便有了一个绰号“驴桥”，我们知道驴子是怕过桥的，尤其是当桥稍微有点儿窄或者不稳时，它就赖着不走了。现在，这“驴桥”喻指笨蛋的难关，这命题虽然有一点不好懂，但只有笨蛋才怕它，视它为难关。
在第二节中，欧几里得提出了与平行四边形、三角形等的面积相关的各命题。其中第47个命题就是著名的勾股定理，不过其形式不同于现在表达的勾股定理，它是这样表达的：“在直角三角形斜边上的正方形面积等于直角边上两正方形面积之和。”第48个，也就是第一卷最后一个命题则是勾股定理的逆定理。
第一卷是整部《几何原本》的基础，此后的诸卷就是以之为基础来论证的。它表达的清晰与论述的明白、逻辑的谨严也是整部《几何原本》的典范。有这样一个故事：据说英国著名的经验主义哲学家霍布斯有天偶然翻开了《几何原本》，随便看了几页，看到欧几里得的证明，觉得大不对头，怎么能够得出这样的结论呢？于是，他开始由后往前翻，看看这些证明的基础是什么，当他翻到最前面时，终于彻底信服了！《几何原本》论证之严密由此可见一斑。
前面我们比较详细地讲述了第一卷，一方面是因为第一卷是全书的基础与典范，另一方面也是将之作为一个例证，让我们大概看看欧几里得是怎么说他的几何学的。至于后面的几卷，就只能一带而过了。
第二卷比较短，只有14个命题。讲的是长方形的剖分，实际上则是用几何的方式来讲代数，是“几何代数学”。例如一个数就用一条有长度的线段来表示，两个数的乘积就说是长方形的面积，其两边分别是这两个数。
第三卷和第四卷主要是与圆有关的内容，第三卷包括圆、弦、圆的切线与割线、圆心角与圆周角，第四卷讨论了给定一个圆之后，如何只用直尺和圆规作它的内接和外切正多边形的问题。这些内容，尤其是第三卷，就是我们在中学平面几何中所要学习的内容。
第五卷是有名的精彩一卷，在这里欧几里得对欧多克索斯的比例理论作了十分精彩的解释与论证，被视为西方数学史上罕有的杰作。关于它还有一个故事：一个名叫布尔查诺的牧师兼业余数学家在布拉格治病。在浑身难受之时，顺手抄起了正在手边的一本《几何原本》，正好翻到第五卷，他读了欧几里得对欧多克索斯比例理论的精彩解说后，不由大感痛快，病一下子好了！后来，他一生病就读第五卷，书到病除，屡试不爽。
第六卷也与第五卷相关，主要是应用欧多克索斯的比例理论来讲各种相似的几何图形及其面积。
第七、八、九三卷讨论的都是同一类问题，即数论。我们前面已经讲过了数论，知道它们虽然常只与正整数相关，看上去比较简单，然而实际上内里却有着九曲回肠，复杂无比。例如哥德巴赫猜想到现在也未能证明。这三卷共有约100个命题。第七卷介绍了求一个或多个整数的最大公因子的办法，现在它被称为欧几里得算法。第八卷有所谓连比例及相关的几何级数。什么是连比例呢？就是下面形式的比例：a∶b＝b∶c＝c∶d，如果这样的比例成立，则a、b、c、d构成了几何级数。例如8∶4＝4∶2＝2∶1就是连比例和几何级数。在第九卷中欧几里得提出了许多有关数论的重要定理，例如“任何大于1的整数都能按（实质上）唯一的方式表示成一些素数之积”。并且证明了素数有无穷个。
《原本》的最后三卷，即第十一、十二和十三卷都是有关立体几何的。第十一卷讲空间中的平面、直线、垂直、平行、相交等关系，以及多面角、平行六面体、棱锥、棱柱、圆锥、圆柱、球等比较复杂的立体图形的体积计算等问题，特点之一就是通篇都用到了前面的平行公设。共有39个命题。
第十二卷则是对“穷竭法”的具体运用。所谓“穷竭法”，在这里就是指某一个图形，例如圆，被另一个图形，例如其内接正多边形，逐步“穷竭”，也就是慢慢地填满之意。此时这个正多边形的面积也就会越来越接近于圆的面积了。这是“穷竭法”最经典的运用。我们前面已经多次提及了这一方法。
最后一卷，即第十三卷，是有关正多面体的问题。
上面我们花不少篇幅讲了《几何原本》，之所以如此，不但是因为它是西方数学史上第一部经典，而且因为它也是典型的数学经典，从这里我们可以发现所有数学经典的影子，它就像标尺一样竖立在数学家们的眼前，像灯塔一样指引着他们的数学发现与探索之路。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
