岩体力学参数的三维离散元数值试验结果

基于4.4.1　节所建立的不同尺寸、不同位置的岩体模型，按4.4.2节给定初始应力边界条件，根据4.4.3节的方法设置岩块和结构面的本构模型和参数，利用FISH语言编程采用室内试验所得的结构面变形本构模型描述真实结构面的应力变形特征，按4.2.4节的三种数值试验设计方案进行各裂隙岩体模型力学参数的数值试验研究。下面以位置1处的最小尺寸岩体(4m×4m×4m)为例，说明数值试验法确定裂隙岩体力学参数的过程。

4.4.4.1　数值试验方案1

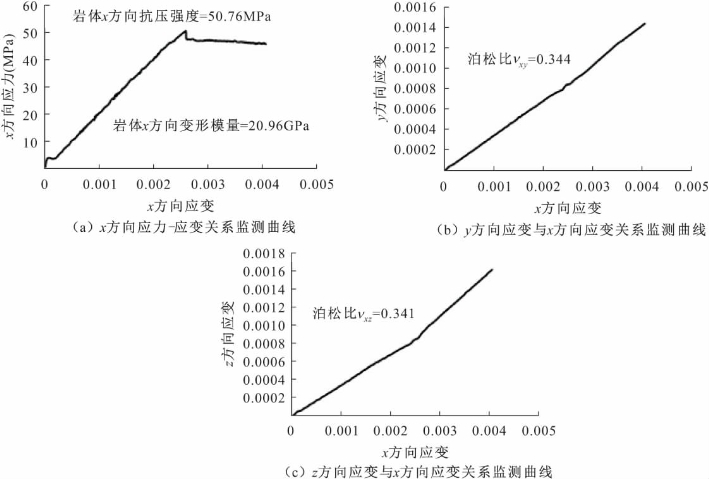
图4-14　岩体x方向加压所得应力应变监测曲线(4m×4m×4m，位置1)

如4.2.4节所述，数值试验方案1模拟岩体的压缩试验，用来确定岩体的抗压强度、强度参数(内聚力和内摩擦角)、变形模量和泊松比。首先在岩体模型(4m×4m×4m)的x、y和z方向分别施加大小为2.2MPa的压应力，然后保持两个方向的压应力不变，在另一个方向以0.05m/s的速度匀速加压直至模型破坏，这个匀速加压的过程分别在x、y和z方向重复。图4-14为x方向加压所得到的监测曲线。其中图4-14(a)为x方向应力应变监测曲线，如图所示，破坏前岩体的x方向应力和x方向应变基本呈线性增长，当x方向应力增加至50.76MPa时岩块发生破坏;破坏之后岩体呈塑性流动状态，应力不再增加而应变不断增长。根据该曲线的应力峰值，可确定岩体x方向的抗压强度为50.76MPa，根据50%峰值抗压强度处所对应的应力应变曲线的斜率确定岩体的变形模量约为20.96GPa。图4-14 (b)为y方向应变随x方向应变的变化关系曲线，利用50%峰值抗压强度时x方向应变值所对应的该曲线斜率确定该岩体泊松比νxy的值为0.344。图4-14(c)为z方向应变随x方向应变的变化关系曲线，同样利用50%峰值抗压强度时x方向应变值所对应的该曲线斜率确定岩体的泊松比νxz为0.341。图4-15为该岩体模型y方向加压所得到的监测曲线，同理可根据图4-15(a)确定岩体y方向的抗压强度和变形模量，根据图4-15(b)x方向应变与y方向应变关系曲线确定岩体的泊松比νyx，根据图4-15(c)z方向应变与y方向应变关系曲线确定岩体的泊松比νyz，各参数值如图4-15所示。图4-16为该岩体模型z方向加压所得到的监测曲线，同理可确定z方向的抗压强度、变形模量、泊松比νzx和泊松比νzy的值，各参数值如图4-16所示。为了估算岩体的粘聚力c和内摩擦角φ，将岩体的边界应力从2.2MPa增加至13.2MPa(6倍)，再按应力路径1将上述数值试验重复一遍，可分别得到高应力下该模型x、y和z方向的抗压强度。利用岩体模型两个破坏临界状态的应力值，结合P-Q法和Mohr-Coulomb法两种方法确定岩体的粘聚力和内摩擦角，该模型岩体x方向的粘聚力为10.48MPa，内摩擦角为39.5°;y方向的粘聚力为9.68MPa，内摩擦角为39.5°; z方向的粘聚力为9.81MPa，内摩擦角为39.5°。可见与完整岩块的强度参数相比，该岩体的粘聚力减小，内摩擦角基本无变化。

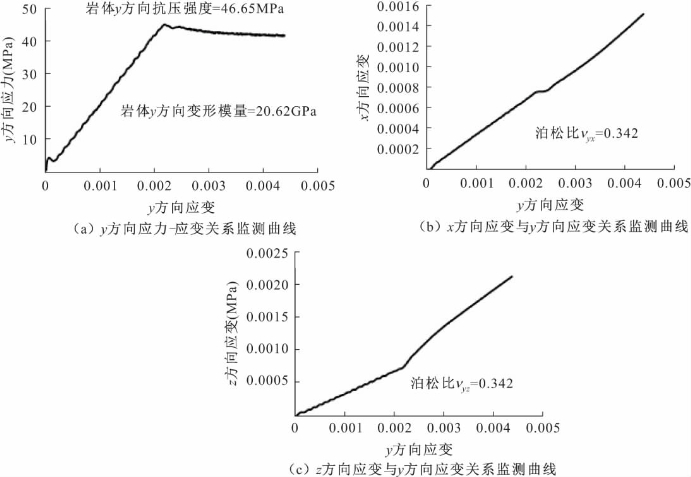
图4-15　岩体y方向加压所得应力应变监测曲线(4m×4m×4m，位置1)

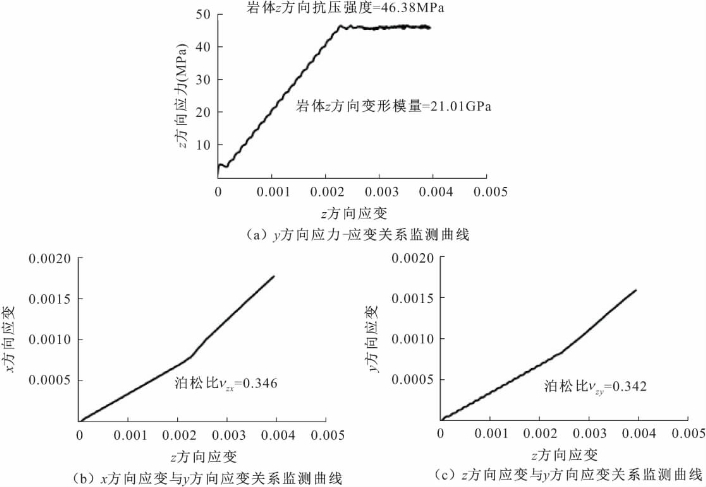
图4-16　岩体z方向加压所得应力应变监测曲线(4m×4m×4m，位置1)

以上基于数值试验方案1，估算出了位置1处的最小尺寸岩体模型(4m×4m×4m)的抗压强度、强度参数、变形模量和泊松比，利用同样方法也可获得其他4个随机选取的不同位置处该尺寸模型的力学参数，并求取该尺寸5个不同位置岩体模型的各力学参数的均值，作为该尺寸岩体(4m×4m×4m)力学参数的最终结果，如表4-6所示。

按照4.2.2节所述的非连续/等效连续混合研究方法，基于已获得的最小尺寸岩体平均力学参数，逐级确定较大尺寸岩体不同位置的平均力学参数，直至确定出最大尺寸岩体的力学性质。在此过程中，考虑岩体各向异性特征的影响，将岩体在x、y和z方向的力学参数尺寸效应研究分开进行，具体方法详见4.2.4节。按数值试验方案1所确定的各尺寸岩体在3个相互垂直方向上不同位置岩体模型的抗压强度、强度参数(粘聚力、内摩擦角)和变形模量的均值如表4-6所示。

由计算结果可知，岩体的内聚力随着岩体尺寸的增加而减小，而内摩擦角基本无变化，对其原因进行分析可知，岩石内摩擦角反映岩石矿物颗粒间的摩擦性质，研究所采用的岩块内摩擦角为39.5°，结构面的内摩擦角为33°，两者相差不大，而各级尺寸岩体中所包含的结构面尺寸与岩体尺寸相比较小且为非贯通状态，另外本书假设结构面平直光滑且闭合，结构面的内摩擦角对整个岩体的等效内摩擦角贡献可忽略不计，因此随着岩体尺寸的增加，岩体的等效内摩擦角基本无变化。另外，假设岩体抗拉强度随岩体尺寸变化的折减系数与内聚力的折减系数一致，不同尺寸岩体在3个相互垂直方向加压所求得的泊松比数值如表4-7所示。

表4-6　数值试验方案1确定的不同尺寸岩体力学参数值

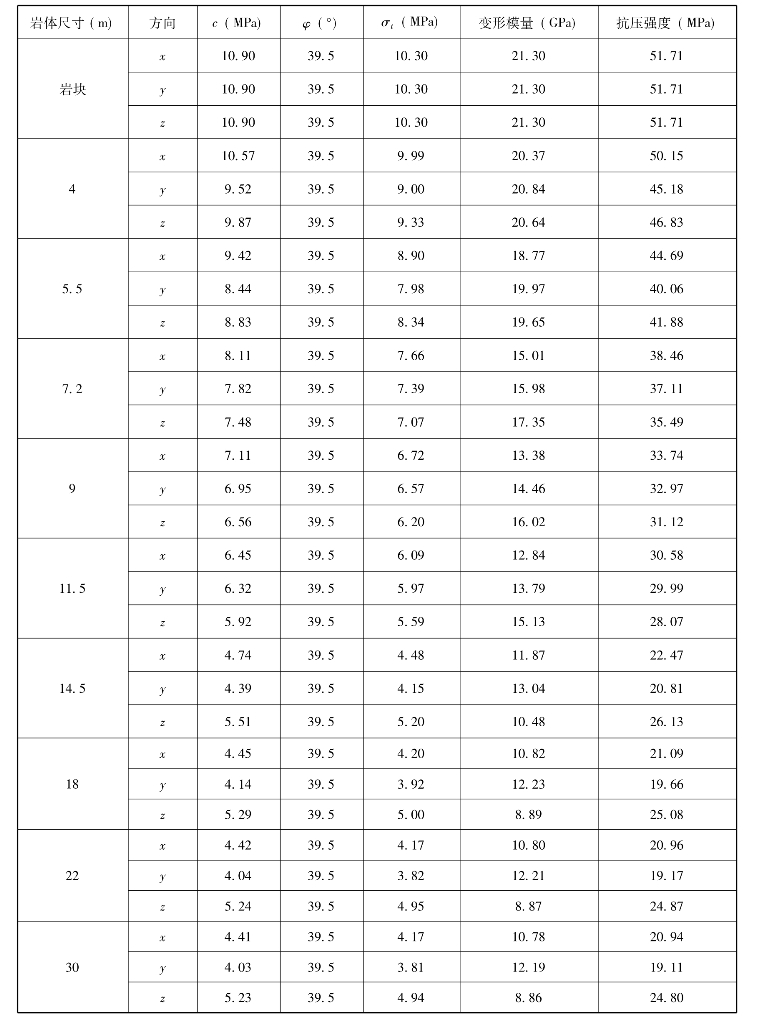
注:岩块的变形模量为杨氏模量;表中所有岩体力学参数值均为不同位置该尺寸模型计算所得的均值。

表4-7　数值试验方案1所确定的不同尺寸岩体泊松比

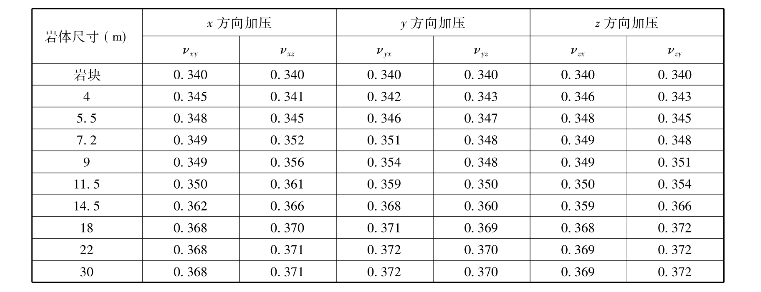
注:表中所有泊松比数值均为不同位置该尺寸模型计算所得的均值。

4.4.4.2　数值试验方案2和方案3

分别采用数值试验方案2和方案3估算位置1处的最小尺寸岩体(4m×4m×4m)的剪切模量和体积模量。首先在岩体x、y和z方向分别施加大小为2.2MPa的压应力，然后在模型xy平面施加均匀增加的剪应力，监测加载过程中各监测点的应力应变情况，计算得出该岩体xy平面上的剪切模量7.16GPa。加压过程分别在xz平面和yz平面重复，可确定岩体在xz平面和yz平面的剪切模量分别为6.87GPa和7.68GPa。然后采用应力路径3估算该模型岩体的体积模量，同样首先在岩体x、y和z方向上分别施加大小为2.2MPa的压应力，然后在各个方向上同时均匀增大压应力，记录各监测点的应力应变情况，求得该尺寸岩体的体积模量为20.81GPa。然后对其他位置的最小尺寸岩体重复上述过程，求取不同位置模型剪切模量和体积模量的均值作为该尺寸模型的最终剪切模量和体积模量值，同样基于非连续/等效连续混合研究方法，利用已获得的最小尺寸岩体平均剪切模量和体积模量，逐级确定较大尺寸岩体不同位置的平均剪切模量和体积模量，直至确定出最大尺寸岩体的参数值。不同尺寸岩体剪切模量和体积模量数值试验结果如表4-8所示。

表4-8　不同尺寸岩体剪切模量和体积模量数值试验结果

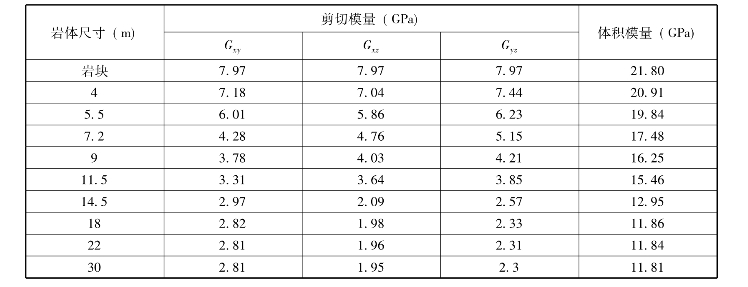
注:表中所有剪切模量和体积模量数值均为不同位置该尺寸模型计算所得的均值。