与管道流动类似,当边界层流动的雷诺数Rex=Ux/υ大于某临界值时,边界层内的流动发生转捩,由层流转变成湍流。可以像推导层流边界层方程(8.27)一样推导出湍流边界层时均参数的微分方程,但是在时均湍流边界层方程中不仅有分子粘性应力项,还会出现湍流应力项。由于目前还无法建立湍流应力与时均速度之间的解析关系,因此湍流边界层方程是不封闭的。为了使方程封闭,必须选用一定的湍流模式,给出湍流应力与时均参数之间的关系式。 目前最常用的湍流模式是基于涡团粘度假设的代数方程模式、k-方程模式和k-ε方程模式。在第一种模式中,将混合长用一个代数方程描述;在第二种模式中,除了给定混合长的代数方程外还要加上一个代表湍流动能k保持平衡的偏微分方程,并将它们与时均速度方程联立求解;在第三种模式中,除了给定混合长与湍流动能方程外还要再加上一个表示湍动能耗散ε保持平衡的偏微分方程,并将它们与时均速度方程联立求解。不管采用哪一种模式,所涉及的方程组都十分复杂,除了个别极简单的情况外,一般都只可能用数值方法求解。对于这些,本书不做详细讨论,下面仍运用动量积分方程对湍流边界层求近似解。
1.湍流边界层的近似计算
前面已推导了边界层动量积分方程(8.34)
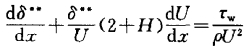

只要使用适合于湍流的时均速度分布函数,动量积分方程对湍流边界层仍然适用。对于光滑平板湍流边界层的实验研究表明,与光滑圆管内的湍流流动相比,湍流边界层流动具有类似的分层结构,也可分为粘性底层、过渡区和湍流核心区。实验还表明,在粘性底层和湍流核心区内,时均速度的变化规律与圆管湍流中的相应区域类似,因此可以把湍流水力光滑管的速度分布表达式用于光滑平板湍流边界层流动。

从第4章已经知道,水力光滑管中湍流核心区的速度分布为对数表达式(4.23),即式(8.36)所描述的速度分布在很宽的雷诺数范围内都与对数函数非常接近。当雷诺数非常大时,上式中的指数需要做调整。现在把式(8.36)给出的速度分布移植用于光滑平板湍流边界层的求解。
在边界层外缘y=δ处应该有u=U,由式(8.36)得
![]()
式(8.36)与式(8.37)相除,有



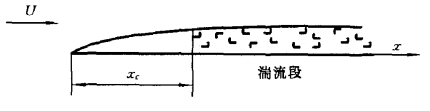
图8-11 混合边界层中的湍流段


免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















