语义编码之间的相似度计算

7．3．2　语义编码之间的相似度计算

为了进行语义编码间的语义相似度计算，必须先使《词林》中的数据能被计算机读取，且能进行数学计算，所以开始须将《词林》机读化。

先将《词林》分类体系对应的语义编码体系进行了如下描述：

例如，将“贸易”进行编码后，得到的语义编码为：He　010101，与其相对应的大类、中类、小类、小组编号分别为：（H）、（e）、（01）（01）、（01），其中：“H”表示大类“活动”，“e”表示中类“经济活动”，第一个“01”表示小类中“贸易、输出、输入、投资”，第二个“01”表示“贸易”类，最后一个“01”表示“贸易”类中第一个小组“贸易”。

为了后续计算的方便，再增加一个虚拟结点O，形成图7－2所示的树型结构^［17］。

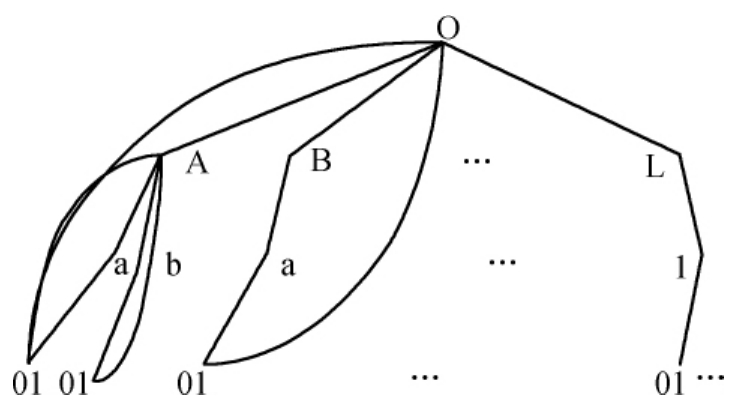
图7－2　语义距离的计算

这样“贸易”对应的编码就多了一个虚拟的字符“O”，成为“O He　010101”。

定义两语义编码（S1和S2）间的语义距离D（S1，S2）为在该树型图中从结点S1到S2的最短路径的长度。

如：D（Aa01，Ab01）＝4，D（Aa01，Ba01）＝6，D（He　010101，He　010101）＝0

语义编码S1和S2之间的语义相似度可通过公式7－1计算完成，即认为词汇间的语义相似度与语义距离成反比。

（注：若D（S₁，S₂）＝0，则令Simi（S₁，S₂）＝1）

例如，前例的计算结果如下：

Simi（Aa01，Ab01）＝1/D（Aa01，Ab01）＝1/4

Simi（Aa01，Ba01）＝1/D（Aa01，Ba01）＝1/6

Simi（He　010101，He　010101）＝1/D（He　010101，He　010101）＝1

这样便完成了语义编码间的语义相似度计算。

最后值得注意的是，由于语义编码的长度有限，可以对存在的几种相似度结果进行分类判断，这样可简便快速地得到相似度结果。

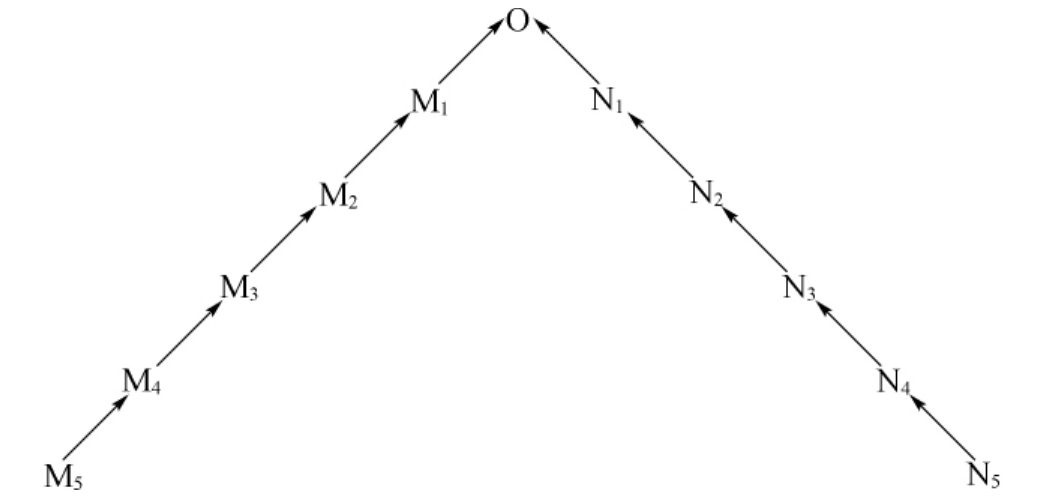
图7－3　最短路径计算原型示意图

根据图7－3，假设有两语义编码（S1：OM1M2M3M4M5和S2：ON1N2N3N4N5），可以得出《词林》语义树上任何两结点之间的最短路径D（S1，S2）。归纳如下：

①当M1≠N1，即当结点M1和结点N1不相同时，则D（S1， S2）＝10；

②当M1＝N1、M2≠N2时，D（S1，S2）＝8；

③当M1＝N1、M2＝N2、M3≠N3时，D（S1，S2）＝6；

④当M1＝N1、M2＝N2、M3＝N3、M4≠N4时，D（S1，S2）＝4；

⑤当M1＝N1、M2＝N2、M3＝N3、M4＝N4、M5≠N5时，D（S1，S2）＝2；

⑥当OM1M2M3M4M5＝ON1N2N3N4N5时，D（S1，S2）＝0；

⑦另外，考虑到《词林》大类之间的相关性，如第一至第四大类多为名词，第六至第十大类多为动词等，本系统中将不满足前六个条件，但同属于A、B、C、D大类或者同属于F、G、H、I、J大类的结点间的最短路径设定D（S1，S2）＝12；

⑧若不满足以上任何一个条件的，则其路径为：D（S1，S2）＝＋∞。

根据公式7－1，可以得到以上条件下的语义相似度，结果如下：

①当M1≠N1，Simi（S1，S2）＝1/10；

②当M1＝N1、M2≠N2时，Simi（S1，S2）＝1/8；

③当M1＝N1、M2＝N2、M3≠N3时，Simi（S1，S2）＝1/6；

④当M1＝N1、M2＝N2、M3＝N3、M4≠N4时，Simi（S1，S2）＝1/4；

⑤当M1＝N1、M2＝N2、M3＝N3、M4＝N4、M5≠N5时，Simi（S1，S2）＝1/2；

⑥当OM1M2M3M4M5＝ON1N2N3N4N5时，Simi（S1，S2）＝1；

⑦若不满足以上任何一个条件，但有M1∈｛A、B、C、D｝且N1∈｛A、B、C、D｝，或者M1∈｛F、G、H、I、J｝且N1∈｛F、G、H、I、J｝，Simi（S1，S2）＝1/12；

⑧若不满足以上任何一个条件，则Simi（S1，S2）＝0。