计算机思维的大基础

尽管人脑的思维模式极为精巧，我们仍可通过软件对人脑进行模拟。要想做到这一点，计算机必须具备准确的沟通、记忆和计算能力，具有计算的通用性和冯·诺依曼结构，并且能够按大脑核心算法进行创造性思维。

我们的大脑外在形态好似一块法国乡村面包，内在像是一个拥挤的化学实验室，充斥着无间断的神经元对话。可以把大脑想象成一堆发光的存在；一个鼠灰色的细胞“议会”；一个梦工厂；一个住在球状头骨内的小小君王；一团杂乱的神经细胞，微小但无处不在，导演着一切人生戏剧；一个变幻无常的乐园；或是一个名叫“头骨”的“衣橱”里塞满了各式各样名叫“自我”的“行头”，挤得皱皱巴巴的，仿佛小小的运动随身包里装了太多衣服。

戴安·艾克曼

大脑会存在是因为为了维持生存必须对资源进行分配，而且随着空间和时间的变化，威胁生存的因素也在不断变化。

约翰·奥尔曼

现代大脑地图给人一种有趣的古旧感——就像一张中世纪的地图，已知世界被散布着不知名怪兽的未知之地环绕。

大卫·班布里基

在数学中你并没有理解什么东西，你只是习惯了它们而已。

约翰·冯·诺依曼

自从20世纪中期电脑出现以来，关于电脑的能力极限，以及人脑能否被视为一种形式的电脑的争论就没有间断过。对于后一个问题，舆论共识已经发生转变，从认为这两种信息处理实体在本质上是相同的，转变为认为两者存在本质上的不同。那么大脑是否可被视为电脑呢？

20世纪40年代，电脑开始成为时髦的话题，它们被视为思考机器。1946年，世界上第一台电子数字积分计算机ENIAC发布，它被媒体称为“巨脑”。随着电脑在接下来的几十年里走入大众市场，广告常常称其为普通人脑无法企及的、拥有超能力的“大脑”（见图8—1）。

图8—1　1957年的一则广告，寓意电脑是一个巨型的大脑

程序使电脑名副其实。由卡内基·梅伦大学的赫伯特·西蒙（Herbert A.Simon）、J.C.肖（J.C.Shaw）和艾伦·纽厄尔（Allen Newell）发明的“通用问题解算机”，成功证明了数学家伯特兰·罗素（Bertrand Russell）和阿尔弗雷德·诺斯·怀特海（Alfred North Whitehead）在他们1913年出版的名著《数学原理》（Principia Mathematica）中无法论证的定理。在接下来的几十年里，电脑在解决数学问题、诊断疾病、下国际象棋等智力运动方面凸显出大大超越人脑的优势，但在控制机器人系鞋带，或是学习5岁大儿童就能理解的常用语言方面却困难重重，计算机现在才刚刚能够掌握这些技能。具有讽刺意味的是，电脑的进化与人类智能的成熟方向正好相反。

关于电脑和人脑在某种程度上是否等同的问题至今仍存在争议。在序言中我提到关于人脑的复杂性可以查到无数种引证。同样，在google上搜索“大脑不等同于电脑的引证”，也可以得到上百万条链接结果。在我看来，这些链接的内容都无异于在说“苹果酱不是苹果”。从技术上来说这种说法没有错，但苹果可以做出苹果酱。类似于“电脑不是文字处理器”之类的说法可能更加贴切一些。尽管电脑和文字处理器存在于不同的概念层面是事实，但是电脑在运行文字处理软件时就变成了文字处理器，反过来则不然。同样，电脑如果运行“大脑软件”则可以变成人脑。这正是很多研究人员，包括我自己正在尝试的事情。

那么问题就变成了我们是否可以找到一种算法使电脑变成等同于人脑的存在。由于具有内在通用性（仅受容量大小制约），一台电脑可以运行我们定义的各种算法，人脑却只能运行一套特定的算法。尽管人脑的模式相当精巧，不仅有极大的可塑性，还可以在自身经验的基础上重建连接，但这些功能我们可以通过软件进行仿真。

基础1：准确的沟通、记忆和计算能力

计算的通用性的理念（即一台普通目的的电脑可以植入各种算法）在第一台机器产生时就出现了。计算的通用性和可能性及对人类思维的适用性包含4个核心概念，它们很值得探讨，因为人脑也在对其进行运用。第一个是准确的沟通、记忆和计算能力。在1940年，如果你使用“计算”这个词，人们会认为你在说模拟电脑。模拟电脑的数字由不同程度的电压代表，而且特定的模块可以运行加、乘等运算。然而，模拟电脑的一个很大的限制是准确性存在问题。其准确性只能达到小数点后两位数，而且随着处理代表不同数字的电压的操作员增加，错误也随之增多。所以无法进行较大量的计算，因为结果会由于准确性太低而失去意义。

只要曾用模拟磁带机录制过音乐的人都会知道这一效应。第一遍拷贝的质量会打折，相比原版听起来有较多杂音（此处的“杂音”代表随机错误）。把第一遍拷贝再进行拷贝会出现更多杂音，到第十遍的拷贝时，基本上就只剩下杂音了。数字计算机的崛起伴随着同样的问题，思考一下数字信息的沟通通道我们就可以理解了。没有任何通道是完美的，通道本身都存在一定的错误率。假设一条通道有90%的可能性能正确传送每个比特的信息。如果我传送的信息有1比特，那这条通道正确传送它的可能性为0.9，假如我传送2比特信息呢？那准确率就变成了0.92＝0.81。假如我传送1字节（8比特）信息呢？那我准确传送该信息的可能概率连50%都达不到（准确地说是0.43）。准确传送5字节信息的可能性仅为1%。

解决这个问题的一个方法就是增加通道的准确性。假设一个通道在传送一百万比特时出现一个错误，如果我传送的文件包含50万字节（约为一个普通的程序或数据库的大小），尽管通道固有的准确性较高，但正确传送它的可能性仍不到2%，而单单一个比特的错误就可以彻底毁掉整个程序或其他形式的电子数据，所以这种情形并不能令人满意。除了通道的准确性，另一个棘手的问题是传送中出现错误的可能性随着信息量的增加而迅速增加。

模拟计算机通过柔性降级的方法处理该问题（即用户只用其处理能容忍出现一些小错误的问题）。如果用户能将其运用限制于一定的计算，那么模拟计算机确实是有用的。然而数字化计算机要求连续的通信，不仅是在不同的计算机之间，也包括计算机自身内部：从内存到中央处理器之间存在通信；在中央处理器中，不同寄存器和算法单元之间也在进行通信；在算法单元内，从一个比特寄存器到另一个之间也在进行交换。通信在每个层次上都普遍存在。如果错误率随着通信的增多快速增加，而一个比特的错误就可以破坏整个过程的完整性，那么数字化计算注定会失败，至少在当时看来是这样的。

引人注目的是，这种普遍的认识在美国数学家克劳德·香农（Claude Shannon）出现并展示了怎样通过最不可靠的沟通通道来进行精度很高的通信时得以改变。1948年7月和10月，香农在《贝尔系统技术杂志》（Bell System Technical Journal）上发表了具有里程碑意义的论文《通信的数学原理》（A Mathematical Theoryo of Communication），提出噪声通道编码理论。他认为无论通道的错误率是多少（除了错误率正好为每比特50%的通道，因为这意味着该通道传输的是纯粹的噪声），都可以按想要的精度传送信息。换句话说，传输的错误率可以是n比特分之一，但是n的大小可以随意定义。比如说，在端限情况下，就算一个通道的正确率仅为51%（即该通道传送的正确信息的比特数仅比错误信息的比特数多一点儿），仍然可以使传输的信息错误率达到百万分之一，甚至万亿分之一，甚至更小。

这是怎么做到的呢？秘诀就在于冗余。这在现在看来似乎是显而易见的，但在当时则不然。举一个简单的例子，假如我每比特信息都传送3次，并且选传输后多数相同的那条信息，那么我就可以大大地提高信息的可靠性。不断增加冗余就能让你得到你需要的精度。不断重复传送信息是从准确性较低的通道得到任意高精度信息最简单的方法，但不是最有效率的方法。香农的论文开创了信息理论这一领域，为错误侦查和校正码提供了最理想的方法，使在任意非随机通道条件下获得任意目标精度成为可能。

年纪较大的读者可以回想一下电话调制解调器，它通过嘈杂的模拟电话线路传递信息。幸好有了香农的噪声通道理论，尽管这些线路存在可以听到的明显的嘶嘶声、砰砰声或其他形式的声音失真，它们仍然可以传送高精度的数字化信息。数字存储器也存在同样的问题和解决办法。你是否想过为什么就算唱片曾掉在地上并且有刮痕，CD、DVD或其他磁盘软件仍能准确地读出音乐吗？这也多亏了香农。

计算包含3个部分：通信（正如我之前提到的，在计算机内部和计算机之间普遍存在）、存储器和逻辑门（可进行计算和逻辑功能）。逻辑门的准确性可以通过错误侦查和校正码达到任意高的精度。幸好有了香农的理论，不管多大多复杂的数字化信息和算法，我们都可以准确处理，避免过程中出现较高的错误率。需要指出的很重要的一点是，我们的大脑也在运用香农的理论。当然，人脑的进化远远先于香农发现这一原理。绝大部分模式或思想（思想也是一种模式）在大脑中储存时都包含大量的冗余。冗余出现的首要原因是神经传输系统自身的不可靠性。

基础2：计算的通用性

第二个信息时代所依赖的重要思想是我之前提到过的：计算的通用性。1936年，阿兰·图灵提出“图灵机”（见图8—2），但它并非真实存在，仅仅是一种假想的机器。他的假想计算机包含无限长的记忆磁带，每个平方上有一个1或0。输入呈现在记忆磁带上，机器每次可以读出一个平方。这台机器还包含一个规则表（核心是一个记忆程序），是由数字编码的各种状态组成的。如果被读出的平方上的数字为0，每条规则指定一个行动，如果为1则指定另一个行动。可能的行动包括在记忆磁带上写0或1，将记忆磁带向右或向左移动一个平方，或者停止。每条状态都会指定机器应该读取的下一条状态的数字。

“图灵机”的输入呈现在记忆磁带上。程序不断运行，当机器停止工作时，它已完成了算法，并且将过程输出在记忆磁带上。请注意，虽然磁带的长度在理论上是无限的，但实际的程序如果不进入无限循环的话只会用掉有限长的磁带，所以假如我们只去看那部分有限的磁带，就可以解决一类有用的问题。

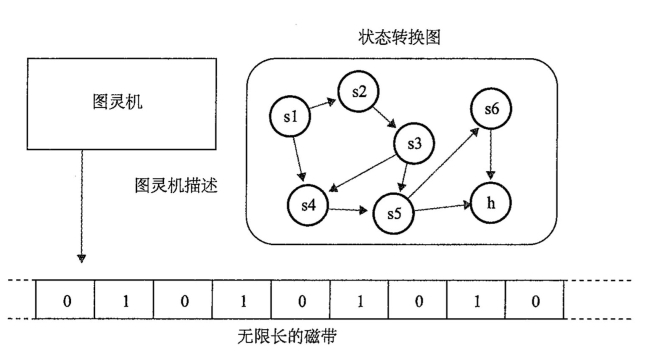
图8—2　无限的记忆磁带

注：图灵机的框图，带一个能读写磁带的前端，还有一个由状态转换组成的内置程序。

如果你认为“图灵机”听上去很简单，那是因为这正是发明者的目的所在，图灵希望他的机器尽可能简单（但不是简化，引用爱因斯坦的说法）。图灵和他的前教授阿隆佐·邱奇（Alonzo Church）接着开发了邱奇—图灵论，称如果一个问题无法利用图灵机解决，那根据自然定律，任何其他机器也解决不了。尽管图灵机只有少数命令，并且每次只能处理1比特，但它能完成任何其他计算机能完成的计算。换一种说法就是“图灵完全”（即拥有与图灵机同等能力）的机器能够完成任何算法，即任何我们能定义的程序。

邱奇—图灵论的一种强有力的诠释在本质上将人的思想或认知与机器的计算等同起来，其基本论点是人脑同样遵循自然定律，因此它的信息处理能力不可能超过机器，即图灵机。

我们可以将图灵发表于1936年的论文视为计算理论的基础，但同时也应注意到他深受匈牙利裔美国数学家约翰·冯·诺依曼的影响。冯·诺依曼1935年于剑桥讲授他的存储程序概念，这一概念在图灵机中得到深刻的体现。反过来，冯·诺依曼也受到图灵发表于1936年的论文的影响，该论文提出了计算的原则，在20世纪30年代末和40年代初成为同行必读论文一。

在该论文中，图灵提出了另一个意想不到的发现：无法解决的问题，它们由唯一的答案定义，并且答案是存在的，但我们可以证明它们无法通过任何图灵机进行计算，即无法通过任何机器计算。这与19世纪的认识——只要问题能被定义，那么最终就能被解决——正好相反。图灵向我们展示了无法解决的问题和可以解决的问题一样多。澳大利亚裔美国数学家和哲学家库尔特·哥德尔（Kurt Gödel）在他1931年提出的“不完全定理”中提出了类似的结论。我们因此面临一个令人困惑的情形，即我们可以定义一个问题，也可以证明唯一的答案存在，但却永远得不到答案。

图灵展示了在本质上，计算是基于一个非常简单的机制。因为图灵机（包括任何计算机）能够将它未来的行动进程建立在已经计算出的结果之上，因此它能够进行决策并对任何复杂的信息层级进行建模。

1939年，图灵设计了一个叫作“炸弹”的电子计算器，帮助破译了纳粹“谜”式密码机编写的情报。1943年，一个受图灵影响的工程师小组发明了“巨像”计算机，这可以说是世界上第一台电脑，它帮助同盟国解码了更复杂的“谜”式密码机编写的情报。“炸弹”和“巨像”是针对某一个任务设计的，并且不能被重新编程用于解决其他任务，但是它们都出色地完成了自己的使命，帮助同盟国克服了纳粹德国空军相对于英国皇家空军的三比一的优势，并对纳粹可能采取的战术进行预测，使英国获得了关键战役的胜利。

基础3：冯·诺依曼结构

在前文所述基础之上，约翰·冯·诺依曼设计了现代计算机的构造，这引出了我的第三个主要思想：被称作“冯·诺依曼机”的结构构成了过去67年里每台计算机实质上的核心结构，从你家洗衣机里的微型控制器到最大型的超级计算机，无一例外。在写于1945年6月30日，题目叫做《关于电子数据计算机报告的第一次草案》（First Draft of A Report on The EDVAC）的论文中，冯·诺依曼提出了自此以后主导计算领域的理论，即冯·诺依曼模型——包括一个进行计算和逻辑运算的中央处理器，一个存储程序和数据的内存单元，一个大容量存储器，一个程序计数器，以及输出/输入通道。尽管这篇论文的本意是作为内部项目文件，但它实际上已成为计算机设计师的“圣经”。你永远也想不到一个看似普通的日常内部备忘录也许会在某一天改变整个世界。

图灵机并不是为了实用而设计的。图灵的定理并不着重于解决问题，而在于检视理论上能通过计算解决的问题的边界。冯·诺依曼的目的是提出一个计算机器的可行性模型。他的模型用多比特语言代替了图灵的单比特计算（通常是8比特的倍数）。图灵的记忆磁带是连续的，所以图灵机的程序在存储和提取结果时需要花费大量时间来回倒带或进带。相较之下，冯·诺依曼的存储器是随机存取的，所以任何数据都可以立刻被提取出。

冯·诺依曼的一个核心观点是他10年前引入的关于存储程序的：将程序像数据一样放在同样类型的随机存取存储器中（通常放在同样的内存区块中），就可以使计算机通过重新编程来应对不同的任务，同时进行代码的自我修改（假如记忆程序可写的话），从而实现一种强大的递归形式。在那之前，所有的电脑，包括“巨像”，都是设计来解决一种任务的。存储程序使计算机通用化成为可能，从而实现图灵关于通用计算的设想。

冯·诺依曼机的另一个关键方面在于各个指令都包含一个指定要进行的算术或逻辑运算的操作代码和一个指向内存中的操作数的地址。

冯·诺依曼关于计算机架构的理念是通过他设计的电子数据计算机（EDVAC）的问世为人所知的。EDVAC是他和J.普雷斯伯·埃克特（J.Presper Eckert）、约翰·莫克利（John Mauchly）合作的项目。EDVAC直到1951年才开始真正运行，当时还出现了其他存储程序计算机，比如曼彻斯特小规模实验机，电子数字积分计算机（ENIAC），电子延时储存自动计算机（EDSAC），二进制自动计算机（BINAC），它们都多多少少受到冯·诺依曼论文的影响，而且埃克特和莫克利都参与了设计。所有这些机器的产生，包括ENIAC之后推出的支持存储程序的版本，冯·诺依曼都是当之无愧的直接贡献者。

冯·诺依曼机问世之前还出现过几位先导，但它们中没有一个是真正的冯·诺依曼机。1944年霍华德·艾肯推出了马克一代，它有可编程的元素但不使用存储程序。它从一个穿孔的纸带上读取指令，然后立刻执行各项命令，但缺乏条件分支指令。

1941年德国科学家康拉德·楚泽（Konrad Zuse）创造了Z-3计算机。它也是从一个记忆磁带（用的是胶卷）上读取程序，没有条件分支指令。有趣的是，楚泽得到德国飞行器研究机构的支持，该机构用楚泽的设备来研究机翼的摆动，但楚泽向纳粹政府提出的用真空管更换继电器的资金支持申请却遭到了拒绝，因为纳粹政府认为研究计算对战争来说不那么重要。在我看来，纳粹战败的结果几乎可以用这种错误观点的长期存在来解释。

但冯·诺依曼的理念有一位真正的先驱，并且可以追溯到整整一个世纪之前！他就是英国数学家和发明家查尔斯·巴贝奇（Charles Babbage）。1837年，巴贝奇首次描述了一种名为分析机的机器，该机器就体现了冯·诺依曼的理念，其特点是用穿孔卡片作为存储程序，灵感来自于雅卡尔织布机。它的随机存取存储器包含1000个字，每个字由50个十进位数组成（等同于约21个千字节）。它的各个指令包含一个操作码和一个操作数，就像现代机器语言。它还包含条件分支和循环，所以是货真价实的冯·诺依曼机。它完全基于机械齿轮。分析机似乎超出了巴贝奇的设计和组织技能，他制造出了各个部件但并没有真正让它运行起来。但我们不清楚包括冯·诺依曼在内的20世纪的计算机鼻祖们是否对巴贝奇的工作有所了解。

巴贝奇的计算机实际上导致了软件编程领域的产生。英国作家艾达·拜伦（Ada Byron）——勒芙蕾丝伯爵夫人，诗人罗德·拜伦的唯一合法继承人可以说是世界上第一个计算机程序设计员。她为分析机编写了程序，即今天软件工程师所熟知的“查表法”。不过，她只需要在自己的脑子里进行调试（因为计算机从没有真正工作过）。她翻译了意大利数学家路易吉·梅约布雷亚（LuigiMenabrea）关于分析机的文章并加上大量自己的注释。她写道：“分析机编织代数的模式如同雅卡尔织布机编织出花朵和叶子的花纹一样。”她接着提出了可能是世界上第一个关于人工智能可能性的推断，又总结说分析机“不能自命不凡，认为什么问题都能解决”。

巴贝奇能在他生活和工作的时代提出如此先进的理念不能不令人称奇，但直到20世纪中期他的思想才得到人们的重视。是冯·诺依曼使我们今天所熟知的计算机原则概念化和清晰化，而且冯·诺依曼机作为计算的最重要模型在全世界得到普遍认可。但要记住的是，冯·诺依曼机在各种单元之间和单元内部持续地进行数据通信，因此它的实现多亏了香农提出的对数字化信息进行可靠传输和存储的理论。

基础4：按大脑核心算法进行创造性思考

这引出了我们的第四个重要的思想，即打破艾达·拜伦提出的计算机不能进行创造性思考的结论，探索大脑采用的核心算法，将电脑变成人脑。阿兰·图灵在他1950年的论文《计算机器和智能》（Computing Machinery and Intelligence）中提出这个目标，还设计了今天有名的图灵测试来确认某一人工智能是否能达到人类的智力水平。

1956年，冯·诺依曼开始为耶鲁大学享有声望的西里曼讲座系列准备讲演。但由于癌症的折磨，他没有机会真正登上讲台，也没有完成手稿。但这些未完成的手稿仍然对计算机的发展——在我看来是人类最令人却步又最为重要的工程，作出了精彩而有预见性的构想，并于1958年作者去世后出版，名为《计算机与人脑》（The Computer and The Brain）。20世纪最杰出的数学家和电脑时代的先驱的最后著作是对智能的检视，这真是再合适不过了。这部作品是最早从数学家和计算机科学家的角度对人脑进行的严肃探究。在冯·诺依曼之前，计算机科学和神经科学是没有任何交集的两个领域。

冯·诺依曼应用计算通用性的概念得到的结论是：尽管人脑和计算机的结构截然不同，但仍可以认为冯·诺依曼机能够模仿人脑对信息的加工过程。反之则不然，因为人脑不是冯·诺依曼机，而且没有同样的存储程序（尽管我们的大脑可以模拟一个非常简单的图灵机的工作过程），它的运算法则或方式是内隐于结构中的。冯·诺依曼正确地归纳了神经可以从输入中学习模式，这些模式现在已被确定，并且部分通过树突强度来编码。在冯·诺依曼的时代还不为人所知的是，学习同样通过神经元连接的建立和破坏来进行。

冯·诺依曼有预见性地指出神经加工的速度极为缓慢，大约每秒能进行100次计算，但是大脑通过大量的并行处理来补偿速度——这是他的又一个重要的洞察。冯·诺依曼认为大脑的1010个神经在同时工作（这个估计值相当准确，今天估计的数目在1010到1011之间）。实际上，每个连接（每个神经平均有约103到104个连接）也都在同时进行计算。

考虑到当时神经科学的发展还处于初始阶段，冯·诺依曼对神经加工过程的推测和描述工作称得上是非常杰出。但他对大脑记忆容量的推测我却无法苟同。他称大脑能记住人一生中所有的输入。他认为人的平均寿命为60年，即2×109秒。每秒每个神经约有14个输入（这比实际情况低了至少3个数量级），神经总数为1010个，那么可推断大脑总的记忆容量约为1020比特。但正如我之前提到的，事实上我们只能记住我们的思想和经历的一小部分，而且这些记忆的存储模式不是处于较低水平的比特模式（像视频图像一样），而是处于较高水平的序列模式。

冯·诺依曼在提出大脑工作的各个机制的同时，也展示了现代计算机怎样完成跟大脑同样的工作。尽管两者有明显的差异，但是大脑的模拟机制可以被数字化仿真，因为数字化计算可以实现任意精度的对模拟值的仿真（而且大脑内的模拟信息精度非常低）。考虑到计算机在连续计算中显著的速度优势，大脑中的大规模平行工作构造同样可以被仿真。另外，我们也可以通过平行地使用冯·诺依曼机在计算机上实现并行处理——这正是今天的超级计算机工作的原理。

冯·诺依曼推断说大脑的工作方式不能包含较长的连续算法，否则人在如此慢的神经计算速度下无法快速作出决定。当三垒手拿到球并且决定扔到一垒而不是二垒时，他是在不到一秒的时间内作出这个决定的，这段时间仅够各个神经进行少数几轮循环。冯·诺依曼正确推断了大脑的出色能力来自于一千亿个细胞可以同时处理信息，因此视觉皮质只需要3到4个神经循环就能作出复杂的视觉判断。

大脑极大的可塑性使我们能够进行学习。但计算机的可塑性更大，通过改变软件就可以完全重建它的工作方式。因此，从这点上看，计算机可以仿真大脑，但反过来则不然。

冯·诺依曼在他的时代将进行大量平行计算的大脑的容量与计算机进行了对比，得出大脑有更强大的记忆力和速度的结论。现在能够在功能上仿真人脑（每秒运行约1016次），在某些方面能达到保守估计的人脑速度的第一代超级计算机已经出现。（我预测这种水平的计算机在21世纪20年代初期的费用将为1000美元左右。）在记忆容量方面，计算机和人脑就更接近了。虽然在他写作手稿的时候计算机还处于发展的初始时期，但冯·诺依曼已充满信心地认为人类智能的“硬件”和“软件”之谜最终会被解开，这也正是他准备这些演讲的动机所在。

冯·诺依曼深刻地意识到科技发展不断加快的脚步及其对人类未来的深远意义。在1957年他去世一年后，他的同事数学家斯坦·乌拉姆（Stan Ulam）引用他在20世纪50年代早期说过的话：“技术的加速发展和对人类生活模式的改变的进程在朝向人类历史上某种类似奇点的方向发展，在这个奇点之后，我们现在熟知的社会作用将不复存在。”这是人类技术史上第一次使用“奇点”这个词。

冯·诺依曼的基本见解是电脑和人脑在本质上等同。请注意，生物人的情商也是它智能的一部分。如果冯·诺依曼的见解是正确的，并且假如你能接受这个信念的飞跃，即令人信服地重现了生物人的智能（包括情感等其他方面）的非生物实体是有意识的，那么我们能得到的结论就是电脑（安装了恰当的软件）和人类意识本质上是可以等同的。那么，冯·诺依曼是正确的吗？

今天绝大多数的电脑是完全数字化的，而人类大脑结合了数字法和模拟法。模拟法由数字法进行再现，再现较为容易且程序化，并能达到任意想要的精度。美国计算机科学家卡弗·米德（Carver Mead）提出了可以用他命名为“神经形态”的硅制芯片直接仿真人脑的模拟法，这种方法比数字仿真模拟法的效率高上千倍。因为我们对新皮质大量重复的算法进行了编纂，所以完全可以使用米德的方法。由达曼德拉·莫德哈（Dharmendra Modha）领导的IBM认知计算小组已经推出了能够仿真神经和神经连接，并且能形成新连接的芯片，将之命名为“突触”。它的其中一个芯片能直接仿真256个神经和约25万个突触连接。这个项目的目的是创造一个非常接近人类大脑的，功率仅为1千瓦的，拥有100亿神经和100万亿神经连接的仿真真皮质。

正如冯·诺依曼在半个世纪之前描述的那样，大脑运行速度极其缓慢却拥有大量的平行运行线路。今天的数字电路至少比大脑的电化学交换快1000万倍。不过，大脑真皮质的3亿个模式识别器同时运行着，神经元间的上百亿个连接也同时进行着计算。提供能成功模拟人脑的必要硬件的关键问题在于实现总的记忆容量和计算量，而不是直接复制大脑的结构，但这种做法非常缺乏效率和灵活性。

让我们判断一下这些硬件要满足哪些要求。许多工程试图模拟在新皮质发生的分层学习和认知模式，包括我自己在进行的关于隐马尔可夫层级模型的研究。根据我自己的经验作出的保守估计是，模拟生物大脑新皮质上的一个模式识别器的一次循环需要约3000次计算。绝大部分仿真运行的次数达不到这个估计数。大脑每秒进行约102（100）次循环，那么每秒每个模式识别器会达到3×105（300000）次计算。假设按我的估计模式识别器的数目在3×108（3亿）左右，我们可以得到每秒1014（100万亿）次计算，这个数目与我在《奇点临近》中的估算是一致的。在那本书中我推断为了在功能上仿真大脑需要每秒进行1014到1016次计算，而1016次每秒只是保守估计。人工智能专家汉斯·莫拉维克（Hans Moravec）根据整个大脑内初始视力加工过程所需要的计算量推测得出的数字为1014次每秒，这与我的估计是一致的。

常规台式计算机可以达到1010次每秒，但这个速度可以通过云资源得到极大的提升。最快的超级计算机，日本的计算机K的速度已经达到了1016次每秒。考虑到新皮质的算法大都是重复进行的，使用“神经形态”芯片的方法，例如上文中提到的IBM的“突触”的前景非常乐观。

在记忆容量的要求方面，我们需要约30比特（约4字节）来使一个连接响应3亿个模式识别器中的一个。如果我们估计每个模式识别器向上平均有8个输入，即每个识别器收到32字节输入。如果我们给每个输入多加1字节，那么就有40字节。加上向下连接的32字节，总共就有72字节。但连接上下层级的分支通常会远远多于8个输入。请注意，较大的分支树通常由多个识别器共享，比如，可能会有上百个识别器参与识别字母“p”，那么在更高一层，即识别包含“p”的单词或词组的层级就会有更多的、成千上万个识别器参与。然而，各个较低层级的“p”识别器并不分别占有连接高一层级的分支树，而是共享同一个连接分支树。对于向下的连接也是同样的道理：一个负责单词“APPLE”的识别器会通知所有低一层级的负责字母“E”的识别器，如果它看到了“A”、“P”、“P”、“L”那么就有可能会出现“E”。对于需要向低一层级通知“E”可能会出现的各个单词或词组识别器而言，连接树并不是多个重叠的，而是共享同一个。因为这个原因，总体上估计平均每个识别器上下各8个输入是合理的。即使增加个别识别器的估计数，也不会显著影响估计结果的数量级。

3×108（3亿）个模式识别器各有72字节输入，那么加起来总共就可以得到2×1010（200亿）字节的记忆容量。这对于今天的常规计算机来说算不上一个太大的数字。

以上这些估算主要是为了提供一个大致的数量级估计。考虑到数字电路的速度是新皮质的生物性电路的1000万倍，我们就不需要在平行构造的规模方面向人脑看齐，一般规模的平行构造就足够了（人脑中的平行线路高达万亿级）。我们可以看到计算方面的必要要求都已经能够达到了。大脑的重新连接——树突持续不断地产生新的突触，也可以通过运用连接的软件来仿真，这个仿真系统比大脑还要灵活得多，相比之下大脑存在较多局限。

大脑用于保持记忆稳定性和一致性的冗余也完全可以用软件模拟。优化这类自组织层级学习系统的数学方法已经被充分理解。但大脑的组织还远远达不到优化的水平，当然，它也不需要达到最优化，只需要达到能够制造工具弥补自身水平的不足就足够了。

人类新皮质的另一个限制在于没有排除或复查相互矛盾的思想的程序，这导致很多时候人们的思想缺乏一致性。我们也缺乏一个强有力的机制来执行批判性思想，当我们需要这个技能的时候，几乎一半的情况下都没能有效运用。一个以软件为基础的新皮质可以通过建立一个暴露不一致性的程序来克服这个弱点，方便我们对自身思想进行复查。

值得注意的是，设计整个大脑区域反而比设计单个神经元要简单。正如我们之前讨论的，用计算机进行模拟，越高层级的模型反而越简单。为了模拟晶体管，我们需要理解半导体的物理特性的细节，而且一个真正的晶体管即使只是基础方程也非常复杂。一个能将两个数字相乘的数字电路需要上百个晶体管，但我们通过一两个公式就能准确模拟这个乘法电路。一个包含上十亿个晶体管的电脑的模拟仅需要指令系统和注册描述，短短几页文本和公式就能包括全部内容。操作系统、语言编译器或汇编程序的软件程序则相对复杂，但是模拟一个特定程序——比如一个基于隐马尔可夫层级模型的语言识别程序则可以通过短短几页方程完整描述。在这些描述中肯定不会出现半导体物理特性的细节或电脑的构造。

类似的现象对大脑也同样适用。新皮质上侦查某一不变的视觉特征（比如人脸），或是执行声音的带通滤波（将输入限定在一个特定的频率范围内）任务，或是评价两个事件时间接近性的模式识别器，与控制神经递质、粒子通道，以及参与神经过程的其他突触或树突变异的化学物理联系相比，能得到的细节更少。尽管在迈向更高的概念层面之前需要仔细考虑所有这些复杂性，但绝大部分可以被简化，就像大脑展现的工作方式一样。