爱因斯坦的相对性和牛顿的相对性之间的主要差别是，把相对运动着的坐标系之间的坐标和时间联系在一起的变换规律不一样。正确的变化定律，即洛伦兹变换是
这些方程对应于这样一种较为简单的情形，即两个观察者的相对运动是沿着他们的公共的x轴进行的。别的运动方向当然也是可能的，但是，最普遍的洛伦兹变换是相当复杂的，其中全部4个变量都混合在一起。我们将继续使用这种比较简单的形式，因为它包含了相对论的所有基本性质。
下面我们来讨论这个变换的更多的推论。首先，反解出这些方程是有意思的。更确切地说，这是一组线性方程组，4个方程有4个未知数，它们可以被反解出来，用x'，y'，z'，i'来表示x,y，z,i。结果非常有趣，因为它告诉我们，从一个“运动着”的坐标系上看，一个“处于静止”的坐标系是怎样的。当然，由于运动是相对的和匀速的，因此，“在运动”的那个人，如果他愿意的话，也可以认为，在运动的实际上是另一个人，而处于静止的是他自己。又由于这另一个人朝相反的方向运动，因此，他就应该得到相同的变换，但是速度的正负号要反过来。这正好就是我们通过数学推导得出的结果，因此，两者是一致的。如果得出的结果不是这样的话，那么，我们倒真的有理由要担忧了！
接下来我们讨论相对论中速度的合成这样一个有趣的问题。我们想到原先的一个难解之谜，光在所有参考系中都以186000英里/秒（1英里约为1.609千米）传播，即使这些参考系在做相对运动也是如此。以下要讲到的例子说明，这是更普遍的问题中的一个特殊的情形。设想在一艘宇宙飞船中有一个物体正以100000英里/秒的速度运动，而宇宙飞船本身则正以100000英里/秒飞行；在一个外部的观察者看来，宇宙飞船中的这个物体运动得有多快呢？我们也许应该说200000英里/秒，这比光速还快。这非常令人沮丧，因为不能想象物体会跑得比光还快！下面来讲普遍的问题。
我们假设，对飞船里的人来说，飞船内的物体正以速度v运动，而宇宙飞船本身相对于地面具有速度u。我们想知道，在地面上的人看来，这个物体以多大的速度vx运动。这当然也还是一个运动沿着x方向进行的特殊情形。还有一个沿y方向的或者沿任意方向的速度的变换；这些都可以在需要时推导出来。在宇宙飞船内，速度是vx'，这表示位移x'等于速度乘时间：
我们现在只需要算出，在外部观察者看来，一个x'和i'之间满足关系式（4.3）的物体的位置和时间。这样，只要简单地把式（4.3）代入式（4.2）中就得到
可是我们随即看到，x是用i'表示出来的。为了得出飞船外的人所看到的速度，我们必须用他的时间而不是用另一个人的时间去除他的距离！因此，我们还必须算出从飞船外所看到的时间，这个时间是
我们现在必须求出x与i之比，结果是
已经把平方根消掉了。这就是我们寻找的规律：合成后的速度，即两个速度之“和”，并非正好是两个速度的代数和（我们知道不能这样，否则，我们就有麻烦了），而是被1+uv/c2“修正”了。
下面让我们来看一看到底是怎么回事。假如你在宇宙飞船中正以一半光速的速度运动，而宇宙飞船本身也是以该速度飞行。这样，u和v都是c/2，而在分母中uv却是1/4，因此
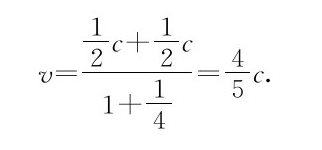
这样看来，在相对论中，“一半”加上“一半”并不等于“1”，结果只等于“4/5”。当然，低速就可以用熟悉的方法相当容易地加起来，因为只要速度与光速相比是小的，我们就可以不考虑（1+uv/c2）这个因子；但是，在高速下，事情就完全不同了，而且也相当引人入胜。
我们来考虑一种极限情形。纯粹为了好玩，假设宇航员正在宇宙飞船中观察光波本身。换句话说，v=c，而宇宙飞船还是在运动。在地面上的人看来会是怎样的呢？答案将会是
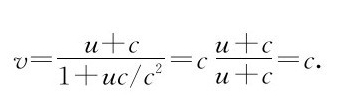
因此，如果在飞船内有什么东西正以光速运动，那么，在地面上的人看来它还是以光速运动！这很好，因为它事实上就是爱因斯坦提出相对论的本来目的——由此可见，这个理论具有较好的成效！
当然，存在这样的情形，运动并不沿着匀速平移的方向。比如说，在飞船内可能会有一个物体正好相对于飞船以速度vy'“向上”运动，而飞船则“水平地”飞行。下面，我们就来做同样的推导，只是要用y方向的量而不是x方向的量，所得的结果是
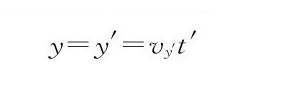
所以，如果vx'=0，就有
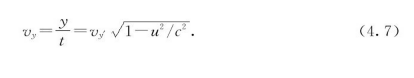
因此，横向速度不再是vy'，而是
了。我们通过将变换方程组做替换和组合而得出了这个结果，但是，由于以下的原因（再去探究一下我们是否能够明白这个原因总是好的），我们也能够直接从相对性原理看出这个结果。我们已经讨论过（图3-3）一个合理的时钟在运动时怎样工作；在静止的坐标系中看，光以速度c倾斜一个角度传播，而在运动的坐标系中看，光以同样的速度只是沿垂直方向运动。当时我们发现，在静止的坐标系中，速度的垂直分量比光速小一个因子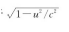
[参见方程（3.3）]。不过，现在我们假设，让一个实物粒子在这同一个“时钟”内往返运动，只是其速度是光速的某个整分数1/n（图4-1）。于是，当粒子走完了一个来回时，光正好走完n个来回。这就是说，“粒子”钟的每一次“滴答”声将与光钟的第n次“滴答”声重合。这个事实在整个系统运动时必定还是正确的，因为重合这个物理现象在任何参考系中都将是一个重合的现象。因此，由于速度cy小于光速，粒子的速度vy就必定比对应的速度小同一个平方根因子！这就是平方根之所以会出现在所有垂直速度中的原因。
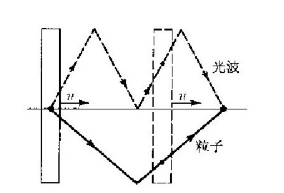
图4-1 在一个运动时钟内，一根光线和一个粒子描出的轨迹
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
