
用时:________ 正确率:________%

在接触竖式算法之前,我们先必须温习一下之前的从左至右的加法算法,从高位到低位一步步算起。事实上,竖式算法和之前接触的从左至右的加法算法有相同的地方。现在,我们就来进行一下学习和比较,看看哪个算法略胜一筹。
19+72=
第一,被加数的十位数和加数的十位数对齐相加,即为1+7=8。

第二,被加数的个位数和加数的个位数相加,即9+2=11。
第三,数字对齐相加。

答案为:91
48+76=
第一,被加数的十位数和加数的十位数对齐相加,即4+7=11。

第二,被加数的个位数和加数的个位数对齐相加,即8+6=14。

第三,将得数对齐位后相加,即:
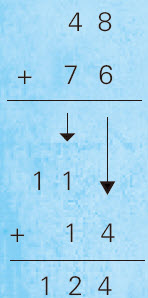
答案为:124。
239+174=
第一,将被加数的百位数和加数的百位数对齐相加,即2+1=3。

第二,将被加数的十位数和加数的十位数对齐相加,即3+7=10。

第三,将被加数的个位数和加数的个位数对齐相加,即9+4=13。

第四,将所有结果对齐相加,即:
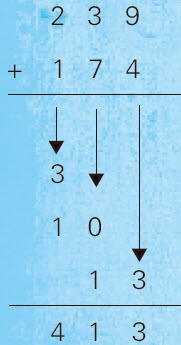
答案为:413。
竖式算法
第一步:要将数学算式写为竖式。
第二步:将被加数的各个位数的数字和加数的各个位数的数字对齐,然后开始从高位算起,如果各个位数的数字相加之和大于10,就需要进位。
第三步:将各个部分的结果相加,即为算式的最后结果。
在学习了相关的竖式算法后,我们来实践一下吧!


在印度,产生于6世纪的整数的十进制位值制记数法,其实是用9个数字和表示零的小圆圈,再借助于位值制便可表示任何数字。对于“零”,印度数学不只是把其看成空位,而是让“零”参与数学运算,这是印度数学的一大贡献。
8世纪的时候,这套数字和位值记数法传入穆斯林国家,被阿拉伯人采用并做了相关的改进。13世纪初经斐波纳契的《算盘书》流传到欧洲,逐渐演变成今天广为利用的1、2、3、4……称为印度—阿拉伯数码。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















