3.2.1 Elman网络简介
该网络因Elman J.L首先提出而得名[4],其网络结构如图3.1所示。
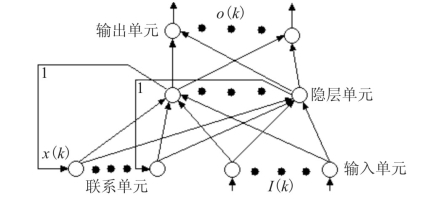
图3.1 基本Elman网络结构
其各层输入关系为:

其中,I(k)∈R r,X(k)∈R n,O(k)∈R m,W D∈R n∗n,W I∈R n∗r,W O∈R m∗n,f,g分别为输出单元和隐层单元之激发函数所组成的非线性向量函数。
特别地,当W I为对角阵时,网络具有自反馈特性,此时称之为对角回归网络。
3.2.2 Elman网络的学习算法讨论
在不同的文献中,存在基于梯度下降法的三种不同学习算法,其之所以不同,是由于反馈环节引入网络后对反馈项与权重关系的不同理解造成的,下面分别描述这三种学习算法(批处理情形)。
3.2.2.1 文献[2]的算法
设训练集为(I(k),O d(k)),实际输出为{O(k)},k=1,…,N。I(k)=(I 1(k),…,I r(k))T;O d(k)=(O d1(k),…,O dm(k))T;O(k)=(O 1(k),…,O m(k))T。定义误差指标函数为:

则按文献的推导,网络的动态算法可归纳如下:

其中,
3.2.2.2 其他两种不同的学习算法
文献[5]是一篇研究Elman网络特例——对角回归网络及其在系统辨识和控制中的重要文献。其研究结果被广为引用。在学习算法问题上,该文作者提出的算法与上述算法在(3.5)式上有歧异。具体地说,即3.1所引文献中作者认为回归项X(k-1)与W I无关,该文作者则认为X(k-1)不仅与W D有关(即支持(3.8)式),而且与W I亦存在联系。将这个结论推广到一般情形,并用统一的描述方式,则对应于(3.6)式有:

文献[6]则指出:文献[4]中的推导中“对网络权值并没有给出采样时刻”,并指出若假设第k个采样时刻网络权值为W(k),可推得:
需要指出的是:虽然文献[5]讨论的是对角回归网络,容易推广到一般的Elman网络。
3.2.2.3 对三种学习算法的评论与分析
从上面引述的三种学习算法中,我们可以清楚地看到分歧的焦点在X(k-1)与W D和W I的关系上。算法1认为X(k-1)为W D的函数而与W I无关,算法2认为X(k-1)为W D,W I的函数,而算法3认为X(k-1)与W D,W I皆无关。孰正孰误,下面我们通过各层的I/O关系来进行分析。为分析方便,重写1—3式如下:

由(3.16)式可知,一旦给定I(1),…,I(k)以及隐层输出初值X(0),X(k)的值就可由W D,W I决定。而这里k不失一般性,因此X(k-1)亦为W D,W I的函数。这里还须指出,虽然许多算法权值的递推步与采样步同步,但递推步与采样步并无实质联系,我们也可在两个采样步之间设置多个递推步,因此决不能认为最优权值也是一个时变量。它们类似于回归方程中的回归函数,一旦回归函数能够满足性能指标,它们应是时不变的。综上所述,算法2是正确的,而算法1和3都存在理解的偏差。
最后,还要指出,(3.8)中的 应满足:
应满足:

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















