面向复杂产品系统设计中的模块化及不确定性的决策方法

复杂产品系统设计与一般产品、简单大规模产品设计相比具有显著差异性,因此所面临的决策、评估、优化等问题具有高度的复杂性和不确定性。本节主要阐明复杂产品系统设计中出现的两类典型问题,并给出相应的基于软计算的决策方法。

第一类问题是模块化组合方案评估决策问题。在复杂产品系统设计过程中,为了实现零部件的有效重用,提高其核心技术和研发知识的重用率,降低产品改型演化设计的复杂度,通常采用模块化构造产品型谱的方式进行设计。但是由于复杂产品系统多组分、设计参数和设计约束繁多,模块化分解后会产生多组模块组合方案,因此寻求一种最优或满意的模块组合方案是产品设计成功的重要保证。通过将这类问题转换成多目标决策问题,充分利用各种软计算方法的推理和学习能力,并在决策目标可控范围内将各种软计算方法彼此结合,期待能在复杂产品的整体设计目标上最终解决模块化设计问题。

第二类问题是设计中的各类不确定性问题。复杂产品系统全生命周期过程属于多阶段、迭代式、高依赖的决策过程,决策过程中不但存在大量半结构化或非结构化问题,而且其原始数据信息存在多种不确定表达形式。如何从不确定信息的获取、表达、融合与推理出发,充分利用各种软计算方法和不确定性智能决策方法,将上述问题转化为不确定信息融合与推理、不确定多属性决策、案例推理、数据挖掘等智能决策问题,从而用已有的软计算决策理论方法予以解决,从而提高复杂产品系统全生命周期各阶段决策的置信度。

10.3.1复杂产品系统模块化方法

在复杂产品系统设计过程中,随着其核心技术的不断成熟和扩散,使用需求的不断提高,快速研制和生产同型谱所属不同变型的复杂产品系统是必然趋势,所以通常采用改型(变型)的策略进行设计。复杂产品系统多组分、多维度的复杂耦合特性,导致设计参数和设计约束繁多,设计方案多元化,因此有必要在对复杂产品系统特点进行深入分析的基础上,通过提高其核心技术和研发知识的重用率,实现零部件的有效重用,对缩短研发周期、提高研发质量具有重要促进作用。而现有的复杂产品系统设计型谱共性较低,造成复杂产品系统零部件标准化程度低,无法实现零部件的有效重用。

建立面向复杂产品系统的模块化设计方法体系,可以降低产品改型演化设计的复杂度,下文从该方法体系中涉及的三个关键技术(模块粗划分、模块详细划分及模块划分方案评价)出发,寻求一种以软计算方法集成为基础的协同决策解决方案。实现正确合理的不同粒度模块划分是复杂产品快速定制和产品族构造的基础,而有效的模块划分方案评价方法则是产品设计成败的重要保证,通过对模块划分方案的满意度进行不确定和不完全性的综合评判,选择最优(满意)的模块组合方式,使得评价过程和结果更加灵活、有效和合理。

复杂产品开发过程中常用的协调分解方法主要包括以下四种:

(1)协同优化(Collaborative Optimization,CO)包含一致性约束的、针对多学科耦合系统的两层协调求解策略。

(2)并行子空间优化(Concurrent Subspace Optimization,CSSO)则是采用全局灵敏度方程和近似模型相结合的方法,把整个系统按照不同学科划分成若干子空间,在每个子空间(子系统)的优化过程中,凡涉及该子空间的状态变量的计算,就用该学科的分析方法进行分析,而对于其他状态变量和约束则采用基于全局灵敏度方程的近似计算。

(3)二级集成系统综合法(Bi-Level Integrated System Synthesis,BLISS)把整个复杂产品的设计优化问题分解为系统级优化和子系统级优化,子系统级和系统级优化通过最优灵敏度导数相互联系,并且系统每次进行分析优化时都要进行一次多学科可行性分析,以保证系统优化的可行性。

(4)分级目标传递法(Analytical Target Cascading,ATC)根据设计系统的不同,由专业人员来确定整体设计优化级数的协调分解方法。不同的优化级数和子系统形成对设计空间的有效划分。

上述复杂产品系统的协调分解方法均有各自的优缺点,如何综合上述各类分解方法,建立一套相对完整、面向复杂产品系统设计习惯的模块分解的标准流程和技术体系,是有效解决所有产品设计问题的基础。面向复杂产品系统全生命周期的概念设计阶段实现模块化产品结构及功能构建前期规划,包括块划分(又称模块聚类、模块识别等)、模块优化与评价、模块型谱构建等问题,图10.6所示的是一种包含模块粗划分、模块详细划分及模块评价决策三个主体的方法体系。下面就从这三个方面简要说明各部分的主要内容。

图10.6　复杂产品系统模块化设计技术体系

模块粗划分的初衷主要是因为复杂产品系统,由于其元器件间的复杂关系,很难直接得到合理的模块划分结果或者快速得到划分结果,因此,应首先充分利用软计算处理不确定性的优势,例如使用基于模糊关系的聚类、基于目标函数的模糊聚类、基于神经网络的分析方法,实现复杂产品系统的初始模块划分。

模块详细划分在模块初次划分的基础上,主要针对复杂产品详细设计参数众多、涉及的数据量通常较大等特点,充分利用软计算方法能够综合运用推理和搜索方法处理海量数据的优势,选取与具体模块划分特征吻合的软计算方法,例如采用改进粒子群优化算法与模糊聚类法相结合的办法增强全局寻优能力,加快收敛速度,避免陷入局部最优。

模块划分方案决策优化主要针对复杂产品系统模块划分所产生的多个备选方案集的选择问题。由于模块划分过程中仅考虑了零部件间的功能和结构相关性,为了在复杂产品系统全生命周期中对模块划分方案的满意度进行不确定和不完全性的综合评判,需建立除功能和结构之外的模块划分方案评价指标体系,并结合多目标或多属性决策的优势,使评价的过程和结果更加灵活、有效和合理,得到的最优或满意模块划分方案符合复杂产品系统的设计要求。表10.1给出了一种用于复杂产品系统模块划分方案的评价指标体系。

表10.1　复杂产品系统模块划分方案评价指标体系

10.3.2　不确定多属性决策理论与方法

下文首先介绍多属性决策相关概念,然后针对复杂产品系统设计中的不确定性,说明常用的不确定多属性决策理论与方法,并对已建立的不确定多属性决策算法工具箱的功能进行阐述,最后面向复杂产品系统给出一种不确定决策的解题模式。

一般来说,多属性决策问题根据属性来评价方案,属性代表方案的特点和性质。为了评价方案,对每个属性设立一个准则,因为属性和准则相互对应,所以在多属性决策背景下,可以把属性和准则混同使用。多属性决策问题通常可以分为三种类型,即选择问题、排序问题和分类问题。它们的各自特点可以用图10.7表示。给定方案集A,选择问题是从A中找出最优(或满意)方案集;分类问题是将A中的每个方案根据其内在价值分派到预先定义的类型;排序问题是在A上建立一个偏序关系或者全序关系。虽然多属性决策问题的背景不同,但它们通常具有下列共同特点:

(1)属性之间通常是相互冲突和不可公度的(各属性的量纲不同);

(2)属性集中可能同时存在定性属性和定量属性;

(3)属性经常构成一个层次结构;

(4)决策信息有时是不完全的,决策者只能提供决策参数的不完全信息;

(5)决策者的判断可能是不确定的。

图10.7　多属性决策问题类型

上述这些特点决定了多属性决策问题通常比较复杂。根据决策者提供信息的充分程度,可将多属性决策方法分成无偏好信息的决策方法、有属性偏好信息的决策方法和给定方案之间偏好信息的决策方法三类。其中无偏好信息的决策方法包括Laplace准则、乐观准则、悲观准则和Hurwicz准则等,其中Hurwicz是介于乐观准则和悲观准则之间的一种判断方案优劣的准则;有属性偏好信息的决策方法包括标准水平规则、已知属性权重的序数信息和已知属性权重的基数信息三种形式;给定方案之间偏好信息的决策方法包括INMAP法、交互式简单加权法和带理想点的多维尺度法等,这类方法可通过决策者给出的方案成对地比较信息,求解线性规划问题,确定权重向量和最优方案。

经过多年研究和发展,基于序数和基数偏好的确定性决策问题已经形成了成熟的理论和方法,积累了丰富的研究成果。然而,随着决策问题的复杂性不断增加,决策者由于时间压力、认知水平及环境的不确定性等原因,往往难以准确表达自己的偏好信息,所以,不确定信息的决策问题成为研究热点。

在决策领域,Zimmermann给出了比较规范的关于不确定性的定义[33],即不确定性指在一个特定情形下,一个人没有拥有足够的定量或定性信息对一个系统及其行为或特征给出确定性的描述、规定和预测。复杂产品系统中的不确定性通常指不精确性、模糊性、信息不完全性(灰色)、随机性几类,具体到复杂产品系统设计的模块划分多属性决策过程中,可以有属性值为区间数和语言,权重完全未知和部分未知等形式。下面给出复杂产品系统的模块化设计中的不确定多属性决策的定义,记M＝{1,2,…m},N＝{1,2,…n},A＝(X,W,F)定义为一个具体的多属性决策问题,其中X＝{x 1,x 2,…x m}表示该多属性决策问题的方案集;W为属性权重集,W＝{ω1,ω2,…ωn},＝1;F为关系集F＝{f j|ωj→},其中为方案x i的第j个属性值,A为决策目标,当W和(或)F为不确定值时,该多属性决策问题转换成不确定多属性决策。不确定多属性决策的目标是从已知模块划分方案集X中得到一个满意方案、一组方案满意度的排序或方案的分类。

在复杂产品系统的模块化设计中涉及的多属性决策问题的方案集X一般已知确定,决策者需要根据权重W和关系F的信息得到决策结果。但由于种种原因,决策者往往不能给出精确决策信息,因此复杂产品系统的模块化设计中的不确定多属性决策有以下类别:

(1)属性权重完全未知　这种多属性决策没有给出关于属性的信息。

(2)仅有方案偏好的权重信息　这种决策没有直接给出属性权重,但决策者对方案有偏好,即对属性的偏好隐藏于对方案的偏好。

(3)属性权重信息不完全已知　属性权重的不完全信息包括以下情形:①ωi≥ωj;②ωi－ωj≥αi;③αi≤ωi≤αi＋εi。其中ωi,ωj分别对应于方案集中第i,j个属性值的权重,①和②中的ωi,ωj具有一定的可比相关性,③中描述的属性权重为区间形式,属性αi和εi为非负常数。

(4)可知属性之间的两两判断关系　这种情况没有直接给出属性权重,而是利用一定的标度对属性进行两两比较,得到判断矩阵,一般用于构造互反判断矩阵和模糊互补判断矩阵、残缺互补判断矩阵、混合判断矩阵等。

(5)属性权重表示为模糊数　常用的模糊数为梯形模糊数和三角模糊数。在决策者无法以精确值给出属性权重时,以模糊数表示权重是较好选择。

(7)属性为语言值决策者通过设定一组语言评估标度对决策问题进行测度。常用的语言标度有低、中、高,很差、差、一般、良好、优等。

(8)属性值为模糊数决策者评估方案的属性值时,不是给出确定数值,而是以梯形模糊数或三角模糊数的形式给出。

在完成复杂产品系统的模块划分后可得到模块组合方案集合,接下来需要通过一定的选择机制,从不确定决策方法库中选用适合当前具体方案评估任务的方法集合,由此切入备选方案集生成、评估和排序、进而运用单人(多人)决策方法等决策全生命周期过程。在建立的复杂产品系统协同决策支撑环境的支持下,不确定决策方法库的实际应用可以大大加快从定性的决策认知过程到定量的综合集成过程,迅速实现信息向知识的转变,而且基于个人理性决策的群体研讨决策使这个转变由盲目走向自觉、由直觉和经验走向理性和科学。后续介绍的不确定多属性工具包及决策实施过程中的方法分类粗筛选均以上述分类方法为指导,该分类未涉及的不确定多属性决策类型暂时不做研究。

10.3.3　复杂产品系统设计中的不确定决策解题模式

从复杂产品系统设计中的不确定决策所面临的问题入手,通过不确定多属性决策方法的运用,实现将不确定、动态、定性、粗略描述的高度复杂设计问题求解转化为确定、静态、定量、准确的全寿命周期决策和代数方程组问题求解,进而基于形式化和数值化构建决策者能准确描述的易于掌控的辅助工具集。结合具体复杂产品系统设计开发的先进管理方式,量身定制专用的决策支撑管理平台,为具体复杂产品系统的设计、分析、评价和决策提供科学有效的技术依据。

运用不确定多属性决策方法在复杂产品系统设计中的具体解题路线是:在设计决策问题空间中,将解决现实问题求解的描述归结为不确定多属性决策问题,决策者应确定属性集、权重、可能的算法,并收集相应信息,根据信息类别确定解的获取方式。

在复杂产品系统设计决策解空间中,按有限备选方案建立解空间,通过解的优化、研讨精化和集中群体智慧的方式,寻找决策者个体或群体的满意解。不确定多属性决策算法工具包可以支持决策者提升关于“问题—解”的知识深度,把不确定信息划分成不同类别的属性值、权重和算法分别加以处理,是将理论上的复杂产品系统决策问题工程化处理的一种务实方法,是一种通过可执行的简单数值计算、迭代逼近复杂问题的求解方法,也是一种定性与定量相结合的方法。

MATLAB在科学计算领域具有强大的功能,尤其在人工智能领域拥有众多功能强大的函数库,可以较为容易地实现功能非常复杂的不确定多属性决策算法,因此不确定多属性决策算法工具包采用MATLAB来实现相应的算法设计和运算。由于应用MATLAB实现的算法只能在MATLAB环境中运行,为了摆脱MATLAB对算法运行平台的限制,并且能够在B/S系统中使用,采用了组件编程的思想,应用MATLAB Builder for.NET将上述算法封装为COM组件,然后在Visual Studio开发工具中将不确定多属性决策算法COM组件包装成Web服务方式供分布式用户调用,实现B/S模式下的基于Web服务的不确定多属性决策算法工具包。不确定多属性决策算法的设计演化过程如图10.8所示。

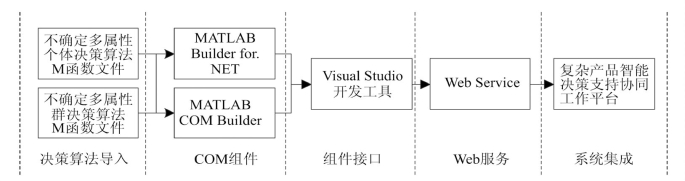
图10.8　不确定多属性决策算法设计演化过程

基于上述设计方案,在MATLAB软件的框架下,用MATLAB的M代码编写并编译实现各种不确定多属性决策算法模型,程序以M文件的形式存储,作为不确定多属性决策算法模型的源程序。编译后,利用MATLAB的.NET COM生成器将这些程序打包成COM组件,生成一个以组件名＋版本号＋DLL后缀为名称的动态链接库文件。此文件作为不确定多属性决策算法模型的目标程序,在.NET环境下通过标准接口,并按照Web服务的方式对其进行标准化处理,包装成Web服务方式供复杂产品智能决策支持协同工作平台中的各组分系统调用。

不确定多属性决策可以解决复杂产品系统设计中的一些不确定问题,但是并非万能。因此,对于某些无法建立有效指标描述体系或具有模糊性的问题,可以尝试与各种软计算技术协同和融合,共同完成复杂产品系统设计中的不确定问题。软计算是若干类以各种形式出现的计算方法,可以容忍部分不精确性以求得对系统具有合理性与可解释性的计算结果,不但各种软计算方法(例如FL、ANN、GA)可以有机互补,而且还能和其他方法(如不确定多属性决策、专家规则推理等)很好结合。例如专家决策的成功关键在于指标或规则的表示,但是指标或规则的提取和隶属函数的选择并不容易。可以通过神经网络的自学习和自组织性来解决这一问题,分类已知的训练数据并规定模糊规则的数量,用神经网络模糊分割输入空间,通过学习获取相应于所有规则的隶属函数的特性,并生成对应于任意输入矢量的隶属值,然后由神经网络的拟合功能产生相应的隶属函数。在此过程中,为了克服基于局部区域的梯度学习算法缺乏全局性和易陷入局部极小的缺陷,并且对网络结构进行优化,可以利用遗传算法来完善相应功能,获取最佳效果。反过来也可凭借模糊系统或神经网络的学习能力来设置遗传算法的各种参数,包括种群尺度、交叉概率、变异概率以及遗传算法的迭代次数等等。总之,将软计算方法和多属性决策方法有机结合能有效处理复杂产品系统中的非线性、不确定性问题。

10.3.3.1　决策算法导入

先根据预选的不确定多属性决策方法理论,设计其详细的算法流程,再依照MATLAB的语法编写算法MATLAB函数,编译无误后保存为M文件,例如基于离差最大化的多属性决策方法的M文件节选如下所示。

基于离差最大化的多属性决策方法

function[Z,Zorder,Zstand]＝chap1_5_1(A,I,IC)

10.3.3.2　封装决策算法组件

MATLAB Builder for.NET是MATLAB Compiler的扩展功能,能够从MATLAB算法代码自动生成独立的.NET assembly类库或Common Object Model(COM)对象。MATLAB Builder for.NET的主要功能包括:

(1)将用户的MATLAB算法应用程序转变为.NET或COM组件的图形界面工具;

(2)创建的.NET assembly类库可被C＃,VB.NET或其他Common Language Specification(CLS)兼容的语言调用;

(3)创建的COM对象可以被Visual Basic,ASPX,Microsoft Excel和其他COM兼容的环境调用;

(4)可将用MATLAB开发的算法封装的程序组件集成到桌面或Web应用环境;

(5)通过标准调用接口,在用户群间共享开发算法;

(6)可在应用程序中使用MATLAB开发的算法,无须运行或安装MATLAB软件。

MATLAB Builder for.NET同MATLAB,MATLAB toolboxes,MATLAB Compiler一起,为算法和应用程序的开发构建了一个集成化环境。MATLAB中面向矩阵运算优化的高级语言、内建算法、图形和数据分析函数等能有力支持算法的快速原型、开发和测试。MATLAB开发工具包括专门的代码编辑器,调试器和性能剖析器,任何时候用户都可以轻松修改MATLAB算法并重新生成基于MATLAB的组件。在目标机上安装MATLAB Component Runtime(MCR)后,无需安装MATLAB软件,用户就可以随意调用MATLAB Builder for.NET创建的MATLAB.NET或COM组件。Web应用程序服务器也同样适用。

将编写完毕的不确定多属性决策算法M文件转变为.NET assembly类库或COM对象的工作在MATLAB Builder for.NET图形用户界面(GUI)工具中完成。封装后的组件供其他计算机使用。每个组件都包括一个或多个类库。Builder for.NET GUI具有以下功能:

(1)添加M和MEX文件到组件类库;

(2)保存程序编译设置,再次使用时无需重新输入;

(3)在文件转换过程中显示所处状态并监视处理过程;

(4)组件构成文件的自动搜索和封装。

进行组件封装时用户可以选择手工添加相关文件,例如数据文件或文档。封装文件中可以包含MCR——用来支持Builder for.NET生成的文件在未安装MATLAB的平台上运行所用的计算引擎。

为了在没有安装MATLAB的计算机上使用编写的函数,需要生成以组件运行的MATLAB组件。点击部署工具窗体的设置按钮,弹出工程设置对话框,可以根据需要修改其中的某些参数。在这里,只需对Packaging参数进行设置,选择Include MATLAB Component Runtime就可以了,这样,在实际的打包过程中会自动包含MATLAB组件。返回部署工具窗体后点击Package图标,开始对.NET组件打包,过程结束后会生成自解压的打包程序。

10.3.3.3　调用生成的组件

当用MATLAB代码所创建的组件构造一个不确定多属性决策算法类库案例后,可以像调用访问其他COM或.NET类库一样使用其中所提供的类的方法。MATLAB Builder for.NET内含数据转换类库,使数据可以在原生的COM或.NET数据类型与MATLAB数组数据类型之间转换,或形成MATLAB数组数据输出。

在实现C＃.NET调用生成的MATLAB组件时,为了使MATLAB的COM组件在C＃.NET中能够被正常调用,首先要在解决方案资源管理器中添加“Math Works.NET MWArry API”和“Matlab Application Type Library”这两个引用。在Visual Studio开发平台建好的不确定多属性决策算法工具包项目工程下,找到解决方案视图,选择引用,点击右键,添加引用。在添加引用中的COM组件中找到已经生成的COM组件。将组件添加到工程中后,编写调用组件中函数的C＃代码。C＃代码主要负责调用其标准接口,系统的内部处理过程如图10.9所示,具体步骤如下:

(1)用户发送请求,根据“不确定多属性决策方法名称”确定该调用哪个组件;

(2)后台启动MATLAB进程;

(3)将输入参数转换成对应组件所要求的类型,并进行异常控制;

(4)将转换后的数据与MATLAB命令发送到MATLAB进行处理;

(5)将MATLAB的运算结果以用户要求的类型返回到C＃程序客户端;

(6)C＃程序客户端进行数据转换;

(7)C＃程序客户端将结果返回给用户。

这样做的好处是不确定多属性决策组件本身不用提供多种接口,用户也省了转换数据类型的麻烦,特别当不确定多属性决策方法更新后接口有变化时也不用对所有使用该方法的模块进行修改,降低了系统维护成本,提高了系统灵活性。

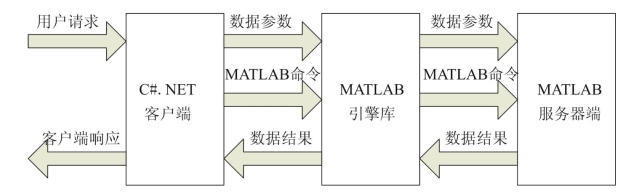
图10.9　C＃.NET调用MATLAB的内部处理过程

10.3.4　不确定多属性决策算法工具箱

通过把复杂产品系统设计决策中的不确定信息按属性值和权重划分成不同类别分别处理,建立的不确定多属性决策算法工具包可以支持决策者提升关于“问题—解”的知识深度,不但是将理论上的复杂产品系统设计决策问题工程化处理的一种务实方法,也是通过可执行的简单数值计算的迭代逼近复杂问题求解的一种定性与定量相结合的有效方法。

该工具包收入了基于OWA算子的多属性决策方法、基于信息熵的多属性决策方法、基于投影的区间值多属性决策方法、逼近理想点的区间值多属性决策方法、基于GIOWA算子的语言值多属性决策方法等业内普遍认可的多种常用多属性决策算法,并根据Web服务提供方式对其进行标准化,为了提高算法计算精度和效率,采用MATLAB作为Web服务计算平台,并对输入输出数据进行规范化处理。该工具包具有如下功能:

(1)根据问题建立树状指标体系(属性值表);

(2)属性值数据类型可以是精确定量、区间定量、模糊语言、不确定模糊语言四类,基本满足定性定量属性数据处理的要求;

(3)自动完成属性数据预处理,方法有线性变换、标准1－0变换、最优值在给定区间时的变换、向量规范化、原始数据的统计处理及专家打分数据的预处理等19种标准化预处理方法;

(4)自动处理属性权重和决策者权重,方法有OWA权重法、信息熵权重法、离差权重法等共34种计算方法,适用于不同情形下的多属性决策需求;

(5)使用工具包时,有在线主动提示和帮助。例如,关于当前问题所适用的算法的建议等。

表10.2和表10.3分别是该工具包中按决策属性集F和权重集W的不确定类型进行分类的部分决策算法说明。

表10.2　按决策属性集F分类的工具包算法说明

表10.3　按权重集F分类的工具包算法说明

在设计的不确定多属性决策算法工具箱中,除了上述提到的不确定多属性决策算法外,还包括对决策属性值进行标准化处理的算法模块。因为多属性决策有两个显著特点,即属性间的不可公度性和属性间的矛盾性。所谓不可公度性是指各个属性没有统一的度量标准,不能直接比较。矛盾性是指如果采用一种方法去改进某一属性上的值,可能会使另一属性上的值变坏。由于不同量纲的影响,决策矩阵的规范化处理是多属性决策中不可缺少的一个重要环节。

决策属性的种类通常有效益型、成本型、固定型、区间型、偏离型、偏离区间型。所谓效益型属性是指越大越好的属性,成本型属性是指越小越好的属性,固定型属性是指越接近某值越好的属性,偏离型属性是指越偏离某值越好的属性,区间型属性是指越接近某区间越好的属性,偏离区间型属性是指越远离某区间越好的属性。

不确定多属性决策算法工具箱对实数型属性标准化方法实现Web服务化,形成实数型属性标准化方法Web服务库,通过采用这种基于Web服务方法组件化的形式,今后可以灵活地进行属性标准化的更新和增加,具体的实数型属性标准化计算公式可参考表10.4。

表10.4　实数型属性标准化方法

续表