事件的相互独立性

一般来说，P（A｜B）≠P（A）（P（B）＞0）），这表明事件B的发生提供了一些信息影响了事件A发生的概率．但是有些情况下，P（A｜B）＝P（A），从这可以想象得到这必定是事件B的发生对事件A的发生不产生任何影响，或不提供任何信息，也即：事件A与事件B是‘无关’的．从概率上讲，这就是事件A与事件B相互独立．

定义1．3．3 若两事件A，B满足P（AB）＝P（A）P（B），则称事件A与B是相互独立的．

容易知道，若P（A）＞0，P（B）＞0，则如果A，B相互独立，就有P（AB）＝P（A）P （B）＞0，故AB≠∅，即A，B相容．反之，如果A，B互不相容，即AB＝∅，则P（AB）＝0，而P（A）P（B）＞0，所以P（AB）≠P（A）P（B），即A与B不独立．这就是说若P（A）＞0且P（B）＞0，则A，B相互独立与A，B互不相容不能同时成立．事件的独立性是从概率的意义下来定义的，是指一个事件的发生与否不影响另一事件发生的概率，不要把它与“两个事件不相容”混淆．事件的相容性是由事件的运算关系描述的．说两个事件不能同时发生，与概率无关．

定理1．3．4 若事件A、B相互独立，且P（B）＞0，则

定理1．3．5 若事件A、B相互独立，则下列各对事件也相互独立：A与与B，与

由对称性，A与B也相互独立．

即与相互独立．

定义1．3．4 对于3个事件A、B、C，若满足下面4个等式：

P（AB）＝P（A）P（B）；

P（AC）＝P（A）P（C）；

P（BC）＝P（B）P（C）；

P（ABC）＝P（A）P（B）P（C）．

则称A、B、C为相互独立的事件．

这里要注意，若事件A、B、C仅满足定义中前3个等式，则称A、B、C是两两独立的．由此可见，A、B、C为相互独立，则A、B、C是两两独立的．但反过来，则不成立．

定义1．3．5 设有n个事件A1，A2，…，An（n≥3），若对其中任意两个事件Ai与Aj （1≤i＜j≤n）有

P（AiAj）＝P（Ai）P（Aj）．

则称这n个事件是两两相互独立的．

定义1．3．6 对于任意n个事件，A1，A2，…，An，若下面2n－n－1个等式成立：

P（AiAj）＝P（Ai）P（Aj），1≤i＜j≤n；

P（AiAjAk）＝P（Ai）P（Aj）P（Ak），1≤i＜j＜k≤n；



P（A1A2…An）＝P（A1）P（A2）…P（An）．

则称A1，A2，…，An是相互独立的事件．

由上述定义可知，若n个事件A1，A2，…，An相互独立，则n个事件一定是两两相互独立；反之，却不一定成立．

由定义可知，

（1）若n个事件A1，A2，…，An（n≥2）相互独立，则其中任意k（2≤k≤n）个事件也相互独立；

（2）若n个事件A1，A2，…，An（n≥2）相互独立，则将A1，A2，…，An中任意多个事件换成它们的对立事件，所得的n个事件仍相互独立．

解 设A＝｛三人中至少有一人能译出密码｝，则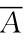＝｛三人中无人能译出密码｝，再设B1＝｛甲能译出密码｝，B2＝｛乙能译出密码｝，B3＝｛丙能译出密码｝．

A＝由题可判断B1，B2，B3相互独立，故