区间估计的基本概念

参数的点估计值给出了一个具体的数值，便于计算和使用，但点估计值本身只是未知参数的一个近似值．人们在测量或计算时，常不以得到近似值为满足，还需估计误差，即要求知道近似值的精确程度．因此，对于未知参数θ，除了求出它的点估计θ＾外，我们还希望估计出一个范围，并希望知道这个范围包含参数θ真值的可信程度．

设θ＾为未知参数θ的估计量，其误差小于某个正数ε的概率为1－α（0＜α＜1），即

或

这表明，随机区间包含参数θ真值的概率（可信程度）为1－α，则这个区间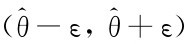就称为置信区间，1－α称为置信水平．

定义7．3．1 设总体X的分布中含有一个未知参数θ．若对于给定的概率1－α（0＜α＜1），存在两个统计量使得

则随机区间称为参数θ的置信水平为1－α的置信区间，称为置信下限，称为置信上限，1－α称为置信水平或置信度．

注7．3．1 （1）置信区间的含义若反复抽样多次（各次的样本容量相等，均为n），每一组样本值确定一个区间每个这样的区间要么包含θ的真值，要么不包含θ的真值．按伯努利大数定理，在这么多的区间中，包含θ真值的约占100（1－α）％，不包含θ真值的约仅占100α％．例如：若α＝0．01，反复抽样1000次，则得到的1000个区间中，不包含θ真值的约为10个．

（2）置信区间的长度表示估计结果的精确性，而置信水平表示估计结果的可靠性．对于置信水平为1－α的置信区间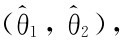一方面置信水平1－α越大，估计的可靠性越高；另一方面区间的长度（2ε）越小，估计的精确性越好．我们自然希望反映可信程度越大越好，反映精确程度的区间长度越小越好．但在实际问题，二者常常不能兼顾，提高可靠性通常会使精确性下降（区间长度变大），而提高精确性通常会使可靠性下降（1－α变小），所以要找两方面的平衡点．

在学习区间估计方法之前，我们先介绍标准正态分布的上α分位点概念．

设X～N（0，1），若zα满足条件P｛X＞zα｝＝α，0＜α＜1，则称点zα为标准正态分布的上α分位点．例如求z0．01．按照α分位点定义，我们有P｛X＞z0．01｝＝0．01，则P｛X≤z0．01｝＝0．99，即∅（z0．01）＝0．99．查表可得z0．01＝2．327．

例7．3．1 设X1，X2，…，Xn来自总体X～N（μ，σ2）的一个样本，其中σ2已知，μ为未知参数，求μ的置信度为1－α的置信区间（这里α＝0．05）．

解 由第六章我们知道，X是μ的无偏估计，且有

据标准正态分布的α分位点的定义有：

即

由α＝0．05，查表得：zα2＝z0．025＝1．96．

又若σ＝1，n＝16，x＝5．4则得到一个置信度为0．95的置信区间为：