假设检验与区间估计

回顾第七章介绍的有关参数的区间估计和本章前面介绍的假设检验内容，我们可以发现，这两者之间有着非常密切的联系，首先，我们来看方差已知时单个正态总体均值的统计推断问题。

而有关均值μ的双边假设检验问题

的显著水平为α的检验的拒绝域为

从而检验的接受域为

如果把接受域中的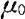改写成μ所得结果正好是μ的置信水平为1－α的置信区间。反过来，我们也可由μ的置信水平为1－α的置信区间的结果推得μ的假设检验问题显著水平为α的检验的接受域。

一般来说，设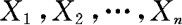为来自总体X～F（x；θ）的样本。若双边假设问题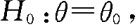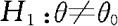的水平为α的检验的接受域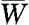能等价地写成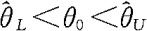的形式，那么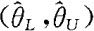是θ的置信水平为1－α的置信区间，反之，若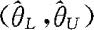是θ的置信水平为1－α的置信区间，则当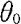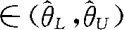时，我们没有充分的把握认为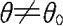，因此我们接受原假设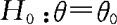。显然，这个检验的拒绝域为

若左边假设问题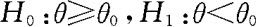的水平为α的检验的接受域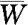能等价地写成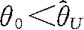的形式，那么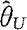是θ的置信水平为1-α的单侧置信上限。反之，若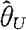是θ的置信水平为1-α的单侧置信上限，当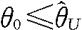时，接受原假设。

若右边假设问题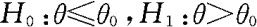的水平为α的检验的接受域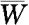能等价地写成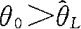的形式，那么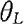是θ的置信水平为1-α的单侧置信下限。反之，若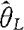是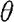的置信水平为1-α的单侧置信下限，则当时，接受原假设。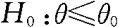

例8.4.1　某种元件的寿命X（以小时记）服从正态分布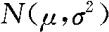，μ和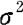均未知。现测得16只元件的寿命如下：

试给出μ的置信水平为95％的下侧置信限，并推断是否有充分的理由认为元件的平均寿命大于225小时？

解　根据第七章的知识可得μ的置信水平为95％的下侧置信限

查t分布表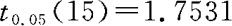，并将样本资料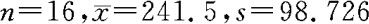代入得μ的置信水平为95％的下侧置信限为198.230。由于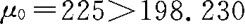，因此，没有充分的理由认为元件的平均寿命大于225小时。

例8.4.2　为了研究某种止痛药的副作用，调查了服用止痛药的440名患者，发现有23名出现了“反症状”。那么，是否有足够的理由说明在服用止痛药的病人中，出现“反症状”的比例低于10％？（α＝0.05）

解　这是有关二点分布B（1，p）中参数p的假设检验问题。由题意知，可以考虑左边假设

根据§7.5节中有关二点分布B（1，p）中参数p的区间估计的结果可得，p的置信水平为1-α的单侧置信上限为

其中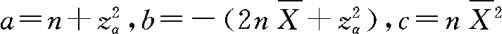。将已知资料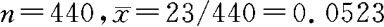，并取α＝0.05，代入上式计算得。

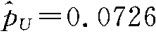根据假设检验与区间估计的关系知，此时有关p的左边假设检验问题的检验规则为：当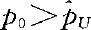时拒绝原假设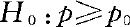。由于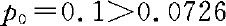，因此，我们作出拒绝原假设的判断，即认为在服用止痛药的病人中，出现“反症状”的比例明显低于10％。