基于算法的流场数值计算

第7章　数学模型的求解与数据的后处理方法

通过前几章的介绍，我们已经对气固两相流动的数学模型有了初步的认识，但如何求解这些复杂的数学模型，又如何用计算机处理数值模拟所获得的计算结果，这些问题将在本章进行讨论。

7.1　基于欧拉框架下的连续相求解

气相场的数学模型主要包括：连续性方程、动量守恒方程等。如果流动处于湍流状态，模型中还应附加湍流输运方程。气相场求解的核心任务便是获得这些模型所构成的偏微分方程组的解，但由于所处理问题自身的复杂性，如复杂的边界条件或者方程自身的复杂性，往往造成很难获得方程组的真解。随着数值方法和计算机技术的快速发展，采用计算流体力学（Computational　Fluid　Dynamics，简称CFD）的相关知识能够有效求解这些偏微分方程组，并可以作为分析流体流动和热传导等相关物料现象的手段之一。该学科的基本思想可以归结为：把原来在时间域及空间域上连续的物理量的场，如速度场和压力场，用一系列有限个离散点上的变量值的集合来代替，通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数方程组，然后求解代数方程组获得场变量的近似值。

7.1.1　计算流体力学的求解过程

为了进行CFD计算，读者可借助商用软件来完成所需要的任务，也可自己直接编写计算程序。两种方法的基本工作过程是相同的。本节给出基本计算思路，至于每一步的详细过程，可以参考相关书籍。

1）总体计算流程

气相流动系统，无论是稳态问题还是瞬态问题，其求解过程都可用图7－1表示。

如果所求解的问题是瞬态问题，则可将图7－1的过程理解为一个时间步的计算过程，循环这一过程可求解下个时间步。下面对各求解步骤做一简单介绍。

2）CFD工作流程分析

（1）建立控制方程

图7－1　CFD工作流程图

建立控制方程是求解任何问题前都必须首先进行的。一般来讲，这一步是比较简单的。因为对于一般的流体流动而言，可根据5.2节直接写出其控制方程。若假定没有热交换发生，则可直接将连续性方程与动量方程作为控制方程使用。当然，由于工业设备的流动大多是处于湍流范围，因此，一般情况下需要增加湍流方程。

（2）确定初始条件与边界条件

初始条件与边界条件是控制方程有确定解的前提，控制方程与相应的初始条件、边界条件的组合构成对一个物理过程完整的数学描述。

初始条件是所研究对象在过程开始时刻各个求解变量的空间分布情况。对于瞬态问题，必须给定初始条件；对于稳态问题，不需要初始条件。

边界条件是在求解域的边界上所求解的变量或其导数随地点和时间的变化规律。对于任何问题，都需要给定边界条件。例如，对于在锥管内的流动，在锥管进口断面上我们可给定速度、压力沿半径方向的分布，而在管壁上可对速度取无滑移边界条件。

（3）划分计算网格，生成计算节点

采用数值方法求解控制方程时，都是想办法将控制方程在空间域上进行离散化，然后求解得到的离散方程组。要想在空间域上离散化控制方程，必须使用网格。现已发展出多种对各种区域进行离散化以生成网格的方法，统称为网格生成技术。

不同的问题采用不同数值解法时，所需要的网格形式是有一定区别的，但生成网格的方法基本是一致的。目前，网格分结构网格和非结构网格两大类。简单地讲，结构网格在空间上比较规范，如对一个四边形区域，网格往往是成行成列分布的，行线和列线比较明显。而对于非结构网格，在空间分布上没有明显的行线和列线。

对于二维问题，常用的网格单元有三角形和四边形等形式；对于三维问题，常用的网格单元有四面体、六面体、三棱体等形式。在整个计算域上，网格通过节点联系在一起。

目前各种CFD软件都配有专用的网格生成工具，如FLUENT使用GAMBIT作为前处理软件。多数CFD软件可接收采用其他CAD或CFD/FEM软件产生的网格模型，如FLUENT可以接收ANSYS所生成的网格。

（4）建立离散方程

对于在求解域内所建立的偏微分方程，理论上其是有真解（或称精确解或解析解）的。但由于所处理的问题自身的复杂性，一般很难获得方程的真解。因此，就需要通过数值方法把计算域内有限数量位置（网格节点或网格中心点）上的因变量值当作基本未知量来处理，从而建立一组关于这些未知量的代数方程组，然后通过求解代数方程组来得到这些节点值，而计算域内其他位置上的值则根据节点位置上的值来确定。

由于所引入的因变量在节点之间的分布假设及推导离散化方程的方法不同，就形成了有限差分法、有限元法、有限体积法等不同类型的离散化方法。

在同一种离散化方法中，如在有限体积法中，对控制方程所采用的离散格式不同，也将导致最终有不同形式的离散方程。

（5）离散化初始条件和边界条件

前面所给定的初始条件和边界条件是连续性的，如在静止壁面上速度为0，现在需要针对所生成的网格，将连续型的初始条件和边界条件转化为特定节点上的值，如静止壁面上共有90个节点，则这些节点上的速度值应均设为0。这样，连同所建立的离散化的控制方程，才能对方程组进行求解。

在商用CFD软件中，往往在前处理阶段完成了网格划分后，直接在边界上指定初始条件和边界条件，然后由前处理软件自动将这些初始条件和边界条件按离散的方式分配到相应的节点上去。

在7.1.4节将结合FLUENT软件对如何处理初始条件和边界条件进行分析并给出应用实例。

（6）给定求解控制参数

在离散空间上建立了离散化的代数方程组并施加离散化的初始条件和边界条件后，需要给定流体的物理参数和湍流模型的经验系数等。此外，还要给定迭代计算的控制精度、瞬态问题的时间步长和输出频率等。

（7）求解离散方程

在进行了上述设置后，生成了具有定解条件的代数方程组。对于这些方程组，数学上已有相应的解法，如线性方程组可采用高斯（Gauss）消去法或高斯－赛德尔（Gauss－Seidel）迭代法求解，而对于非线性方程组，可采用牛顿－拉夫逊（Newton－Raphson）方法。在商用CFD软件中，往往提供多种不同的解法以适应不同类型的问题。这部分内容属于求解器设置的范畴。

（8）判断解是否收敛

对于稳态问题的解或是瞬态问题在某个特定时间步上的解，往往要通过多次迭代才能得到。有时，因网格形式或网格大小、对流项的离散插值格式等原因，可能导致解的发散。对于瞬态问题，若采用显式格式进行时间域上的积分，当时间步长过大时，也可能造成解的振荡或发散。因此，在迭代过程中要对解的收敛性随时进行监视，并在系统达到指定精度后结束迭代过程。

这部分内容属于经验性的，需要针对不同情况进行分析。

（9）显示和输出计算结果

通过上述求解过程得出了各计算节点上的解后，需要通过适当的手段将整个计算域上的结果表示出来。这时，我们可采用线值图、矢量图、等值线图、流线图、云图等方式对计算结果进行表示。

所谓线值图，是指在二维或三维空间上，将横坐标取为空间长度或时间历程，将纵坐标取为某一物理量，然后用光滑曲线或曲面在坐标系内绘制出某一物理量沿空间或时间的变化情况。矢量图是直接给出二维或三维空间里矢量（如速度）的方向及大小，一般用不同颜色和长度的箭头表示速度矢量，它可以比较容易地让用户发现其中存在的旋涡区。等值线图是用不同颜色的线条表示相等物理量（如温度）的一条线。流线图是用不同颜色线条表示质点运动轨迹。云图是使用渲染的方式，将流场某个截面上的物理量（如压力或温度）用连续变化的颜色块表示其分布。

现在的商用CFD软件均提供了上述各表示方式。用户也可以自己编写后处理程序进行计算结果显示。

7.1.2　基于有限体积法的计算区域及控制方程的离散

在CFD求解中用得较多的数值方法有：有限差分法（Finite Difference Method，FDM）、有限体积法（Finite Volume Method，FVM）、有限元法（Finite Element Method，FEM）及有限分析法（Finite Analytic Method，FAM）。

其中，有限体积法在商业CFD软件领域的应用最为广泛，如PHOENICS、FLUENT、STAR－CD和CFX都是常用的有限体积法软件。

在有限体积法中，将所计算的区域划分成一系列控制体积，每个控制体积都有一个节点作代表，通过将守恒型的控制方程对控制体积作积分来导出离散方程。在导出过程中，需要对界面上的被求函数本身及其一阶导数的构成作出假定，这种构成的方式就是有限体积法中的离散格式。用有限体积法导出的离散方程可以保证具有守恒特性，而且离散方程系数的物理意义明确，是目前在流动与传热问题的数值计算中应用最广泛的一种方法。

从上面的简介看到，有限体积法是一种分块近似的计算方法，其中比较重要的步骤是计算区域离散化和控制方程离散化。

1）计算区域离散化

所谓区域离散化（domain discretizntion），实质上就是用一组有限个离散的点来代替原来的连续空间。一般的实施过程是：把所计算的区域分成许多个互不重叠的子区域（sub－domain），确定每个子区域中的节点位置及该节点所代表的控制体积。区域离散后，得到以下4种几何要素。

（1）节点（node）：需要求解的未知物理量的几何位置。

（2）控制体积（control volume）：应用控制方程或守恒定律的最小几何单位。

（3）界面（face）：它定义了与各节点相对应的控制体积的界面位置。

（4）网格线（grid line）：连接相邻两节点面形成的曲线簇。

一般把节点看成控制体积的代表，在离散过程中，将一个控制体积上的物理量定义并存储在该节点处。图7－2给出了一维问题的有限体积计算网格，图7－3给出了二维问题的有限体积法计算网格。

图7－2　一维的有限体积法计算网格

图7－3　二维的有限体积法计算网格

计算区域离散的网格有两类：结构化网格和非结构化网格。节点排列有序，即当给出了一个节点的编号后，立即可以得出其相邻节点的编号，所有内部节点周围的网格数目相同，这种网格称为结构化网格（structured grid）。结构化网格具有实现容易、生成速度快、网格质量好、数据结构简单的优点，但不能实现复杂边界区域的离散。

而非结构化网格的内部节点以一种不规则的方式布置在流场中，各节点周围的网格数目不尽相同。这种网格虽然生成过程比较复杂，但却有极大的适应性，对复杂边界的流场计算问题特别有效。

2）控制方程离散化

第5章给出的关于流体流动问题的控制方程，无论是连续性方程、动量方程还是能量方程，都可写成如式（7－1）所示的通用形式，

对于一维稳态问题，其控制方程如式（7－2）所示：

式中，从左到右各项分别为对流项、扩散项和源项。方程中的φ是广义变量，可以为速度、温度或浓度等一些待求的物理量；Γ是相应于φ的广义扩散系数，S是广义源项。变量φ在端点A和B的边界值为已知。

有限体积法的关键一步是在控制体积上积分控制方程，在控制体积节点上产生离散的方程。对于一维模型方程（7－2），在图7－2所示的控制体积P上作积分，有

式中，ΔV是控制体积的体积值。当控制体积很微小时，ΔV可以表示为ΔV·A，这里A是控制体积界面的面积。从而有

从式（7－4）看到，对流项和扩散项均已转为控制体积界面上的值。有限体积法最显著的特点之一就是离散方程中具有明确的物理插值，即界面的物理量要通过插值的方式由节点的物理量来表示。

为了建立所需要形式的离散方程，需要找出如何表示式（7－4）中界面e和w处的ρ，u，Γ，。在有限体积法中规定，ρ，u，Γ，φ和dφd x等物理量均是在节点处定义和计算的。因此，为了计算界面上的这些物理参数（包括其导数），需要一个物理参数在节点间的近似分布。可以想象，线性近似是可以用来计算界面物性值的最直接也是最简单的方式。这种分布叫作中心差分。如果网格是均匀的，则单个物理参数（以扩散系数Γ为例）的线性插值结果是

（ρuφA）的线性插值结果是

与梯度项相关的扩散通量的线性插值结果是

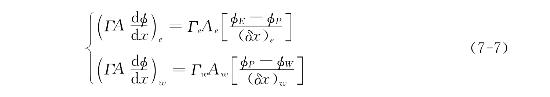
对于源项S，它通常是时间和物理量φ的函数。为了简化处理，将S转化为如下线性方程：

S＝SC＋SPφP　　　（7－8）

式中，SC是常数，SP是随时间和物理量φ变化的项。将式（7－5）～式（7－8）代入方程（7－4），有

整理后得

记为

aPφP＝aWφW＋aEφE＋b　　（7－10）

式中：

对于一维问题，控制体积界面e和w处的面积Ae和Aw均为1，即单位面积。这样，ΔV＝Δx，式（7－11）中各系数可转化为

方程（7－10）即为方程（7－2）的离散形式；每个节点上都可建立此离散方程，通过求解方程组，就可得到各物理量在各节点处的值。

为了后续讨论的方便，定义两个新的物理量F和D，其中F表示通过界面上单位面积的对流质量通量（convective mass flux），简称对流质量流量；D表示界面的扩散传导性（diffusion conductance）。定义表达式如下：

这样，F和D在控制界面上的值分别为

在此基础上，定义一维单元的贝克来（Peclet）数Pe如下：

式中，Pe表示对流与扩散的强度之比。当Pe数为0时，对流－扩散演变为纯扩散问题，即流场中没有流动，只有扩散；当Pe＞0时，流体沿x方向流动，当Pe数很大时，对流－扩散问题演变为纯对流问题。一般在中心差分格式中，有Pe＜2的要求。

将式（7－13）代入方程（7－12），有

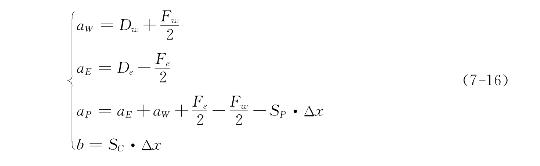
对于瞬态问题，与稳态问题相似，主要是瞬态项的离散。其一维瞬态问题的通用控制方

程如下：

该方程是一个包含瞬态及源项的对流－扩散方程。从左到右，方程中的各项分别是瞬态项、对流项、扩散项及源项。方程中的φ是广义变量，如速度分量、温度、浓度等；Γ为相应于φ的广义扩散系数；S为广义源项。

对瞬态问题用有限体积法求解时，在将控制方程对控制体积作空间积分的同时，还必须对时间间隔Δt作时间积分。对控制体积所作的空间积分与稳态问题相同，这里仅叙述对时间的积分。

将方程（7－17）在一维计算网格上对时间及控制体积进行积分，有

改写后，有

式中，A是图7－2中控制体积P的界面处的面积。

在处理瞬态项时，假定物理量φ在整个控制体积P上均具有节点处值φP，并用线性插值）/Δt来表示aφ/at。源项也分解为线性方程S＝Sc＋SPφP。对流项和扩散项的值按中心差分格式通过节点处的值来表示，则有

假定变量φP对时间的积分为

式中，上标0代表t时刻；φP是该时刻的值；f为0与1之间的加权因子，当f＝0时，变量取老值进行时间积分，当f＝1时，变量采用新值进行时间积分。

将φP，φE，φW及SC＋SPφP采用类似式（7－21）的方式进行时间积分，式（7－20）可写成

整理后得

同样，引入稳态问题中关于符号F和D的定义，并将原来的定义作一定扩展，即乘以面积A，有

将式（7－24）代入方程（7－23），得

同样，也像稳态问题中那样引入aP，aW和aE，式（7－25）变为

式中：

根据f的取值，瞬态问题对时间的积分有几种方案：当f＝0时，变量的初值出现在方程（7－26）的右端，从而可直接求出在现时刻的未知变量值，这种方案称为显式时间积分方案。当0＜f＜1时，现时刻的未知变量出现在方程（7－26）的两端，需要解若干个方程组成的方程组才能求出现时刻的变量值，这种方案称为隐式时间积分方案；当f＝1时，就成为了全隐式时间积分方案了；当f＝1/2时，称为Crank－Nicolson时间积分方案。

进一步将一维问题扩展为二维与三维问题。在二维问题中，计算区域离散如图7－4（a）所示。可以发现只是增加了第二坐标y，控制体积增加的上下界面分别用n（north）和s（south）表示，相应的两个邻点记为N和S。在全隐式时间积分方案下的二维瞬态对流－扩散问题的离散方程为

图7－4　计算区域的离散

式中：

在三维问题中，计算区域离散如图7－4（b）所示（两个方向的投影）。在二维的基础上增加第三坐标z，控制体积增加的前后界面分别用t（top）和b（bottom）表示，相应的两个邻点记为T和B。在全隐式时间积分方案下的三维瞬态对流－扩散问题的离散方程为

式中：

7.1.3　基于SIMPLE算法的流场数值计算

建立了与气相场控制方程相应的离散方程之后，除了如已知速度场求温度分布这类简单问题之外，所生成的离散方程不能直接用来求解，还必须对离散方程进行某种调整，并且对各未知量（速度、压力、温度等）的求解顺序及方式进行特殊处理。为此，本节将详细介绍工程上应用最广泛的流场计算方法——求解压力耦合方程组的半隐式方法（SIMPLE算法）。

1）交错网格

使用交错网格，主要是为了解决在普通网格上离散控制方程时不能检测有问题的压力场的问题。同时，交错网格也是SIMPLE算法实现的基础。

所谓交错网格（staggered grid），就是将标量（如压力p、温度T和密度等）在正常的网格节点上存储和计算，而将速度的各分量分别在错位后的网格上存储和计算，错位后网格的中心位于原控制体积的界面上。这样对于二维问题，就有三套不同的网格系统，分别用于存储p，u和v；而对于三维问题，就有四套网格系统，分别用于存储p，u，v，w。

二维流动计算的交错网格系统如图7－5所示，主控制体积为求解压力p的控制体积，称为标量控制体积（scale control volume）或p控制体积，控制体积的节点P称为主节点或标量节点（scale node）［如图7－5（a）所示］。速度u在主控制体积的东、西界面e和w上定义和存储，速度v在主控制体积的南、北界面s和n上定义和存储。u和v各自的控制体积则是分别以速度所在位置（界面e和界面n）为中心的，分别称为u控制体积（u－control volume）和v控制体积（v－control　volume），如图7－5（b）和（c）所示。可以看到，u控制体积和v控制体积是与主控制体积不一致的，u控制体积与主控制体积在x方向上有半个网格步长的错位，而v控制体积与主控制体积则在y方向上有半个步长的错位。

图7－5　控制体积

图7－6中所示的均匀网格是向后错位的，因为u控制体积的速度ui，J的i位置到标量节点（I，J）的距离是－1/2δxu；同样，v控制体积的速度vI，j的j位置到标量节点（I，J）的距离是－1/2δyv。当然，也可以选用向后两个错位的速度网格。

在使用了上述交错网格后，生成离散方程的方法和过程与原来的基于普通网格的方法和过程是一样的，只是需要注意所使用的控制体积有所变化。在交错网格中，由于所有标量（如压力、温度、密度等）仍然在主控制体积上存储，因此，以这些标量为因变量的输运方程的离散过程及离散结果与前面的一样。主要是在交错网格中生成u和v两个动量方程的离散方程时，积分用的控制体积不再是原来的主控制体积，而是u和v各自的控制体积，同时压力梯度项从源项中分离出来。例如，对u控制体积，该项积分为－pI，J）Ai，J。从而，对于方程（7－10）的离散方程，对u方向的动量方程使用u控制体积，可以写出在位置（i，J）处的关于速度ui，J的动量方程的离散形式如下：

图7－6　交错网格

式中，Ai，J是u控制体积的东界面或西界面的面积，在二维问题中实际上是Δy，即

式（7－32）中的b为u动量方程的源项部分（不包括压力在内）。对于稳态问题，有

bi，J＝SuCΔVu　　　（7－34）

式（7－34）中的SuC是对源项Su线性化分解的结果，若Su不随速度u而变化，则有SuC≥Su，SuP＝0。式（7－34）中的ΔVu是u控制体积的体积。式（7－32）中的压力梯度项已经按线性插值的方式进行了离散，线性插值时使用了u控制体积边界上的两个节点的压力差。

在求和记号中所包含的E，W，N和S四个邻点是（i－1，J），（i＋1，J），（i，J＋1）和（i，J－1），它们的位置及主速度在图7－7中标出。图中阴影部分是u控制体积。图7－7中的u控制体积与图7－6中是一致的，这可从节点的编号看出。但是，图7－7 中u控制体积的中心也用P来标记，其界面点也用e，w，n和s来标记，这里的标记与图7－6中的同名标记及系数a是由式（7－10）给定的。即

图7－7　u控制体积及其邻点的速度分量

系数anb取决于所采用的离散格式，在计算公式中含有u控制体积界面上的对流质量流量F与扩散导性D，在采用新编号系统下的计算公式为

采用交错网格对动量方程离散时，涉及不同类别的控制体积，不同的物理量分别在各自相应的控制体积的节点上定义和存储。例如，密度是在标量控制体积的节点上存储的，如图7－7中的标量节点（I，J）；而速度分量却是在错位后的速度控制体积的节点上存储的，如图7－7中的速度节点（i，J）。这样就会出现这种情况：在速度节点处不存在密度值，而在标量节点处找不到速度值，当在某个确定位置处的某个复合物理量［如式（7－36）中的流通量F］同时需要该处的密度及速度时，要么找不到该处的密度，要么找不到该处的速度。为此，需要在计算过程中通过插值来解决。式（7－36）表明，标量（密度）及速度分量在u控制体积的界面上是不存在的，这时，根据周边的最近邻点的信息，使用两点或四点平均的办法来处理。

在每次迭代过程中，用于估计上述各表达的速度分量u和速度分量v是上一次迭代后的数值（在首次迭代时是初始猜测值）。需要特殊说明的是，这些“已知的”速度值u和v也用于计算方程（7－32）中的系数a，但是它们与方程（7－32）中的待求uj，J和unb是完全不同的。

还需要说明的是，式（7－36）中的线性插值是基于均匀网格而言的，若网格是不均匀的，应该将式（7－36）中的系数2和4等改为相应的网格长度或宽度值的组合。例如，对于不均匀网格上的Fw，按式（7－37）计算：

按上述同样的方式，可以写出在新的编号系统中，在位置（I，j）处的关于速度vI，j的离散动量方程：

建立式（7－38）所使用的v控制体积表示在图7－8中。

在求和记号中所包含的4个邻点及其主速度也图7－8中标出。在系数aI，j和anb中，同样包含在v控制体积界面上的对流质量流量F与扩散传导性D，计算公式如下：

图7－8　v控制体积及其邻点的速度分量

同样，在每个迭代层次上，用于估计上述各表达式的速度分量u和速度分量v均取上一次迭代后的数值（在首次迭代时是初始猜测值）。

给定一个压力场p，便可针对每个u控制体积和v控制体积写出式（7－32）和式（7－38）所示的动量方程的离散方程，并可以从中求解出速度场。如果压力场是正确的，则所得到的速度场将满足连续性方程。

2）SIMPLE算法

SIMPLE算法是目前工程上应用最为广泛的一种流场计算方法，它属于压力修正法的一种。

SIMPLE是英文Semi－Implicit Method for Pressure－Linked Equations的缩写，意为“求解压力耦合方程组的半隐式方法”。该方法由Patankar与Spalding于1972年提出，是一种主要用于求解不可压流场的数值方法（也可用于求解可压流动）。它的核心是采用“猜测—修正”的过程，在交错网格的基础上来计算压力场，从而达到求解动量方程（纳维－斯托克斯方程）的目的。

SIMPLE算法的基本思想可描述如下：对于给定的压力场（它可以是假定的值，或是上一次迭代计算所得到的结果），求解离散形式的动量方程，得出速度场。因为压力场是假定的或不精确的，这样一来，由此得到的速度场一般不满足连续性方程，因此必须对给定的压力场加以修正。修正的原则是：与修正后的压力场相对应的速度场能满足这一迭代层次上的连续性方程。据此原则，我们把由动量方程的离散形式所规定的压力与速度的关系代入连续性方程的离散形式，从而得到压力修正方程，由压力修正方程得出压力修正值；接着，根据修正后的压力场求得新的速度场；然后，检查速度场是否收敛，若不收敛，则用修正后的压力值作为给定的压力场开始下一层次的计算，如此反复，直到获得收敛的解。

在上述求解过程中，如何获得压力修正值（即如何构造压力修正方程）以及如何根据压力修正值确定“正确”的速度（即如何构造速度修正方程），是SIMPLE算法的两个关键问题。为此，下面先解决这两个问题，然后给出SIMPLE算法的求解步骤。

（1）速度修正方程

考察一直角坐标系下的二维层流稳态问题。设有初始的猜测压力场p＊，我们知道，动量方程的离散方程可借助该压力场得以求解，从而求出相应的速度分量u＊和v＊。

根据动量方程的离散方程（7－32）和（7－38），有

现在，定义压力修正值p′为正确的压力场p与猜测的压力场p＊之差，有

p＝p＊＋p′　　（7－42）

同样地，定义速度修正值u′和v′，以联系正确的速度场（u，v）与猜测的速度场（u＊，v＊），有

u＝u＊＋u′　　（7－43）

v＝v＊＋v′　　（7－44）

将正确的压力场p代入动量方程的离散方程（7－32）与（7－38），得到正确的速度场（u，v）。现在，从方程（7－32）和（7－38）中减去方程（7－40）和（7－41），并假定源项b不变，有

引入压力修正值与速度修正值的表达式（7－42）至（7－44），方程（7－45）和（7－46）可写成

可以看出，由压力修正值p′可求出速度修正值（u′，v′）。式（7－48）还表明，任一点上速度的修正值由两部分组成：一部分是与该速度在同一方向上的相邻两节点间压力修正值之差，这是产生速度修正值的直接动力；另一部分是由相邻节点速度的修正值所引起的，这又可以视为四周压力的修正值对所讨论位置上速度改进的间接影响。

为了简化式（7－47）和（7－48）的求解过程，在此，引入如下近似处理：略去方程中与速度修正值相关的和该近似是SIMPLE算法的重要特征。这样处理后，对计算结果的精度并无影响。这是因为，如果保留，就必须用unb的相邻节点压力修正值和速度修正值表示这些项。这些邻点转而又引入邻点的邻点，如此等等。最后，速度修正公式将包含计算区域内所有节点的压力修正，这导致求解动量方程和连续性方程的完整方程组。略去，使我们能够把p′的方程写成通用微分方程的形式。因而可以利用逐次求解的过程，一次求解一个变量，实现了变量之间的解耦。等项代表着压力修正对速度的一种间接的、隐含的影响。计算实践已经证明，采用SIMPLE方法得出的收敛解，其压力场的解能使速度场（u＊，v＊）得到不断改进，最终满足连续性方程，略去等项不会导致任何误差。因为如果迭代趋于收敛，则u′趋于零，因而自然也应趋于零。于是有

以上两式中

将式（7－49）和式（7－50）所描述的速度修正值代入式（7－44）和式（7－45），有

对于ui＋1，J和vI，j＋1，存在类似的表达式

以上两式中

式（7－52）至式（7－56）表明，如果已知压力修正值p′，便可对猜测的速度场（u＊，v＊）作出相应的速度修正，得到正确的速度场（u，v）。

（2）压力修正方程

在上面的推导中只考虑了动量方程，其实，如前所述，速度场还受连续性方程的约束。按本节开头的约定，这里暂不讨论瞬态问题。对于稳态问题，连续性方程可写为

针对如图7－9所示的标量控制体积，连续性方程（7－57）满足如下离散形式

将正确的速度值，即式（7－52）—式（7－56），代入连续性方程的离散方程（7－58），有

图7－9　离散化的连续性方程的标量控制体积

整理后，得

该式可简记为

式中：

式（7－61）表示连续性方程的离散方程，即压力修正值p′的离散方程。方程中的源项b′是由于不正确的速度场（u＊，v＊）所导致的“连续性”不平衡量。通过求解方程（7－61），可得到空间所有位置的压力修正值p′。

如同处理式（7－36）中的密度一样，式（7－62）中的ρ是标量控制体积界面上的密度值，同样需要通过插值得到，这是因为密度ρ是在标量控制体积中的节点（即控制体积的中心）上定义和存储的，在标量控制体积界面上不存在可直接引用的值。无论采用何种插值方法，对于交界面所属的两个控制体积，必须采用同样的ρ值。

为了求解方程（7－61），还必须对压力修正值的边界条件作出说明。实际上，压力修正方程是动量方程和连续性方程的派生物，不是基本方程，故其边界条件也与动量方程的边界条件相联系。在一般的流场计算中，动量方程的边界条件通常有两类：第一，已知边界上的压力（速度未知）；第二，已知沿边界法向的速度分量。若已知边界压力p，可在该段边界上令p＊＝p，则该段边界上的压力修正值p′应为零。这类边界条件类似于热传导问题中已知温度的边界条件。若已知边界上的法向速度，在设计网格中，最好令控制体积的界面与边界相一致，这样，控制体积界面上的速度就为已知的。

（3）SIMPLE算法的计算步骤

至此，已经得出了求解速度分量和压力所需要的所有方程。根据前面介绍的SIMPLE算法的基本思想，可给出SIMPLE算法的计算流程，如图7－10所示。

图7－10　SIMPLE算法流程图

SIMPLE算法自问世以来，在被广泛应用的同时，也以不同方式不断地得到改善和发展，其中最著名的改进算法包括SIMPLEC、SIMPLER和PISO。限于篇幅，这里不再叙述，请读者查阅相关书籍。

7.1.4　商用CFD软件求解气相场的基本方法

7.1.4.1　常用的CFD软件

为了完成CFD计算，过去多是用户自己编写计算程序，但由于CFD的复杂性及计算机软硬件条件的多样性，使得用户各自的应用程序往往缺乏通用性，而CFD本身又有其鲜明的系统性和规律性，因此比较适合制作通用的商用CFD软件。自1981年以来，出现了如PHOENICS、CFX、STAR－CD、FIDAP、FLUENT等多个商用CFD软件，这些软件的显著特点是：

①功能比较全面，适用性强，几乎可以求解工程界中的各种复杂问题。

②具有比较易用的前、后处理系统和与其他CAD及CFD软件的接口能力，便于用户快速完成造型、网格划分等工作。同时，还可让用户扩展自己的开发模块。

③具有比较完备的容错机制和操作界面，稳定性高。

④可在多种计算机、多种操作系统，包括并行环境下运行。

随着计算机技术的快速发展，这些商用软件在工程界正在发挥着越来越大的作用。

（1）PHOENICS

PHOENICS是世界上第一套计算流体动力学与传热学的商用软件，它是“Parabolic Hyperbolic Or Elliptic Numerical Intergration Code Series”的缩写，由CFD的著名学者D.B.Spalding和S.V.Patankar等人提出，第一个正式版本于1981年开发完成。目前，PHOENICS主要由Concentration Heat And Momentum（CHAM）有限公司开发。

除了通用CFD软件应该拥有的功能外，PHOENICS软件有自己独特的功能：

①开放性。PHOENICS最大限度地向用户开放了程序，用户可以根据需要添加用户程序、用户模型。PLANT及In－Form功能的引入使用户不再需要编写Fortran源程序，GROUND程序功能使用户修改添加模型更加任意、方便。

②CAD接口。PHOENICS可以读入几乎任何CAD软件的图形文件。

③运动物体功能。利用MOVOBJ，可以定义物体运动，克服了使用相对运动方法的局限性。

④多种模型选择。提供了多种湍流模型、多相流模型、多流体模型、燃烧模型、辐射模型等。

⑤双重算法选择。既提供了欧拉算法，也提供了基于粒子运动轨迹的拉格朗日算法。

⑥多模块选择。PHOENICS提供了若干专用模块，用于特定领域的分析计算，如COFFUS用于煤粉锅炉炉膛燃烧模拟，FLAIR用于小区规划设计及高大空间建筑设计模拟，HOTBOX用于电子元器件散热模拟等。

PHOENICS的Windows版本使用Digital/Compaq Fortran编译器编译，用户的二次开发接口也通过该语言实现。此外，它还有Linux/Unix版本。其并行版本借助MPI或PVM在PC机群环境下及Compaq ES 40、HP K460、Silicon Graphics R10000（Origin）、Sun E450等并行机上运行。

访问http：//www.cham.co.uk和http：//www.phoenics.cn可以获得关于PHOENICS的详细信息及算例。

（2）CFX

CFX是第一个通过ISO　9001质量认证的商业CFD软件，由英国AEA　Technology公司开发。2003年，CFX被ANSYS收购。目前，CFX在航空航天、旋转机械、能源、石油化工、机械制造、汽车、生物技术、水处理、火灾安全、冶金、环保等领域有6000多个全球用户。

和大多数CFD软件不同的是，CFX除了可以使用有限体积法之外，还采用了基于有限元的有限体积法。基于有限元的有限体积法保证了在有限体积法的守恒特性的基础上，吸收了有限元法的数值精确性。在CFX中，基于有限元的有限体积法，对六面体网格单元采用24点插值，而单纯的有限体积法仅采用6点插值；对四面体网格单元采用60点插值，而单纯的有限体积法仅采用4点插值。在湍流模型的应用上，除了常用的湍流模型外，CFX最先使用了大涡模拟（LES）和分离涡模拟（DES）等高级湍流模型。

CFX是第一个发展和使用全隐式多网格耦合求解技术的商业化软件，这种求解技术避免了传统算法需要“假设压力项—求解—修正压力项”这样的反复迭代过程，而是同时求解动量方程和连续性方程，再加上其多重网格技术，CFX的计算速度和稳定性较传统方法提高了许多。此外，CFX的求解器在并行环境下获得了极好的可扩展性。CFX可运行于Unix、Linux、Windows平台。

CFX可计算的物理问题包括可压与不可压流动、耦合传热、热辐射、多相流、粒子输送过程、化学反应和燃烧等问题，还拥有诸如气蚀、凝固、沸腾、多孔介质、相间传质、非牛顿型流体、喷雾干燥、动静干涉、真实气体等大批复杂现象的实用模型。在其湍流模型中，纳入了k－ε模型、低雷诺数k－ε模型、低雷诺数Wilcox模型、代数雷诺应力模型、微分雷诺应力模型、微分雷诺通量模型、SST模型和大涡模型。

CFX为用户提供了CFX表达式语言（CEL）及用户子程序等不同层次的用户接口程序，允许用户加入自己的特殊物理模型。

CFX的前处理模块是ICEM　CFD，所提供的网格生成工具包括表面网格、六面体网格、四面体网格、棱柱体网格（边界层网格）、四面体与六面体混合网格、自动六面体网格、全局自动笛卡尔网格生成器等。它在生成网格时，可实现边界层网格自动加密、流场变化剧烈区域网格局部加密、分离流模拟等。

ICEM　CFD除了提供自己的实体建模工具之外，它的网格生成工具也可集成在CAD环境中。用户可在自己的CAD系统中进行ICEM　CFD的网格划分设置，如在CAD中选择面、线并分配网格大小属性等等。这些数据可储存在CAD的原始数据库中，用户在对几何模型进行修改时也不会丢失相关的ICEM　CFD设定信息。另外，CAD软件中的参数化几何造型工具可与ICEM CFD中的网格生成及网格优化等模块直接连接，大大缩短了几何模型变化之后的网格再生成时间。其接口适用于SolidWorks、CATIA、Pro/ENGINEER、I－DEAS、Unigraphics等CAD系统。

1995年，CFX收购了旋转机械领域著名的加拿大公司ASC，推出了专业的旋转机械设计与分析模块——CFX－TASCflow。CFX－TASCflow一直占据着旋转机械CFD市场的大量份额，是典型的气动/水动力学分析和设计工具。此外，它还有两个辅助分析工具：BladeGen和TurboGrid。BladeGen是交互式涡轮机械叶片设计工具，用户可以通过修改元件库存参数或完全依靠BladeGen中的工具设计各种旋转和静止叶片元件及新型叶片，对各种轴向流和径向流叶型，从CAD设计到CFD分析在数分钟内即可完成。TurboGrid是叶栅通道网格生成工具，它采用了创新性的网格模板技术，结合参数化能力，工程师可以快捷地为绝大多数叶片类型生成高质量叶栅通道网格。用户所需提供的只是叶片数目、叶片及轮毂和外罩的外形数据文件。

访问http：//www.ansys.com和http：//www.ansys.com.cn可以获得关于CFX及ICEM　CFD的详细信息及算例。

（3）STAR－CD

STAR－CD是由英国帝国理工学院提出的通用流体分析软件，由1987年在英国成立的CD－adapco集团公司开发。“STAR－CD”这一名称的前半段来自于“Simulation　of　Turbulent　flow in　Arbitrary　Regin”。该软件基于有限体积法，适用于不可压流和可压流（包括跨音速流和超音速流）的计算、热力学的计算及非牛顿型流体的计算。它具有前处理器、求解器、后处理器三大模块，以良好的可视化用户界面把建模、求解及后处理与全部的物理模型和算法结合在一个软件包中。

STAR－CD的前处理器（Prostar）具有较强的CAD建模功能，而且它与当前流行的CAD/CAE软件（SAMM、ICEM、PATRAN、I－DEAS、ANSYS、GAMBIT等）有良好的接口，可有效地进行数据交换。它具有多种网格划分技术（如Extrusion方法、Multi－block方法、Data　import方法等）和网格局部加密技术，具有对网格质量优劣的自我判断功能。Multi－block方法和任意交界面技术相结合，不仅能够大大简化网格生成，还能使不同部分的网格可以进行独立调整而不影响其他部分，可以求解任意复杂的几何形体，极大地增强了CFD作为设计工具的实用性和时效性。STAR－CD在适应复杂计算区域的能力方面具有一定优势。它可以处理滑移网格的问题，可用于多级透平机械内的流场计算。它提供了多种边界条件，可供用户根据不同的流动物理特性来选择合适的边界条件。它还提供了多种高级湍流模型，如各类k－ε模型。STAR－CD具有SIMPLE、SIMPISO和PISO等求解器，可根据网格质量的优劣和流动物理特性来选择。在差分格式方面，它具有低阶和高阶的差分格式，如一阶迎风、二阶迎风、中心差分、QUICK格式和混合格式等。

STAR－CD的后处理器具有动态和静态显示计算结果的功能，能用速度矢量图来显示流动特性，用等值线图或颜色来表示各个物理量的计算结果，可以进行气动力的计算。

STAR－CD在三大模块中提供了用户接口，用户可根据需要编制Fortran子程序并通过STAR－CD提供的接口函数来达到预期的目的。

访问http：//www.cd－adapco.com（或http：//www.cd.co.uk）和http：//www.cdaj－china.com可以获得关于STAR－CD的详细信息及算例。

（4）FIDAP

FIDAP是由英国Fluid　Dynamics　Internationa（FDI）公司开发的计算流体力学与数值传热学软件。1996年，FDI被FLUENT公司收购，这样，目前的FIDAP是属于FLUENT公司的一个CFD软件。

与其他CFD软件不同的是，该软件完全基于有限元法。FIDAP可用于求解聚合物、薄膜涂镀、生物医学、半导体晶体生长、冶金、玻璃加工以及其他领域中出现的各种层流和湍流的问题。它对涉及流体流动、传热、传质、离散相流动、自由表面、液固相变、流固耦合等的问题都提供了精确而有效的解决方案。在采用完全非结构网格时，全耦合、非耦合及迭代数值算法都是可以选择的。FIDAP提供了广泛的物理模型，不仅可以模拟非牛顿型流体流变学、辐射传热、多孔介质中流动，而且对于质量源项、化学反应及其他复杂现象都可以精确模拟。

在网格处理方面，它提供了四边形、三角形、六面体、四面体、三角柱和混合单元网格。它可导入I－DEAS、PSTRAN、ANSYS和ICEM　CFD等软件所生成的网格模型。

FIDAP在求解器方面，可利用完全非结构网格，采用有限元法求解所有速度范围内的问题。对于瞬态问题，它提供显式和隐式两种时间积分方案。它利用牛顿－拉夫逊迭代法、修正的牛顿法、Broyden更新的牛顿法等来解方程组。

它具有自由表面模型功能，可同时使用变形网格和固定网格，从而模拟液汽界面的蒸发与冷凝相变现象、流面晃动、材料填充等。

它所提供的流固耦合分析功能，可使固体结构中的变形和应力与流体流动、传热和传质耦合计算。其中，变形结构和流体域的网格重新划分是使用弹性网格重新划分体系完成的。

它提供的湍流模型包括代数混合长度模型和k‐ε模型等。提供了用户接口，让用户自己定义连续性方程、动量方程、能量方程及组分方程中特定的体积源项，定义标量输运方程，定制后处理量等。其后处理功能可输出ANSYS格式的计算结果。

访问http：//www.ansys.com及http：//www.hikeytech.com可获取关于FIDAP软件的详细信息及算例。

（5）FLUENT

FLUENT是由美国FLUENT公司于1983推出的CFD软件。它是继PHOENICS之后的第二个投放市场的基于有限体积法的软件。FLUENT是目前功能最全面、适用范围最广、国内使用最广泛的CFD软件之一。下一小节将对这一软件的基本理论及使用方法进行介绍。

7.1.4.2　FLUENT简介

FLUENT是用于计算流体流动和传热问题的软件。它提供的非结构网格生成程序对相对复杂的几何结构网格生成非常有效，可以生成的网格包括二维的三角形和四边形网格，三维的四面体、六面体及混合网格。FLUENT还可根据计算结果调整网格，这种网格的自适应能力对于精确求解有较大梯度的流场有很实际的作用。由于网格自适应和调整只是在需要加密的流动区域里实施，而非整个流场，因此可以节约计算时间。

1）FLUENT软件的结构

FLUENT软件包由以下几个部分组成：

（1）GAMBIT——用于建立几何结构和生成网格。

（2）FLUENT——是用于进行流动模拟计算的求解器。

（3）prePDF——用于模拟PDF燃烧过程。

（4）TGrid——用于从现有的边界网格生成体网格。

（5）Filters（Translators）——转换其他程序生成的网格，用于FLUENT计算。

可以接口的程序包括：ANSYS，I－DEAS，NASTRAN，PATRAN等。

利用FLUENT软件进行流体流动与传热的模拟计算流程如图7－11所示。首先，利用GAMBIT进行流动区域几何形状的构建、边界类型以及网格的生成，并输出用于FLUENT求解器计算的格式；然后，利用FLUENT求解器对流动区域进行求解计算，并进行计算结果的后处理。

图7－11　FLUENT基本程序结构示意图

2）FLUENT软件可以求解的问题

FLUENT可以采用三角形、四边形、四面体、六面体及其混合网格，其基本控制体形状如图7－12所示。FLUENT可以计算二维和三维流动问题，在计算过程中，网格可以自适应调整。FLUENT软件的应用范围非常广泛，主要范围如下：

图7－12　FLUENT的基本控制体形状

（1）可压缩与不可压缩流动问题。

（2）稳态和瞬态流动问题。

（3）无粘流、层流及湍流问题。

（4）牛顿型流体及非牛顿型流体。

（5）对流换热问题（包括自然对流和混合对流）。

（6）导热与对流换热耦合问题。

（7）辐射换热。

（8）惯性坐标系和非惯性坐标系下的流动问题模拟。

（9）用拉格朗日轨道模型模拟稀疏相（颗粒、水滴、气泡等）。

（10）一维风扇、热交换器性能计算。

（11）两相流问题。

（12）复杂表面形状下的自由面流动问题。

3）用FLUENT软件求解问题的步骤

利用FLUENT进行求解的步骤如下：

（1）确定几何形状，生成计算网格（用GAMBIT，也可以读入其他指定程序生成的网格）。

（2）输入并检查网格。

（3）选择求解器（2D或3D等）。

（4）选择求解的方程：层流或湍流（或无粘流）、化学组分或化学反应、传热模型等；确定其他需要的模型，如风扇、热交换器、多孔介质等模型。

（5）确定流体的材料物性。

（6）确定边界类型及其边界条件。

（7）条件计算控制参数。

（8）流场初始化。

（9）求解计算。

（10）保存结果，进行后处理等。

4）关于FLUENT求解器的说明

（1）FLUENT　2d——二维单精度求解器。

（2）FLUENT　3d——三维单精度求解器。

（3）FLUENT　2ddp——二维双精度求解器。

（4）FLUENT　3ddp——三维双精度求解器。

5）FLUENT求解方法的选择

FLUENT的求解方法包括：非耦合求解方法、耦合隐式求解方法、耦合显式求解方法。

非耦合求解方法主要用于不可压缩或低马赫数压缩性流体的流动。耦合求解方法则可以用在高速可压缩流动。FLUENT的默认设置是非耦合求解，但对于高速可压缩流动，或需要考虑体积力（浮力或离心力）的流动，求解问题时网格要比较密，因此建议采用耦合隐式求解方法求解能量和动量方程，可较快地得到收敛解，而其缺点是需要的内存比较大（是非耦合求解方法的迭代时间的1.5～2.0倍）。如果必须要耦合求解，但机器内存不够时，可以考虑用耦合显式解法器求解问题。该解法器也耦合了动量、能量及组分方程，但内存却比隐式求解方法小，而其缺点是收敛时间比较长。

6）边界条件的确定

利用FLUENT软件包进行计算的过程中，边界条件的正确设置是关键的一步。设置边界条件的方法一般是在利用GAMBIT建模的过程中设定的，也可以在FLUENT求解器中对边界类型进行重新设定。

FLUENT软件提供了十余种类型的进、出口边界条件，分别介绍如下。

（1）速度入口（velocity－inlet）

给定入口边界上的速度及其他相关标量值。该边界条件适用于不可压缩流动问题，对可压缩流动问题则不适合，否则该入口边界条件会使入口处的总温或总压有一定的波动。

速度入口边界条件设置对话框如图7－13所示，输入量包括：速度大小、方向或各速度分量、周向速度（轴对称有旋流动）、静温（考虑能量）等。

图7－13　速度入口边界设置对话框

（2）压力入口（pressure－inlet）

给出入口边界上的总压。压力入口边界条件通常用于流体在入口处的压力为已知的情形，对计算可压缩和不可压缩流动问题都适合。压力入口边界条件通常用于入口处的流量或流动速度为未知时的流动。压力入口边界条件还可以用于处理自由边界问题。

压力入口边界的设置对话框如图7－14所示，其中第一项的表压强与绝对压强、操作压强有如下的关系

另外还应注意，这里给出的表压强的大小是入口边界上的总压。对于不可压缩流动，有

图7－14　压力入口边界设置对话框

对于可压缩流动，有

压力入口边界条件设置需要输入的参数有总压、总温、流动方向、静压、湍流量（用于湍流计算）、辐射参数（考虑辐射）、化学组分质量分数（考虑化学组分）、混合分数及其方差（用PDF燃烧模型）、进度变量（progress　variable）（预混燃烧计算）、离散相边界条件（稀疏相计算）及第二相体积分数（多相计算）等。

（3）质量入口（mass－flow－inlet）

质量入口边界条件主要用于可压缩流动，对于不可压缩流动，由于密度是常数，可以采用速度入口边界条件。

质量入口边界条件包括两种：质量流量和质量通量。质量流量是单位时间内通过入口总面积的质量。质量通量是单位时间单位面积内通过的质量。如果是二维轴对称问题，质量流量是单位时间内通过2π弧度的质量，而质量通量是单位时间内通过1弧度的质量。

给定入口边界上的质量流量，此时局部入口总压是变化的，用以调节速度，从而达到给定的流量，这使得计算的收敛速度变慢。所以，如果压力边界条件和质量边界条件都适用时，应优先选择用压力入口边界条件。对于不可压缩流动，由于密度是常数，可以选择采用速度入口边界条件。

（4）压力出口（pressure－outlet）

对于有回流的出口，可给定出口边界上的静压（表压），该边界条件比下文的自由出流（outflow）边界条件更容易收敛。该边界条件只能用于模拟亚音速流动。如果当地速度已经超过音速，该压力在计算过程中就不应采用了，而应根据内部流动计算结果给定压力。其他量都是根据内部流动外推出边界条件。该边界条件可以处理出口有回流的问题，合理地给定出口回流条件，有利于解决有回流出口问题的收敛困难。

出口回流条件需要给定：回流总温（如果有能量方程）、湍流参数（湍流计算）、回流组分质量分数（有限速率模型模拟组分输运）、混合物质量分数及其方差（PDF计算燃烧）。如果有回流出现，给定的表压将被视为总压，所以不必给出回流压力。回流流动方向与出口边界垂直。

在出口压力边界条件给定中，需要给定出口静压（表压）。当然，该压力只用于亚音速计算。如果局部变成超音速，则根据前面的来流条件外推出口边界条件。需要特别指出的是，这里的压力是相对于前面给定的工作压力。

（5）无穷远压力边界（pressure－far－field）

如果知道来流的静压和马赫数，FLUENT提供了无穷远压力边界条件来模拟该类问题。该边界条件用于可压缩流动，适用于用理想气体定律计算密度的问题。为了满足无穷远压力边界条件，需要把边界放到离我们关心的区域足够远的地方。

给定边界静压、温度及马赫数，可以是亚音速、跨音速或者超音速，并且需要给定流动方向，如果有需要还必须给定湍流量等参数。

无穷远压力边界条件是一种不反射边界条件。

（6）自由出流（outflow）

对于出流边界上的压力或速度均为未知的情形，可以选择自由出流边界条件。

这类边界条件的特点是不需要给定出口条件（除非是计算分离质量流、辐射换热或者包括颗粒稀疏相的问题），出口条件都是通过FLUENT内部计算得到。但并不是所有问题都适合，如下列情况就不能用自由出流边界条件：

①包含压力进口条件；

②可压缩流动问题；

③有密度变化的非稳定流动问题（即使是不可压缩流动）。

采用自由出流边界条件时，所有变量在出口处的扩散通量为零，即出口平面是从前面的结果计算得到并且对上游没有影响。计算时，如果出口截面通道大小没有变化，应采用完全发展流动假设。当然，在径向是允许有梯度存在时，只是假定在垂直出口截面方向上扩散通量为零。

（7）进口通风（inlet　vent）

进口通风边界条件需要给定入口损失系数、流动方向以及进口环境总压和总温。

对于进口通风模型，假定进口风扇无限薄，通风压降正比于流体动压头和用户提供的损失系数。再假定ρ是流体密度，KL是无量纲损失系数，则压降为

其中，v是与通风方向垂直的速度分量，Δp是流动方向上的压降。

（8）进口风扇（intake fan）

进口风扇边界条件需要给定压降、流动方向和环境总压和总温。

假定进口风扇无限薄并且有不连续的压力升高，压力升高量是流体通过风扇的速度的函数。如果是反向流动，风扇可被看作通风出口并且损失系数为1。

压力阶跃可以是常数或者是流动方向的垂直方向上速度分量的函数形式。

（9）出口通风（outlet vent）

出口通风边界条件用于模拟出口通风情况，并给定一个损失系数以及环境（出口）压力和温度。

出口通风边界条件需要给定的参数包括：静压、回流条件、辐射参数、离散相边界条件、损失系数。

（10）排气扇（exhaust fan）

排气扇边界条件用于模拟外部排气扇，给定一个压升和环境压力。

假定排气扇无限薄，并且流体通过排气扇的压升是流体速度的函数。

（11）对称边界（symmetry）

对称边界条件适用于流动及传热场是对称的情形。在对称轴或者对称平面（如图7－15）上，既无质量的交换也无热量等其他物理量的交换，因此垂直于对称轴或者对称平面的速度分量为零。在对称轴或者对称平面上，所有物理量在其垂直方向上的梯度为零，因此在对称边界上，垂直于边界的速度分量为零，任何量的梯度也为零。

计算中不需要给定任何参数，只需要确定合理的对称位置。该边界条件可用于黏性流动中运动边界的处理。

图7－15　对称面示意图

图7－16　周期性边界示意图

（12）周期性边界（periodic）

如果我们关心的流动，其几何边界上的流动和换热是周期性重复的，那么可以采用周期性边界条件。周期性边界示意图如图7－16所示。FLUENT提供了两种类型的周期性边界条件：一类是流体经过周期性重复后没有压降（cyclic），另外一类有压降（periodic）。

（13）固壁边界（wall）

对于黏性流动问题，FLUENT的默认设置是壁面无滑移条件。对于壁面有平移运动或者旋转运动的情况，可以指定壁面切向速度分量，也可以给出壁面切应力从而模拟壁面滑移。根据流动情况，可以计算壁面切应力和与流体换热情况。壁面热边界条件包括固定热通量、固定温度、对流换热系数、外部辐射换热与对流换热等。

如果给定壁面温度，则壁面向流体的换热量为

向固体壁面的换热量为

如果给定热通量，则根据流体换热和固体换热量计算出的壁面温度分别为

如果是对流换热边界条件（给定对流换热系数hext），则

如果是辐射换热边界条件，给定辐射系数εext，则

如果同时考虑对流和辐射，则

流体侧的换热系数根据如下公式计算：

7.1.4.3　FLUENT实例操作步骤

长期以来，流化床被广泛应用于各种工业过程中，气固两相在流化床中的浓度分布以及压降等问题一直是研究的热点，而FLUENT中的欧拉（Eulerian）模型提供了一个很实用的工具来研究涉及复杂相间动量交换的稠密气固两相流动。

如图7－17所示，流化床的尺寸为1m×0.15m，入口空气速度为1.5m/s，初始状态下，底部堆积着高度为0.5m的颗粒，固相容积份额为0.55，上部为空气。

1）利用GAMBIT建立计算区域和边界条件

（1）步骤1：文件的创建

双击GAMBIT的快捷方式图标，可以打开如图7－18所示的对话框，“Working　Directory”为工作目录及GAMBIT相关文档的保存目录。可以通过单击图中的“Browse”按钮进行更换。

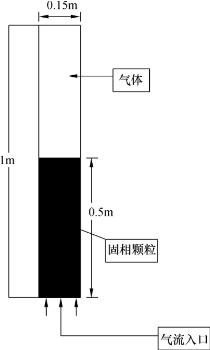
图7－17　流化床结构模型

图7－18　GAMBIT启动对话框

单击“Run”按钮，启动GAMBIT之后的窗口布局如图7－19所示。

图7－19　GAMBIT的操作界面

（2）步骤2：创建面

依次点击“Operation”区域的 →“Geometry”区域的 →“Face”区域的 ，打开“Create　Real　Rectangular　Face（创建矩形面）”面板，如图7－20所示。将图中的“Width”和“Height”分别设置为“0.15”和“1”，点击“Apply”按钮即可创建流化床的计算区域，此时可以点击屏幕右下方（如图7－19所示）的“Global Control”区域的 ，使所建图形在显示区域中以全图显示，见图7－21。

图7－20　“Create Real Rectangular Face”面板

图7－21　面的创建

（3）步骤3：网格划分

依次点击“Operation”区域的 →“Mesh”区域的 →“Face”区域的 ，打开“Mesh　Faces”面板，如图7－22所示，对面直接进行划分。在图中的“Faces”选项框中选中要操作的面，然后设定“Spacing”设置区中的数值为“0.005”，要注意的是数字右边的项目是“Interval　size”，其余选项保持默认设置，最后单击左下侧的“Apply”按钮，可以看到如图7－23所示的面的网格划分。

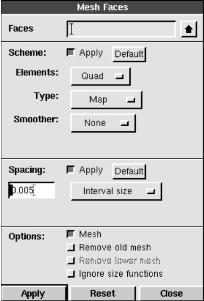
图7－22　“Mesh Faces”面板

图7－23　面的网格划分

（4）步骤4：边界条件的指定

依次点击“Operation”区域的 →“Zones”区域的 ，打开“Specify Boundary Types”面板，如图7－24所示，指定边界条件的类型。在图中的“Name”文本框填写入口边界的名称为“Inlet”，“Type”设置区中选择速度入口“VELOCITY－INLET”。图中“Entity”设置区表示的是即将对哪个实体进行边界条件设定，本例中保持缺省设置为“Edges”，单击其右侧的黄色选项框，按住“Shift”键的同时单击绘图界面中的下侧入口边界，此时黄色选项框中将出现入口边界所对应的边“edge.1”，最后点击“Apply”按钮，完成入口边界条件的设置。同理可将出口边界（edge.3）设置为自由出流边界“OUTFLOW”并将其取名为“Outlet”。

图7－24　边界条件的设定

（5）步骤5：Mesh网格文件的输出

依次点击“File”→“Export”→“Mesh”，打开了输出文件对话框，如图7－25所示。要指出的是，本例为二维情况，需选中对话框下方的“Export 2－D（X－Y）Mesh”复选框，才能正确输出Mesh文件。可将网格文件命名为“FB”，最后点击“Aplly”按钮，就可以输出FLUENT求解器使用的.msh文件了。

图7－25　网格文件输出对话框

2）利用FLUENT求解流场

利用GAMBIT建立计算区域、划分网格、指定边界条件和输出Mesh文件后，就可以利用FLUENT导入所生成的Mesh文件，并对相应问题进行求解。

（1）步骤1：FLUENT求解器的选择

双击FLUENT的快捷方式图标，就可以开启如图7－26所示的对话框，要求用户选择FLUENT求解器的版本类型。“2d”表示二维、单精度求解器，“2ddp”为二维双精度求解器，“3d”和“3ddp”表示三维求解器。本例是二维情况并且对求解的精度要求不高，所以选择二维单精度求解器即可，单击“Run”按钮，启动FLUENT求解器。

FLUENT求解器启动后，会出现如图7－27所示的操作界面，菜单栏集中了FLUENT中的常用功能，控制台窗口是FLUENT所有命令发出和显示的地方。

图7－26　FLUENT版本选择对话框

图7－27　FLUENT操作界面

（2）步骤2：网格文件的导入及设置

①读入网格文件。

依次点击“File”→“Read”→“Case...”，打开如图7－28所示的网格文件导入对话框，找到前面所生成的FB.msh网格文件，单击“OK”按钮，即可导入网格文件。

图7－28　网格文件导入对话框

②检查网格文件。

依次点击“Grid”→“Check”，可获得网格信息，如图7－29所示。需要注意的是，从网格信息中的“minimum volume”部分可以知道最小的网格体积，必须保证其值大于0，若为负数，则必须重新划分网格。

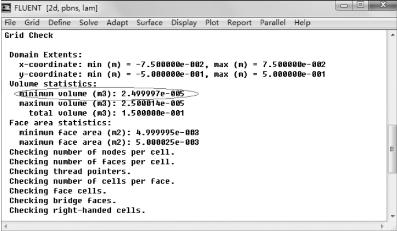
图7－29　检查网格的信息反馈

③设置计算区域尺寸。

依次点击“Grid”→“Scale...”，打开如图7－30所示的“Scale Grid”对话框。FLUENT中默认的长度单位为m，但有些情况下，为了GAMBIT作图时的方便，常常使用mm、cm等其他单位，这时我们就可以通过“Scale Grid”对话框对计算区域进行缩放。调整“Scale Factors”设置区中“X”、“Y”的比例，或者通过“Grid Was Created In”下拉列表框选择网格创建时使用的单位后，单击下方的“Scale”按钮即可。

在本例中，流化床的尺寸为1m×0.15m，而在GAMBIT创建面时所建矩形面的尺寸的“Width”和“Height”分别设置为“0.15”和“1”（参见图7－20），由此可知计算区域尺寸单位为m，因此无需对计算区域进行缩放，保持如图7－30所示的默认设置即可，最后单击“Close”按钮关闭当前对话框。

④显示网格。

依次点击“Display”→“Grid...”，打开如图7－31所示的“Grid Display（网格显示）”对话框。选中“Surfaces”列表框中的所有界面，单击“Display”按钮，会弹出一个新的图形窗口，在此窗口中就会看到如图7－32所示的网格形状。

图7－30　“Scale Grid”对话框

图7－31　“Grid Display”对话框

图7－32网格图

（3）步骤3：选择计算模型

①求解器的定义。

依次点击“Define”→“Models”→“Solver...”，打开如图7－33所示的“Solver”对话框来定制求解器的类型。在“Time”选项框中选择“Unsteady”，表示为非稳态计算，其余保持默认设置，然后点击“OK”按钮关闭当前对话框。

图7－33　“Solver”对话框

②多相流模型的选择。

依次点击“Define”→“Models”→“Multiphase...”，打开设置多相流模型的“Multiphase Model”对话框，见图7－34。在“Model”选项框中选择“Eulerian”，右侧的“Number of Phases”文本框中可以设置相的个数。设置好后点击“OK”按钮关闭当前对话框。

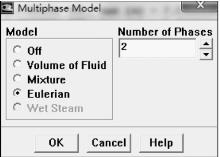
图7－34　“Multiphase Model”对话框

图7－35　“Viscous Model”对话框

③选用湍流模型。

依次点击Define→Models→Viscous...，打开如图7－35所示的“Viscous Model”对话框，选中“k－epsilon（2eqn）”单选按钮后对话框展开如图7－36所示，保持所有的默认设置，点击“OK”按钮接受并关闭当前对话框。

图7－36　“Viscous Model”展开对话框

（4）步骤4：定义流体的物理性质

依次点击“Define”→“Materials...”，打开“Materials”对话框，如图7－37所示，可以设置空气的密度（Density）和动力粘度（Viscosity），本例中保持默认设置，这样气相的物理性质就定义完毕。接下来，再定义固相的物理性质，在图7－37的“Name”文本框中将名称改为“solids”，密度设为“2 500”kg/m3，粘度为“10”kg/（m·s）。然后点击“Change/Create”按钮，弹出如图7－28所示的提示对话框，点击“No”按钮。此时，“Materials”对话框的“Fluent Fluid Materials”下拉列表框中多了“solids”选项，选中该选项后出现如图7－39所示的对话框，这样固相就创建完成了。

图7－37　气相物性设置对话框

图7－38　提示对话框

图7－39　固相物性设置对话框

（5）步骤5：相设置

依次点击“Define”→“Phase...”，打开“Phases”对话框，如图7－40所示。本例中包含两相：基本相和第二相，具体设置如下：

①基本相的设定。

在“Phases”对话框的“Phase”选项框中选中“phase－1”，在“Type”选项框中选中“primary－phase”，然后单击“Set...”按钮，打开如图7－41所示的“Primary Phase”对话框。在“Name”文本框中输入“air”代替原来的phase－1，在“Phase Material”下拉列表框中选择“air”，最后单击“OK”按钮，即定义了air为基本相。

图7－40　“Phases”对话框

图7－41　气相设置对话框

②第二相的设定。

在图7－40的对话框中选中“phase－2”，在“Type”选项框中选中“secondary－phase”，点击“Set...”按钮，打开如图7－42所示的“Secondary Phase”对话框。在“Name”文本框中输入“solid”代替原来的phase－2，在“Phase Material”下拉列表框中选择“solids”，选中“Granular”复选框，在“Diameter”设置区的文本框中输入“0.000 3”，“Granular Viscosity”下拉列表框中选择“syamlal－obrien”，其他保持默认设置。最后单击“OK”按钮，即定义了solid为第二相，结果如图7－43所示。

图7－42　固相设置对话框

图7－43　相的设定结果

点击图7－43中的“Interaction...”按钮，打开“Phase Interaction”对话框，如图7－44所示，在此可以对相间曳力、升力以及固相间的碰撞恢复系数等参数进行设置。本例中保持默认设置。

图7－44　气固两相间相互作用参数设置

（6）步骤6：操作环境的设置

依次点击“Define”→“Operation Condition...”，打开“Operation Conditions”对话框，如图7－45所示，选中“Gravity（重力）”复选框，指定重力方向，由于本例中重力指向y轴的负方向，因此在“Y（m/s2）”文本框中输入重力加速度“－9.81”。

同时，将“Specified Operating Density”复选框选中，并接受默认的值“1.225”。

图7－45　“Operating Conditions”对话框

（7）步骤7：边界条件的设置

依次点击“Define”→“Boundary Conditions...”，打开如图7－46所示的“Boundary Conditions”对话框。在“Zone”列表框中选中“inlet”，并在“Phase”下拉列表框中选中“air”，点击“Set...”按钮，打开“Velocity Inlet”对话框，如图7－47所示。速度大小“Velocity Magnitude”设为“1.5m/s”，点击“OK”按钮。再在图7－46的“Phase”下拉列表框中选中“solid”，打开“Velocity Inlet”对话框，点击“Multiphase”选项卡，如图7－48所示，在“Volume Fraction”文本框中设置入口固相介质的容积份额为“0”。

此外，本例中出口边界条件保持默认设置即可。

图7－46　“Boundary Conditions”对话框

图7－47　“Velocity Inlet”对话框

图7－48　入口固相浓度设置

（8）步骤8：求解控制器的设置

依次点击“Solve”→“Controls”→“Solution...”，打开“Solution Controls”对话框，如图7－49所示。将“Equtions”列表框中的求解方程全部选中，在“Pressure－Velocity Coupling”下拉列表框中选择“Phase Coupled SIMPLE”，即采用相间耦合的SIMPLE算法，“Under－Relaxation Factors（欠松弛因子）”设置区保持默认设置，“Discretization（离散化方法）”设置区中均采用“First Order Upwind（一阶迎风格式）”。

图7－49　“Solution Controls”对话框

（9）步骤9：初始化

①全场初始化。

依次点击“Solve”→“Initialize”→“Initialize...”，打开“Solution Initialization”对话框，在“Compute From”下拉列表框中选择“inlet”，其余保持默认设置，点击“Init”按钮初始化全场，如图7－50所示。

图7－50　“Solution Initialization”对话框

②固相区域初始化。

本例中，由于初始状态下流化床的下半部分为固相，因此还需对该区域的固相容积份额进行初始化。

首先定义一个区域。依次点击“Adapt”→“Region...”，打开如图7－51所示的“Region Adaption”对话框，分别设置“X Min”“Y Min”为“－0.075”“－0.5”，“X Max”“Y Max”为“0.075”“0”，然后单击“Mark”按钮创建一个临时寄存器定义底部固相区域。如果继续点击图7－51的“Manage...”按钮会弹出如图7－52所示的“Manage Adaption Registers”对话框，可以看到有一个寄存器（Registers）“hexahedron－r0”，右侧有该寄存器的信息，表示定义成功，点击“Close”按钮关闭对话框即可。

接下来将流化床下部初始化为固相。依次点击“Solve”→“Initialize”→“Patch...”，打开如图7－53所示的“Patch”对话框。在“Phase”下拉列表框中选择“solid”，在“Variable”列表框中选择“Volume Fraction”，“Registers to Patch”列表框中选择“hexahedron－r0”，然后在“Value”文本框中输入“0.55”，最后单击“Patch”按钮，固相区域初始化完成。

图7－51　“Region Adaption”对话框

图7－52　“Manage Adaption Registers”对话框

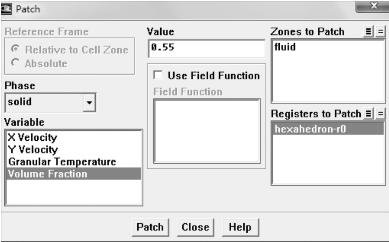
图7－53　“Patch”对话框

（10）步骤10：设置残差监视器

依次点击“Solve”→“Monitors”→“Residual...”，打开“Residual Monitors”对话框，如图7－54所示。在“Options”选项组中选中“Plot”，这样可以在迭代过程中绘制各守恒方程的残差。为了使迭代过程中的图像显示窗口与残差监视器窗口不发生冲突，将“Plotting”选项组的“Window”调为“1”，其余保持默认值，单击“OK”按钮即可。

图7－54　“Residual Monitors”对话框

（11）步骤11：动画记录

依次点击“Solve”→“Animate”→“Define...”，打开如图7－55所示的“Solution Animation”对话框。单击“Animation Sequence”选项框右边的向上箭头，即增加1个动画记录，此时下方出现一个高亮显示的行，在“Name”文本框中输入“ms”，“When”下选择“Time　Step”，“Every”文本框中输入“10”，即每计算10个时间步长记录一次图片，再单击后面的“Define...”按钮，打开“Animation Sequence”对话框，如图7－56所示。在“Storage　Type”选项组中选中“PPM　Image”，在“Storage　Directory”文本框中输入图片保存路径，在“Display Type”选项组中选中“Contours”，出现“Contours”对话框，如图7－57所示。在“Options”选项组中勾选“Filled”复选框，在“Contours of”下拉列表框中选择“Phases...”，在“Phase”下拉列表框中选择“solid”，其余保持不变，单击“Display”按钮，弹出的图形窗口显示了计算区域初始的相分布，如图7－58所示。

图7－55　“Solution Animation”对话框

图7－56　“Animation Sequence”对话框

图7－57　“Contours”对话框

图7－58　初始时刻固相的体积分数云图

单击“Close”关闭“Contours”对话框，再单击“OK”按钮关闭“Animation Sequence”对话框，最后点击“OK”按钮关闭“Solution Animation”对话框。

（12）步骤12：保存文件

依次点击“File”→“Write”→“Autosave...”，

打开如图7－59所示的“Autosave Case/Data”对话框。在“Autosave Case File Frequency”和“Autosave Data File Frequency”文本框中均输入“100”，表示每计算100个时间步长自动保存一次Case和Data文件，最后点击“OK”按钮关闭对话框。

图7－59　“Autosave Case/Data”对话框

（13）步骤13：迭代计算

依次点击“Solve”→“Iterate...”，打开如图7－60所示的“Iterate”对话框。在“Time Step Size（s）”文本框中输入“0.001”，“Number of Time Steps”文本框中输入“8　000”，即该工况模拟的总时间为8s，在“Max Iteration per Time Step”文本框中输入“20”，其余保持默认值。单击“Iterate”按钮开始迭代计算。

（14）步骤14：结果后处理

迭代计算完成后，读取不同时刻的Case和Data文件，然后依次点击“Display”→“Contours...”，打开“Contours”对话框（如图7－57所示），在“Options”选项组中勾选“Filled”复选框。在“Contours of”下拉列表框中选择“Phases...”，在“Phase”下拉列表框中选择“solid”，其余保持不变，单击“Display”按钮，弹出的图形窗口显示了不同时刻计算区域固相浓度的分布，如图7－61所示。

图7－60　“Iterate”对话框

图7－61　不同时刻固相的体积分数云图

7.2　基于拉格朗日框架下的固相求解

7.2.1　求解方法

通过第4章的学习，我们已经对离散颗粒在气流中的受力方程有了整体认识，而本节将示范在拉格朗日框架下，如何通过颗粒的受力分析求解出运动方程，包括颗粒的加速度、速度以及位移。

首先，我们来看一下颗粒的线性运动方程

F＝mdv/dt　　　（7－75）

将此方程重写成下面的形式，让它能被积分

dv/dt＝F/m　　（7－76）

这个方程可以这么解释：速度上无穷小的变化量dv等于（F/m）乘以时间无穷小的变化量。取时间的有限间隔，因此无限小的dt变成离散的时间增量Δt，并得到离散的速度改变量Δv为

这个公式计算的不是瞬间速度，而是速度改变量的估计值。所以要估计颗粒的实际速度，必须要知道时间变量Δt之前的速度。也就是在模拟开始时（当时间为0），需先知道颗粒的初速度，这被称为初始状态。当使用以下的方程计算颗粒在不同时间的速度时，此初始状态是必需的

其中的初始状态是

式中，vt是在时间t时的速度，vt＋Δt是时间t时加上某个时间间隔时的速度，Δt代表时间间隔，而v0是时间为0时的初速度。

利用线性运动方程积分来估计颗粒的位移（或位置）。当算出新的速度后，可用以下公式估计在时间t＋Δt时的位移

其中位移的初始状态是

需要指出的是，时间间隔越小时（也就是说Δt越接近dt），求出来的值越精确。然而，使用越小的时间间隔，则计算所花费的CPU时间越长。

7.2.2　实例分析

下面将结合简单范例来说明固相运动的求解方法。

例7－1　有一质量为1kg的圆球，从高度y＝150m处，以10m/s的初速度水平向右抛出，假设运动过程中圆球仅受到重力，求：该圆球在抛出后0－5s内的运动轨迹。

本例中，圆球的初始位置为

圆球的初速度为

现采用上述的欧拉积分法对圆球的速度进行求解，即

本例中，由于圆球仅受到y方向的重力，因此上式在x方向以及y方向的速度表达式可分别写为

其中，g＝－9.81m/s2，Δt＝0.001s，再利用下式计算在时间t＋Δt时的位移

图7－62为本例的数值模拟结果，当t＝5s时，x＝49.999　9，y＝27.350　5。而根据牛顿第二定律可以得知，本例中圆球在t＝5s时，精确解应为x＊＝50，y＊＝27.375，数值模拟的最大误差仅约为0.09%。

图7－62　小球的运动轨迹

7.3　气固两相间的单向耦合与双向耦合

图7－63　气固双向耦合求解流程图

上两个小节已分别针对气相场和固相的求解方法进行了介绍，在联合运用欧拉方法和拉格朗日方法处理气相和离散颗粒相时，涉及单向耦合与双向耦合的问题。在计算过程中，如果仅考虑气相场对固相场的影响，而不考虑固相场对气相场的影响，则称为单项耦合；如果既考虑气相场对固相场的影响，又同时考虑固相场对气相场的影响，则称为双向耦合。显然，双向耦合比单相耦合具有更高的准确性，但数学模型相对复杂。下面将举例说明联合运用欧拉－拉格朗日方法进行气固两相流动双向耦合的求解，其计算流程图可参见图7－63。

（1）气相流场、颗粒场初始化。

（2）采用SIMPLE等方法在给定的时间步长内进行数值计算以求解两相耦合的纳维－斯托克斯方程，获取气相速度场。

（3）求解颗粒运动：分别求解气相－固相作用力以及固相－固相之间的作用力，从而确定固相所受的合力及加速度。采用欧拉积分法计算全部颗粒经过一个时间步长后的位置和速度，以确定颗粒的运动轨迹。

（4）统计、更新气相流场网格内的空隙率，并计算网格内颗粒平均速度，然后计算颗粒对流场的反作用源项。

（5）修正两相耦合的纳维－斯托克斯方程，得出新的气相流场。

（6）重复（2）－（5）步。

图7－64为循环流化床脱硫塔中颗粒场分布随时间变化的数值模拟结果，其中（a）组图采用的是气固单向耦合计算方法，而（b）组图则采用的是双向耦合的计算方法。由（a）、（b）两组图的对比可以看出，气固单向耦合与双向耦合的计算结果有着较为明显的区别，双向耦合的计算精度相对更高，所获得的计算结果更加接近实际，然而花费的计算时间也较多。

图7－64　气固单向及双向耦合数值模拟结果的对比

7.4　后处理方法

7.4.1　数据的存储与读取

为了在气固两相数值计算后期可以随时调用某一时刻的计算结果，我们需要在数值计算过程中保存相应的气相及固相的流动数据，例如气体速度以及颗粒的位置、尺寸、速度等参数。数据存储的频率应根据使用者后期结果分析的需要以及计算机的硬件条件进行设定。一般情况下，气固两相流动每进行0.1s，至少需要存储1次数据。下面将结合Visual Basic中顺序文件的操作方法，介绍如何对数据文件进行存储及读取。

Visual Basic中的顺序文件是普通的文本文件，是一种结构比较简单的文件格式。它的存储方式是顺序存储，即数据是一个接一个地顺序写入文件中的。这种方式只提供了第一个数据的存储位置，其他数据的位置则无法获得，因此要对文件内部进行修改，就必须将整个文件读到内存中进行，然后再写回文件。这种数据存取方式简单，占用磁盘空间较少，但是无法灵活而随意地存取文件数据，仅适用于不经常修改的数据的存储。顺序文件的打开与关闭、读取和写入在Visual Basic中均有相应的语句。

7.4.1.1　顺序文件的打开与关闭

要对文件进行操作，第一步就是要先打开文件。Visual　Basic提供了Open语句，使用该语句，用户可以用顺序、随机或二进制方式打开文件。Open语句的语法格式如下：

Open FileName［For Mode］［Access access］［LockType］As［＃］FileNumber［Len ＝RecordLenth］

其中：

①FileName为要操作的文件名。

②For子句中的Mode用来描述打开模式，有Output、Append、Input、Random和Binary等模式，其中Output模式打开的文件用来写入；Append模式打开的文件用来在文件尾部追回数据；Input模式打开的文件用来从文件中读取数据；Random模式打开的文件用来对文件读取或写入定长记录；Binary模式打开的文件用来读取或写入，但不要求记录定长。

③Access子句中的access用来指定文件的存取权限，包括：Read（只读）、Write（只写）或ReadWrite（可读或写）；LockType设置文件打开后其他进程对打开的文件所能进行的操作，可设置为Shared、Lock、LockRead、LockWrite和LockReadWrite等。

④FileNumber用来标识打开文件的句柄，它必须是1到511之间的整数，打开文件后就可通过FileNumber来读、写及关闭文件。

⑤在Len子句中，RecordLength用于设置以Random方式打开的文件中记录的长度（以字节为基本单位），默认的RecordLength为128。

在对顺序文件进行操作时，可用Input、Output和Append模式打开文件；在对随机文件进行操作时，可用Random模式打开文件；在对二进制类型的文件进行操作时，可用Binary模式打开文件。

在完成对文件的各种处理后，还需关闭文件以防数据丢失，这由Close语句完成。它的语法格式如下：

Close［［＃］FileNumber］

其中，FileNumber参数是Open语句打开文件时指定的句柄。当执行Close语句时，与FileNumber相对应的文件被关闭，以后可以用相同或不同的文件号重新打开此文件。

7.4.1.2　顺序文件的读写

对顺序文件可以用相应的方法进行写入操作，掌握了正确的操作方法就可以灵活使用文件。1）顺序文件的读操作

Visual Basic提供了以下过程和函数对文件进行读操作：

Input＃FileNumber，VarName［，VarName…］

Input（Length，＃FileNumber）

Line　Input＃FileNumber，VarName

其中，FileNumber表示用Open打开文件时使用的文件句柄；VarName用来存储从文件中读出数据的变量名；Input函数中的Length参数用来指明要从文件中读出字符的长度，此函数返回的是一个字符串；使用Line　Input读取数据时，会一直读到回车/换行符或文件尾为止。

2）顺序文件的写操作

对顺序文件执行写操作比较方便，Visual　Basic提供了Print＃和Write＃语句来完成写操作。

（1）Print＃语句的功能是把格式化显示的数据写入顺序文件中，其语法格式如下：

Print＃FileNumber，［OutputList］［，｜；］

其中：

①FileNumber为一有效的文件句柄。

②OutputList表示要写入文件的表达式，可用逗号将这些表达式分隔开来。

③“；”和“，”决定下一个字符输出的位置，分号表示下一个字符紧随其前面一个字符打印，逗号表示下一个字符在前面一个字符和下一个打印区开始打印，若不加“，”和“；”参数，Print＃语句会在字符结束处添加回车/换行符。

Print＃语句常和LineInput＃语句配合使用。

（2）Write＃语句的语法格式如下：

Write＃FileNumber，［OutputList］

其中：

①FileNumber为一有效的文件句柄。

②OutputList表示要写入文件的表达式，用逗号将这些表达式分隔开来。

Write＃语句常和Input＃语句配合使用。

在使用Print＃语句或Write＃语句对文件进行写操作时，文件必须以Output或Append模式打开。当以Append模式打开文件时，Print＃或Write＃语句输出的内容将追加到文件尾部。

7.4.2　计算结果的绘图

进行数值计算的过程中，通过数据的存储，会得到大量气固两相流动的信息，如何将这些枯燥的数据进行生动的展示，是我们在处理实验结果时经常遇到的问题。传统方法中，一般采取手工计算数据及用坐标绘图的方法。这种情况下，不仅耗费了大量的人力资源，而且实验结论的精度远远达不到要求，效率极低。目前，计算机已大量普及，而且高级编程语言也易于掌握。引入计算机编程进行实验数据的可视化处理，一方面可以提高实验效果，另一方面可以促使读者将所学的计算机知识应用到解决具体的物理问题中来，提高其综合能力。接下来，将分别介绍如何使用Visual　Basic软件和AutoCAD进行图像的编程绘制。

7.4.2.1　Visual　Basic绘图方法

Visual　Basic为程序设计者提供了非常丰富的绘图功能。在进行气固两相数值模拟时，可以通过调用Visual　Basic所提供的各种图形控件将模拟数据以图片的形式直观呈现。利用Visual　Basic进行编程绘图的一大优势在于程序语句简单，图形控件运用方便，绘图速度快，占用计算机资源较少，特别是针对二维模拟绘图较其他软件而言具有明显的优势。下面将介绍使用Visual　Basic绘图常用的一些基本方法和技巧。

1）坐标系统

坐标对图形绘制与文字输出的操作而言是非常重要的。坐标系统包括原点位置、坐标单位以及坐标轴的方向等方面的内容。

在窗体和图片框中绘图时，Visual　Basic提供了7种标准坐标系统供选用。此外，还可以使用自定义坐标系统。

（1）标准坐标系统

Visual　Basic的坐标系用于在二维空间定义容器对象（如窗体和图片框）中点的位置。和数学中的坐标系一样，Visual　Basic的坐标系也包含坐标原点、x坐标轴和y坐标轴。Visual Basic坐标系的默认坐标原点（0，0）在容器对象的左上角，水平方向的x坐标轴向右为正方向，垂直方向的y坐标轴向下为正方向，坐标轴的默认刻度单位是缇（Twip）。

除了缇外，Visual Basic中坐标的常用度量单位还有点（Point）、厘米和英寸等。1缇大约为1/1　440英寸，1/20点。1厘米约等于567缇，1英寸约等于1　440缇，72点等于1英寸。用户可以根据实际需要，使用ScaleMode属性改变坐标系的刻度单位。ScaleMode属性的取值如表7－1所示。

表7－1　ScaleMode属性的取值

当ScaleMode值为1～7时，是Visual　Basic已定义好的标准坐标系统，这7种标准坐标系统的原点都在对象的绘图区的左上角，水平坐标的正方向为向右，垂直坐标的正方向为向下。其中坐标系统3（ScaleMode属性的取值为3）以像素为刻度度量单位，在不同分辨率的显示器与打印机上输出结果的大小不同，是设备相关的，而其他几种标准系统都是设备无关的。坐标系统4（ScaleMode属性的取值为4）的水平与垂直度量不相同，使用时应当注意。

（2）自定义坐标系统

当窗体或图片框的ScaleMode属性为0时，使用自定义坐标系统。自定义坐标系统的原点位置和坐标单位由ScaleHeight、ScaleWidth、ScaleLeft和ScaleTop这4个属性决定。

ScaleLeft、ScaleTop属性分别指定在新坐标系统下对象绘图区左上角的水平和垂直坐标。

ScaleHeight、ScaleWidth属性决定在新坐标系统下窗体或图片框绘图区的高度与宽度。当这两个属性取负值时，会改变坐标的正方向。在自定义坐标系统下，坐标的实际单位是由对象的实际大小和ScaleHeight、ScaleWidth属性联合决定的。

例如，假设当前窗体内部显示区域的高度是2　000缇，宽度是3　000缇，此时高度和宽度的刻度单位均为1缇。

如果设置ScaleHeight＝500，则将窗体内部显示区域的高度划分为500个单位，每个单位为2 000/500，即4缇。

如果设置ScaleWidth＝1 000，则将窗体内部显示区域的高度划分为1 000个单位，每个单位为3 000/1 000，即3缇。

在使用标准坐标系统时，ScaleHeight、ScaleWidth、ScaleLeft和ScaleTop这4个属性也是可用的，它们分别反映出在当前标准坐标系统下相应的值，ScaleLeft、ScaleTop的值都为0，ScaleHeight、ScaleWidth的值为以当前坐标单位为度量的标准绘图区的高度与宽度。如果在标准坐标系统下，改变了这4个属性中任意一个的值，都会自动使用自定义坐标系统，ScaleMode属性被自动设置为0。

也可以使用Scale方法设置一个自定义坐标系统，其格式如下：

［object.］Scale（x1，y1）－（x2，y2）

其中：

①object为窗体或图片框对象名。

②x1，y1为对象的绘图区左上角在新的自定义坐标系统下的坐标。③x2，y2为对象的绘图区右下角在新的自定义坐标系统下的坐标。

④对Scale方法的调用等价于对前面提到的4个属性的设置，关系如下：

ScaleLeft＝x1 ScaleTop＝y1

ScaleWidth＝x2－x1 ScaleHeight＝y2－y1

（3）当前坐标

当在容器中绘制图形或输出结果时，经常要将它们定位在某一希望的位置，这就必须获得某一点的坐标，即当前坐标。Visual　Basic使用CurrentX和CurrentY属性设置或返回当前坐标的水平坐标和垂直坐标。

2）颜色

计算机领域中一般采用RGB颜色模型，认为任何颜色都是由红（R）、绿（G）、蓝（B）3种颜色按不同比例混合的结果。因此要设定一种颜色，只要指定其红、绿、蓝分量的大小即可。Visual Basic中颜色的表示就是基于这个概念。要得到一种颜色有以下几种方法：

（1）使用RGB函数

可以使用Visual　Basic的内部函数RGB返回一个颜色值，此函数有3个参数，取值范围都是0～255，分别表示所要颜色中红（R）、绿（G）、蓝（B）分量的大小，如：RGB（0，0，0）返回黑色，RGB（255，0，0）返回红色，RGB（0，0，255）返回蓝色。

（2）使用长整型数

其实，RGB函数返回的只是一个长整型数。在Visual Basic中颜色就是由长整型数表示的，所以可以直接用长整型数来指定一个颜色。

在Visual Basic中，表示一个颜色的长整型数的4个字节中，从高位到低位，第1个字节的所有位都为0，第2个字节表示的是蓝色（B）分量的大小，第3个字节表示的是绿色（G）分量的大小，第4个字节表示的是红色（R）分量的大小。每个分量值的十六进制形式都是＆H00～＆HFF，十进制为0～255。

用十六进制的长整型常量表示一个颜色值是很直观的，每个颜色分量占两个十六进制位，其表示格式为：

＆H00BBGGRR

例如，下面是一些表示颜色的长整型数：

＆H00000000（黑色）　＆H00FFFFFF（白色）　＆H00FF0000（浅蓝）

＆H00800000（深蓝）　＆H0000FFFF（浅黄）　＆H00008080（深黄）

在源程序中输入长整型数时，编辑器会自动删掉前面不必要的0。

（3）使用系统颜色

如果一个表示颜色的长整型数的最高位为1，即它的第一个字节的值为＆H80时，则不表示一个具体的RGB颜色值，而是一个系统颜色。系统颜色是由用户在Windows控制面板的“显示”属性中设定的各界面元素（如菜单、滚动条、桌面等）的颜色，同一个系统颜色在不同计算机上的具体设置可能不同。系统颜色有25个（＆H80000000～＆H80000018），它们的具体意义如表7－2所示。

表7－2　系统颜色常量

续表7－2

（4）使用内部颜色常量

Visual　Basic为一些常用颜色定义了内部常量，颜色常量的特点是直观、易于记忆。Visual Basic中的常用内部颜色常量如表7－3所示。

表7－3　Visual Basic中的常用内部颜色常量

（5）使用QBColor函数

Visual　Basic保留了Quick　Basic的QBColor函数。该函数用一个整数值对应RGB的常用颜色值，其格式如下：

QBColor（颜色值）

其中，“颜色值”的取值范围为0～15，共可表示16种颜色。函数根据参数“颜色值”返回一个表示颜色的长整型数。不同的参数值与返回颜色之间的对应关系如表7－4表示。

表7－4　QBColor函数的参数与返回颜色

3）画点方法

画点方法（PSet）可以在窗体或图片框的指定位置上使用指定颜色画一个点。PSet方法的语法如下：

［object.］PSet［Step］（x，y）［，color］

其中：

①Object为窗体或图片框的对象名。

②［Step］（x，y）指定画点位置的坐标，如没有指定Step关键字，则（x，y）指的是绝对坐标（相对于窗体或图片框绘图区的左上角）；如果指定Step关键字，则（x，y）表示的是相对于（CurrentX，CurrentY）点的相对坐标。注意，把坐标参数（x，y）括起来的小括号是不可少的。

③参数color用来指定点的颜色，它可以是长整型数、常量或颜色函数。如果没有指定color，PSet将点的颜色设置为前景色（ForeColor）。

PSet方法执行完后，对象的CurrentX、CurrentY属性值会被自动设置为画点位置的绝对坐标。

4）画直线、矩形方法

Line方法可以在窗体或图片框上绘制一条直线段或一个矩形，其语法为：

［object.］Line［［Step］（x1，y1）］－［Step］（x2，y2）［，color］［，B［F］］

其中：

①object为窗体或图片框对象名。

②参数［Step］（x1，y1）指定起始坐标，［Step］（x2，y2）指定终止坐标。如果有参数B，则绘制以给定两点为对角的矩形，否则画出以给定两点为端点的直线段。

③参数color指定直线或矩形边框的颜色。如果有参数F，则用边框颜色填充矩形。无参数B时，不能使用参数F。如果（x2，y2）参数前有Step关键字，表示是以起始点绝对坐标为基准的相对坐标。

执行完此方法后，对象的CurrentX、CurrentY属性值即为终点的坐标。

如果在调用Line方法时，省略了参数“［Step］（x1，y1）”，则会把CurrentX、CurrentY属性的值作为起始点的坐标，相当于“［Step］（0，0）”。

另外，调用一次带参数B的Line方法只能画出水平或垂直的矩形。如果要绘制任意方向的矩形，可以调用4次Line方法画出矩形的4条边。

5）画圆方法

Circle方法可以在窗体或图片框上绘制圆形、椭圆或弧，其语法为：

［object.］Circle［Step］（x，y），radius［，color］［，start］［，end］［，aspect］

其中：

①object为窗体或图片框对象名。

②参数［Step］（x，y）指定圆心或椭圆中心的坐标，radius指定圆的半径或椭圆的长半轴，color为线条颜色。

③start与end指定弧的起止角度（单位是弧度），如果被省略，则绘制出完整的圆或椭圆。

④aspect指定圆度（垂直半轴与水平半轴长度之比），当它为1或省略时，绘出的是一个圆，取其他值时为椭圆。

当Circle方法的start或end参数为负值时，绘制的是与相应的正值相向的一段弧，只不过多画出从端点到中心的连线。

此方法执行后，对象的CurrentX、CurrentY属性的值会等于圆心或椭圆中心的坐标。

6）清除图形方法

Cls方法用来清除窗体或图片框上由Print、PSet、Line、Circle等方法输出的文字、图形和图像。清除之后，CurrentX和CurrentY属性值都被设为0。其格式为：

［object.］Cls

其中，object是窗体或图片框的对象名。Cls方法没有参数。

Cls方法不会清除窗体和图片框上由Picture属性设置的背景图像，更不会清除窗体或图片框上的控件对象。

7）线框和线形属性

（1）DrawWidth属性设置绘图方法绘制的图形的线条样式，其取值范围为1～32　767，以像素为单位，默认值为1，即1个像素宽。

如果DrawWidth属性值大于1，画出的图形是实线；如果DrawWidth属性值等于1，可以画出由DrawStyle定义的各种线型。

（2）DrawStyle属性设置绘图方法绘制的图形的线条宽度。此属性的取值范围为0～6，具体意义如表7－5所示。

表7－5　DrawStyle属性值

8）填充颜色属性和填充样式属性

（1）FillColor属性设置由Circle和Line方法生成的圆、矩形等封闭图形的内部填充颜色。

（2）FillStyle属性设置Shape控件所画图形的填充样式，也可以设置由Circle和Line图形方法生成的封闭图形的填充样式。此属性的取值范围为0～7，具体意义如表7－6所示。

（3）FillStyle属性的默认值为1（透明），此时，FillColor属性的值被忽略。

表7－6　FillStyle属性值

9）自动重画属性

应用程序在运行时其窗体经常被移动或被其他窗体覆盖，要想保持窗体中的内容（图形等）不丢失，就要在窗体移动、改变大小或覆盖它的窗体移开后重新显示（绘制）窗体中的内容。一般来说，Windows管理或控制窗口、控件的重新显示，而窗体和图片框内图形的重新显示必须由用户的应用程序来控制。AutoReDraw属性就提供了重新显示窗体和图片框内图形的功能。

当AutoReDraw属性设置为False（默认值）时，对象中的图形不具有持久性，即当窗体或图片框全部或部分被其他窗体遮盖后再重新显示时，绘图方法产生的图形不会被自动重画，对象上的图形将丢失。

当AutoReDraw属性设置为True时，表示对象的自动重画功能有效，使用绘图方法绘制的图形会被保存在内存中，当窗体或图片框的全部或部分被其他窗体遮盖后又显示出来时，图形会自动重画。

7.4.2.2　AutoLISP绘图方法

当采用Visual Basic进行三维绘图时，其绘图程序的编写较之二维情况变得复杂起来，其中牵涉到视角转换、图像投影等问题，而且绘制的图像质量不高，立体效果较差。为了制作高品质的图像文件，可以采用嵌入在AutoCAD内部的编程语言——AutoLISP。

AutoLISP是由Autodesk公司开发的一种LISP程序语言，LISP（List Processor）是人工智能领域中广泛采用的一种程序设计语言，主要用于人工智能、机器人、专家系统、博弈和定理证明等领域。LISP也被称为符号式语言，因为它处理的对象是符号表达式。LISP语言的程序和数据都以符号表达式的形式表示，即一个LISP程序可以把另一个LISP程序作为它的数据来处理。

AutoLISP采用了和LISP最相近的语法和习惯约定，具有Common　LISP的特性，但又针对AutoCAD增加了许多功能。例如，可以把AutoLISP程序和AutoCAD的绘图命令透明地结合起来，使设计和绘图完全融为一体。还可以实现对AutoCAD当前图形数据库的直接访问、修改，为实现对屏幕图形的实时修改、交互设计、参数化设计及绘图领域中应用人工智能提供了方便。概括地说，AutoLISP综合了人工智能语言LISP的特性和AutoCAD强大的图形编辑功能的特点，可谓是一种人工智能绘图语言。通过AutoLISP编程，可以为工程师节省很多时间。AutoLISP语言作为嵌入在AutoCAD内部的具有智能特点的编程语言，是开发应用AutoCAD不可缺少的工具。

学习AutoLISP是非常容易的，对初学者而言，即使没有学习过任何的程序语言，都能很快上手，写出精彩漂亮的AutoLISP程序。

1）AutoLISP的特点

（1）语法简单：不用特殊的变量定义，非常富有弹性，比起其他的程序语言，它的语法可说是非常简单而又有其独特的风格。

（2）功能函数强大：除一般性的功能函数外，还拥有为数不少的控制配合AutoCAD的特殊函数，再加上AutoLISP可直接调用执行所有AutoCAD的命令以及掌握运用所有的AutoCAD系统变量，功能之强大令人欣喜不已。

（3）对撰写环境不挑剔：只要是一般的窗口文本编辑软件都适用，如记事本、写字板、UltraEdit等。

（4）直译式程序：不用再编译，“即写即测、即测即用”，马上可以在AutoCAD中响应，查看效果。

（5）横跨各操作平台：只要是AutoCAD配合的操作系统，如Windows　XP、Wondows　7等，都可以加载与执行。

2）AutoLISP表达式语法规则

（1）规则1：以括号组成表达式，左右括号“（”与“）”一定要成双成对、相对称，内部的字符串双引号“"”也要成双成对。

（2）规则2：表达式符合以下格式：

（函数名　操作数　操作数　操作数）

①操作函数包括功能函数与自定义函数。

②操作数（自变量）包括：

·整数（Integer），如8，－17，500，999；

·实数（Real），如8.5，－17.456；

·字符串（String），如"AutoCAD"，"123"；

·列表（List），如（"a""b""c"），（x，y）；

·对象名称代码，如＜对象名称：6340510＞；

·文件代码，如＜文件：＃6562ea0＞；

·选择集代码，如＜选择集：3＞。

（3）规则3：表达式中的操作数，可以是标准AutoLISP函数或另一表达式或子程序。

（4）规则4：多重的括号表达式中，运算的先后顺序是“由内而外、由左而右”。

（5）规则5：以文件格式存在的AutoLISP程序（ASCII文件），其扩展名最好是“.lsp”。

（6）规则6：对于编写的环境，只要是一般的文件编辑软件，可编辑ASCII文件的都适用。

（7）规则7：使用Defun功能函数定义新的命令或新的功能函数。

（8）规则8：新定义的功能函数名称若为“C：函数名”，则此函数可以作为AutoCAD新命令。

（9）规则9：加载AutoLISP程序的做法：

①命令行直接输入（Load“LISP主文件名”）。

②使用Appload命令加载程序。

③将LISP置于menu中，自动加载与执行。

（10）规则10：AutoLISP程序中，在分号后的内容均为批注，程序不处理。适时地增加批注，将使程序更具可读性、学习性及完整性。

（11）规则11：AutoLISP最常用的变量类型是“整数”、“实数”、“字符串”、“列表”4种，变量的类型依据设定值而自动定义，变量会一直存储该值，直到被重新定值或绘图结束后自动消失。

（12）规则12：使用Setq功能函数为变量赋值（Setq　变量名称　设定值）。

（13）规则13：欲在AutoCAD的环境中查看一变量值，在命令行输入“！变量名”即可。

（14）规则14：在（Defun　C：函数名（自变量/变量）...）程序代码中，程序中的变量若在“/”右边，则称为局部变量，否则为全局变量。

与Visual　Basic类似，在使用AutoLISP进行编程绘图时，同样要牵涉坐标系统、颜色以及二维或三维图形绘制的程序命令，由于篇幅有限，这里不再赘述，感兴趣的读者可阅读相关资料。通过AutoLISP调用所存储的数据信息在AutoCAD中连续绘图，也可以对所绘制图形进行渲染和光照处理，以达到完美效果，如图7－65所示。

图7－65　LISP语言绘制图效果

7.4.3　动画制作

通过Visual　Basic和AutoCAD等软件可以调用不同时刻的计算数据，从而可以按时间顺序绘制出一系列的图像，若将这些静态图像连续地显示出来便可形成动画，能够生动再现整个计算过程。动画可以重复播放，便于我们仔细观察气固两相流动的变化过程，从而深刻了解系统的内部机理。

目前，能够将图像制作成动画的软件种类繁多，而GIF　Movie　Gear便是其中一款小巧实

用的软件。GIF　Movie　Gear是能够实现GIF文件的制作、编辑、优化、转换的软件，可以用它打开BMP/GIF/JPG/PNG/PSD/AVI/CUR/ICO等格式的文件并将它们转换或混合为GIF格式的文件，并保存为BMP/GIF/JPG/PNG/PSD/AVI/CUR/ICO甚至SWF格式的文件。还可以用它剪切、缩放、旋转导入的图像文件，调整帧的顺序和延迟时间，更改循环次数，并用多种方法对其进行优化以减小文件体积。此外，GIF　Movie　Gear还能调用任意应用程序对帧进行实时编辑，为GIF文件添加注释以及输出HTML代码，方便在网页中调用图像。

GIF　Movie　Gear几乎拥有制作GIF动画所需要的全部编辑功能，无需再用其他的图型软件辅助。它可以处理背景透明化而且做法容易，做好的图片可以做最佳化处理使图片减肥。另外，它除了可以把做好的图片存成GIF的动画图外，还可支持AVI、PSD、JPEG、BMP、GIF等格式的输出。

动画实际上是连续的静态画面，因此在制作动画之前，我们要首先准备好动画播放过程中的一系列单帧图像。可以先利用其他平面绘图软件制作好单帧图像之后再利用GIF Movie　Gear来将其制作成GIF动画。打开GIF　Movie　Gear之后我们看到的主界面上有“打开文件”以及“插入帧”按钮，如图7－66所示。点击“打开文件”按钮，弹出文件选择对话框，我们可以一次选择多个图像文件合并或者制作成动画。

导入制作动画所需图像后会形成动画预览，如图7－67所示。点击对话框右侧的 按钮，出现了新增加的界面（如图7－68所示），这时，我们可以在“所有帧延迟”设置区右侧文本框中填写1～10的整数，再点击旁边的绿色箭头 来确定并调节动画播放的速度，所填写的数字越大，播放的速度越慢，反之则越快。图7－69为循环流化床中颗粒流动的动画演示结果。

图7－66　GIF　Movie　Gear开始界面

图7－67　动画预览

图7－68　设置动画播放速度

图7－69　动画演示结果

动画制作完成后，依次点击“文件”→“另存为（A）...”，我们可以将其保存为AVI、GIF、SWF等多种格式的文件（如图7－70、7－71所示）。

图7－70　动画的保存

图7－71　动画文件的保存格式