单喷口流化的数值模拟

第8章　气固两相流动数值模拟的应用

在前7章内容的基础上，为加深对气固两相流动数值模拟相关知识的理解，本章选取了9个典型案例来介绍数值模拟方法的应用。这些案例都是近些年来科学研究以及工程实际中所遇到的问题，每个案例都具有各自不同的特征，以供读者参考。

8.1　料仓中颗粒卸料过程的流动特性

1）数值模拟研究背景

料仓是工业生产中颗粒物储存的常用设备，除了可以用作储存容器外，还可以作为喂料器、混合器等。根据储存量的需要，料仓的容量变化较大，而且在形状方面也各有不同，如楔形料仓和圆锥形料仓。除此之外，料仓中的储料也是多种多样的，包括不同尺寸、不同形态、不同粘性等方面。

图8－1　料仓卸料时两种主要的流型示意图

根据料仓的几何形状、物料的种类和特性的不同，料仓的卸料主要有两种类型：中心流与整体流，如图8－1所示。整体流是指卸料时所有散体都处于运动状态，并贴着垂直部分的仓壁和收缩的料斗壁滑移，散料的流动通道与料仓壁是一致的；中心流是指卸料时散体沿着卸料口上端的管状通道往下流动的流动形式，即随着管内散体的流出，散体上表面在下降，上部散体不断通过管状通道流向仓外，可能形成先进而后出的流动效应。料仓在工业生产中可能出现的流动问题中，如架桥、鼠洞、喷流、离析等都与中心流有关。因此，使料仓卸料尽可能呈现整体流，则上述大多数问题都可以避免，例如可采取增加料仓的卸料口尺寸、敷设较为光滑的衬体材料、安装震动装置、加松动风以及安装改流体等措施。其中，在料仓中的某个适当位置安装一定形状改流体的方法通常更为方便，可有效地改变料仓中物料流动状态，使之成为整体流。

然而，如何确定改流体的位置和改流体的形状存在多种不同的选择，给工程设计带来一定的困难。如果采用实验研究的方法，需要对不同改流体的尺寸和安装位置进行反复试验和比较才能确定，需要耗费大量的人力物力。如果完全根据经验来确定则存在一定的风险，并难以达到最优结构和效果，这在很大程度上限制了改流体的广泛应用。针对上述情况，采用数值模拟可较好地克服这些问题。通过编程，在计算机上可对不同改流体的形状和安装位置进行比较和分析，了解颗粒在料仓中的流动特性，通过比较和筛选获得最佳选择方案，从而作为实验方案的依据，可以大大减少实验的数量并提高实验的质量，成为寻求和确定工程方案的有效手段。

下面将通过一个例子来介绍分别在无改流体以及安装改流体的情况下，料仓中颗粒的卸料流动特性。

2）所模拟的物理模型

所模拟料仓的基本结构如图8－2所示，料仓的高度为H，宽度为W，半顶角为θ，底部出口的宽度为W0，改流体的截面为一等腰三角形，其尖顶安放于料仓Hi高度的位置，改流体的半顶角为θi，长度为Li。

3）所采用的模拟方法和主要数学模型

料仓内的流动为散体颗粒的流动，由于料仓中空气处于静止状态，因此不考虑空气对颗粒的曳力作用。根据目前计算机硬件条件和数值模拟的发展水平，采用拉格朗日方法对离散颗粒的受力和运动进行描述，采用软球模型进行建模，该模型适用于稠密气固两相流动乃至颗粒发生堆积情况下的数值模拟，具体数学模型可参见本书第6章的内容。

4）数值模拟结果与分析

图8－3为无改流体情况下颗粒物料在料仓卸料过程的数值模拟结果，为了更清楚地观察和分析料仓中不同区域颗粒的流动特性，在仓体的不同高度分别放置其他颜色的颗粒层，读者可以在数值模拟过程中对每一颗粒通过设置一个记忆颗粒颜色的变量来记录颗粒的初始颜色。在初始阶段，颗粒在重力作用下向下流动，料仓表层的形状基本保持不变；随着颗粒的下落，中心区域物料与壁面区域物料的速度差逐渐增大，表层颗粒开始向中心汇聚，颗粒的流动逐渐变为中心流。

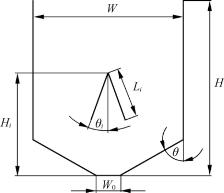
图8－2　料仓和改流体的几何形状

图8－3　无改流体时料仓卸料过程的模拟结果

由图8－4所示的数值模拟结果可见，在无改流体情况下，料仓的卸料过程为中心流流型。在出口处，由于颗粒接触碰撞的机会较少，可以自由下落，速度较大，称之为自由下落区，其上部为颗粒垂直流动区。靠近壁面处，颗粒速度很小甚至为零，称之为半停滞区。在半停滞区上部为颗粒擦过半停滞区向出口中心方向流动的慢速流动区。而在物料自由表面处，颗粒向着中心处快速滑动，称之为快速流动区。图8－4所示的模拟结果与Brown与Hawksley提出的颗粒在料仓中的流动区域划分是一致的。

图8－5是安装改流体后颗粒的流动状态。由图中可以看出，在改流体上方，颗粒一直保持整体流的流动形

式，颗粒表层物料均匀下降，示踪层呈水平分布，见图8－5（a）。在通过改流体时，中心处的颗粒速度由于改流体壁面的影响，比两侧垂直流动区的速度小，当颗粒流动到渐缩下料段，由于倾斜壁面的影响和出口处自由下落区的存在，使得中心处颗粒流速稍快，边壁处稍慢。

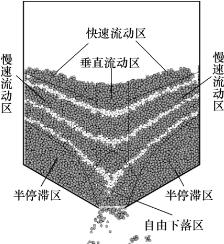
图8－4　无改流体时流动区域示意图

图8－5　安置改流体后料仓中颗粒流动的模拟结果

由此可见，与无改流体相比，改流体的安装在料仓上部形成了两个狭槽开口，颗粒沿着改流体壁面流动，垂直流动区明显增加，料仓内垂直中心轴线附近颗粒的快速流动得到了控制，且两侧壁附近颗粒在很短时间内由静止态转为移动态，半停滞区得到显著改善。这表明，料仓中加设改流体可以有效地实现仓内物料流动由中心流向整体流转换。

图8－6和图8－7是采用软球模型所模拟的另外两组颗粒从漏斗中下落的过程。图8－6所模拟的条件是颗粒粒径相同，但密度不同，深色颗粒的密度大于浅色颗粒的密度，两种颗粒在漏斗中随机分布。通过漏斗后可以发现，密度大的颗粒倾向于先从漏斗中漏完，漏斗中最后漏完的颗粒均为浅色的密度较小的颗粒。

图8－6　颗粒粒径一样而密度不同的情况下颗粒从漏斗中下落的过程

图8－7所模拟的条件是颗粒密度相同，但粒径不同，深色颗粒的粒径大于浅色颗粒的粒径，两种颗粒在漏斗中随机分布。通过漏斗后可以发现，粒径小的颗粒倾向于先从漏斗中漏完，漏斗中最后漏完的颗粒均为深色的粒径较大的颗粒。

图8－7　颗粒密度一样而粒径不同的情况下颗粒从漏斗中下落的过程

上述两种漏斗流的数值模拟结果与实验所反映的规律相同。

8.2　球磨机内不同粒径颗粒的运动特性

1）数值模拟研究背景

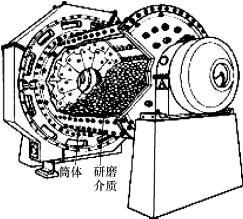
图8－8　球磨机外形简图

球磨机是一种物料破碎和研磨装置，因其具有结构简单、性能稳定、易于维护等优点，而被广泛应用于火力发电、水泥生产、冶金、陶瓷和耐火材料制备等领域。如图8－8所示，球磨机由水平筒体、进出料空心轴及磨头等部分组成，筒体为圆筒结构，筒内装有研磨体，一般为钢制圆球，按不同直径和一定比例装入筒中。

需要研磨的物料由球磨机进料端空心轴装入筒体内，当球磨机筒体转动时，钢球由于衬板和摩擦力的作用被带到一定高度后在自身的重力作用下抛落，下落的钢球与物料产生撞击和摩擦而将物料研磨成粉末，当完成研磨作业后，粉状物料通过卸料板排出。

以往对球磨机工作性能的探讨多采用理论与实验或者从工程实践中摸索总结的研究方法。理论分析建立在一定的假设和简化基础之上，难以保证与复杂的实际情况相吻合；实验中由于受到设备和测试的限制，难以得到不同粒径钢球在球磨机中运行特性的准确数据，使得深层次的研究有很大难度。针对以上问题，采用计算机数值模拟的方法可清晰地获得不同转速、不同钢球填充量、不同衬板结构条件下，不同粒径钢球的运行规律，通过统计钢球间的撞击次数可获得球磨机的研磨能力，从而为研究球磨机转速、钢球填充率、球径的合理组合、球料比、衬板形式和个数等因素对球磨机工作性能的影响，提高球磨机的磨矿效率提供了新的研究手段和工具。

2）所模拟的物理模型

所模拟球磨机的筒体结构如图8－9所示，在圆周方向均匀分布了6个圆柱形衬板。球磨机内放置了两种不同粒径的钢球，拟希望通过数值模拟结果来观察不同粒径钢球在球磨机中的运动特性和差异。

3）所采用的模拟方法和主要数学模型

球磨机筒体按给定的转速边界条件匀速转动，筒内的钢球在衬板和筒壁摩擦力的作用下产生运动，由于球磨机中空气的流速很小，因此气相的作用可以忽略不计。建模采用拉格朗日方法，通过软球模型对颗粒间的作用进行描述，因为对于球磨机内钢球直径相对较大、钢球相互堆积的运动情形，应用软球模型尤为适合。具体数学模型可参见本书第6章的内容。

4）数值模拟结果与分析

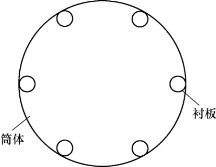
图8－9　球磨机筒体结构简图

图8－10　球磨机中颗粒的混合过程

图8－10为球磨机中钢球运动过程的数值模拟结果，根据不同的球径，在绘图时采用不同的颜色，以便观察不同直径钢球的运动情况。从数值模拟结果可见，随着球磨机按顺时针方向转动，在衬板和筒壁摩擦力的作用下，钢球被球磨机筒体带到一定高度后滑下，较小直径的球体倾向于沉积在堆积球体的底部，而较大直径的钢球倾向于堆积在较小球体的上方。通过该数值模拟平台，可以清楚地观察和研究钢球运动特性随球磨机转速变化的情况。

8.3　循环流化床内气固两相流动特性

1）数值模拟研究背景

循环流化床装置常用于能源、环保、化工、物料加工等领域。循环流化床内物料颗粒从床的底部进入床内，从床的顶部流出。物料粒径、物料密度、气流风速等运行条件发生改变，床内物料流化特征也随之改变，如物料在流化过程中倾向于汇聚、贴壁物料会在壁面附近发生堆积乃至发生沉降等均为循环流化床内的流动特征。研究人员通常关心不同粒度或密度的混合物料在床内的流动特性、停留时间、径向分布特征等信息，采用计算机数值模拟，无疑是探讨上述信息的有效工具。

2）所模拟的物理模型

相同粒径、相同密度的床料从循环流化床底部均匀进入，在气流的作用下流向床顶并从顶部流出，拟建立数值模拟研究平台，通过数值模拟的方法分析和研究物料在床内的运动特性。

3）所采用的模拟方法和主要数学模型

对于循环流化床内气固两相流动的数值模拟，可将颗粒相视为连续流体，采用双流体模型进行模拟。近些年来，随着计算机计算能力的快速提高，为了能够更加准确地分析不同性质颗粒在床内的分布特征，通常将气、固两相分开处理，分别用欧拉方法模拟气相，用拉格朗日方法模拟离散颗粒相，以充分发挥这两种方法的长处。在采用单向耦合的情况下，在每一时间步长内仅需考虑气相对颗粒的曳力作用；在采用双向耦合的情况下，在经过若干计算时间步长后，由于不同计算网格内颗粒相容积份额的变化，需要对气相场重新进行计算，以提高数值模拟结果的准确性。

下面给出的例子采用将气相和离散颗粒相分开处理的方法，在以拉格朗日方法模拟离散颗粒运动时，采用硬球模型描述颗粒间的相互作用，气相场数学模型的主体为用欧拉方法建立的N－S方程，采用单向耦合的方法处理气固两相间的作用。

4）数值模拟结果与分析

图8－11给出的是数值模拟结果，从图中可以清楚地观察到循环流化床内的颗粒运动随时间的变化过程，其中一个十分有趣的现象是虽然颗粒在进入床体时被设置为均匀分布，但随着颗粒在床内的向上运动，颗粒的汇聚现象逐渐显现，即颗粒的空间分布不再均匀。此外，从颗粒运动的动画过程，还可清楚地观察到床壁面附近区域颗粒产生回流的现象。

基于以上所构建的数值模拟平台，通过改变表观风速、颗粒特性以及同固相流量，可进行气固两相流动深层次的机理发掘和内在规律的研究。

图8－11　循环流化床内气固两相流动过程

8.4　单喷口流化的数值模拟

1）数值模拟研究背景

流化床布风板上开有很多气孔，也有采用风帽结构的布风板，不同形式的布风板对床内物料的流化状态会产生影响，例如，将布风板上的气孔由直孔改为沿周向倾斜的斜孔，则气流使床内物料产生流化的同时还促使物料在床内发生转动。本案例模拟的是在一个竖直气孔的作用下床内颗粒的流化特征。

2）所模拟的物理模型

在气流分布板上方，取单个气孔所对应的三维床体，如图8－12所示。为了便于观察在流化过程中床内颗粒的混合情况，流化前投入床内的物料分为三层，分别取三种不同颜色，颗粒大小和密度相同，通过数值模拟观察气流进入床层后的颗粒流化与混合状况。值得说明的是，该种单孔流化所得到的结果与实际多孔气流分布板的流化结果有很大不同，因为在多孔情况下，孔与孔之间的气流会发生合并而形成大的气泡。

图8－12　单孔气流流化

3）主要数学模型

由于所模拟的床料颗粒数目不是很多，在建模时可将气相和离散颗粒相分开处理，对气相场的建模采用欧拉方法，而对离散颗粒相的运动则采用拉格朗日方法，用软球模型加以描述。根据目前计算机硬件条件，若采用软球模型，在颗粒量不超过10　000个的情况下，采用普通工作站进行模拟计算是可行的。

描述喷动床内三维气相流场的数学模型包括连续性方程、动量守恒方程，另外，在湍流情况下，还需附加k－ε双方程湍流模型。

计算固相运动时，采用拉格朗日方法跟踪每一个颗粒的运动，采用软球模型描述离散颗粒间的相互作用。床内颗粒的初始位置的确定，是在未加入气流作用前，由床上部按照颗粒自由落体运动投入床内，即在投入颗粒时就开始跟踪进入计算区域的颗粒，颗粒进入床层后，通过不断碰撞，最后达到静止，成为流化前的初始堆积状态［图8－13（a）］。具体数学模型可参见本书第5、6章的内容。

图8－13　单喷口流化的数值模拟结果

4）数值模拟结果与分析

图8－13为单喷口流化床中颗粒在气流进入床层后的演变过程。从数值模拟结果可见，在气流进入床层前，三种不同颜色的颗粒依次在不同高度堆放于床体下部，气体经由喷嘴垂直向上射入床体底部中心的入口，形成一个随流体流速的增大而逐渐向上延伸的射流区。当该区域颗粒上升到一定高度时，颗粒因自身重力而向床体左右壁面方向回落，回落的颗粒沿壁面附近向下运动并回落至床层下部，然后又渗入中心射流区被重新夹带上来，从而形成极有规律的颗粒内循环运动。设想若单喷口流化床用于干燥物料，则这种循环运动不仅使得气流夹带颗粒，促进气流与颗粒间的热质交换，达到加速干燥的目的，而且喷射区周围颗粒的相互渗透也促进了颗粒自身间的碰撞混合，可有效地避免局部干燥不均匀的现象，在干燥过程中有助于使产品湿含量保持一致。同时，通过床层颗粒的内部循环，构成颗粒与流体在床层内有规律的间歇接触。

8.5　洗涤冷却室内含渣气体穿越液池的气泡特性及气固分离过程

1）数值模拟研究背景

图8－14　水煤浆气化炉示意图

在洁净煤技术体系中，煤气化是其中的重要技术之一，而德士古气化炉又是一种常见的煤气化方式。水煤浆在气化炉燃烧室内产生的高温合成气通过冷却环和下降管进入激冷室，需要在激冷室内达到快速冷却。目前采用的冷却方式是让高温合成气通过下降管进入液池，在穿越液池过程中合成气与水接触而得到快速冷却，同时合成气中煤的熔渣与合成气发生分离，从而使得高温合成气得到冷却和洗涤（图8－14）。气体的冷却强度与合成气在穿越液池的过程中所形成的气泡大小密切相关，在相同气体流量的情况下，小尺寸的气泡具有气液两相间较大的接触面积，从而可以达到较好的冷却效果。气泡尺寸应与液池深度、气体流速、下降管直径等因素有关，为探讨这些因素的影响，了解洗涤冷却室内气、液、固三相的运动规律，因而开展以下数值模拟研究。

2）所模拟的物理模型

为了便于计算，建模前将洗涤冷却室做适当的简化，所模拟的水煤浆气化炉洗涤冷却室的结构如图8－15所示，图中箭头为气体流动方向，来自燃烧室的高温合成气由中心下降管向下流入液池，穿越液池的过程中形成气泡，而后由液池上方流出洗涤冷却室。合成气在穿越液池的过程中，气体中所携带的固态煤渣在液池中与气体产生分离并沉降到液池底部。

3）所采用的模拟方法和主要数学模型

所模拟的物理模型包括气、液、固三相流动，根据该三相的形态特征，建模时将气、液两相视为连续相，采用欧拉方法建立气液连续相流动控制方程。气、液两相共用一套连续性方程和纳维－斯托克斯方程，出现在方程中的密度、粘度等属性由存在于每一控制容积中的分相决定。湍流模型采用基于重整化群（renormalization group）理论的RNGk－ε湍流方程，气、液两相间界面的跟踪采用VOF模型。

离散颗粒相运动的建模采用拉格朗日方法，在气、液两相构成的流体系统中，每个颗粒都受到周围流体的作用，此外，颗粒与邻近颗粒也可能发生相互碰撞作用。在跟踪离散颗粒运动的过程中，需要判断每个颗粒当前所在位置周围流体的性质，即是液体还是气体，根据流体属性计算相应的流体曳力，采用软球模型描述颗粒间可能发生的相互接触与碰撞，然后根据所有力的合力计算颗粒在当前时间步长内的运动。

在颗粒量较大的情况下，软球模型会遇到计算时间过长的问题，因此对于颗粒间的相互作用，也可采用硬球模型进行计算，并可结合蒙特卡洛方法，将一个模拟计算颗粒视为多个物理颗粒的代表，从而使得模拟的颗粒数远小于实际的颗粒数，提高计算效率。

4）数值模拟结果与分析

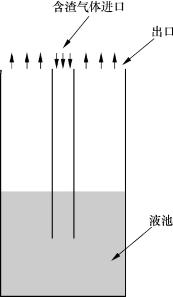
图8－15　洗涤冷却
室结构示意图

图8－16　不同时刻含渣气体穿越液池气、液、固三相流动分离行为

图8－16为数值模拟计算得到的气、液、固三相流动与分离过程。从数值模拟结果可见，气体携带着不同粒径的固体颗粒进入液池，在穿越液池的过程中，气流在液池中生成气泡，气泡运动到液池表面附近发生破碎，形成液体的飞溅。气流中的颗粒随气体进入液池，较大粒径的颗粒沉降到液池底部，相对较小粒径的颗粒则被气体带到了液池的鼓泡区，在泡沫作用阶段，颗粒被液体捕获并在液池中悬浮，随液体一起流动并逐渐沉降。一些粒径非常细小的颗粒则可能被下降管外壁上升的气流所夹带而钻出液面。在液池上部空间，随气流一起钻出液面的大部分细小颗粒往往又被下落的液滴所捕获，一同落回液池中。从图中还可以看到，在经过冲击作用阶段、泡沫作用阶段以及淋浴作用阶段的三重洗涤净化作用之后，只有较少的细小颗粒会进入液池上部的空间，并随气体一道流出洗涤冷却室。图8－17展示了数值模拟计算得到的某一时刻不同粒径颗粒在随气体穿越液池的过程中所经历的流动分离过程，可以更加清晰地了解到颗粒的运动、分离的整个过程。

图8－17　离散颗粒运动、分离过程的数值模拟结果及分析

8.6　细长杆状颗粒流化特性研究

1）数值模拟研究背景

目前在气固两相流动的计算机数值模拟研究中，对球形颗粒运动特性的研究较多，而在处理非球形颗粒时则存在较大难处，通常是采用人为定义的等效直径及颗粒的形状系数、比表面积等描述非球形颗粒的尺寸和外部形状的变化，将其简化成球形颗粒进行计算，然后通过非球形颗粒的相关系数对结果进行修正，以减少研究的复杂性。这对于近球形颗粒的情况可以认为是合理的，但对于一些偏离球形较远的固相颗粒的情况，如长径比较大的细长杆状颗粒，将它们进行球形化处理势必会导致较大的误差，使研究结果失去指导实际的意义。

细长杆状颗粒是一类极具代表性的异形颗粒：颗粒细长，形状在轴向上占优，非各向同性，它们的受力、转动和取向分布复杂，这些都增加了研究的难度。目前对于此类复杂异形颗粒的研究相对较少，而细长杆状颗粒作为循环流化床物料在工业实际中却有应用，如燃烧棉花秸秆的循环流化床锅炉、纤维的气力输送等。因此，研究细长杆状颗粒的流化特性具有重要意义。

2）所模拟的物理模型

针对循环流化床内细长粒子进行数值模拟，床体结构为图8－18所示的提升管段，细长粒子由提升管底部进入床层，在气流的作用下向上运动，并从顶部离开提升管。所有粒子的直径与长度均相同。

3）主要数学模型

将气相场作为连续相，采用欧拉方法进行建模；将细长颗粒作为离散相，采用拉格朗日方法进行跟踪处理。

描述流化床中气相流场的数学模型包括：连续性方程、动量守恒方程，此外还需附加k－ε双方程湍流模型。

对于细长颗粒固相场的计算，为避免过大的计算量，以一定量的取样细长颗粒代替数目庞大的真实细长颗粒，通过跟踪计算每一个细长颗粒求解离散场。主要计算过程如下：首先将气相场划分为若干个网格，而将每一个细长颗粒分成若干等分，每分段细长颗粒近似为球形颗粒，分别判断每分段细长颗粒处于哪个气相场网格，并在相应气场网格内对每分段细长颗粒进行受力分析；然后对若干等分细长颗粒所受分力求矢量和，得到细长颗粒所受合力，并根据力矩公式求细长颗粒所受力矩；最后根据细长颗粒所受合力及力矩求细长颗粒在循环流化床内的运动。

其主要相关数学方程为：

（1）对于单个细长颗粒，平动方程为

图8－18　循环流化床结构示意图

式中，f为细长颗粒受到的流体力；f为每分段细长颗粒受到的流体力；s　··为细长颗粒的加速i度；m为细长颗粒的质量；g为重力加速度。

（2）对于单个细长颗粒，转动方程为

式中，M为细长颗粒受到的流体力矩；

为颗粒角加速度分量；Mi，Mj，Mk为力矩分量；Ji，Jj，Jk为颗粒对随体坐标系坐标轴的转动惯量；ωi，ωj，ωk为颗粒角速度分量。

（3）为避免坐标系变换过程中出现奇点，定义一组四元数：

式中，θ，Ψ，φ为描述颗粒运动姿态的欧拉角。这组四元数与随体坐标系的角速度关系为

（4）考虑到颗粒间碰撞，应采用两套网格，一套网格用于前面的受力分析，另一套网格则用来考虑颗粒间碰撞，并且后一套网格的单位网格尺寸明显大于用于受力分析的网格。对于Nabu模型，颗粒的扫掠体积是确定球形颗粒碰撞概率的重要因素之一。对于细长颗粒，由于投影面积与姿态有关，因此碰撞概率模型考虑了姿态的影响。在此基础上，对Nabu模型作适当修正，得到颗粒i和同一网格内其他所有颗粒的碰撞概率为

式中，n为真实颗粒数；N为取样颗粒数；Di，Dj分别为颗粒i和j的直径；θi为章动角；Gij为颗粒i和j的相对速度；Δt为时间步长。

在颗粒i总碰撞概率Ci＜1时，利用随机数R（0＜R＜1）选取网格内任一颗粒j（j＝int［RN］＋1），如果满足（R＞j/N－Cij）则发生碰撞，根据动量守恒定律获得颗粒i和j碰撞后的速度和角速度。

颗粒碰撞三维模型为：

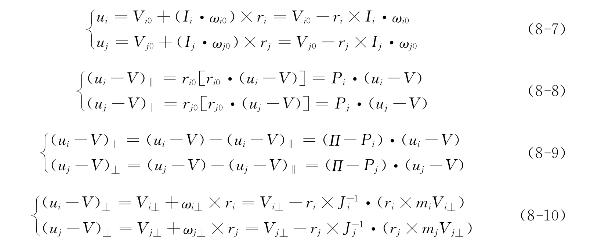
式中，ui，uj为颗粒碰撞前碰点速度；Vi0，Vj0为颗粒碰撞前质心速度；Ii、Ij为坐标转换余弦矩阵；ωi0，ωj0为碰撞前颗粒在随体坐标系中的角速度；ri，rj为碰点到颗粒质心的位置矢量；V为碰点最大压缩形变时的速度；ri0，rj0分别为ri，rj的单位矢量；Pi，Pj分别为ri0，rj0的并矢张量；qi，qj为冲量；e为恢复系数；Vi，Vj为碰撞后颗粒在随体坐标系中的质心速度；ωi，ωj为碰撞后颗粒在随体坐标系中的角速度；Π为定坐标系中的单位张量；Vi⊥，Vj⊥为颗粒在ri0，rj0垂直方向的速度变化；J′i，J″j为颗粒在随体坐标系中的转动惯量；Ji，Jj为颗粒在定坐标系中的转动惯量。

细长颗粒与壁面的处理采用镜面碰撞边界条件，气固两相间的相互作用采用单向耦合方式。

4）数值模拟结果与分析

图8－19（a）和（b）分别为通过数值模拟所获得的提升管内的气相场和细长颗粒流化运动的离散颗粒场。从图8－19（b）可见，由于提升管上部区域流化风速小于下部区域，造成上部区域细长颗粒的浓度明显大于下部区域的浓度，壁面附近区域的颗粒浓度小于中心区域的浓度，贴近壁面区域的细长颗粒似乎具有竖直姿态的取向性。相关规律还有待于进一步深入探讨和研究。

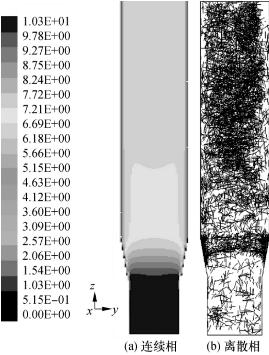
图8－19　提升管中细长颗粒流化运动的模拟结果

8.7　丝状柔性颗粒流化特性的数值模拟

1）数值模拟研究背景

一些具有柔软、易绕曲变形特征的丝状柔性颗粒，如烟丝、茶叶、纤维、牧草等，其流化运动特性与球形颗粒存在很大区别，如果将其简化成球形颗粒处理，势必存在较大误差。由于丝状柔性颗粒受力描述的复杂性，其流化特性的数值模拟一直是计算机数值模拟的难点。近年来，随着计算机计算能力的提高和数值模拟水平的发展，已有研究者开始尝试对丝状柔性颗粒的流化运动进行建模并进行数值计算，希望能够在现有条件下最大限度地真实反映丝状柔性颗粒的运动特性。尽管如此，丝状柔性颗粒多相流动的理论研究和数值模拟还均处于初级阶段。

图8－20　干燥烟丝的气流床装置

1—风机；2—料斗；3—进料口；4—提升管；5—旋风分离器；6—出料口；7—风管

2）所模拟的物理模型

以烟草加工中烟丝在气流床中的流化干燥过程为数值模拟对象。空气由床底部送入床层，柔性烟丝从右侧料斗加入床内，在气流携带作用下向上快速运动并从床顶部离开（图8－20）。

3）所采用的模拟方法和主要数学模型

根据丝状柔性颗粒在气流床中的流化特性，建模时将气相场作为连续相，采用欧拉方法进行处理；将丝状柔性颗粒作为离散相，采用拉格朗日方法进行跟踪处理。

描述气流床中气相流场的数学模型主要包括连续性方程、动量守恒方程等。

为了所建立的数学模型能够尽可能准确地表达丝状柔性颗粒的运动特性，采用一种丝状柔性颗粒的链式模型。在杆状颗粒的基础上，运用多刚体动力学理论，结合离散元方法的基本原理，将颗粒沿长度方向离散成若干段，段与段之间采用铰约束连接限制颗粒段之间的相对运动（图8－21）。通过颗粒段与段之间的运动相互耦合，反映柔性颗粒独特的动

力学效应，分段数目的多少取决于所模拟颗粒的柔性。此外，采用基于冲量定理的方法来处理颗粒间的相互作用。主要数学模型如下：

图8－21　丝状柔性颗粒的链式模型

（1）颗粒运动方程

如图8－21所示，将每一个颗粒沿其长度方向均匀离散成N段，则每个颗粒可看作由N个刚体构成的多刚体系统。首先在颗粒系统运动的平面定义一个惯性基e＝（x，y）T，对于颗粒段i，过其质心Ci建立其连体基ei＝（xi，yi）T，其位置和取向可以表示为

这N个列阵组集构成了描述该颗粒多刚体系统的笛卡尔坐标列阵，记为q：

由于颗粒段间存在铰，它限制了颗粒段之间的相对运动，这样对于某铰i＋1连接的一对邻接刚体颗粒段i和颗粒段i＋1，其中一个颗粒段的运动将部分地决定另一个颗粒段的运动。换言之，一般情况下，描述颗粒系统位形的笛卡尔坐标并不完全独立，在运动过程中它们之间存在某种关系。这些关系的解析表达式称为约束方程。因此描述每个颗粒对应的多刚体系统有个独立的完整约束，该约束方程组可表示为

Φ（q，t）＝0　　　（8－17）

结合第一类拉格朗日方程，采用引入的广义坐标矢量q，可得到多刚体系统的动力学方程为

式中，T为系统动能，V为系统势能，Q为系统广义力，包括常规作用力，如流体力和重力以及碰撞冲击力和摩擦力等。

（2）颗粒所受到的流体作用力

流体对颗粒的作用力即为流体力。当颗粒周围气流与颗粒间存在相对运动时，气流对颗粒产生力的作用：当气流速度大于颗粒运动速度时，气流对颗粒产生曳力；当颗粒运动速度高于气流流速时，颗粒受到运动阻力。

图8－22　二维细长柔性丝状颗粒的流体力分析

该模型忽略流体间的相互作用力，仅考虑流体对颗粒的作用力。流体对颗粒的作用力具体表现在流体对各个颗粒段的曳力作用。如图8－22所示，将颗粒沿其长度方向均匀离散成段（长度为l，宽度为d），假设颗粒段均质，力作用于颗粒段质心。将气相场划分为若干个网格，判断每一个离散颗粒的颗粒段所处的气相场网格，在相应气相场网格内对颗粒段进行曳力分析如下：

式中，FDi为颗粒段i所受流体曳力；ugi为颗粒段i所处气相场的速度；A，ρ和usi分别为颗粒段i的截面积、密度和速度；CD为细长颗粒的曳力系数，对于非球形颗粒的曳力系数按下式计算：

CD＝CDSPβ　　　（8－20）

式中，CDSP是基于体积的“当量”球形颗粒的曳力系数，β为非球形修正系数，其值见表8－1。

表8－1　颗粒非球形修正系数

球形颗粒的曳力系数采用Dalla　Valle推导的关系式：

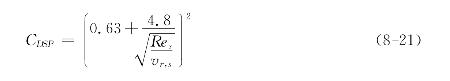
式中，雷诺数表示流体项的运动粘度，下标g表示流体相，下标s表示颗粒相，vr，s表示颗粒终端修正速度

式中；当αg≤0.85时，；当αg＞0.85时

，αg为流体相的容积份额。

颗粒与流体之间的交换系数为

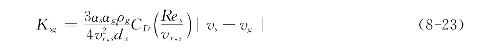
式中，αs为颗粒相的容积份额。

以流体曳力联合重力求得各颗粒段所受合力，其牛顿运动力学方程为

式中，a为颗粒段的加速度，m为颗粒段的质量，g为重力加速度。由于是根据颗粒段质心判断所处网格，而同一个网格中流场均匀，因此颗粒段沿长度方向受力均匀，且曳力作用于颗粒段质心，从而在重力和曳力作用下，颗粒段不发生转动。首先计算重力和曳力作用下各颗粒段的状态，然后考虑颗粒的碰撞，运用含铰摩擦的多刚体系统的碰撞动力学方程求解颗粒最终状态。

（3）计算颗粒碰撞的数学模型

如图8－23所示，设两颗粒在某时刻发生碰撞，具体表现为颗粒段i和颗粒段j发生碰撞，碰撞过程中仍假设系统的位形保持不变，冲击力以外的广义力忽略不计。对于碰撞接触点P，开始碰撞接触的瞬间在P点建立惯性直角坐标系（x，y），其中y为接触点处切平面的单位法向量并指向颗粒段i，于是运用基于冲量的颗粒段二维碰撞模型求解颗粒段碰撞后的状态。

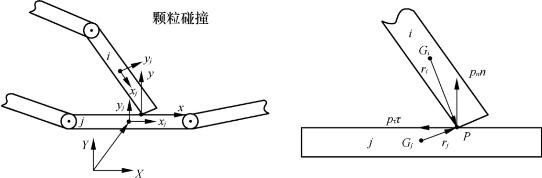
图8－23　基于冲量的杆状颗粒段二维碰撞模型

颗粒段i在碰撞点的碰撞前后的速度根据科氏加速度定理有

式中，vi为碰撞前颗粒段i在碰撞点P的线速度，由碰撞前颗粒段质心的线速度ui和角速度ωi与颗粒段质心到碰撞点的位置矢量ri的叉积两部分组成；ri在碰撞过程中不会改变，因为假设颗粒段在碰撞过程中不发生位置的变化；v′i，u′i和ω′i为对应的碰撞后各参数。

颗粒段质心线速度与角速度变化遵守冲量定理

式中，pn为碰撞点的法向冲量，Ii为颗粒段i相对质心的转动惯量。由式（8－25）—（8－28）可得

式中，n为碰撞点的法向单位矢量，v′i和pn是未知量。将后面已知部分化简为一常量矢量ci，类似地可得颗粒段j的简写方程式

颗粒段j的n与颗粒段i的相反，即－n。

利用vi，vj的切向相对速度vn，可以判断是否发生碰撞，如果｜vn｜＜0，意味着发生碰撞；如果｜vn｜＝0，意味着发生接触；如果｜vn｜＞0，意味着发生分离。vn的定义如下：

联立式（8－29）—（8－31）可得碰撞后的切向相对速度v′n

如果有n个碰撞点，这个方程可扩展为

为了计算冲量pn，定义一个恢复因数e，即碰撞前后相对速度的比，且该常数与碰撞物体的材料性质有关，与物体的形状、大小与碰撞前的速度无关。从而得到这个重要公式为

它表明：如果发生碰撞（pn＜＞0），那么方程就变为

联立以上式（8.34）—（8.35）即可得到颗粒段碰撞产生的法向冲量pn。切向冲量（摩擦力方向）仍可应用冲量方程，仅后面的判断方法不同。如果两个颗粒段接触并滑行，摩擦力会一直作用于滑行点上；同样地，如果发生碰撞，法向冲量与切向冲量（摩擦冲量）也同时工作，描述摩擦产生的冲量为摩擦冲量。如果摩擦力做功，相切的摩擦冲量将要运作，τ是单位法向矢量，如图8－23所示。这种情况下，切向速度与冲量的关系可以写成类似于式（8－33）的形式

运用求解法向冲量的方法可同样求得切向冲量为pτ1。另外，在无摩擦的情况下，正接触力fn（t）在［t0，t1］段间持续地作用于颗粒段j，因此P点的正冲量为

现在假设在P点的速度在碰撞开始和期间始终不为0，则等量摩擦力fτ（t）持续地作用，P点的摩擦冲量为

式中，μd为动摩擦系数。

假设在P点碰撞前切向速度变成了0，则摩擦力顶多保持在静摩擦状态，实际摩擦冲量pτ被限制在

式中，μs为静摩擦系数。

判断动静摩擦：如果｜pτ1｜＜μs｜pn｜，则pτ＝pτ1；反之，则pτ＝pτ2。

更为常见的是一个颗粒的颗粒段i同时与多个颗粒发生碰撞。此时，只需将这多个颗粒中的每一个颗粒的发生碰撞的颗粒段均视为上述颗粒段j进行处理，分别计算多个颗粒段j与颗粒段i的碰撞受力，然后计算作用于颗粒段i的合冲量和合力矩，从而求解各个颗粒段的碰撞后状态，而整个颗粒的状态则可联合碰撞颗粒段之间的铰约束共同计算。

另外，关于颗粒与静止壁面之间的碰撞，基于以上颗粒之间的碰撞理论，可以将壁面视为一质量很大的“颗粒”j，其cj＝0，转动惯量为0，碰撞前速度、角速度均为0，碰撞后位置和速度也均不发生改变。发生改变的仅仅是与壁面碰撞的颗粒，同时由于壁面性质的差异，颗粒与壁面碰撞时所采用的摩擦系数、恢复系数与颗粒之间碰撞时所采用的相关系数有所差别，其余求解方法均同颗粒间碰撞模型。

（4）颗粒段与颗粒段之间的铰约束模型

所建立模型将颗粒离散为颗粒段，将每个颗粒段视为个体，对于颗粒段在流场中的受力和颗粒碰撞的处理方法在前文已经做了具体介绍。然而，离散的颗粒段的状态得到后，单个颗粒段如何影响其相邻颗粒段的状态以及整体个颗粒的状态？这将通过颗粒段之间的连接——铰约束的控制来实现。本小节将对颗粒段之间的铰约束连接进行阐述，主要考虑了不可拉伸约束和摩擦约束。

①不可拉伸约束

由于各颗粒段呈刚性，不能拉伸，则铰连接在一起后，虽然整体可呈现柔性特征，但整个颗粒也不能延伸，如图8－24所示，对于铰约束i＋1，由铰接处的约束力Xi＋1维持其长度方向的不可延伸性，该力只与铰接的两颗粒段的位置和方向有关，因而有

图8－24　相邻颗粒段的铰接

ri＋lpi＝ri＋1－lpi＋1　　（8－40）

式中，ri为颗粒段i的位置矢量。该约束方程限制了两相邻颗粒段共用一个铰约束，因此作用在该约束上的力Xi＋1通常为0。

②摩擦约束

颗粒段之间通过约束限制不会发生相对分离，但由于颗粒段与颗粒段之间的速度差异和不可拉伸约束的限制，颗粒段会发生围绕其铰约束转动的相对运动，从而整体呈现出颗粒的扰动状态，而颗粒段相对转动的过程牵涉到摩擦约束。

以颗粒段i和颗粒段j为例，二者接触，接触处的摩擦导致相邻颗粒段间的运动牵连，因此

式中，n为接触点的法向单位矢量，τ为接触点的切向单位矢量，如图8－24所示。颗粒段i和颗粒段j的速度差Δuij为

Δuij＝6ri－6rj＋ωi×Gi－ωj×Gj　　（8－42）

摩擦约束与颗粒的运动方程以及不可拉伸约束相结合，运用库伦摩擦定律，可以判断动静摩擦

此时，在该摩擦力作用下，颗粒段不发生相对运动。

图8－25　部分丝状柔性颗粒的运动状态

4）数值模拟结果与分析

通过跟踪模拟流化过程中的几个样本颗粒，可观察到丝状柔性颗粒的运动特征（图8－25）。由于在受到气流作用的同时还会受到与其他颗粒或管壁的碰撞作用，丝状柔性颗粒各段受力通常不均匀，从而使得颗粒各段发生相对运动。但由于颗粒段之间通过铰约束的作用而相互限制，段与段之间绕连接点做相对旋转运动，颗粒整体呈现类似柔体的变形运动，与实际纤维、烟丝等丝状柔性颗粒的运动状态近似。

图8－26显示了提升管内丝状柔性颗粒在不同时刻流化运动状态的数值模拟结果。从图中可见，随着流化的进行，提升管内颗粒数量逐渐增加，颗粒在床内的分布出现汇聚现象，特别是在近壁区域这种现象比较明显，这与实验结果取得一致。图8－27是用高速摄像机记录下的烟丝在提升管中流化运动的实验照片，从照片可以看见近壁区域处烟丝的团聚现象。

图8－26　丝状柔性颗粒在提升管内流化运动的数值模拟结果

图8－27　烟丝在提升管内流化运动的高速摄像照片

采用相同建模方法对烟丝在滚筒烘丝机中的运动进行了计算机数值模拟，获得如图8－28所示的数值模拟结果，滚筒沿顺时针方向旋转，烟丝在滚筒内与较高温度的筒壁接触并得以烘烤，同时，烟丝随滚筒的转动而被抄板带到高处后抛下，在抛洒过程中与滚筒中轴向流过的热风进行热质交换。

图8－28　丝状柔性颗粒在滚筒中运动过程的数值模拟结果

8.8　大型袋式除尘器内流场的调节与优化

1）数值模拟研究背景

目前煤粉锅炉的除尘装置主要以静电除尘器和袋式除尘器为主，其中，袋式除尘器具有除尘效率高的特点。图8－29是袋式除尘器内部结构示意图，含有粉煤灰的烟气从喇叭口进入除尘器，穿过气流分布板进入除尘室，经过悬挂在花板上的滤袋过滤，烟气穿过花板进入净气烟道，通过净气出口离开除尘器。决定袋式除尘器正常工作的重要条件之一，是保证滤袋区的风速均匀，其最高风速必须限制在一定范围内，否则将导致滤袋的磨损，缩短除尘器的使用寿命。目前一台大型袋式除尘器体积庞大，内部需要悬挂数千条滤袋（图8－30），设计时如何掌握滤袋区的风速分布并控制在合理范围内是一件较为困难的事，而计算机数值模拟技术为大型袋式除尘器内流场的调节与优化提供了非常有效的手段和工具。通常的调节方法是根据除尘器内流场分布的需要，通过改变喇叭口气流分布板的开孔率来进行调节（图8－31），为了获得最为理想的流场分布，往往需要采用对气流分布板进行分区，不同区域对应不同开孔率的方式来加以调节，通过计算机对多种方案进行比较，获得最佳分区和开孔方案。

图8－29　袋式除尘器内部结构示意图

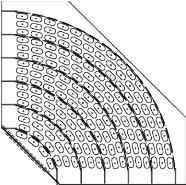
图8－30　滤袋区滤袋布置示意图

图8－31　气流分布板与开孔率变化

图8－32　所模拟的袋式除尘器结构示意图

2）所模拟的物理模型

图8－32是一个模拟大型袋式除尘器结构示意图，该除尘器原来为电除尘，现改为袋式除尘，需要通过数值模拟考察和调节其内部流场，以满足袋式除尘的需要。已知条件为袋式除尘器的结构尺寸、滤袋特性参数和入口烟气的物性条件，包括风速、烟气温度、含灰量等。

3）所采用的模拟方法和主要数学模型

建模时将气固两相分开，分别用欧拉方法建立气相场的数学模型并用拉格朗日方法建立离散颗粒场的数学模型，对离散颗粒场的模拟主要是为了能够将数值模拟结果制成动画，以直观、动态地了解除尘器内的烟气流动情况。

描述袋式除尘器内三维气相流场的主要数学模型包括连续性方程、动量守恒方程和k－ε双方程湍流模型，并利用FLUENT软件系统进行求解。

采用硬球模型描述离散颗粒场内颗粒的相互作用，运用蒙特卡洛方法扩大所模拟的颗粒量。

按照除尘器实际尺寸进行数值模拟，以提高数值模拟结果的准确性，采用6核双CPU工作站进行模拟计算。具体数学模型可参见本书第5、6章的内容。

4）数值模拟结果与分析

在对除尘器进行数值模拟之前，首先选定几个关键截面，用以评定其内部流场的分布特性。图8－33（a）中的迎风面V－V位于喇叭口出口和第一组滤袋区之间（贴近第一组滤袋区），可以反映喇叭口出口的高速烟气对滤袋迎风面的冲击情况，迎风面通常也是工程实际中滤袋最容易损坏的区域。如图8－33（b）所示，垂直截面A－A和B－B分别位于除尘器进气方向的轴对称位置和滤袋区的边沿，通过这两个垂直平面，能够反映除尘器内部纵向流场的特征。图8－33（a）中的水平截面H0－H0、H1－H1、H2－H2分别位于滤袋区的底部、中部、顶部，能够反映滤袋区的流场分布，该区域风速通常限定在2.5m/s以下。

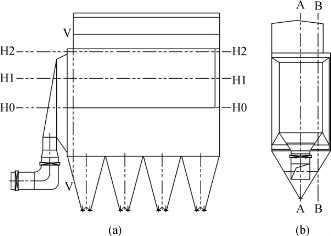
图8－33　除尘器内部流场分析选取截面

通过计算机数值模拟结果（图8－34）可以清楚地看到除尘器内流场的分布状况。由图可见，由于原有喇叭口较短，烟气进入喇叭口后不能及时转弯进入除尘室，而是流向除尘室的上部，造成除尘室上部的流速过高。从迎风面V－V的流场数据分布可见，在迎风面滤袋区（点划线所示区域）超速现象很严重，该区域最高流速达到了5m/s以上，大大超出了滤袋区的安全流速（一般限定在2.5m/s以内），这将极大地缩短滤袋的使用寿命。

对以上数值计算所发现的问题进行分析，发现导致除尘器内流场分布不均的主要原因是进入喇叭口的烟气在惯性的作用下不能及时拐弯进入除尘室内。为克服该问题，可在除尘器入口区域加装圆弧形导流板，将烟气合理地分配到除尘器内的整个空间，尽可能地使不同位置处的滤袋负荷一致，避免局部高风速、高负荷情况的发生。通过计算机对大量不同导流板方案的数值模拟结果进行比较分析和筛选，其中包括导流板位置、形状、块数、角度等，得到最终导流板方案。该方案为：在烟道拐角处添加两块圆弧形导流板并在喇叭口区域设置三块圆弧形导流板（图8－36），烟道拐角处的两块圆弧形导流板的作用主要是改善烟气拐弯向上后的流场分布，喇叭口区域的三块圆弧形导流板的作用是将气流合理地分配到除尘室，避免除尘器上部出现超速。

图8－34　原始方案下除尘器内部流场分布情况

从图8－35所示的流场分布图中可以看出，采用最终调节方案后，除尘器内流场分布情况得到了明显改善，从迎风面V－V能够看出，该迎风面滤袋区的流速基本降低到了2.5m/s以下，符合了工程设计的要求，将有效延长滤袋的使用寿命。

图8－35　最佳方案下除尘器内部流场分布情况

图8－36展示了采用最终调节方案后，除尘器内离散颗粒的分布状况。由图可见，离散颗粒在圆弧形导流板的作用下，从滤袋组的下部进入除尘器，有效地避免了对前排滤袋的冲刷作用。在除尘室内，颗粒分布很均匀，不同区域滤袋组的负荷基本一致，从而为提高除尘器的工作效率和延长滤袋的使用寿命提供了保证。

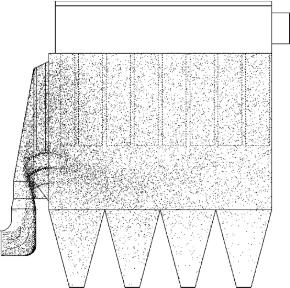
图8－36　最终方案下离散颗粒分布状态

8.9　循环流化床脱硫塔内气流分布的调节

图8－37　循环流化床脱硫塔

1）数值模拟研究背景

循环流化床脱硫塔是一种常用的干法脱硫装置。锅炉排出的烟气从脱硫塔底部进入（图8－37），经单个文丘里管或文丘里管束整合后进入床体，在文丘里管出口附近向床内喷入脱硫剂（如消石灰粉末）和适量的雾化水，与烟气一起在床内向上流动，在上升过程中脱硫剂与烟气中的硫化物接触并进行反应，从而将烟气中的硫化物脱除。脱硫后的烟气由床顶离开，通过旋风分离器实现气体与固体颗粒的分离，部分分离后的固体颗粒可再次从脱硫塔底部进入床内循环使用。

在实际实施过程中，由于烟道布置的原因，烟气通常在脱硫塔底部从某一水平侧面进入塔内，这样就造成塔内气流分布的不均匀，通常与烟气入口对面的一侧的气流流速较快，而与该侧相对的另一侧流速较慢，甚至会产生回流区。塔内流速的不均匀性会造成脱硫剂在塔内停留时间的差异，造成流速快的一侧脱硫反应时间不够，而流速慢的一侧反应时间不必要地过长，对整个脱硫塔的脱硫效率产生显著的影响，因此使脱硫塔内不同水平截面高度的流速尽可能地轴对称分布，是实现高效脱硫的重要前提。在工业实际中，由于脱硫装置十分庞大，给脱硫塔内流场的测量和调试均带来困难。尽管在实验室可进行缩小比例的模拟实验，但在工业放大过程中不可避免地会存在一定的偏差。

针对上述情况，采用计算机数值模拟可很好地解决这些问题，目前计算机的计算能力已经完全可以按实际脱硫塔的尺寸进行数值模拟计算，并达到令人满意的准确性。

首先，通过数值分析发现脱硫塔内存在流场不对称问题，进而根据存在的问题探讨在适当位置加装不同结构的导流板，通过在计算机上比较不同的导流板设想方案，最终筛选出最优导流板结构。上述方法是目前优化脱硫塔内流场分布情况的一种非常有效的方法，在这方面有大量成功案例，下面将根据典型案例予以介绍。

2）所模拟的物理模型

分别对采用单一文丘里管的循环流化床脱硫塔（图8－38）和采用文丘里管束的循环流化床脱硫塔（图8－39、8－40）进行模拟，烟气由脱硫塔底的一侧进入并由塔顶流出。为了便于观察脱硫塔内的气固两相动态流场，进入脱硫塔的烟气中设置一定浓度的离散粉体，粉体粒径取100μm。

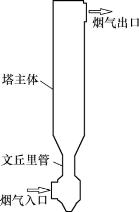
图8－38　采用单一文丘里管的循环流化床脱硫塔结构示意图

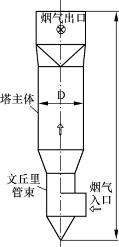
图8－39　采用文丘里管束的循环流化床脱硫塔结构示意图

图8－40　文丘里管束的结构示意图

3）所采用的模拟方法和主要数学模型

脱硫塔内的流动为烟气、粉煤灰和脱硫剂所构成的气固两相流动，建模时将气相和离散颗粒相分开处理，对气相场的建模采用欧拉方法，而对离散颗粒相的运动则采用拉格朗日方法加以描述。

描述脱硫塔内三维气相流场的数学模型包括连续性方程和动量守恒方程，另外，由于塔内烟气流速相对较高，因此还需附加k－ε双方程湍流模型。

固相的建模主要包括硬球模型和相关的离散颗粒运动方程，结合蒙特卡洛方法，以适应颗粒相计算量大的问题。具体数学模型可参见本书第5、6章的内容。

4）数值模拟结果与分析

图8－41给出的是通过数值模拟得到的采用单一文丘里管的循环流化床脱硫塔在没有调节措施的情况下塔内的气固两相流动分布情况。从图中可见，在塔底单侧进气的情况下，塔内的流场分布不能实现轴对称分布，与烟气入口对面一侧的气流流速较快，而与该侧相对的另一侧的流速较慢，并存在一个较大的回流区，该流场势必造成脱硫剂在塔内停留时间的显著差异，最终导致脱硫效率的降低。

图8－41　未采用调节措施情况下循环流化床脱硫塔内的气固两相流动分布情况

解决上述问题的途径是在脱硫塔底烟气转弯处加装导流板（图8－42），以使得入口烟气分批转弯。但所面临的问题是如何确定导流板的结构、块数、安装的空间位置等，这存在大量的组合与选择。为解决这一问题，计算机数值模拟可以发挥其优势，将需要加装的导流板设想方案设置成固体边界条件，通过模拟计算得到运行结果。经过对设想的不同导流板方案的比较和筛选，最终选定图8－42所示的三块导流板结构。采用该导流板方案，可使脱硫塔内的流场分布情况得到显著改善，由图8－43可以看出，流场基本可以达到轴对称分布，为高效脱硫建立了基础。

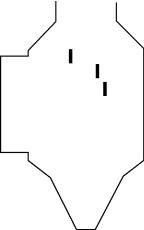
图8－42　经过数值模拟获得的最佳导流板结构

图8－43　采用调节措施后循环流化床脱硫塔内的气固两相流动分布情况

图8－44（a）给出的是通过计算机数值计算获得的在不加任何导流措施的情况下，采用文丘里管束的脱硫塔床层下部的气相流场。由图可以看出，塔内流速分布明显地偏向左侧，并有漩涡的存在。图8－45（a）给出的是与之对应的离散颗粒的流场分布情况。通过数值模拟对不同导流板方案进行比较和筛选，获得最终选定的导流板方案（图8－46）。采用该方案的气相流场和离散颗粒场分布情况分别如图8－44（b）和图8－45（b）所示，显而易见，流场分布情况得到显著改善并基本达到轴对称分布。

图8－44　调节前后循环流化床脱硫塔内的气相流场对比

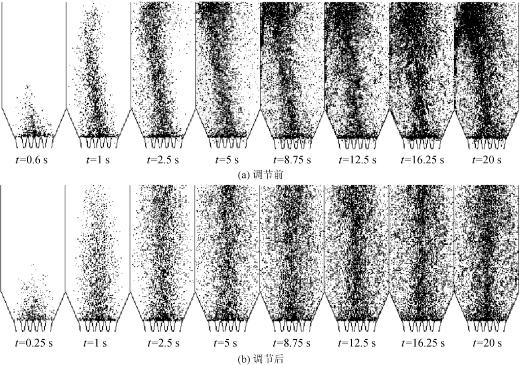
图8－45　调节前后循环流化床脱硫塔内离散颗粒随时间流动特征

图8－46　采用文丘里管束情况下循环流化床脱硫塔的导流板结构

目前，我国大部分火力电站由于场地和现场管道布置等条件的不同，循环流化床脱硫塔结构和运行参数的选取也存在差异，因此在设计导流板时，需要根据脱硫塔具体的几何尺寸和运行参数进行数值模拟计算，以确定合适的最佳结构。