与串联电路

观察与思考

在照明电路中，荧光灯电路的应用非常广泛。实际上荧光灯电路是最常见的RL串联电路，它是把镇流器（电感线圈）和灯管（电阻）串联起来，再接到交流电源上。荧光灯电路图和原理图如图7－3－1所示。把荧光灯接到交流电源上后，用万用表测得电源电压为220V，镇流器两端电压为190V，灯管两端电压为110V。

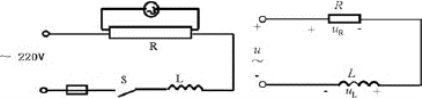
图7－3－1　荧光灯电路图和原理图

从测量结果看，交流串联电路中，总电压的有效值并不等于各电压有效值之和（220V≠190V＋110V），即U≠UL＋UR。那么在RL串联电路中，总电压的有效值与各分电压有效值之间到底满足怎样的关系呢？如果是RC串联电路或者是RLC串联电路呢？本节将学习RL、RC及RLC交流串联电路的分析方法、总电压与各分电压之间的关系、电路中的阻抗、功率及功率因数等相关知识与技能。

一、RL串联电路

电阻与电感串联组成的电路称为RL串联电路，如图7－3－2所示。RL串联电路包含了电阻、电感两个不同的电路参数，常见的线圈，如电动机、变压器的线圈就是RL串联电路。

1．总电压与各分电压之间的关系

交流电路的分析方法是以矢量图为工具，画矢量图时要先确定参考正弦量。因为串联电路中电流处处相等，所以分析RL串联电路要以电流作为参考正弦量。

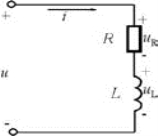
图7－3－2　RL串联电路

如图7－3－2所示，通过RL串联电路的电流为

i＝Imsinωt

则电阻两端的电压为

uR＝RImsinωt

电感两端的电压为

画出u、uR、uL及i的矢量图，如图7－3－3（a）所示。构成直角三角形，如图7－3－3（b）所示，我们称之为电压三角形。

根据基尔霍夫电压定律，电路总电压的瞬时值等于各个电压瞬时值之和，即

u＝uR＋uL

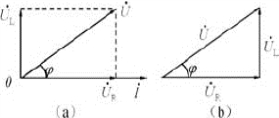
图7－3－3　RL串联电路矢量图和电压三角形

（a）电流与电压的矢量图；（b）电压三角形

由电压三角形可得到，总电压与各分电压的数量关系为

2．总电压与电流的相位差

从电压、电流的矢量图中可以得到，在RL串联电路中，总电压超前电流φ

职业相关知识：

通常情况下，将总电压超前电流的电路称为电感性电路，简称感性电路。

3．电路的阻抗

将UR＝RI、UL＝XLI代入总电压与各分电压的关系式中，则

上式整理后得

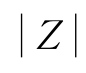称为电路的阻抗，单位是（欧姆）。它表示电阻和电感串联电路对交流电呈现的阻碍作用，阻抗的大小决定于电路参数（R、L）和电源频率f。

将电压三角形三条边同除以电流I，可以得到有阻抗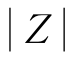电阻R和感抗XL组成的直角三角形，称为阻抗三角形，如图7－3－4所示。

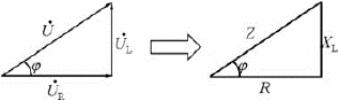
图7－3－4　阻抗三角形

阻抗三角形和电压三角形是相似三角形，阻抗三角形中与电阻R的夹角等于电压三角形中电压与电流的夹角φ，φ称为阻抗角，也是电压与电流的相位差。则

可见，φ的大小只与电路的参数R、L和电源频率有关，而与电压的大小无关。

4．电路的功率

将电压三角形的三边同乘以电流I，就可以得到由有功功率、无功功率和视在功率（总电压有效值与电流的乘积）组成的三角形——功率三角形，如图7－3－5所示。

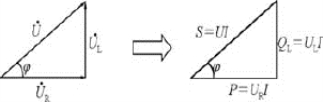
图7－3－5　功率三角形

（1）视在功率

我们把S称为交流电路的视在功率，视在功率表示电源提供的总功率（包括有功功率和无功功率），即交流电源的容量。视在功率用S表示，等于总电压有效值与总电流有效值的乘积，即

S＝UI

视在功率的单位为VA（伏安），常用单位还有kVA和MVA。

（2）有功功率

电路中只有电阻消耗功率，即有功功率，它等于电阻两端的电压与电路中电流的乘积，即

由于UR＝Ucosφ，所以

P＝UIcosφ＝Scosφ

（3）无功功率

电路中的电感不消耗能量，它与电源之间不停地进行能量转换，即无功功率，它等于电感两端电压与电路中电流的乘积，即

由于UL＝Usinφ，所以

QL＝UIsinφ＝Ssinφ

另外，从功率三角形还可以得到有功功率P、无功功率Q和视在功率S之间的关系，即

其中，阻抗角φ的大小也可以表示为

5．功率因数

在RL串联电路中，既有耗能元件电阻，又有储能元件电感。因此，电源提供的总功率一部分被电阻消耗（有功功率），一部分被电感与电源交换（无功功率）。这样就存在电源功率利用率的问题。为了反映功率的利用率，我们把有功功率与视在功率的比值称为功率因数，用λ表示，则

上式表明，当视在功率一定时，功率因数越大，用电设备的有功功率也越大，电源输出功率的利用率就越高。功率因数的大小由电路参数（R、L）和电源频率决定。

【例7－3－1】　可以通过测量实际电感线圈的电压和电流，进而求得线圈的电阻R和电感L。给线圈加直流电压12V，测得通过线圈的直流电流I＝2A；给线圈加交流工频220V电压，测得电流有效值为I＝22A，据此求出电阻R和电感L。

【解】　先求电阻R，直流作用下，根据欧姆定律可得

交流作用下，求的线圈的阻抗为

电感的感抗为

【例7－3－2】　某电动机接在220V工频交流电源上可获得14A电流，连接电动机电路中的功率表显示功率为2．5kW，试求该电动机的视在功率S、无功功率Q、功率因数角φ。

【解】　视在功率S＝UI＝220×14VA＝3080VA＝3．08kVA

由P＝UIcosφ＝Scosφ得

根据XL＝ωL＝2πfL求得电感L为

所以φ＝35．7°

Q＝UIsinφ＝3．08sin35．7°kvar＝1．8kvar

二、RC串联电路

电阻与电容串联的电路称为RC串联电路，如图7－3－6所示。在电子技术中，经常遇到阻容耦合放大器、RC振荡器、RC移相电路等，这些电路都是RC串联电路。

图7－3－6　RC串联电路

1．总电压与各分电压之间的关系

RC串联电路的分析方法同RL串联电路。

如图7－3－6所示，通过RC串联电路的电流为

i＝Imsinωt

则电阻两端的电压为

uR＝RImsinωt

电容两端的电压为

根据基尔霍夫电压定律，电路总电压的瞬时值等于各个电压瞬时值之和，即

u＝uR＋uC

画出u、uR、uC及i的矢量图，如图7－3－7所示，其电压三角形、阻抗三角形和功率三角形分别如图7－3－8（a）、（b）、（c）所示。

由电压三角形可得到，总电压与各分电压的数量关系

2．总电压与电流的相位差

从电压、电流的矢量图中可以得到，在RC串联电路中，总电压滞后电流φ，即

图7－3－7　矢量图

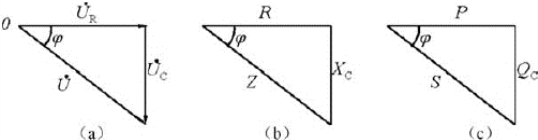
图7－3－8　RC串联电路的电压三角形、阻抗三角形、功率三角形

（a）电压三角形；（b）阻抗三角形；（c）功率三角形

职业相关知识：

通常情况下，将总电压滞后电流的电路称为电容性电路，简称容性电路。

3．电路的阻抗

电路的阻抗为

4．电路的功率

（1）视在功率

视在功率为

S＝UI

（2）有功功率

电路的有功功率为电阻消耗的功率，即

或

P＝UIcosφ＝Scosφ

（3）无功功率

或

QC＝UIsinφ＝Ssinφ

则有功功率P、无功功率Q和视在功率S之间的关系，即

【例7－3－3】　把一个阻值为30Ω的电阻和电容为80μF的电容器串联后接到交流电源上，电源电压u＝220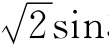314tV。求：（1）电容的容抗；（2）电路中电流的有效值；（3）电路中的有功功率P、无功功率Q和视在功率S；（4）端电压与电流之间的相位差。

【解】　由电压解析式u＝220314tV可得

电压的有效值U＝220V，角频率ω＝314rad／s

（1）电容的容抗为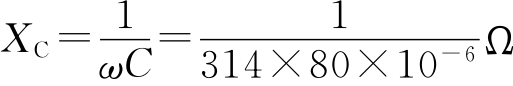≈40Ω

（2）电路的阻抗为

电路中的电流的有效值为A＝4．4A

（3）电路中的有功功率为

P＝RI2＝30×4．42　W＝580．8W

电路中的视在功率为S＝UI＝220×4．4VA＝968VA

电路中的无功功率为QC＝XCI2＝40×4．42＝774．4var

（4）端电压与电流之间的相位差为

三、RLC串联电路

电阻、电感、电容串联的电路称为RLC串联电路，如图7－3－9所示。RLC串联电路包含了三个不同的电路参数，在实际工作中常常遇到，如电子技术中的串联谐振电路和供电系统中的补偿电路。

1．总电压与各分电压之间的关系

RLC串联电路如图7－3－9所示，通过RLC串联电路的电流为

则电阻两端的电压为

i＝Imsinωt

uR＝RImsinωt

电感两端的电压为

电容两端的电压为

根据基尔霍夫电压定律，电路总电压的瞬时值等于各个电压瞬时值之和，即

u＝uR＋uL＋uC

画出u、uR、uL、uC及i的矢量图，如图7－3－10所示。

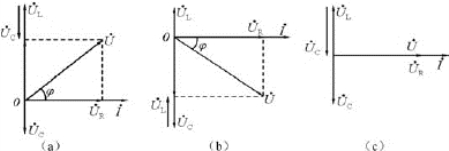
图7－3－10　RLC串联电路矢量图
（a）UL＞UC；（b）UL＜UC；（C）UL＝UC

由矢量图可得到，总电压与各分电压的数量关系为

2．总电压与电流的相位差

总电压与电流的相位差为

当UL＞UC时，φ＞0，电压超前电流；当UL＜UC时，φ＜0，电压滞后电流；当UL＝UC时，电压与电流同相位。

3．电路的阻抗

将UR＝RI、UL＝XLI、UC＝XCI代入总电压与各分电压之间的关系式中，则

上式整理后得

则

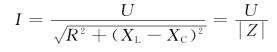
我们把X＝XL－XC称为电抗，它是电感与电容共同作用的结果；把称为交流电路的阻抗，它是电阻与电抗共同作用的结果。电阻与电抗的单位均为Ω（欧［姆］）。

同理，将电压三角形的三边同除以电流I，可以得到由阻抗、电阻R和电抗X组成的阻抗三角形，如图7－3－11所示。

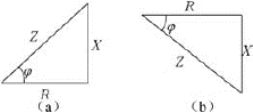
图7－3－11　RLC串联电路的阻抗三角形

由阻抗三角形可知，电路的阻抗角φ为

则阻抗角φ的大小取决于电路的参数R、L、C及电源频率f，电抗X的值决定着电路的性质。

1）当XL＞XC，即X＞0时，φ＝arctan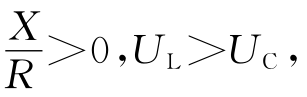 总电压超前总电流，电路呈感性；

2）当XL＜XC，即X＜0时，φ＝arctan 总电压滞后总电流，电路呈容性；

3）当XL＝XC，即X＝0时，φ＝arctan总电压与总电流同相，电路呈电阻性，我们称电路发生了谐振。

4．电路的功率

在RLC串联电路中，存在着有功功率P、无功功率QL和QC，它们分别为

P＝URI＝RI2＝UIcosφ

Q＝QL－QC＝（UL－UC）I＝（XL－XC）2I＝UIsinφ

S＝UI

在电阻、电感和电容串联电路中，流过电感和电容的是同一个电流，而电感两端电压uL和电容两端电压uC相位相反，感性无功功率QL和容性无功功率QC是可以互相补偿的，因此，电路中的无功功率为两者之差，即Q＝QL－QC。

如果将电压三角形的三边同乘以电流的有效值I，就可以得到由有功功率P、无功功率Q和视在功率S组成的功率三角形。则有

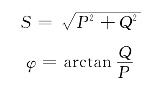
【例7－3－4】　已知某RLC串联电路中，电阻为30Ω，电感为127mH，电容为40μF，电路两端的交流电压u＝311sin314tV。求：（1）电路的阻抗值；（2）电流的有效值；（3）各元件两端电压的有效值；（4）电路的有功功率P、无功功率Q和视在功率S；（4）说明电路的性质。

【解】　由u＝311sin314tV可知，电源电压的有效值U＝220V，角频率ω＝314rad／s

（1）线圈的感抗XL＝ωL＝314×127×10－3Ω＝40Ω

电容的容抗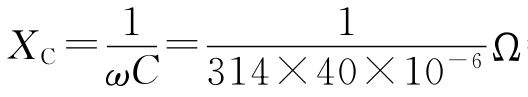＝80Ω

电路的阻抗＝50Ω

（2）电流的有效值＝4．4A

（3）各元件两端电压的有效值

UR＝RI＝30×4．4V＝132V

UL＝XLI＝40×4．4V＝176V

UC＝XCI＝80×4．4V＝352V

（4）电路的视在功率S、有功功率P、无功功率Q为

S＝UI＝220×4．4VA＝968VA

P＝RI2＝30×4．42　W＝580．8W

Q＝QL－QC＝（XL－XC）I2＝（40－80）×4．42var＝－774．4var

（5）电路的性质

因为XL＜XC，QL＜QC，即Q＜0，说明电路的性质为容性。

思考与练习

在RLC串联交流电路中，已知电源电压为100V，电阻R＝40Ω，XL＝40Ω，XC＝80Ω，则电路的阻抗＝_____，总电压与电流的相位差＝_____，电流的有效值I＝__________，电路的视在功率S＝_____，有功功率P＝_____，无功功率Q＝_____，该电路为_____性的电路。