§3.3 微分中值定理
作为函数和它的导函数之间相互联结的桥梁和纽带，微分中值定理赋予导数以鲜活的生命力。罗尔定理，Lagrange中值定理，柯西中值定理的证明思想质朴，环环相扣，辅助函数的引入更体现了数学思维的灵动美。
跟微分中值定理相关的题目一般都是证明题。下面我们按证题思路分述之。
一、妙用几何图形证题
从Rolle定理的证明，以及过渡到Lagrange中值定理所使用的辅助函数，都有明显的几何特征，而一旦将抽象的证明和具体形象的几何图形结合起来时，将会使我们对定理理解得更加深刻。
例1 设f（x）∈C［a，b］，且在（a，b）内可导。（以后我们将此两条件合并记为f∈C*［a，b］），且f（a）＝f（b），证明：
∃ξ1，ξ2∈（a，b），st f′（ξ1）>0，f′（ξ2）<0（f不为常数）。
证一 由于f（x）∈C［a，b］，且f（a）＝f（b），f不为常数，则在（a，b）内部必取得最大值或最小值之一，不妨设在ξ∈（a，b）处取得最大值f（ξ），于是
f（ξ）>f（a）＝f（b），在［a，ξ］上利用L-中值定理，∃ξ1∈（a，ξ），st
同理 ∃ξ2∈（ξ，b），st f′（ξ2）<0
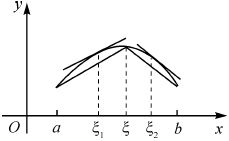
图3-1
证二 因f不恒为常数，知在（a，b）内，f′（x）不恒为0，不妨设∃ξ1，st f′（ξ1）>0。下证∃ξ2，st f′（ξ2）<0。
若不然，∀x∈（a，b），有f′（x）≥0，故f（x）在［a，b］上递增。从f′（ξ1）>0，∃δ1，st f（ξ1＋δ1）>f（ξ1）≥f（a），于是f（b）>f（a）矛盾。
故必∃ξ2，st f′（ξ2）<0，命题得证。
例2 假设f∈C*［a，b］，且f（x）非线性，证明∃ξ∈（a，b），st
证一 此题和例1是异曲同工的，正如L-中值定理和Rolle中值定理的联系一样。
为了去掉绝对值，先假设f（b）>f（a）时，构造辅助函数
那么F（x）不恒为0，F（x）∈C*［a，b］。不妨设∃x0∈（a，b），st F（x0）>0
在［a，x0］上运用L-中值定理，知∃ξ∈（a，x0），st
据此即有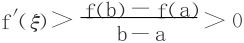 
若F（x0）<0，在［x0，b］上运用L-中值定理，一样得到所要求的ξ：
而当f（a）>f（b）情形，取g（x）＝－f（x），则依上述过程，∃ξ，st
综合两种情况，皆有
证二 依L-中值定理，∃x*∈（a，b），st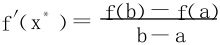
在［a，x*］和［x*，b］上分别应用L-中值定理，∃ξ1，ξ2，st
图3-2
由几何意义易知，
亦即ξ1，ξ2之中必有一个满足题目要求。
证三 （反证法）记
，若不然，∀x∈（a，b），有｜f′（x）｜≤k。因为f（x）非线性，∃ξ∈（a，b），st
故有
｜f（ξ）－f（a）｜<k（ξ－a），｜f（b）－f（ξ）｜<k（b－ξ）
所以
｜f（b）－f（a）｜<｜f（b）－f（ξ）｜＋｜f（ξ）－f（a）｜<k（b－a）
这与k的定义矛盾。
例3 设f在［a，b］连续，在（a，b）二阶可导，连结端点A，B的弦与曲线y＝f（x）相交于点C（c，f（c）），证明∃ξ，st f″（ξ）＝0。
（华中师范大学2003年）
这个题目本身就以几何形态的条件出发，而欲证明的f″（ξ）＝0无非提示出点M（ξ，f（ξ））是曲线的拐点。
图3-3
证一 若f″（x）>0，∀x∈（a，b）恒成立（为什么可以做这样的反证假定？）
则f（x）在［a，b］上严格凸，f（λ1x1＋λ2x2）≤λ1f（x1）＋λ2f（x2），则割线AB不可能与曲线y＝f（x）再相交于第三点C。
证二 在［a，c］上用L-中值定理，∃ξ1：
在［c，b］上用L-中值定理，∃ξ2：
在［ξ1，ξ2］上用Rolle中值定理于f′（x），就得∃ξ∈（ξ1，ξ2），st f″（ξ）＝0
二、构建辅助函数
从Rolle中值定理到L-中值定理，证明中使用了辅助函数
目的是将斜置的“弓形”转化为水平的“弓形”。依据不同的目的，构建恰当的辅助函数达成证明的目标，是数学中极为常用的手段，犹如几何学中添加辅助线。
例4 设f（x）在（a，b）内可导，且f（a＋0）＝f（b－0），则∃ξ∈（a，b），st f′（ξ）＝0。
（广义Rolle定理）
注 本题的开区间可以取无限区间。
证 情形1° 当（a，b）为有限开区间时，可以添加f在端点处的值使之成为在闭区间［a，b］上连续的函数，就可以应用Rolle中值定理。
情形2° （a，b）＝（－∞，＋∞）时，令x＝tant，
g（t）＝f（tant），则g（t）在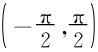
内连续，可导，符合情形1°的条件，
∃ 
，st g′（t0）＝f′（tant0）sec2t0＝0
由于sec2t0≠0，得出f′（tant0）＝0，取ξ＝tant0即行。
或证 设存在x0，f′（x0）>0，则一定存在x1，st f′（x1）<0，
（若不然，∀x∈R，有f′（x）>0，则f（x）↗。于是x>1时，有
f（－x）<f（0）<f（1）<f（x）；
则
，得出矛盾），由达布定理知结论成立。
情形3° （a，b）＝（a，＋∞）时，（单边无限的开区间），类似可以讨论
例5 假定f，g∈C*［a，b］，f（a）＝f（b）＝0，g（x）保号，试证：∃ξ∈（a，b），st
f′（ξ）g（ξ）＝g′（ξ）f（ξ）
证明 对
运用Rolle定理。
例6 设f（x），g（x）满足Cauchy中值定理条件，证明∃ξ∈（a，b），st
分析 欲证之式化为
f′（ξ）g（ξ）＋f（ξ）g′（ξ）＝f（a）g′（ξ）＋f′（ξ）g（b）
构造函数
F（x）＝f（x）g（x）－f（a）g（x）－f（x）g（b）
或
F（x）＝（f（x）－f（a））（g（x）－g（b））
证 欲证之式转化为 
或证 见上，F（x）≤0，若F（x）≡0，则
，∀ξ>0都满足。若F（x）不恒为0，则∃x0，F（x0）<0，由F（0）＝F（＋∞）＝0，存在0<x1<x0<x2，st F（x1）＝F（x2）介于F（x0）和F（0）＝0之间。在［x1，x2］上直接使用Rolle定理得证。
分析 欲证之式等价于ξf′（ξ）＋f（ξ）＝0。引入F（x）＝xf（x），显然F（0）＝0，相当于证∃ξ∈（0，1），st：F′（ξ）＝0，故只要在（0，1）中找两个点使得F（x）在该两个点函数值相等。
证明 
是F（x）＝xf（x）在区间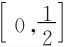
上的积分平均，依积分第一中值定理，∃
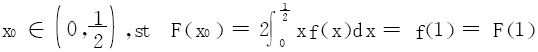，在［x0，1］上用Rolle定理。
例9 设f在［x，x＋h］上二次可微，τ∈［0，1］，则存在θ∈（0，1），使得
证明 不妨假定0<τ<1，设M（依赖于x，h，τ）满足
引入辅助函数（将上式中的τ置换成变量t）：
那么F（0）＝F（τ）＝F（1）＝0，又由f在［x，x＋h］上二阶可微，得知F（t）在（0，1］上亦二阶可微，连续用两次Rolle定理知存在θ∈（0，1），st F″（θ）＝0，此即f″（x＋θh）＝M
例10 设f在［a，b］上三阶可导，证明存在ξ∈（a，b），st
解法一 欲证之式改成
常数变易思路：上式左边的b改成变量x，引入
易见 F（a）＝G（a）＝0
F′（a）＝0
G′（x）＝3（x－a）2
G′（a）＝0
G″（x）＝6（x－a）
由Cauchy中值定理
解法二 令M满足
作辅助函数
则F（a）＝F（b）＝0，由Rolle定理∃x1∈（a，b），st F′（x1）＝0，整理得
再由Taylor公式，∃ξ∈（a，x1），st
比较（3），（4）二式即得知。
例11 设f（x）在有限区间（a，b）内可导但无界，证明f′（x）在（a，b）内也无界，其逆不真。
证一 反证法，逆命题不真的反例如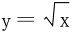
在（0，1）上。
证二 取点x0∈（a，b），∀M>0，∃x1∈（a，b），st
｜f（x1）｜≥max｛2｜f（x0）｜，2（b－a）M｝
在以x0，x1为端点的区间上运用L-中值定理，存在介于x0，x1之间的ξ，使得
故f′（x）在（a，b）上无界。
例12 设f∈C*［0，1］，且f（0）＝0，若∀x∈［0，1］，有｜f′（x）｜≤｜f（x）｜，证明f（x）≡0。
证明 ∀0<x<1，｜f（x）｜＝｜f′（ξ1）｜x≤｜f（ξ1）｜x≤…≤｜f（ξn）｜xn其中0<ξn<ξn－1<…<ξ1<x，令n→＋∞，得f（x）＝0，继而由f在x＝1点的连续性得知f（1）＝0，所以f在［0，1］上恒等于0
推广：设f在［0，∞）内可微，f（0）＝0，并且∃A>0，st｜f′（x）｜≤A｜f（x）｜恒成立。试证明f（x）≡0（中科院2003年）。
证法一 当
时，
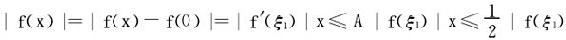
依次类推得
在
上，f（x）连续，故必有界，于是令n→∞，知
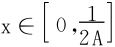时，f（x）≡0。
证法二 令
，对｜f（x0）｜使用上述技巧
∃η∈（0，x0），
，矛盾，或直接推得M＝0。
证法三 反证法，若∃x0>0，st f（x0）≠0，不妨设f（x0）>0，记x1＝i nf｛x｜（x，x0）上f（x）>0｝，显然f（x1）＝0。在（x1，x0）内定义，g（x）＝ln f（x），则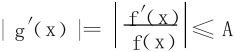
，故g（x）在有限区间（x1，x0）上有界，但由于
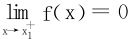，应有
，矛盾。
注 逆否命题：设f在［a，b］连续，在（a，b）可导，f（a）＝0，f（x）>0（a<x<b），则不存在常数M>0，使∀a<x<b有
。
例13 设f，g在R内有定义，f（x）二阶可导，且满足
f″（x）＋f′（x）g（x）－f（x）＝0
如果f（a）＝f（b）＝0，求证在［a，b］上，f（x）＝0
证明 题设对于函数g（x）的限定较模糊，若g（x）可以任取，则令g（x）≡0，原题中条件简化为f″（x）－f（x）＝0，其通解为f（x）＝C1ex＋C2e－x。
利用f（a）＝f（b）＝0，得出待定系数C1＝C2＝0，假若g（x）是一个特定的函数，设法令f′（ξ）g（ξ）项消失。
反证法，若∃x0∈（a，b），st f（x0）≠0，不妨设f（x0）>0，那么f在（a，b）内有最大值点ξ，于是f′（ξ）＝0，代入条件式知f″（ξ）＝f（ξ）>0。这说明f（x）在ξ处只能是最小值（极小值），矛盾。
例14 设f在（0，a］上可导，且
存在且有限，试证f在区间［0，a］上一致连续。
分析 归结为证明
存在即可以了。利用极限存在的Cauchy收敛准则和Cauchy微分中值定理来证：∀x，y∈（0，a］，∃介于x，y之间的ξ，st
利用
在0附近的局部有界性及在（0，ε2）内，
充分小即可。
习题3.3
1．f（x）在［a，b］连续，f（a）＝f（b）＝0；f在［a，b）内可导，且f′＋（a）>0；f（x）在（a，b）内二阶可微，证明存在C∈（a，b），使得f″（c）<0。
思路分析：f（a）＝0，f′＋（a）>0，则∃x0∈（a，b），st：f（x0）>0，在［a，x0］，［x0，b］上分别使用L-中值定理，∃ξ1∈（a，x0），f′（ξ1）>0，∃ξ2∈（x0，b），f′（ξ2）<0，在［ξ1，ξ2］上再一次对f′（x）使用L-中值定理，即得。或反证法f″（x）在（a，b）上非负，则f（x）为下凸函数，∀x∈（a，b）有f（x）≤f（a）＝f（b）＝0和f′＋（a）>0，矛盾。
2．设f（x）二阶可导，f″（c）≠0，试证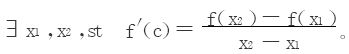
3．设f∈C′（R），f（a）＝f（b）＝0，f′（a）<0，f′（b）<0，证明至少存在两点ξ1，ξ2，st.f′（ξ1）＝f′（ξ2）＝0。
4．设f（x）∈C*［0，1］，f′（x）>0（0<x<1），f（0）＝0。证明：存在λ，μ∈（0，1），λ＋μ＝1，满足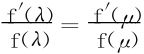
。
（华中理工1998年）
5．设f（x）∈C*［0，1］，且满足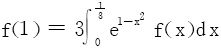
，证明存在ξ∈（0，1），使得f′（ξ）＝2ξf（ξ）。
（2001年数学（四））
6．设f（x）∈C*［a，b］，且f（a）＝f（b）＝1，证∃ξ，η∈（a，b），st eη－ξ（f（η）＋f′（η））＝1。
（1998年数学（四））
（1）
（2）∀λ∈R，∃ξ∈（0，η），st f′（ξ）－λ（f（ξ）－ξ）＝1。
（1999年数学（三））
8．设f∈C*［a，b］且f′（x）≠0。试证∃ξ，η∈（a，b），st
（1998年数学（三））
9．设函数f在点a的某个邻域内具有二阶导数。证明：对充分小的h，存在θ，0<θ<1，使得
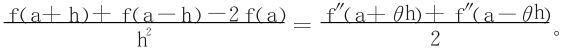
10．已知f在［0，1］上三阶可导，f（0）＝－1，f（1）＝0，f′（0）＝0。试证至少存在一点ξ∈（0，1），使得
（浙江省高等数学竞赛2004年）
11．设f在R上可导，∀x≠y，有
，求证
f（x）＝ax2＋bx＋c。
12．设函数f（x）处处有连续的二阶导数，试证：
13．设f（x）在［a，b］连续，在（a，b）有二阶导数，证明，∃ξ∈（a，b），st
。
（南开大学1982年）
14．函数f（x）在［0，x］上的拉格朗日公式为f（x）－f（0）＝f′（θx）x，其中0<θ<1，对f（x）＝arctanx，求x→0＋时θ的极限值。
（武汉大学2000年）
15．设f在［0，1］可微，f（0）＝0，f（1）＝1，λi∈（0，1）且
，证明：存在一组互不相等的x1，x2，…，xn，使得
（中国科技大学；浙江省数学竞赛03年）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
